冲激函数δ(t)及其导数的微分方程求解

方 飞， 肖立文

(内江师范学院 物理与电子信息工程学院， 四川 内江 641100)

0 引言

《信号与系统》是电子信息类专业的核心课程，该课程理论性强、过于抽象,学生学起来普遍有畏难情绪[1].单位冲激响应是分析线性时不变(linear and time invariant，LTI)系统的稳定性、因果性等特性的重要方法[2].教学中发现，阻碍学生学习兴趣的常常是某些知识点理解不到位，而冲激函数δ(t)(也称奇异函数)及其响应就加重了学生的理解难度.

当前对《信号与系统》课程的研究主要集中教学模式及教学方法改革[3-6]和课程思政[7-10]等方面.杜世民等[2]利用奇异函数平衡法、等效初始条件法、线性分析法分析了冲激响应的求解算法；张国强等[11]对单位冲激信号的引入方法进行了对比；许梅等[12]对单位冲激信号的性质进行了研究.已有的研究都未对冲激函数的导数及高阶导数性质进行分析，没有对微分方程中出现冲激函数的高阶导数如何求解展开研究，而拉氏变换求解算法中又经常用到.针对此问题，本文对微分方程中出现冲激函数的高阶导数时如何采取经典方法进行求解开展研究.

1 微分方程经典求解算法

二阶常系数微分方程如下：

y″(t)+5y′(t)+6y(t)=f′(t)+f(t).

(1)

假定系统初始值为零，即

y′(0-)=0,y(0-)=0，

(i)当f(t)=u(t)，求系统的全响应；

(ii)当f(t)=δ(t)时，求系统的全响应.

依据线性微分方程求解方法，得到微分方程的特征方程为：

α2+5α+6=0，

(2)

求得特征根为α1=-2，α2=-3，齐次解为：yh(t)=C1e-2t+C2e-3t.

由于δ(t)、δ′(t)及其高阶导数只在0时刻起作用，因此对于(i)的求解，式(1)的右边变为δ(t)+u(t)，依据冲激函数匹配方法，左边y″(t)将出现δ(t)，在0-到0+时刻，y′(t)将发生跃变，y′(0+)=y′(0-)+1=1.

微分方程的特解为：

yp(t)=1/6.

微分方程的全解可表示为：

代入初始值：

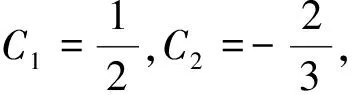
(3)

对于(ii)的求解中，右边激励变成3δ′(t)+2δ(t)，对于δ(t)引起的响应可以按照(i)所求方法进行求解.然而当激励为δ′(t)时，依据冲激函数匹配方法，左边y″(t)将出现δ′(t)项，y′(t)将出现δ(t).依据δ(t)的性质，在0-到0+时刻，y(t)将发生跃变.此时将产生如下问题：

(1)当y″(t)中包含δ′(t)项时，也可能包括δ(t)项，此时如何确定系数；

(2)y″(t)中δ′(t)项从0-到0+是否会引起y(t)发生跃变.

这是在求解含δ′(t)的微分方程时很难理解的地方，也是包含δ(t)导数及高阶导数的微分方程在求解过程中面临的问题.

2 拉氏变换求解算法

二阶常系数微分方程如下：

y″(t)+5y′(t)+6y(t)=f′(t)+f(t).

(4)

依据拉氏变换求解方法，对方程两边进行拉普拉斯(Laplace)变换，当初始条件为0时，得到方程的拉氏变换：

s2Y(s)+5sY(s)+6Y(s)=sF(s)+F(s)，

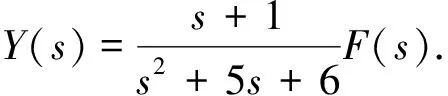
(5)

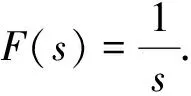
(6)

是由激励f′(t)=δ(t)引起的响应，依据拉氏反变换，可以求得在该激励下的响应为

y1(t)=(e-2t-e-3t)u(t)；

由激励f(t)=u(t)引起的响应，依据拉氏反变换，可以求得在该激励下的响应为

全解为：

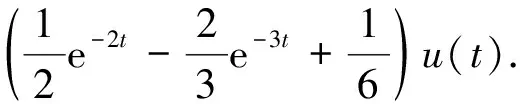
(7)

(ii)当f(t)=δ(t)时，F(s)=1，

(8)

是由激励f(t)=δ(t)引起的响应，依据拉氏反变换，可以求得在该激励下的响应为

y1(t)=(e-2t-e-3t)u(t)；

是由激励f(t)=δ′(t)引起的响应，依据拉氏反变换，可以求得在该激励下的响应为

y2(t)=(-2e-2t+3e-3t)u(t).

全解为：

y(t)=y1(t)+y2(t)=(-e-2t+2e-3t)u(t).

(9)

3 含δ(t)及其导数方程的求解

依据LTI系统的线性特性，松驰条件下(初始条件为0)的微分方程y″(t)+b0y′(t)+b1y(t)=f′(t)+f(t)可以分解为两部分：

y″(t)+b0y′(t)+b1y(t)=f1(t)+f2(t)，

其中f1(t)=f2′(t)，因此只考虑微分方程最简单的形式

y″(t)+b0y′(t)+b1y(t)=f(t)类型的微分方程.

3.1 激励为δ(t)的响应

定理1对于二阶线性常系微分方程，y″(t)+b0y′(t)+b1y(t)=mf(t)，若其特征方程的根为非重根，则该微分方向的冲激响应为：

y(t)=C1ea1+C2eα2，t≥0，

且C1，C2由如下方程确定：

(10)

其中，α1，α2是微分方程对应特征方程的特征根，m是激励δ(t)的系数.

证明：

先考虑一常见微分方程：

y″(t)+b0y′(t)+b1y(t)=mf(t).

假设其特征根为α1，α2,(α1≠α2).由特征根的计算表达，可知：

α1+α2=-b0，α1×α2=b1.

当输入激励为f(t)=δ(t)时，得到微分方程的拉氏变换为：

(11)

得出系统的响应为：

依据传统常系数微分方程的求解方法，得到该微分方程的特征方程为：

α2+b0α+b1=0，

求得特征根α1，α2,(α1≠α2).

微分方程的解可写成：

y(t)=C1eα1t+C2eα2t，t≥0.

输入为δ(t)时，左边y″(t)将出现δ(t)，在0-到0+时刻，y′(t)将发生跃变，

y′(0+)=y′(0-)+1=m.

代入初始值：

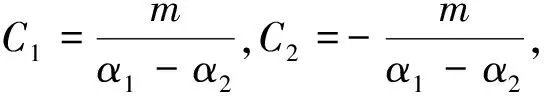
(12)

比较两种解法，可以发现，在输入为δ(t)时，由拉氏变换分式分解求得的k1，k2与采用传统微分方程求解得到的C1，C2相同.

将该结论应用于微分方程：

y″(t)+5y′(t)+6y(t)=3f(t)

的冲激响应求解.利用拉氏变换求解得到该微分方程的解为

y(t)=e-2t-e-3t,t≥0.

由式(2)的公式m=3，α1=-2，α2=-3，推导得出C1=k1=3，C2=k2=-3.测试结果表明定理的准确性.

3.2 激励为δ′(t)的响应

定理2对于二阶线性常系微分方程，

y″(t)+b0y′(t)+b1y(t)=mf(t)，

其激励为δ′(t)的响应为：

y(t)=C1eα1t+C2eα2t，t≥0，

且C1，C2由如下方程确定.

(13)

其中，α1，α2是微分方程对应特征方程的特征根，m是激励δ′(t)的系数.

证明：

依据LTI系统的线性特性，松驰条件下(初始条件为0)且不出现重根的二阶线性微分方程y″(t)+b0y′(t)+b1y(t)=mf(t)，假设α1，α2是微分方程对应特征方程的根.当输入激励为f(t)=δ′(t)时，F(s)=s，得到微分方程的拉氏变换为：

(14)

得出微分方程的解为：

(15)

而微分方程对应特征方程为

α2+b0α+b1=0，

求得特征为根为α1，α2.

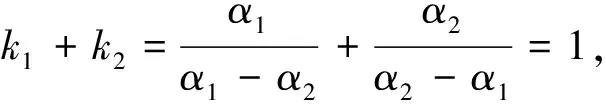
3.3 激励为δ′(t)的响应

定理3对于二阶线性常系微分方程，

y″(t)+b0y′(t)+b1y(t)=mf(t)，

其激励δ′(t)响应为：

y(t)=m(δ(t)+C1eα1t+C2eα2t)，t≥0，

且C1，C2由如下方程确定：

(16)

其中，α1，α2是微分方程对应特征方程的特征根，m是激励δ(t)的系数.

证明：

依据LTI系统的线性特性，松驰条件下(初始条件为0)且不出现重根的微分方程

y″(t)+b0y′(t)+b1y(t)=mf(t)，

假设α1，α2是微分方程对应特征方程的特征根.当输入激励为f(t)=δ″(t)时，F(s)=s2时，得到微分方程的拉氏变换为：

得出微分方程的解为：

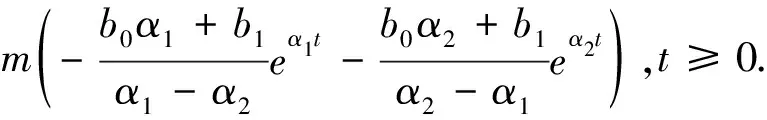
(18)

而微分方程对应特征方程为α2+b0α+b1=0，求得特征为根为α1，α2.使用经典求解方法的冲激函数匹配法，y(t)必然包含δ(t)，y″(t)包含mδ″(t)，但是难以确定δ″(t)对y′(t)及y(t)的影响，这也是经典求解算法存在的问题.通过分析发现：

正好是微分方程y′(t)的系数；

是y′(t)的系数.

验证：将该推论应用于微分方程

y″(t)+5y′(t)+6y(t)=f(t)，

其解为

y(t)=δ(t)+4e-2t-9e-3t，t≥0，

可以得出：

(19)

对于方程

y″(t)+3y′(t)+2y(t)=f(t)，

其解为

y(t)=δ(t)+e-t-4e-2t，t≥0，

可以得出

(20)

两个方程满足相同的条件，验证结论正确.

4 结论

经典的微分方程求解算法在求解含冲激函数δ(t)及其一阶、二阶导数甚至高阶导数时，无法解决在0-到0+时刻，冲激函数引起的初始状态变化情况.拉氏变换通过将微分方程变成线性方程，并通过将积分限设置为0-的方式来避免0-到0+时刻系统状态变化，简化了微分方程的求解过程.在实际系统分析中，尽量采用拉氏变换来求解实际电路微分方程.经典微分方程求解是傅里叶变换、拉氏变换以及Z变换算法的基础，学生必须掌握经典求解算法技巧与方法.本文提出的系统匹配方法只针对了二阶不重根的方法，包含δ(t)三阶导数及以上微分方程的匹配算法还需要进一步证明.