关联代数上的内导子

周斯名， 袁 鹤

(吉林师范大学 数学学院， 吉林 长春 130000)

0 引言

关于内导子、内导性的研究一直深受研究人员的关注，内导子在导子方面的相关研究起到非常重要的作用,内导子渗透在导子研究的诸多方面.文献[1]讨论了素环理想上内导子的交换性质；文献[2]讨论了素环理想上广义内导子的交换性；文献[3]得出了单位元交换环上全矩阵代数上导子为内导子的充分条件；文献[4]证明套代数上任何一个导子都是内导子；文献[5]证明三角代数上的Jordan导子是三角代数上的内导子；文献[6]证明关联代数上的传递映射是内导子当且仅当传递映射是平凡的；设F是特征不为2的域，M(n,F)为域上全体n×n阶矩阵构成的矩阵代数，α为Fn中非0列向量，令L(α)={A∈M(n,F)Aα=0}.文献[7]证明了L(α)的所有的Jordan导子都是内导子.上述文章均停留在内导子与其他映射的联系层面或相关映射的内导性问题方面，没有真正分析内导子的具体形式和内在性质.本文利用代数结合的方法研究算子理论，并在此基础上探究了关联代数上的内导子的具体表达形式，进而为其他结论的研究提供了关联代数上的内导子的具体表达形式，对于内导子的相关结论有重要意义.

广义导子是比导子更广泛的一类映射，广义导子相关结论的研究也受到许多学者的关注,并得到了一系列的结论，其中广义Jordan导子的相关结论在研究中有着广泛的应用.文献[8]证明了完全矩阵代数上的每一个广义Jordan导子是导子与广义内导子之和；文献[9]证明了三角代数上的每一个广义Jordan导子是导子与广义内导子之和；文献[10]证明了每个广义李导子是广义内导子和李导子之和；文献[11]证明了2-非挠的交换半环上的全矩阵代数Mn(R)上的每个广义Jordan导子都是广义内导子,进而它也是一个广义导子.本文受上述结论启发结合关联代数，证明了关联代数上的每一个广义Jordan导子都是导子与广义内导子之和.

1 预备知识

定义1.1设φ、φ为代数R上的可加映射,

(1)若对于任意的A,B∈R都有φ(AB)=φ(A)B+Aφ(B),则称φ为代数R上的导子.

(2)若对于任意的x∈R,如果存在a∈R, 使得φ(x)=[x,a]=xa-ax成立, 则称φ为代数R上的内导子.

(3)若对于任意的x∈R,有φ(x2)=φ(x)x+xφ(x),则称φ为代数R上的Jordan导子.

(4)若存在导子φ：R→R使得对于任意的A,B∈R,有φ(AB)=φ(A)B+Aφ(B),则称φ为代数R上的广义导子.

(5)若存在T,S∈R使得对于任意的x∈R,有φ(x)=Tx+xS,则称φ为代数R上的广义内导子.

(6)若存在Jordan导子φ：R→R使得对于任意的x∈R,有φ(x2)=φ(x)x+xφ(x),则称φ为代数R上的广义Jordan导子

关联代数的概念最早是Ward[16]引出，之后人们对关联代数上的映射进行了研究(参考文献[14-27]).

定义1.2若集合X中的二元关系≤满足以下两个条件：

(1)∀x∈X,有x≤x；

(2)∀x,y,z∈X,若有x≤y和y≤z,就有x≤z,

则称X是一个预序集，记作(X,≤).

定义1.3对于预序集X中的任意两个元素x、z,区间[x,z]定义为{y∈X|x≤y≤z}.若预序集X中的所有区间都是有限的，则称X是局部有限预序集.

定义1.4[13]设R是含单位元的交换环，(X,≤)是一个局部有限预序集，即≤满足自反性、传递性.对任意的x,y∈X,且x≤y,至多存在有限个元素z∈X,满足x≤z≤y,由此可在R上定义关于X的关联代数I(X,R):={f:X×X→R|f(x,y)=0,若x≤y不成立}.代数运算如下：

(f+g)(x,y)=f(x,y)+g(x,y),

(rf)(x,y)=rf(x,y),

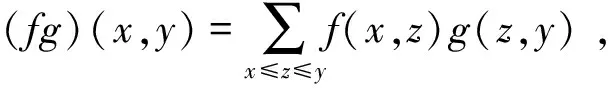
∀f,g∈I(X,R)，r∈R，x,y,z∈X.

乘积fg在函数论中被称为卷积.

引理1.1[13]δ满足δ(x,y)=δxy，x≤y，其中δxy∈{0，1}是Kronecker符号，则δ是关联代数I(X,R)中的单位元.

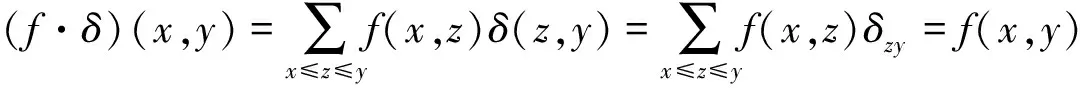
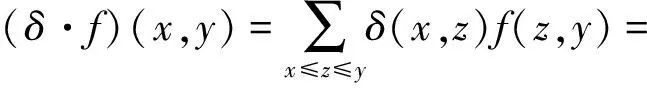
则δ是关联代数I(X,R)上的单位元.

对任意的x,y∈X,满足x≤y,则可定义关联代数I(X,R)上的基元exy,

对任意eij,ekl∈I(X,R),根据卷积定义eijekl=δjkeil,可以证明B：={exy|x≤y}构成I(X,R)上的一组线性基.

2 主要定理及证明

定理2.1设φ:I(X,R)→I(X,R)是一个R-线性算子，则φ是内导子当且仅当φ满足形式

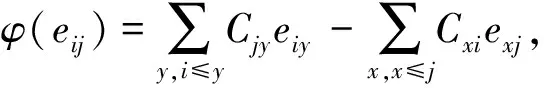
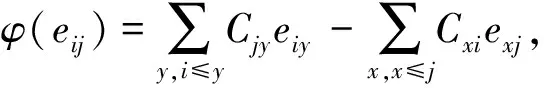
(1)对于φ(eii),根据卷积定义有

应在就业指导、就业能力提升等方面增加资金投入，加强这方面的软硬件实力，以确保大学生就业能力的提升。高校可与财政部门加强沟通，争取财政部门给予高校更多的资金支持，提高学校的硬件设施条件，改善大学生的学习环境，改善就业指导方面师资力量不足的情况。同时，应增加教师资源的投入，提高教师的福利待遇，充分调动教师在就业指导方面的积极性。

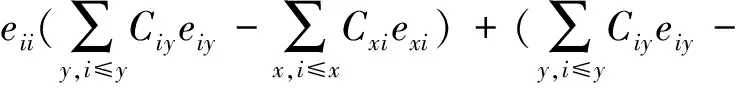
则可得φ(eii)是导子.

(2)对于φ(eij),根据卷积定义有

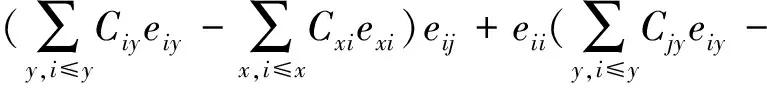
则φ(eij)是导子.

再证明满足①的φ为内导子，只需证明∀x∈I(X,R)存在a∈I(X,R),满足φ(x)=[x,a]=xa-ax.

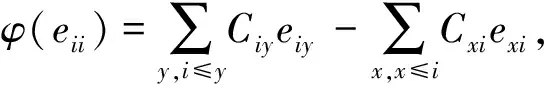
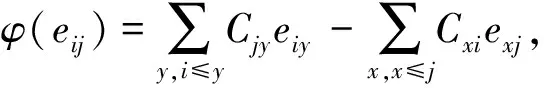
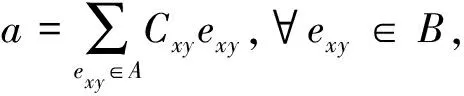
代入

φ(eij)=φ(eii)eij+eiiφ(eij)、φ(eij)=φ(eij)ejj+eijφ(ejj)及φ(eij)=φ(eiieijejj)=φ(eii)eij+eiiφ(eij)ejj+eijφ(ejj)

均成立.

引理2.1φ为代数R上的广义Jordan导子，对于任意a,b,c∈R,则有：

φ(ab+ba)=φ(a)b+aφ(b)+φ(b)a+bφ(a).

证明由φ：R→R是一个广义Jordan导子，则满足φ(x2)=φ(x)x+xφ(x),将x=a+b代入上式，有

φ((a+b)2)=φ(a+b)(a+b)+(a+b)φ(a+b),因此φ(a2+ab+ba+b2)=φ(a2)+φ(ab)+φ(ba)+φ(b2).比较这两个表达式有φ(ab+ba)=φ(a)b+aφ(b)+φ(b)a+bφ(a).

引理2.2[6]设D:I(X,R)→I(X,R)是一个Jordan导子.此时

对于所有eij∈Β,其中系数满足以下关系

引理2.3[14]设D:I(X,R)→I(X,R)是一个R-线性算子，则φ是导子当且仅当φ满足

其中系数eij∈Β满足如下关系式

定理2.2设(X,≤)是一个有限预序集，R是含单位元的交换环.设I(X,R)是定义在R上关于X的关联代数，则I(X,R)上的每个广义Jordan导子都是导子与广义内导子之和.

证明分两种情况进行证明.

(1)对于eii∈I(X,R),若φ：I(X,R)→I(X,R)是广义Jordan导子，则有φ(eii2)=φ(eii)eii+eiiφ(eii),其中φ：I(X,R)→I(X,R)是导子，则由φ(eii)、φ(eii)∈I(X,R),满足广义内导子φ(eii)=φ(eii)eii+eiiφ(eii),则φ为关联代数I(X,R)上的广义内导子.

3 结论

本文利用组合与线性代数的方法研究了关联代数上的内导子的具体表达形式，进而借助已有定理证明了关联代数上的每一个广义Jordan导子都是导子与广义内导子之和.