动密封用Ni基合金斜圈弹簧的变形行为及回弹力模拟
2022-09-05余煜玺张伟彬孙轶丛明辉朱建宋经远
余煜玺,张伟彬,孙轶,丛明辉,朱建,宋经远
1. 厦门大学 材料学院,厦门 361005 2. 中国航发沈阳发动机研究所,沈阳 110015
动密封结构广泛运用于航空航天器高温暴露部位(如飞行器的控制面及冲压发动机等)的间隙密封,以防止高温氧化热气流(约为800 ℃)进入结构内部,保证飞行器的安全性能。斜圈弹簧作为动密封结构的弹性元件,为动密封结构提供回弹性能,确保在热负荷和结构载荷作用下,当密封间隙打开时,能及时为动密封结构补偿变化间隙,提高动密封结构的密封性能,是影响动密封结构密封性能的一项重要因素,因此对斜圈弹簧变形行为及回弹力的研究显得尤为关键。
在目前的研究中,王建平等通过理论计算研究了斜圈弹簧的非线性刚度,对斜圈弹簧的非线性机制进行了一定解释,但模型复杂,计算难度较大;Kaoua等利用有限元方法模拟了在轴向载荷作用下双螺旋弹簧的变形行为,未对弹簧的径向载荷作用进行研究;颜燕琼和刘宏昭研究了斜圈弹簧的力学特性,但未对变形过程进行研究。在大部分研究中,对斜圈弹簧线圈轴向的偏移程度采用线圈与径向的夹角,即倾斜角定义,该定义方法的方程将倾斜角、线圈高和线圈宽三者设定为关联变量,无法对其进行单独讨论。而本文采用偏移量,即倾斜程度定义,这种定义方法的方程可将倾斜程度、线圈高及线圈宽作为单独变量,可更为全面地讨论各项结构参数对斜圈弹簧力学特性的影响。Inconel X-750作为一种时效强化的Ni基高温合金,具有良好的柔韧性、耐高温、耐氧化性能,是制备动密封用斜圈弹簧的理想候选材料。
综上,本文将以倾斜程度定义斜圈弹簧在轴向的偏移量,以Inconel X-750镍基合金作为候选材料进行模拟分析,以实验校验有限元模拟分析的可靠性,并讨论斜圈弹簧在径向载荷作用下的变形行为及结构参数、温度对斜圈弹簧回弹力的影响,从而实现斜圈弹簧的可设计性。
1 斜圈弹簧几何建模
1.1 斜圈弹簧作用与几何结构
动密封结构安装部位如图1(a)所示,可对发动机进气道的调节面板在运动时产生的间隙起到密封作用;图1(b)为动密封结构安装示意图,主要由陶瓷栅板和斜圈弹簧组成,而Inconel X-750镍基合金斜圈弹簧的主要作用是保证密封陶瓷栅板与密封表面紧密贴合及补偿间隙变化,但回弹力过大容易损坏密封接触面上的隔热涂层,加速结构破坏,因此斜圈弹簧回弹力的研究至关重要。

图1 动密封结构示意图Fig.1 Installation diagram of dynamic sealing structure
与普通螺旋弹簧不同,直线型斜圈弹簧在轴向上有一定的倾斜程度,且一般承受径向载荷,如图2(a)所示;斜圈弹簧在径向压缩的过程中,回弹力在较大的压缩范围内几乎保持恒定,如图2(b)所示。该恒定平台对斜圈弹簧回弹力设计有着至关重要的作用,能够保证其在较大的压缩量范围内保持设定值,防止在服役过程中压缩量偏大或偏小导致密封失效抑或破坏接触面的防热涂层。
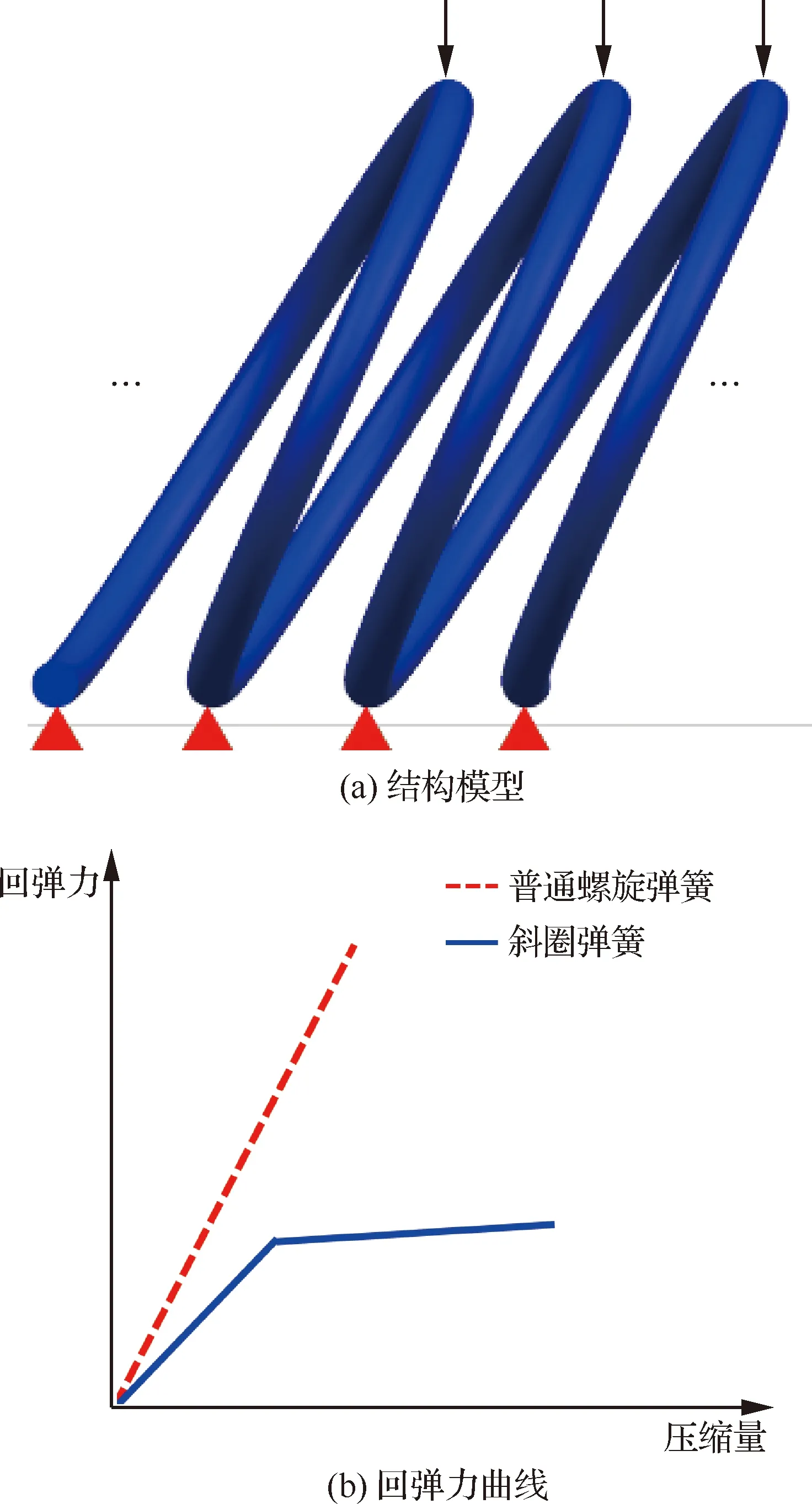
图2 斜圈弹簧结构模型及回弹力曲线Fig.2 Structure model and resilience force curve of canted coil spring
1.2 结构参数
基于斜圈弹簧沿长度方向呈周期性排列的特性,为提高计算效率,在模拟时以单节斜圈弹簧进行分析。利用ANSYS有限元分析软件建立等径圆形截面和中心引导线而后扫掠生成单线圈模型,如图3所示。
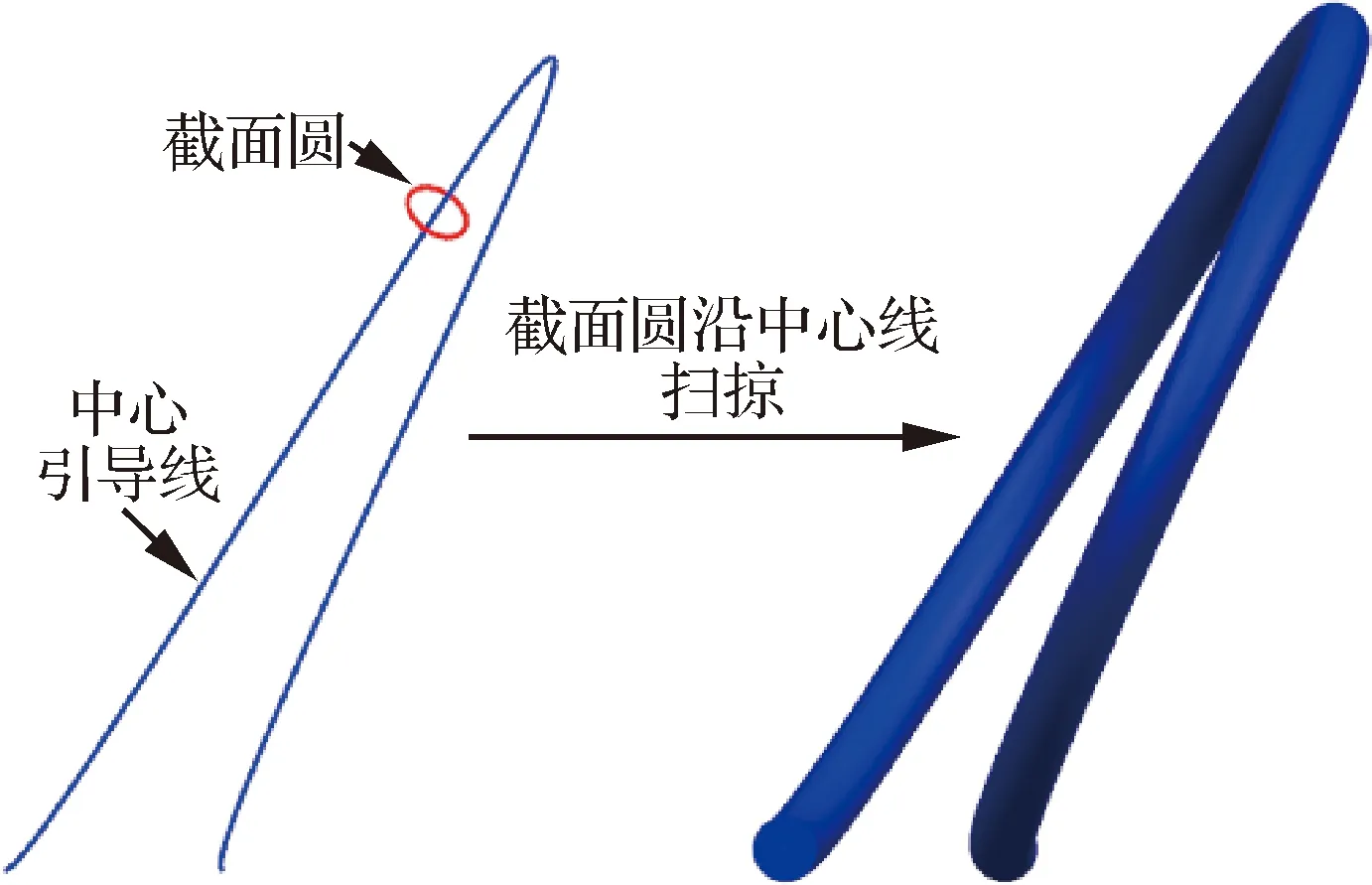
图3 斜圈弹簧引导线模型Fig.3 Model of guide line of canted coil spring
利用参数方程建立图3中的中心引导线,其基本参数定义如图4所示,规定为变量参数,变化范围为0~1。中心线的参数方程为
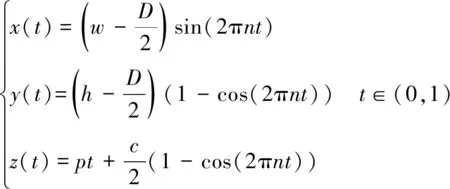
(1)
式中:为斜圈弹簧的宽度;为斜圈弹簧的截面圆直径,即线径;为斜圈弹簧的节数;为斜圈弹簧的高度;为斜圈弹簧的节距;为斜圈弹簧的倾斜程度。
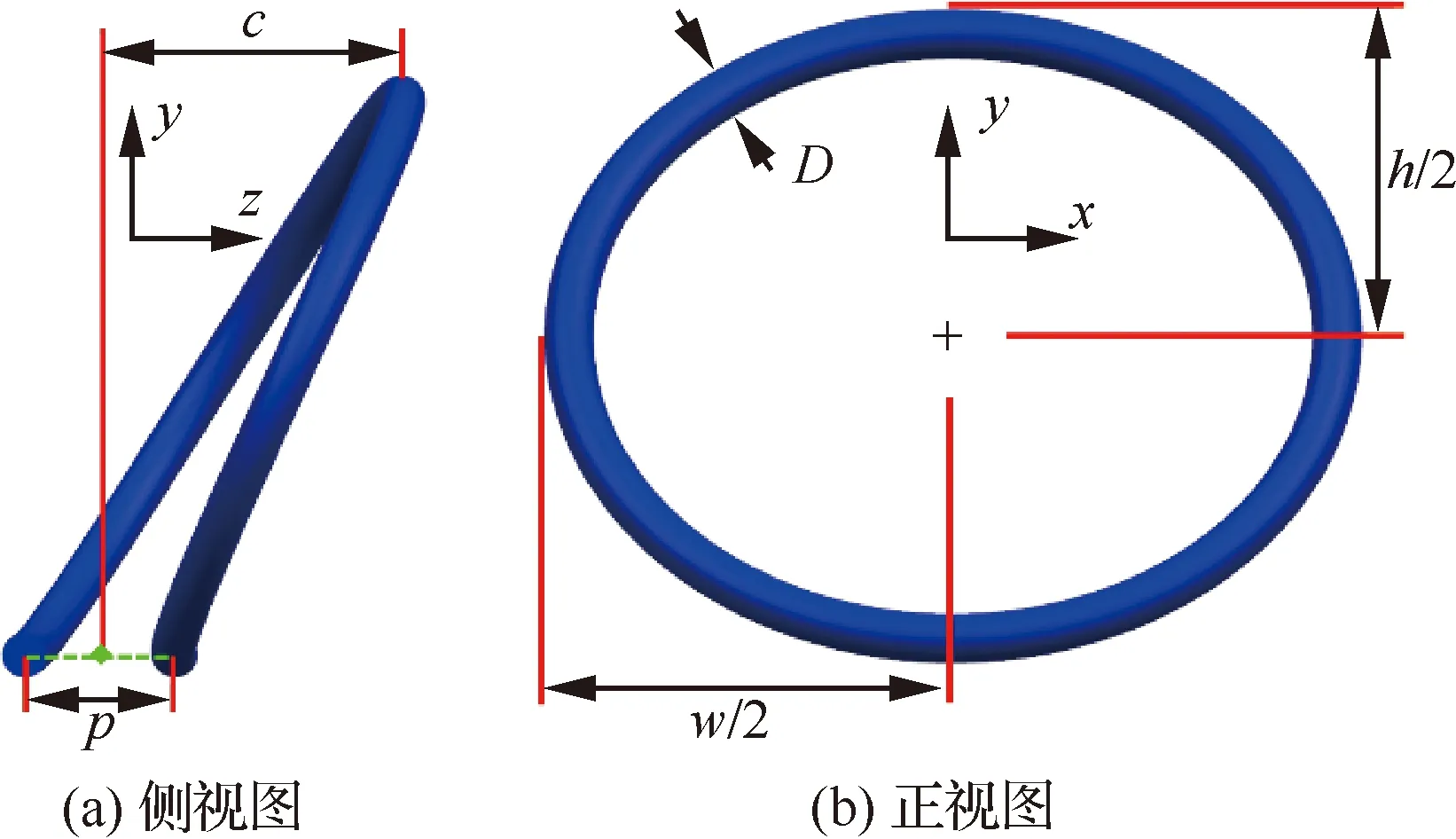
图4 斜圈弹簧模型Fig.4 Canted coil spring model
2 仿真模型前处理与实验校验
2.1 材料属性
斜圈弹簧有限元模拟分析时假设Inconel X-750材料为线弹性材料,其制备的斜圈弹簧在800 ℃ 时仍能够保持较好的力学性能,其材料属性参数如表1所示。
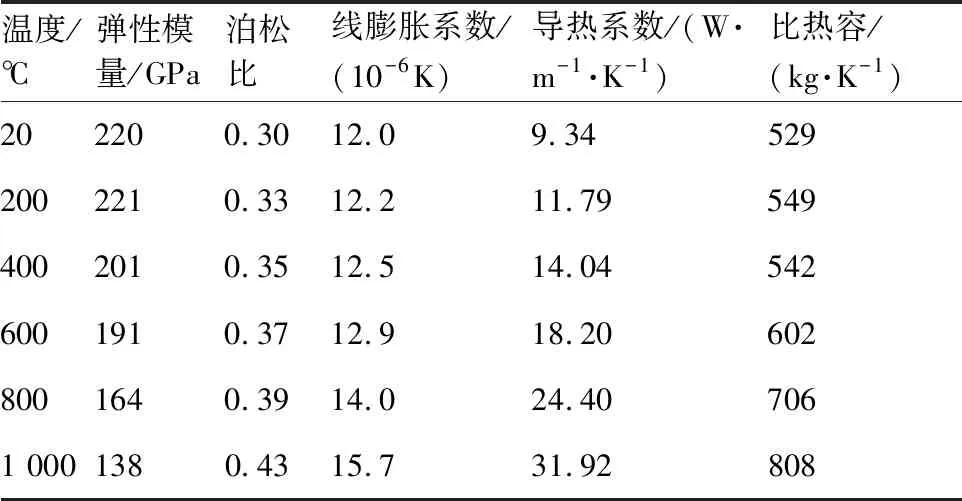
表1 Inconel X-750材料参数[22]Table 1 Material parameters of Inconel X-750[22]
2.2 网格划分和边界条件
为提高模拟计算的可靠性与效率,对斜圈弹簧的模拟分析做出如下假设:
1) 斜圈弹簧每个线圈承受载荷情况相同。
2) 忽略压缩过程中的端部效应。
3) 压缩过程只考虑径向作用力,忽略摩擦力因素。
4) 忽略温度对斜圈弹簧在压缩过程中热应力的影响。
斜圈弹簧模型采用ANSYS软件的Mesh模块进行网格划分,采用Soild187号结构单元,该单元为3维四面体10节点的高精度结构单元,斜圈弹簧的网格划分如图5所示。
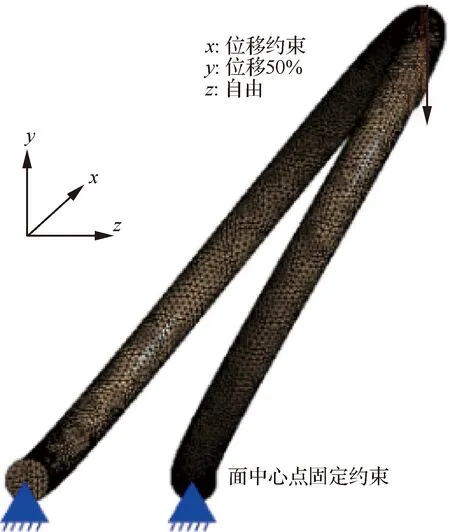
图5 斜圈弹簧网格划分及边界条件Fig.5 Meshing and boundary conditions of canted coil spring
模拟分析时位移载荷施加于斜圈弹簧顶端,由于斜圈弹簧通常以压缩线圈高度的30%~50%状态进行安装,且在线弹性条件下由于回弹力平台影响,在30%~50%压缩量状态下斜圈弹簧的回弹力相差不大。因此位移载荷设定为压缩弹簧高度的50%,方向为斜圈弹簧的径向,即图5中的轴负方向。
为防止斜圈弹簧在压缩过程中发生刚性位移,对斜圈弹簧底部耦合面的中点施加固定约束。为提高结果收敛性,模拟设置50个分析子步,探测斜圈弹簧顶部节点处的作用力以表征斜圈弹簧回弹力。
2.3 实验校验
因主要基于有限元方法对斜圈弹簧进行模拟分析,所以对有限元模拟分析求解设置的可靠性进行实验校验是非常必要的。
实验采用科尔冠公司制备的Ni基合金斜圈弹簧(参数如表2所示)进行常温压缩测试实验,实验设置完全相同的3组重复实验,测量其压缩量-回弹力曲线,并与相同结构参数模型的模拟结果进行对比,从而验证模拟的可靠性。

表2 压缩测试的斜圈弹簧的结构参数
斜圈弹簧径向压缩回弹力测试如图6所示,采用的仪器为万能试验机(压力传感器精度为0.05% FS(Full Scale),量程为100 N),测试步骤如下:
1) 将斜圈弹簧放置在万能试验机载物盘上,并将压盘调节到适当高度,如图6(a)所示。
2) 设置测试程序,如定义接触(压力=0.01 N 时)、下降速度=0.5 mm/min、下降高度为斜圈弹簧高度的20%等。
3) 待测试结束后压盘上升,导出并处理数据。
常温压缩实验的斜圈弹簧圈数=5,在数据处理过程中将实验所测数据除以线圈数=5得到每个线圈的回弹力,将实验数据拟合并与模拟数据对比,结果如图7所示。

图6 斜圈弹簧压缩测试Fig.6 Canted coil spring compression test
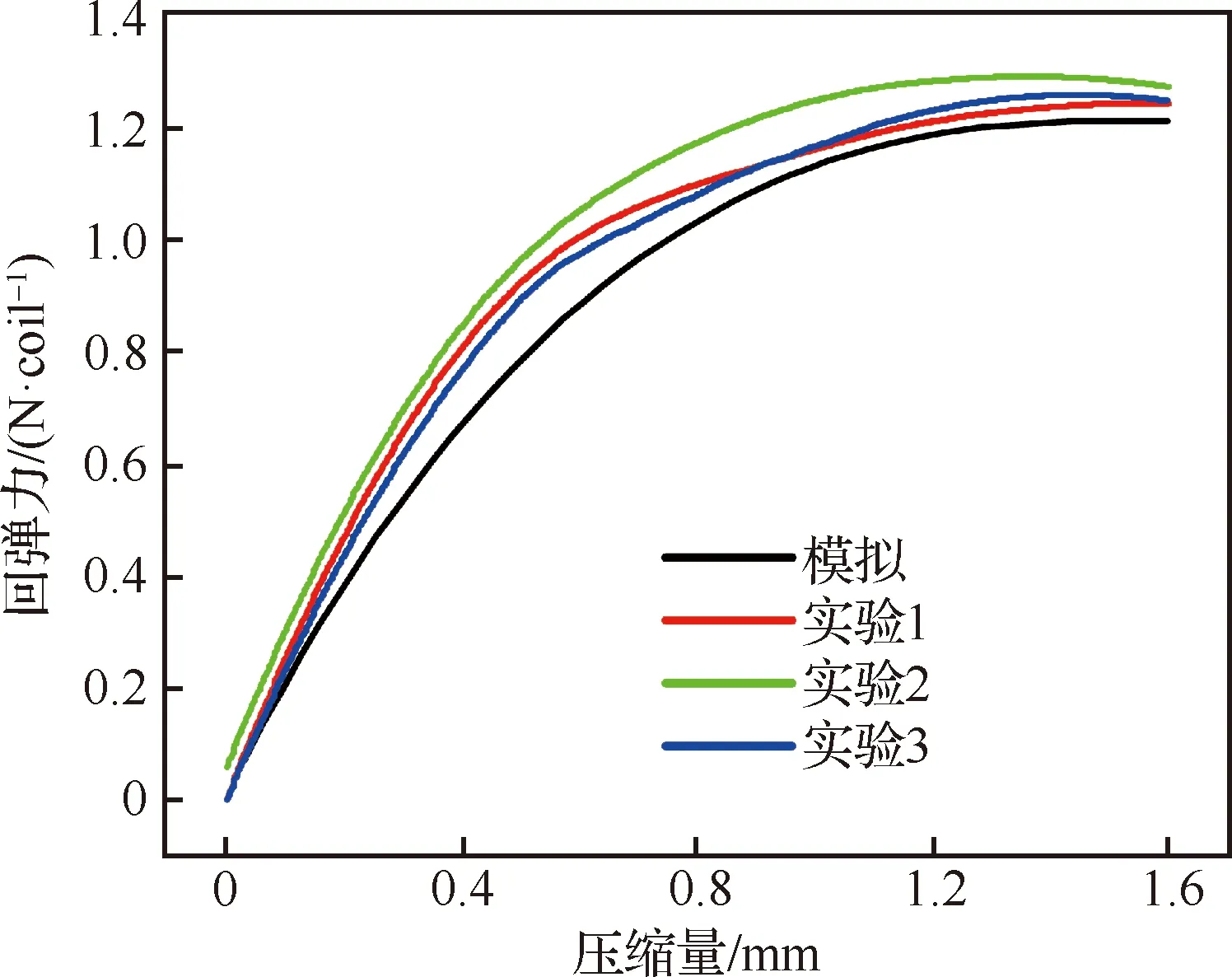
图7 斜圈弹簧模拟结果与实验值对比Fig.7 Comparison of simulation and experimental results of canted coil spring
从图7可看出实验结果拟合曲线与模拟曲线的误差发生主要在增长阶段,回弹力恒定平台也存在较低的偏差量,模拟结果的数值(约为1.2 N/coil)低于实验所测数值(约为1.3 N/coil),误差约为7%,主要是因为在模拟分析时对过程进行了无摩擦假设。图8为斜圈弹簧在压缩过程中的摩擦模型,其中为摩擦系数,可看出在压缩过程中斜圈弹簧的顶部会在压力作用下产生一个与滑动方向相反的摩擦,阻碍斜圈弹簧的转动,实际需更大的力才能使斜圈弹簧的压缩顺利进行,因此实验测得的回弹力高于模拟计算结果。由于Ni基合金斜圈弹簧的服役工况复杂多样,没有固定的服役场景,摩擦系数测定难度大,因此在模拟时设定为无摩擦。

图8 斜圈弹簧的摩擦模型Fig.8 Friction model of canted coil spring
综上分析,采用的有限元模拟分析方法能在很大程度上反映实际的回弹力情况,因此认为有限元模拟分析的设置是可靠的。
3 结果与分析
根据文献[19]并结合斜圈弹簧在动密封领域应用时的常见尺寸,确定讨论斜圈弹簧变形行为时斜圈弹簧的尺寸如表3所示,并以该尺寸为基础设置不同变量,设置宽度-高度、节距-倾斜程度及线径-温度双参数组合,研究多参数共同作用对其回弹力的影响。

表3 斜圈弹簧模拟基础尺寸Table 3 Simulated basic size of canted coil spring
3.1 斜圈弹簧变形行为
通过观察模拟结果发现,斜圈弹簧受50%压缩量的载荷及底部中心约束的作用会发生转动变形,变形过程如图9所示。从图9(a)~图9(c)可看出斜圈弹簧的变形行为可描述为其左右两个线圈分别以底部面中心点为圆心绕轴转动,在转动过程中高度逐渐减小,线圈顶端随压缩逐渐向轴正方向移动,这说明斜圈弹簧在被压缩的过程中顶端会与接触面产生相对滑动,且随压缩过程进展,斜圈弹簧截面的椭圆形离心率逐渐增大,如图9(d)~图9(f)所示。

图9 斜圈弹簧压缩变形过程Fig.9 Deformation process of canted coil spring compression
基于斜圈弹簧的结构特点,可将其看成是由两个半圆梁A、B组成,由于面中心的约束,A、B可视为两个铰支结构,因此在变形过程中会以转动的形式变形。若A、B梁顶点无连接约束,则A、B梁顶点的转动轨迹如图10(a)所示,但由于约束的存在,A梁和B梁的顶端连接点变形量相同,A、B梁顶点的运动轨迹实际为轨迹。因此,在变形过程中A梁将受拉变长,其内侧受拉应力、外侧受压应力,而B梁将受压变短,其内侧受压应力、外侧受拉应力,如图10(b)所示,该分析结论与图10(c)~图10(e)模拟计算得到的结果一致,从法向应力云图中可看出不管是哪个方向的法向应力,A梁的内侧和B梁的外侧应力分布主要为拉伸应力,A梁的外侧和B梁的内侧应力分布主要为压缩应力,验证了图10(b)分析的结论。
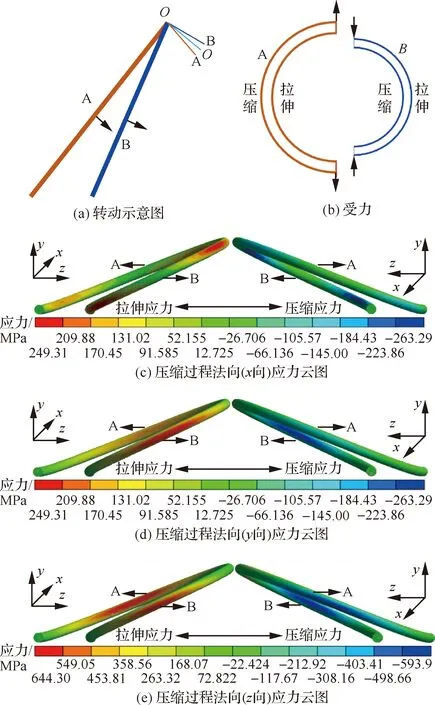
图10 斜圈弹簧变形过程受力分析Fig.10 Force analysis of canted coil spring in deformation process
3.2 高度-宽度对回弹力的影响
斜圈弹簧的高度和宽度受安装槽尺寸的影响,因此将高度和宽度作为双参数组,以研究在这两者共同作用下Ni基合金斜圈弹簧回弹力的变化趋势,模拟模型的尺寸设置如表4所示,表中为温度,不同高度与宽度之间设置正交实验,图11 为高度-宽度双参数组的有限元模拟结果。
从图11(a)的模拟结果可看出Ni基合金斜圈弹簧的回弹力峰值(约为2.87 N/coil)发生在高度和宽度的最小值处,即高度=6.0 mm、宽度=8.0 mm处,最低值(约为1.17 N/coil)发生在高度和宽度的最大值处,即高度=8.0 mm、宽度=12.0 mm。因此可得知Ni基合金斜圈弹簧的回弹力随高度和宽度的增加而降低,该结论与图11(b)回弹力的等高线图显示的结果一致。

表4 高度-宽度模拟模型尺寸Table 4 Height-width simulation model size

图11 高度-宽度耦合模拟结果Fig.11 Simulation results of height-width coupling
高度增加导致回弹力下降的原因在于,当高度增加时斜圈弹簧在压缩转动时的等效力臂也随之增加,如图12(a)所示,根据挠度计算公式式(2)可知在相同压缩率的载荷作用下,斜圈弹簧压缩后的挠度相同,如图12(b)所示。由式(2)可知当等效力臂增加时,需要的驱动力就会降低,因此斜圈弹簧的回弹力表现出随高度增加而降低的趋势。
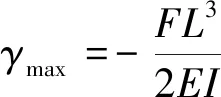
(2)
式中:为材料的拉伸模量;为截面惯性矩;为抗弯刚度。
增加宽度导致回弹力下降的原因在于,当其他参数保持不变时,宽度增加,组成斜圈弹簧的两个半圆梁的周长及阔度也会增加,如图10(b)所示,周长和阔度的增加导致线圈的等效力臂也随之增加,根据式(2)可知当力臂增加时,保持相同的压缩率,所需的驱动力就会下降,因此斜圈弹簧的回弹随宽度的增加而减小。
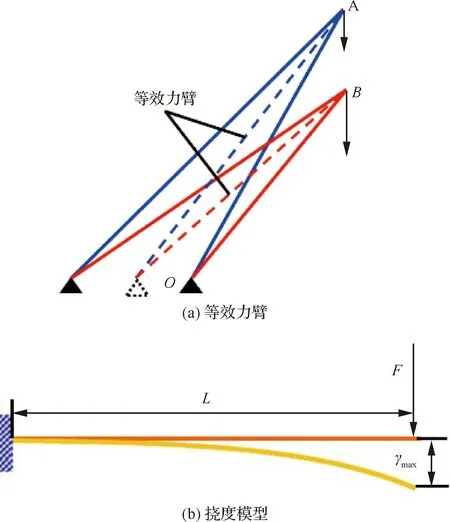
图12 斜圈弹簧的等效力臂及挠度模型Fig.12 Equivalent lever arm and deflection model of canted coil spring
3.3 节距-倾斜程度对回弹力的影响
斜圈弹簧的节距和倾斜程度共同影响斜圈弹簧的长度,因此将节距和倾斜程度作为双参数组,以研究在这两者共同作用下Ni基合金斜圈弹簧回弹力的变化趋势,模拟模型的尺寸设置如表5所示,在不同节距与倾斜程度之间设置正交实验,图13 为节距-倾斜程度双参数组的有限元模拟结果。

表5 节距-倾斜程度模拟模型尺寸Table 5 Pitch-cant amplitude simulation model size
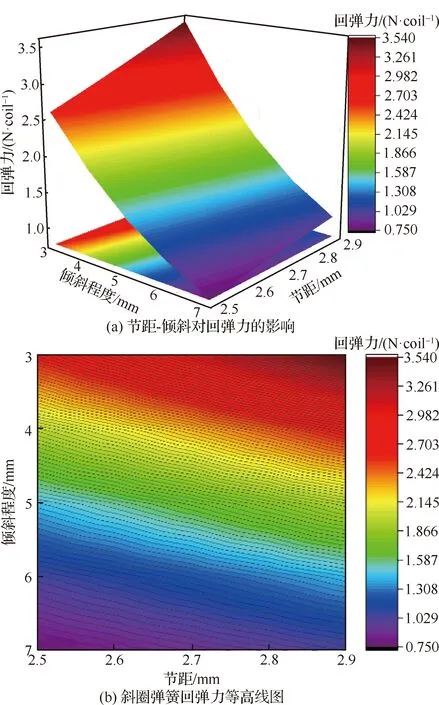
图13 节距-倾斜程度耦合模拟结果Fig.13 Simulation results of pitch-cant amplitude coupling
从图13(a)可知,小节距、大倾斜程度的斜圈弹簧具有较小的回弹力(如=2.5 mm、=7.0 mm 时回弹力约为0.75 N/coil),而大节距、小倾斜程度的斜圈弹簧具有较大的回弹力(如=2.9 mm、=3.0 mm时回弹力约为3.54 N/coil),对于单参数,在其他参数保持不变的情况下,斜圈弹簧的回弹力随倾斜程度的增大而降低,随着节距的增大而增大,该变化趋势与图13(b) 回弹力等高线图显示的结果一致。
增加斜圈弹簧的倾斜程度导致回弹力下降的原因在于,斜圈弹簧倾斜程度增大时,弹簧在压缩过程中的等效力臂也随之增大,如图14所示,在相同的压缩率载荷作用下,根据式(2)可知当力臂增大时,其所需的作用力就会下降,而斜圈弹簧的回弹力来源就是变形过程中的变形抗力,根据作用与反作用的原理可知,当倾斜程度下降时其回弹力也随之下降。
B在其他参数保持不变的情况下,当节距增大时B′梁的底端与A梁距离增大,如图15所示,大节距的B′梁比小节距的B梁跨距更大,在压缩过程中大节距的B′梁对线圈顶端点的支撑作用更为明显,机械结构强度更大,使线圈在压缩过程中更难产生转动变形,因此斜圈弹簧的回弹力随节距增大而增大。

图14 不同倾斜程度的斜圈弹簧简化模型Fig.14 Simplified model of canted coil spring with different cant amplitude
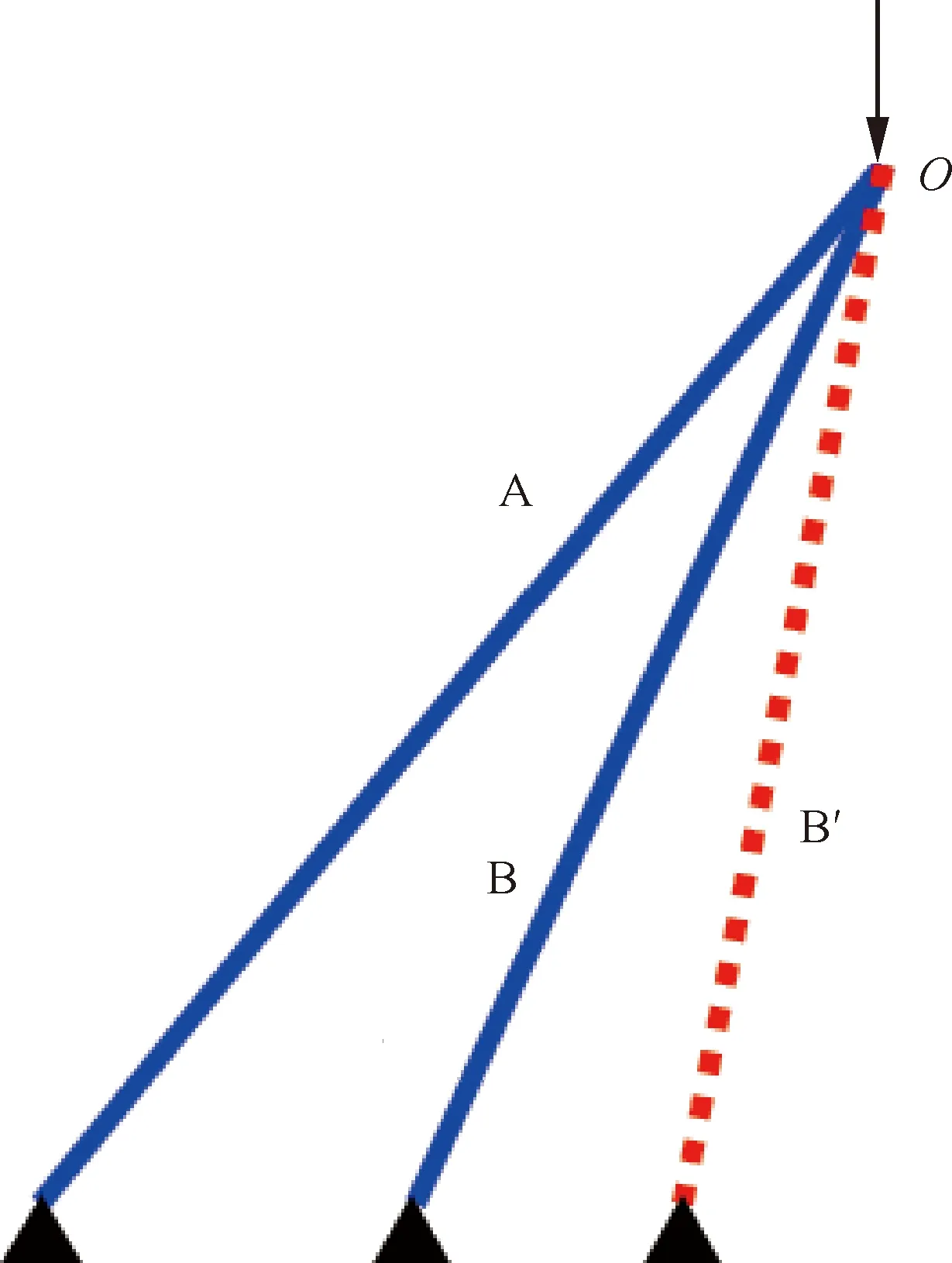
图15 不同节距的斜圈弹簧简化模型Fig.15 Simplified model of canted coil spring with different pitch
3.4 线径-温度对回弹力的影响
斜圈弹簧的线径和温度共同影响着斜圈弹簧的整体刚度,因此将线径和温度作为双参数组,以研究在这两者共同作用下Ni基合金斜圈弹簧回弹力的变化趋势,模拟模型的尺寸设置如表6所示,不同线径和温度之间设置正交实验,图16为线径-温度双参数组的有限元模拟结果。

表6 线径-温度模拟模型尺寸Table 6 Wire diameter-temperature simulation model size

图16 线径-温度耦合模拟结果Fig.16 Simulation results of wire diameter-temperature coupling
线径-温度对斜圈弹簧回弹力的影响主要体现为改变斜圈弹簧的刚度特性,大线径、低温度下的斜圈弹簧刚度较高,在被压缩时抵抗外力的作用更强烈,因此其具备的回弹力也就越大,该结果在图16(a)和图16(b)中有较为明显的体现,当=0.9 mm、=20 ℃时,回弹力约为4.8 N/coil;当=0.5 mm、=800 ℃时,回弹力约为0.3 N/coil。
线径对斜圈弹簧刚度的提高可解释为提高其抗弯刚度。斜圈弹簧回弹力的产生体现为压缩时为抗弯过程,即会产生一定的弯矩,弯矩公式为
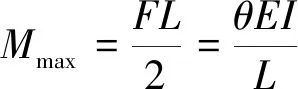
(3)
式中:为转角。在其他参数不变的情况下,承受相同压缩率时,压缩过程的转角和力臂是相同的,因此斜圈弹簧的回弹力正比于斜圈弹簧的抗弯刚度,截面为圆的截面惯性矩计算公式为
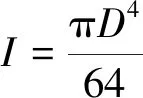
(4)
由式(3)和式(4)可得∝∝,可看出回弹力与线径的四次方成正比,即回弹力随斜圈弹簧的线径变化呈现出高阶非线性关系,该结论在图16(b)回弹力等高线图中可得到验证。从图16(b)中可看出在同一温度下,线径越大,等高线就越密集,说明增大线径可明显提高斜圈弹簧的回弹力,线径是回弹力的敏感参数。
高温会使斜圈弹簧回弹力下降,这是因为当温度升高时,制备斜圈弹簧的Ni基合金的弹性模量会降低(见表1),由式(3)可知当弹性模量下降时,斜圈弹簧所需的抗弯弯矩也会随之下降,变形抗力减小,回弹力降低。
由此可知线径和温度都是通过抗弯刚度影响斜圈弹簧的回弹力,线径增大引起惯性矩增大,从而引起回弹力升高,温度降低引起弹性模量下降,从而引起回弹力降低。
综上所述,增加斜圈弹簧的高度、宽度及倾斜程度,斜圈弹簧的回弹力表现出降低趋势;而增加节距和线径可使回弹力提高;温度升高使弹性模量降低引起金属软化,从而引起回弹力降低。这给回弹力设计提供了一定的指导性。
3.5 可设计性分析
Ni基合金斜圈弹簧在动密封结构的运用中,要求回弹力在设计要求的范围内,不能过大或过小,过大会导致密封接触面上防热涂层的破坏并增加阻力影响机械结构的运动;过小则会引起密封失效。因此斜圈弹簧的回弹力设计尤为关键,其设计流程如图17所示,首先根据安装槽尺寸确定线圈高和线圈宽;其次根据回弹力设计要求初步确定线径、节距和倾斜程度;而后对初步设计的斜圈弹簧进行回弹力模拟分析;最后根据模拟结果对线径、节距和倾斜程度尺寸进行优化设计。
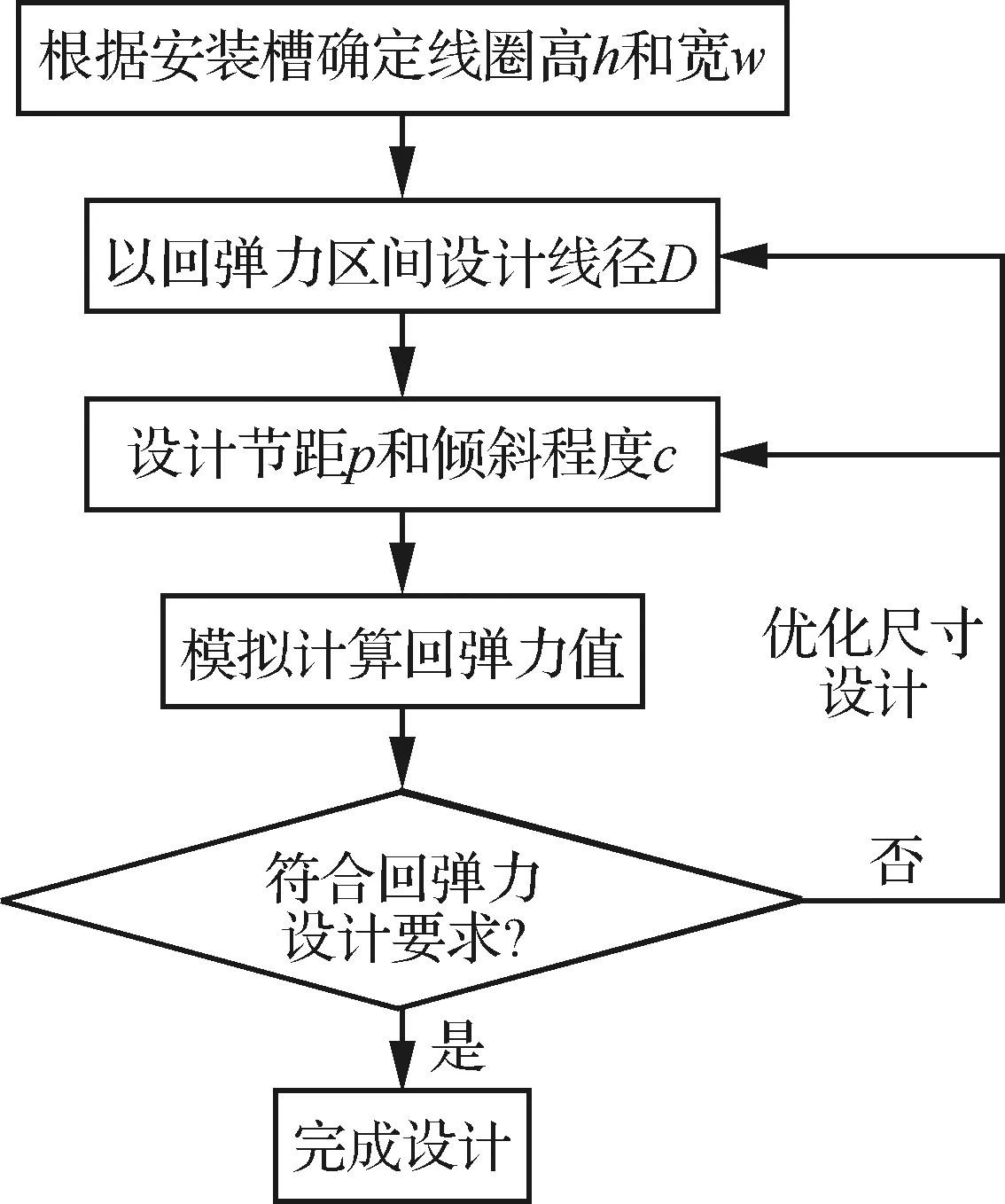
图17 斜圈弹簧设计流程图Fig.17 Canted coil spring design process
以密封部位中密封槽可供斜圈弹簧放置的尺寸深度为5.5 mm、宽度为11 .0 mm为例,在30%压缩量的前提下,斜圈弹簧的回弹力在室温条件下为1.2~1.5 N/coil时才能达到最佳动密封效果。根据3.1~3.4节可初步设计符合要求的斜圈弹簧,具体步骤如下:
1) 确定宽度和高度
斜圈弹簧的高度和宽度受安装槽及压缩量的制约,因此可根据30%压缩量及安装槽的深度为5.5 mm的条件,计算出斜圈弹簧的高度约为8.0 mm。
由于斜圈弹簧安装时斜圈弹簧与安装槽为间隙配合,因此斜圈弹簧的宽度设计为10.0 mm。
2) 初步确定线径尺寸
根据室温下回弹力为1.2~1.5 N/coil的要求,通过图16(b)的回弹力等高线图可初步确定斜圈弹簧的线径为0.6 mm。
虽然图16(b)是50%压缩量条件下的计算结果,但由于斜圈弹簧在30%~50%压缩量时处于回弹力平台区间,因此两者回弹力相差不大。
3) 初步确定节距与倾斜程度尺寸
节距与倾斜程度尺寸可根据图11(b)的等高线图初步设计为节距=2.7 mm、倾斜程度=5.0 mm。因此初步设计尺寸如表7所示。
4) 模拟分析
以初步设计尺寸进行模拟分析,得到压缩率-回弹力曲线,如图18所示。可看出斜圈弹簧在30%~50%压缩量范围内有较为明显的回弹力平台,回弹力约为0.89 N/coil,低于设计要求的值,因此需通过调节倾斜程度、节距和线径进行优化设计。
5) 优化设计
根据3.3和3.4节,为将斜圈弹簧的回弹力提高到1.2~1.5 N/coil,可通过减小倾斜程度、提高节距及增大线径提高回弹力。因此设计的优化尺寸如表8所示,Ⅰ组为增大线径的优化尺寸,Ⅱ组为减小倾斜程度的优化尺寸,Ⅲ组为增大节距的优化尺寸,Ⅳ组为减小倾斜程度和增大节距的双参数优化尺寸。

表7 初步设计尺寸Table 7 Preliminary design size
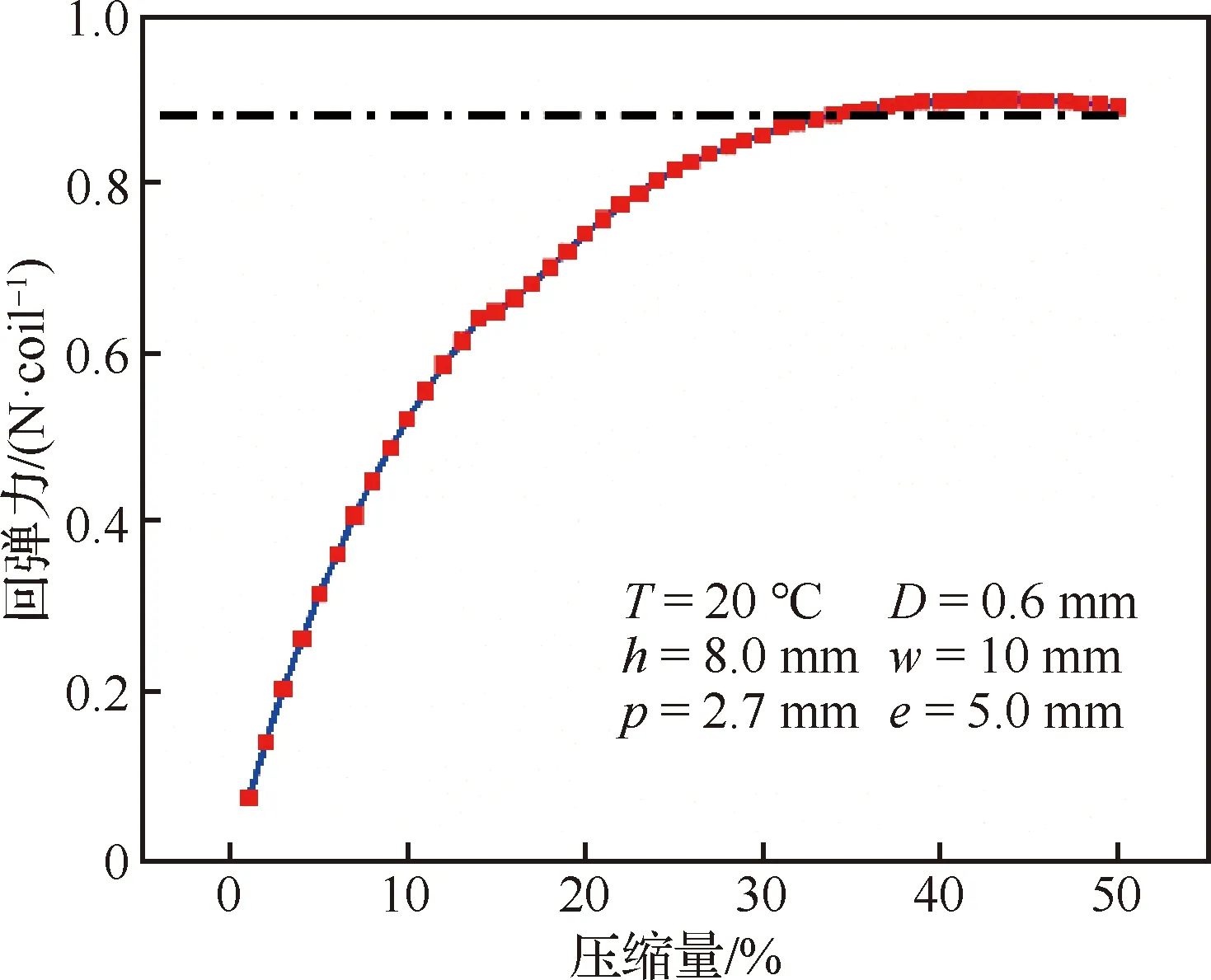
图18 初步设计尺寸的模拟结果Fig.18 Simulation results of preliminary design dimensions

表8 优化设计尺寸Table 8 Optimized design size
6) 优化设计的模拟计算
图19为表8中4组优化尺寸的模拟结果,可看出Ⅱ组和Ⅳ组的斜圈弹簧在30%压缩量时回弹力为1.2~1.5 N/coil,因此Ⅱ组和Ⅳ组的尺寸为符合设计要求的斜圈弹簧尺寸。
从优化设计的Ⅰ组尺寸可看出,增大线径可成倍提高回弹力;从初始尺寸与Ⅲ组、Ⅱ组与Ⅳ组的结果对比可看出,增大节距后回弹力的增幅不大,因此在设计时可通过节距对回弹力进行微调。
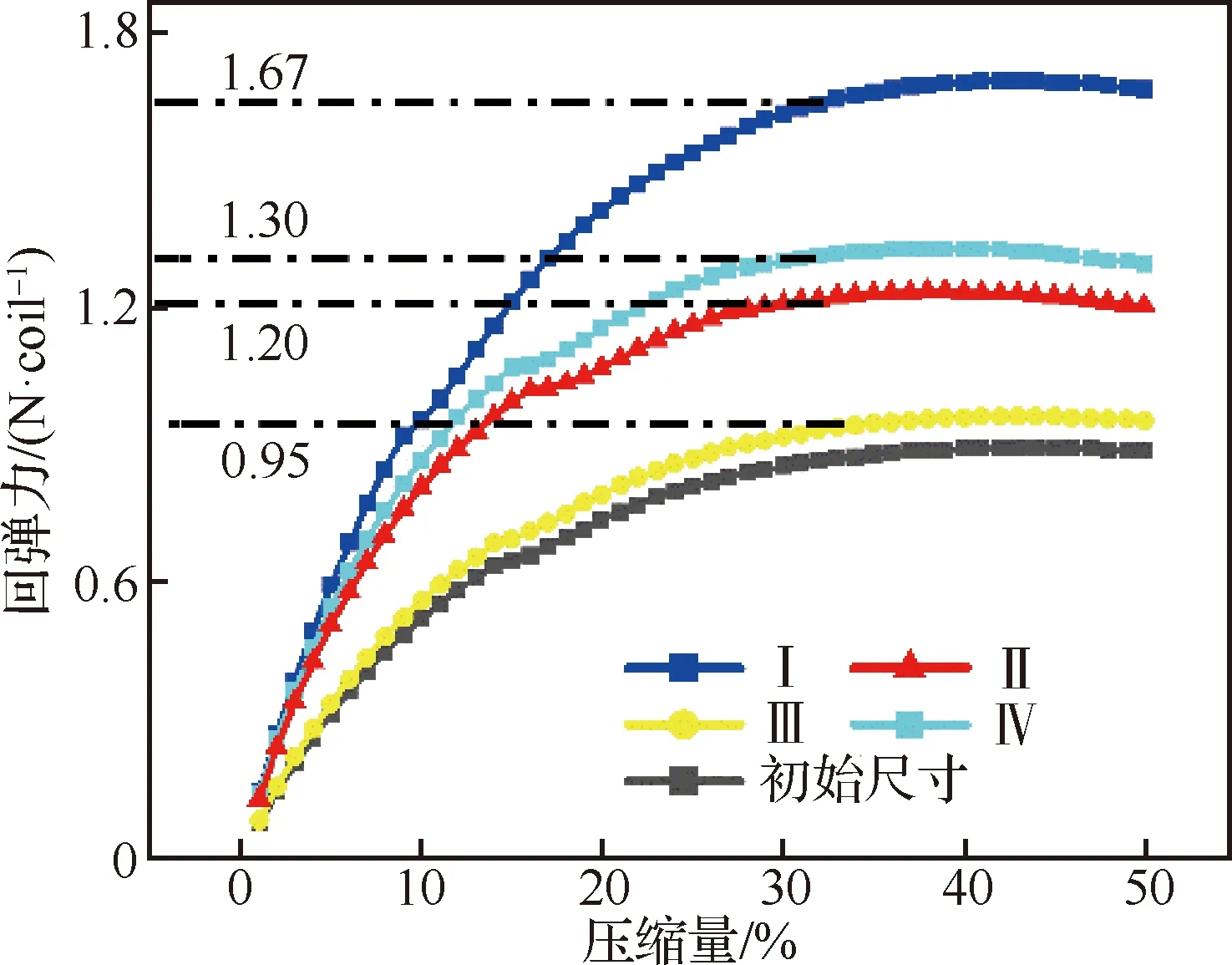
图19 优化设计尺寸的模拟结果Fig.19 Simulation results of optimized design dimensions
综上所述,根据研究内容及设计流程基本可实现对斜圈弹簧的可设计性,为工业上斜圈弹簧的尺寸设计提供一定指导建议。
4 结 论
本文通过参数方程对Ni基合金斜圈弹簧进行参数化建模,而后基于ANSYS有限元分析软件对斜圈弹簧进行模拟分析,可得出以下结论:
1) 通过实验所测结果与模拟计算结果对比可知,采用的有限元模拟分析求解设置是可靠的。
2) 斜圈弹簧在压缩过程中的变形行为是两个半圆梁线圈分别以底部面中心点为圆心绕轴转动,截面视图的离心率随压缩增加逐渐增大。
3) 增加斜圈弹簧的高度、宽度及倾斜程度,斜圈弹簧回弹力表现出降低的趋势;增加节距和线径可使回弹力增加,且线径与回弹力表现为高阶非线性关系;温度越高,Ni基合金斜圈弹簧弹性模量越低,抗弯刚度也就越低,从而使斜圈弹簧的回弹力越低。
