基于SVD的雷达嵌入式通信波形设计方法

李保国，张澄安,*，徐建秋

1. 国防科技大学 电子科学学院，长沙 410073 2. 中国人民解放军31103部队，南京 210000

随着无线电技术的进步，无线通信已经取得长足发展。但对于军事无线通信而言，其应用可能面对2个挑战，一是由于传统无线通信的开放性和广播性，电磁信号极易被捕获、识别和干扰，在战场条件下，大量的指令、情报等关键信息通过无线通信传输，极易造成情报泄露，尤其是面对现代无源定位技术的进步，传统无线通信注定不能适应现代战场需求；二是在未来信息化战场条件下，指令传输、情报共享的数据将是海量的，如何提高频谱资源的利用效率，也是未来军事通信必须面对的问题。

2013年，美国国防预研计划局(Defense Advanced Research Projects Agency，DARPA)启动了名为“雷达与通信的频谱接入共享”(Shared SPectrum Access for Radar and Communications，SSPARC)的项目研究，旨在开发军用雷达和军事通信系统之间的频谱共享技术。作为SSPARC项目有力竞标者之一，雷达嵌入式通信(Radar-Embedded Communication, REC)能够在实现雷达和通信共享频谱的同时满足军事通信隐蔽性的需求。

REC的工作原理如图1所示，首先，REC工作区域被友方或敌方雷达照射，友方目标和合作接收机都可以收集到雷达信号；其次，友方目标携带可以对雷达信号进行感知的射频(Radio Frequency，RF)标签，RF标签可以对雷达信号进行采集，生成具有隐蔽特性的通信信号，与雷达散射回波同步发送，而RF标签周围的局部散射回波则作为通信信号的隐藏载体；最后，合作接收机已知通信信号的设计方式，可以实现对通信信号的有效提取，恢复出友方目标所嵌入的通信信息，完成隐蔽通信。

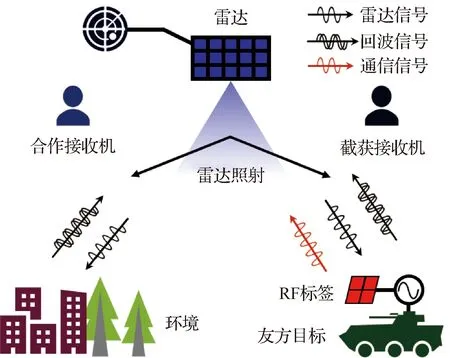
图1 REC工作原理图[5]Fig.1 Diagram of REC working principle[5]

在图1的REC工作过程中，由RF标签嵌入的通信信号与雷达后向散射回波信号同时同频，且在功率上远低于雷达回波信号，因此REC具有实现雷达与通信频谱共享和抗截获隐蔽通信的双重作用。

在隐蔽通信概念中，低检测概率(Low Probability of Detection, LPD)特性指通信信号难以被截获接收机检测到的特性，低截获概率(Low Probability of Intercept, LPI)特性指通信信号在被检测到的情况下，难以被截获接收机分类识别的特性。传统的隐蔽通信技术主要包括直接序列扩频技术、跳频技术、跳时技术、噪声通信技术以及各种加密算法等。其中，除直接序列扩频技术外，其余隐蔽通信技术在信号层是可检测的，因此不具有LPD特性，只具有LPI特性，而面对敌方无源定位等先进的探测技术时将会导致目标位置等敏感信息的暴露，带来极大的安全隐患。而直接序列扩频技术与REC技术的隐蔽原理相似，都是将低功率的通信信号淹没在背景信号中，都同时具有LPD和LPI特性，但直接序列扩频通信的带宽远远大于被传输的原始信息的带宽，不利于提高频谱利用效率，且其提出较早，已经有很多成熟的检测方法，因此在未来信息化战场条件下，REC相较于其他隐蔽通信在隐蔽性能上具有独特的优势。

REC可分为脉间REC和脉内REC。20世纪90年代，脉间REC首先被提出并成功应用于合成孔径雷达，其原理是在多个雷达后向散射回波信号中传递雷达信号的相移序列，并且传输一个通信波形要用到多个雷达脉冲(通常数百个)，因此传输速率很低。2007年，脉内REC由美国堪萨斯大学Blunt教授团队首次提出，可以在一个雷达脉冲回波中嵌入一个通信波形，大大提高了REC的通信速率。为了便于表达，本文下述REC技术均指脉内REC技术。

文献[5]率先对REC进行了系统建模，并提出了REC波形设计的3种方法：非主空间特征向量作为通信波形(Eigenvectors-as-Waveforms，EAW)、非主空间特征向量加权(Weighted-Combining，WC)和主空间投影(Dominant Projection，DP)。此外，文献[5]还提出了2种REC接收算法：匹配滤波器(MF)和去相关滤波器(DF)，用于REC合作接收方接收机设计。2009年，文献[14]研究了多径衰落对ERC性能的影响，对EAW、WC和DP这3种通信波形在多径信道下的鲁棒性能进行了分析，并得出结论：DP波形具有良好的抗多径特性。文献[15-16]将信道信息引入REC波形设计，采用时间反转技术来实现通信信号的空间聚集，提高了通信可靠性和LPI特性。2010年，文献[17]提出了一种基于归一化相关系数来评价REC抗截获性能的定量评价方法，使REC的LPI特性得到量化。2011年，文献[18]提出了一种基于纽曼-皮尔逊(Neyman-Pearson, NP)准则的两级REC接收方法，可以实现REC通信信号的恒虚警检测。2015年，文献[19]提出了2种新的REC波形设计方法：成型主空间投影(Shaped Dominant Projection，SDP)和注水成型(Shaped Water-Filling，SWF)波形设计方法，具有更好的LPD特性。2020年，文献[20]又提出了一种逆成型主空间(Inverse Shaped Dominant Projection，ISDP)波形设计方法，降低了通信信号对雷达系统的干扰。

除了Blunt教授团队对REC做出了主要工作外，该领域还引起了许多国内外其他学者的关注和研究。2015年，意大利学者Ciuonzo等提出了一种基于多目标优化的波形设计方法，该方法可以灵活在通信可靠性和隐蔽性之间进行权衡。2016年，麦超云等针对稀疏雷达波形进行了REC波形的设计，提高了通信信号的频带利用率。2017年，Sahin等将连续相位调制(Continuous Phase Modulation, CPM)技术引入REC系统，并提出了一种可以降低算法复杂度的波形设计方法。2019年，Nusenu等提出了一种基于频率分集多输入多输出(Frequency Diverse Multiple-Input Multiple-Output, FD-MIMO)的REC方案，进一步拓展了REC的应用范围。

自REC的概念被提出以来，通信波形设计一直是REC的关键技术，许多学者也对此进行了研究。然而，过去所有的波形设计方法都是对雷达信号进行了转换，然后通过特征值分解进行波形设计，其并没有直接针对雷达信号进行研究。这样会带来一些问题，一是所设计的REC通信波形与雷达信号相似程度下降，通信隐蔽性能会有所损失；二是无法对雷达回波和REC通信波形之间的相似程度进行量化，不能在通信隐蔽性和可靠性之间进行权衡；三是所设计的通信波形并不完全正交，这会导致通信性能的损失。针对这3个问题，本文提出了一种基于奇异值分解(Singular Value Decomposition，SVD)的REC波形设计方案，可以很好地解决上述传统REC波形设计缺陷，增加REC波形的通信可靠性和抗截获性能。

本文的贡献主要有以下几点：

1) 基于SVD分解提出了一种具有更高通信可靠性和更低被截获概率的REC波形生成算法，给出了算法的具体步骤。

2) 从数学上对SVD波形和雷达波形的相似度进行了推导计算，为进行通信波形的隐蔽性和可靠性权衡提供了参考。

3) 对SVD的通信可靠性进行了进一步分析，并与传统3种REC波形通信可靠性进行了比较。

4) 对SVD波形的LPI特性进行了仿真分析，证明了SVD波形具有更好的抗截获性能。

5) 对SVD波形的计算复杂度进行了理论分析，并与传统3种波形设计方法进行了对比。

1 系统模型构建

1.1 REC信道模型

REC信道建模如图2所示，其信号传输路径可以分为前向链路和后向链路，前向链路为雷达照射链路，后向链路为收发链路。雷达信号经过雷达照射链路照射REC工作区域，环境和友方目标会对雷达信号进行散射而产生散射回波，而友方目标所携带的RF标签则会对雷达信号进行感知，对雷达信号进行重构生成具有LPI特性的REC通信波形，与雷达后向散射回波同步发送给合作接收机。合作接收机接收到的信号为雷达回波、REC通信信号和环境噪声三者的混合信号：

()=()*()+()*()+()

(1)

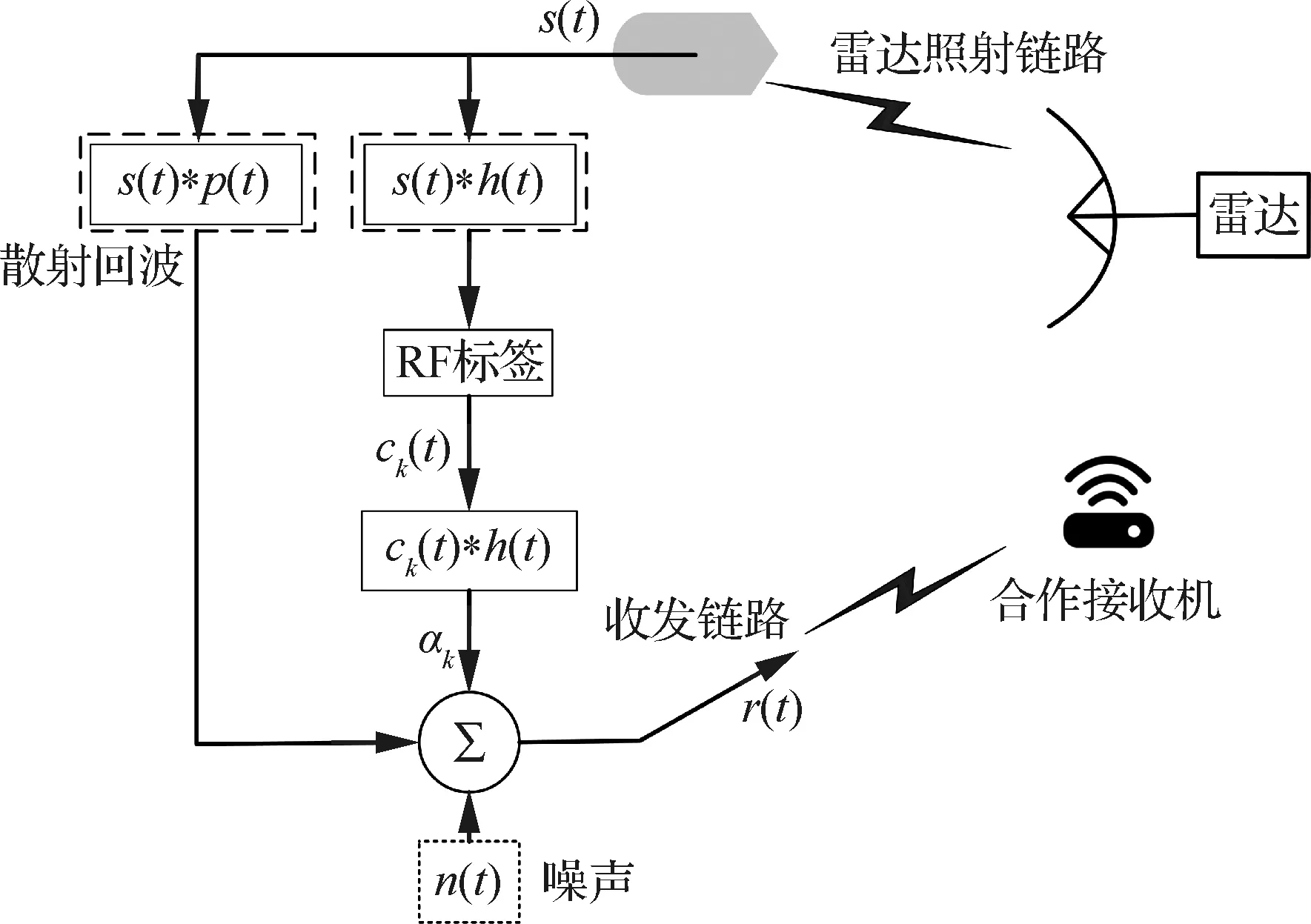
图2 REC信道模型Fig.2 REC channel model

式中：()为合作接收机接收到的混合信号；()为雷达信号；()表示环境散射样本；()代表信道多径响应；()表示第个通信波形被嵌入；表示()的功率约束因子；()为环境噪声。其中，雷达后向散射回波信号建模为雷达信号()和环境散射样本()的卷积。

进一步将式(1)离散化，定义为满足雷达信号奈奎斯特采样准则的采样点数，为过采样因子。因此雷达信号可以被离散地表示为

=[,,…,]

(2)

式中：,,…,为雷达过采样数据。通过对进行循环移位构建托普利兹矩阵：

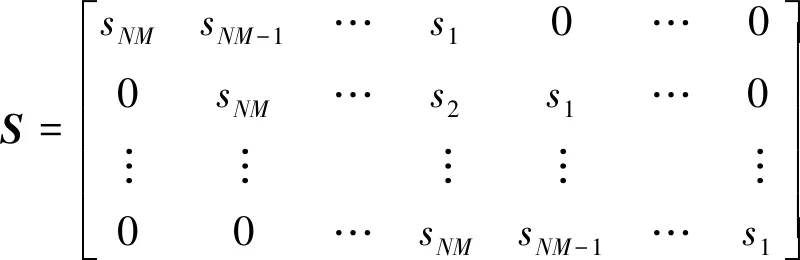
(3)

式中：∈×(2-1)。则卷积过程()*()可以近似离散表示为

·=

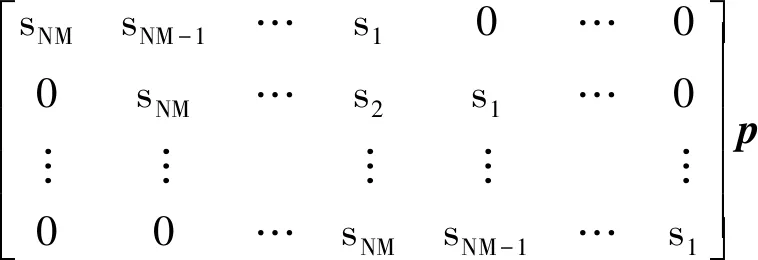
(4)

式中：为后向散射样本()的离散化；∈2-1。不考虑信道多径，式(1)可被离散化为

=·++

(5)

式中：,∈，分别代表通信信号和环境噪声的采样值。

1.2 雷达回波特征提取模型

REC系统需要生成与雷达后向散射回波具有相关性的通信波形来保证系统LPI特性，因此要首先对雷达后向散射回波进行特征提取。

以雷达信号为LFM脉冲信号为例，假设后向散射样本为高斯噪声，通过式(4)构建的雷达后向散射回波的频谱如图3所示。将雷达回波频谱可以分为通带成分和过渡带成分，其中过渡带成分主要是由于环境散射而造成的频谱扩展。

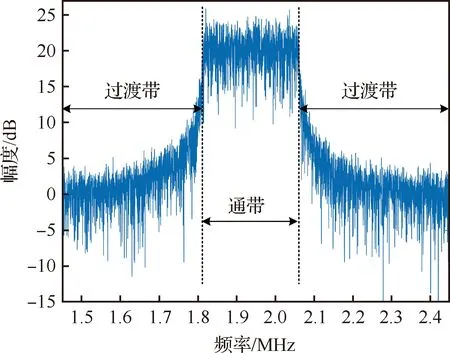
图3 雷达后向散射回波的频谱图Fig.3 Spectrogram of radar backscatter echo

由式(4)，环境后向散射为托普利兹矩阵列向量加权，因此可以对矩阵进行左奇异值分解来提取环境后向散射回波特征：

=

(6)

式中：∈×为酉矩阵；=diag(,,…,)为对角阵，≥≥…≥≥0；表示的共轭转置。

同样以雷达信号为LFM脉冲信号为例，取=100，分别取2和4，对应的特征值曲线如图4所示。进一步将根据特征值大小定义前个特征值对应的特征向量成分为后向散射回波的主空间，后-个特征值对应的特征向量成分为后向散射回波的非主空间，分别对应雷达回波频谱的通带成分和过渡带成分。因此将式(6)进一步表示为

(7)

式中：∈×由前个主空间特征向量组成；∈×(-)由-个非主空间特征向量组成；∈×为前个主空间特征值对角阵；∈(-)×(-)为-个非主空间特征值组成的对角阵。

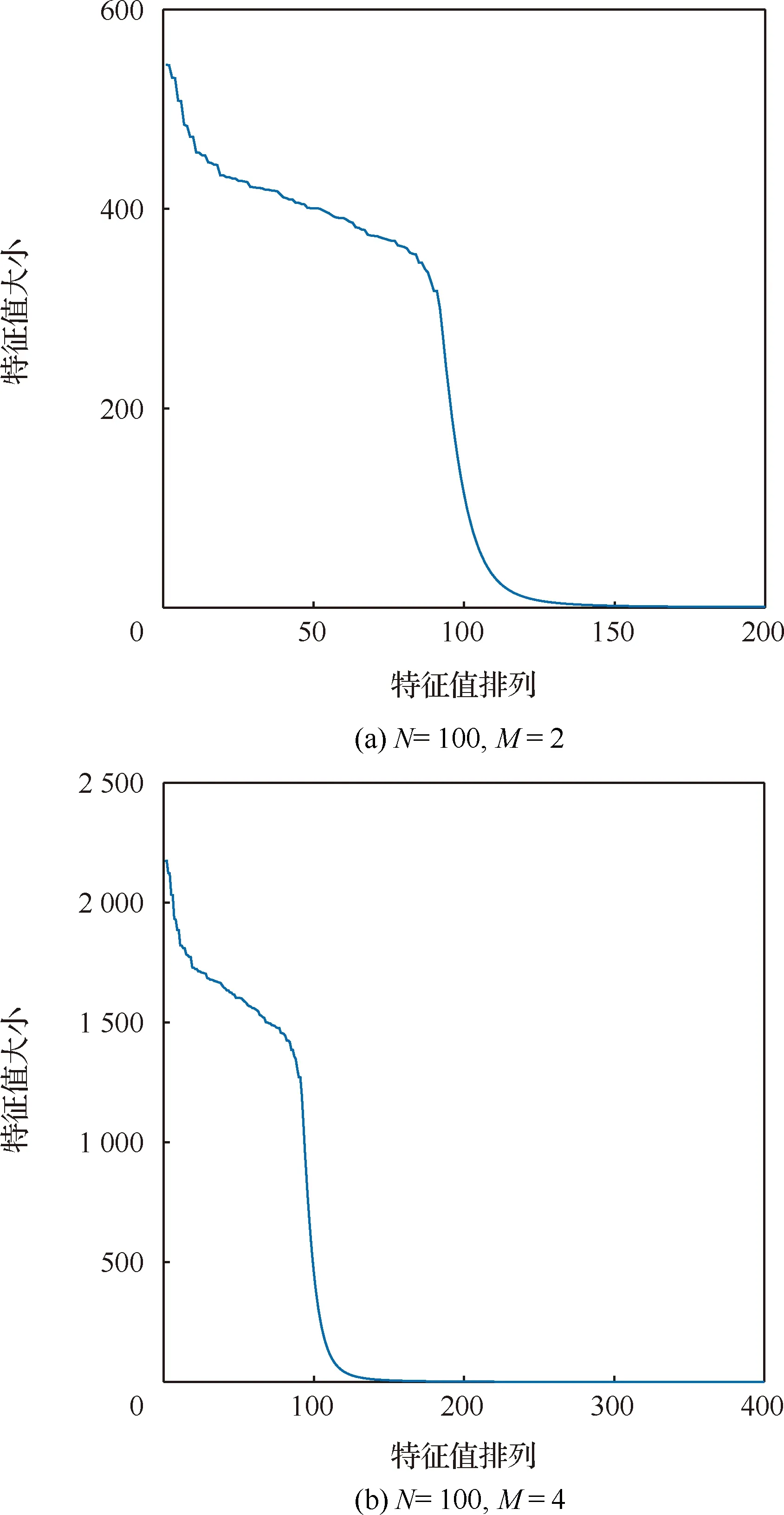
图4 雷达后向散射回波特征值曲线Fig.4 Eigenvalue of radar backscatter echo

2 传统REC波形设计方法与接收策略

REC波形设计的目的是构造出一组含有个波形的波形集，每个波形可代表log位二进制比特信息。这一节主要对传统的REC波形设计方法和REC接收机算法进行介绍，并进一步对传统REC波形的正交性进行分析。

2.1 传统REC波形设计方法

基于第1节建立的模型，传统的REC波形设计方法主要有3种：EAW、WC、DP，下面介绍这3种波形设计方法。

1) EAW

EAW方法直接使用非主空间的特征向量作为REC波形，即

==1,2,…,

(8)

式中：∈为非主空间矩阵的列向量。

2) WC

WC方法对非主空间的特征向量进行加权，即

==1,2,…,

(9)

式中：∈-是由合作发送方和合作接收方共同约定的权值列向量，其可以为随机向量，但必须为收发方已知。

3) DP

DP方法考虑通过投影的方式来产生通信波形。其算法过程为

产生投影矩阵

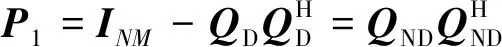
(10)

式中：投影矩阵∈×；为×的单位矩阵。然后将投影矩阵和收发方已知的列矢量相乘得到第1个REC通信波形

=

(11)

式中：通信波形∈;列矢量∈，其也可以为随机矢量，但必须为收发方已知。通过投影操作产生的通信波形与主空间正交，与非主空间相关，非主空间占据雷达散射回波非主要成分，因此通信波形和雷达散射回波呈现弱相关状态。

为了更好地接收性能，REC通信波形之间要尽量正交，因此在设计第2个通信波形时将加入矩阵中形成新矩阵

(12)

则新矩阵∈×2，同样对其进行特征值分解:

(13)

式中：特征值矩阵∈×;酉矩阵∈×,类似于式(7),可以把分为主空间和非主空间:

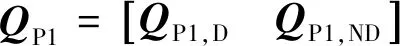
(14)

其中：∈×(+1),∈×(--1)。则新的投影矩阵为

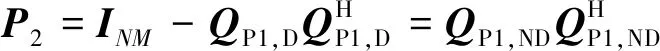
(15)

式中：∈×。则可以构造第2个REC通信波形为

=

(16)

式中：∈、∈与类似为收发方已知的矢量。

按照步骤1和步骤2依次产生个REC通信波形。

2.2 REC接收机设计

现有的REC接收机主要分为3种：匹配滤波器(Matched Filter, MF)、去相关接收机(Decorrelating Filter, DF)和对角加载的去相关(Diagonally Loaded Decorrelating, DLD)接收机。

2.2.1 MF接收机

MF接收机是将接收到的信号和REC波形集中的波形逐个进行匹配滤波，然后将相关性最高的波形视作接收到的波形。其判决公式可表示为

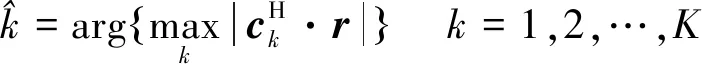
(17)

2.2.2 DF接收机

进一步考虑到在实际中影响MF接收机性能的主要是雷达回波信号对相关判决的干扰，基于最大似然估计理论，设计出了可以去除REC信号和雷达回波信号相关性的DF接收机，其设计原理如下。类似与式(12)，首先将个REC通信波形向量加入矩阵中形成矩阵

(18)

然后生成个去相关滤波器：

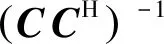
(19)

类似于式(17)，判决表达式为

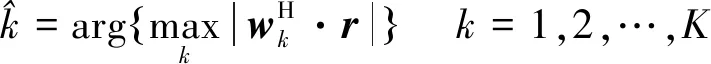
(20)

DF接收机可以有效去除REC通信信号和雷达回波之间的相关性，因此具有更好的判决性能。

2.2.3 DLD接收机

进一步，DLD对去相关滤波器做出如下改进：

(21)

式中:为非主空间中最大的特征值。其判决过程类似：

(22)

DLD接收机性能优于前2种接收机，其对角加载项方便于分析滤波器提供的处理增益，并且能够应对一些不良情况。

3 基于SVD的REC波形设计方法

本节突破基于特征值分解理论进行REC通信波形设计的限制，提出了一种基于SVD理论来提取矩阵特征，进而构建REC通信波形的设计方法。其算法步骤如下：

对进行SVD分解

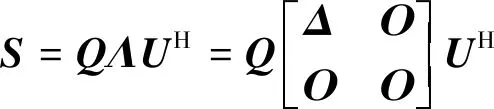
(23)

式中：∈×和∈(2-1)×(2-1)分别为与和的特征值对应的特征向量组成的酉矩阵;∈×(2-1)为奇异值矩阵;=diag(,,…,)为对角阵，≥≥…≥>0为矩阵的个正奇异值;为矩阵的秩。

主空间特征值置零

类似于DP波形生成算法，定义前个较大奇异值对应的特征向量空间为主空间，后-个奇异值对应的特征向量空间为非主空间。为标签和合作接收机共同约定。

将奇异值矩阵中主空间对应的奇异值全部置零，可以得到一个新的矩阵为

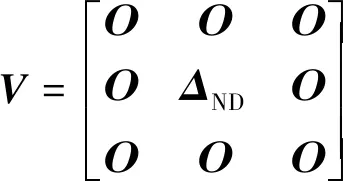
(24)

式中：=diag(+1,+2,…,)为非主空间特征值构成的对角阵。

构造REC生成矩阵

矩阵已经可以被用来构造通信波形，但是为了构造相互正交的通信波形集，需进一步对进行处理生成可以构造正交通信波形的REC生成矩阵。同样假设有个通信波形需要生成，考虑生成个不同的REC生成矩阵，每一个REC生成矩阵为矩阵保留非主空间一部分奇异值、其余奇异值置零所得到的矩阵，保留的奇异值应该遵循下面原则：

每个非主空间奇异值只能被保留一次。后面将会看到，这一条件保证了构造的REC通信波形之间的正交性。

每一个REC生成矩阵都要尽可能选择较大的奇异值。这一条件可以保证每个REC通信波形的性能。

个REC生成矩阵保留的奇异值个数应该相近，并且较大奇异值应均匀分布于各生成矩阵之中。这一条件可以保证每一个REC通信波形相互平衡，进一步保证通信的可靠性。

生成REC通信波形

REC通信波形生成根据

==1,2,…,

(25)

式中：∈为REC通信波形;∈2-1为加权列向量，其由收发方共同约定。

为了与传统REC波形进行区分，把这种基于SVD理论生成的REC波形称为SVD波形。

4 仿真与性能分析

本节对SVD波形的通信可靠性、LPD特性、LPI特性和算法时间复杂度进行分析，并进行相应的仿真实验进行验证。

4.1 SVD波形可靠性分析与仿真

影响REC性能的一个重要方面是REC波形的正交性，REC波形之间的正交性越高，则REC波形之间的相互影响越小，通信可靠性就越高。文献[22]对传统REC波形的正交性进行了分析，并通过添加一定的约束，保证传统REC波形之间具有弱的相关性，但是始终没有办法保证REC波形之间的完全正交，这在一定程度上制约了REC性能的提高。

下面对SVD波形进行正交性分析。考虑任意2个不同的SVD波形和，其中,∈，,≤且≠，对应的REC生成矩阵分别为和。计算和的内积为

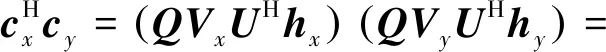
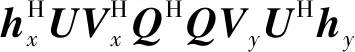
(26)

式中：和为不同的列向量；根据酉矩阵定义有

==

(27)

此外，由第3节步骤3中原则1可以证明：

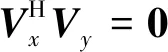
(28)

因此式(26)可以进一步推导为

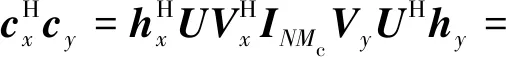
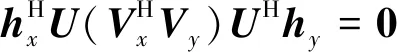
(29)

可以得出结论，SVD波形是完全正交的，这很好地解决了传统WC和DP波形不正交的问题，可以进一步提高通信的可靠性。

下面通过仿真进行验证。假设雷达发射信号为LFM信号，杂波和环境噪声服从高斯分布，合作接收机为DLD接收机。信干比(Signal-to-Interference Ratio, SIR)定义为REC信号和雷达回波信号的功率比，分别设置SIR为-25 dB和-30 dB进行可靠性仿真分析。其他各参数设置为：=100，=2，=100，=4。

图5分别为SIR=-25 dB和SIR=-30 dB功率约束下SVD波形误码率SER和信噪比SNR曲线。可以看到，图5(a)中，SVD波形相较DP波形始终有1 dB左右的SNR增益，与WC波形可靠性能基本相当。图5(b)中，在SER为10时，SVD波形相较DP波形有1 dB左右的SNR增益，而较WC波形有3 dB左右的SNR增益。这些增益可以归因于SVD波形的正交性及SVD波形与雷达回波局部相似性的降低(局部相似性将在4.2节中介绍)，因此SVD波形通信可靠性性能优于传统的WC和DP波形。同时也可以看到，传统EAW波形通信可靠性优于另外3种REC波形，但后面4.3节将会看到，EAW波形并不具有LPI特性，因此EAW波形不可用于REC系统。

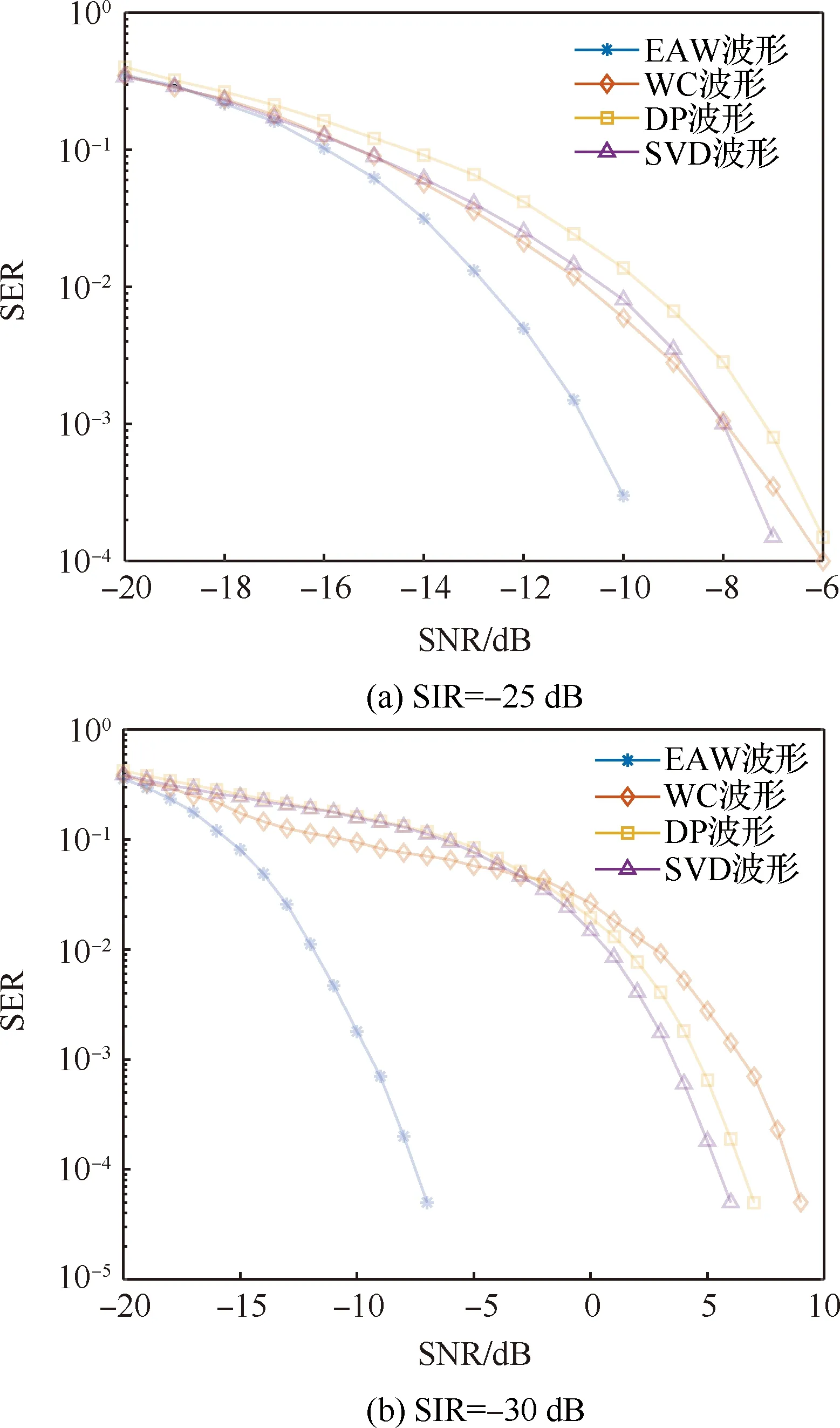
图5 通信可靠性比较Fig.5 Comparison of communication reliability

4.2 LPD性能仿真与相似度计算

与4.1节相同，假设雷达信号为LFM信号，杂波和环境噪声服从高斯分布，参数设置为=100，=2，=100，=4。图6对传统EAW、WC、DP及SVD波形的频谱特性进行了仿真对比，并与雷达回波频谱进行了比较。

从图6可以看到，REC波形功率主要集中在雷达回波过渡带，这样设计的目的是使REC信号避开高功率的雷达通带区域，防止雷达信号对通信的干扰以及通信信号对雷达的干扰。相对于传统3种REC波形，SVD波形与雷达回波频谱在过渡带有着更加相似的变化趋势，截获接收机在截获到含有SVD波形的雷达回波中更难以发现通信信号的存在，其将会更加容易将截获到的信号判定为雷达回波而不是通信信号。另外，看到SVD波形在局部细节上其实与雷达波形相似度有所降低，但实际中SVD波形功率低于雷达回波功率20 dB以上，并受到噪声影响，局部的不相似性并不会在频谱上明显显现，而反过来局部相似性的降低使雷达回波对通信信号的干扰程度降低，会进一步增强通信可靠性。因此相较于传统的REC波形，SVD波形有着更好的LPD特性及通信可靠性。

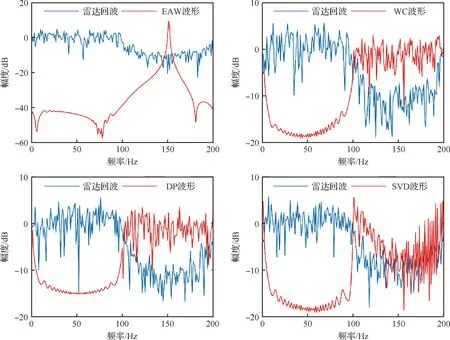
图6 REC波形频谱Fig.6 Spectrum of REC waveform

与基于特征值分解构造REC波形相比，基于SVD进行REC波形构建的另一个优势是可以计算每个SVD波形与雷达波形之间的相似程度。由式(4)、式(23)和式(25)可以看出，雷达回波信号矢量和SVD波形矢量分别为=和对随机矢量的线性变换，因此可以通过计算矩阵和之间的相似度来度量任意一个SVD波形和雷达波形的相似程度。这里采用欧式距离来度量相似度，因此任意一个SVD波形和雷达波形的相似程度定义为

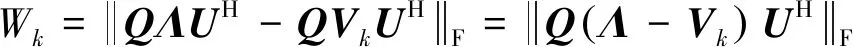
(30)

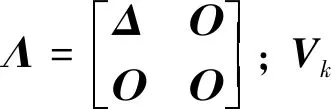
根据矩阵F范数的性质，式(30)可以计算为

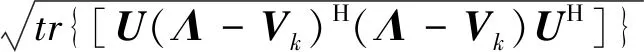
(31)

式中：tr(·)表示矩阵的迹。

根据矩阵迹的性质将式(31)进一步化简为

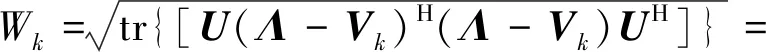
(32)

式中：和都为对角矩阵，相似度可以进一步写为

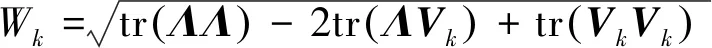
(33)

由于和对角矩阵，因此式(33)计算是简便的。

相似度的量化计算可以为SVD波形带来2个明显的优势：

1) 可以用相似度指标准确衡量LPD特性，的值越小，则代表SVD波形和雷达回波的相似程度越高，波形性能越好。这样LPD特性就不再依赖于人眼来观察频谱，使得LPD特性得以量化，解决了REC系统中LPD特性的分析问题；

2) 通过调整第3节步骤3中所保留的非主空间奇异值，可以灵活控制生成的SVD波形和雷达回波之间的相似程度，从而为可靠性和隐蔽性之间的权衡提供参考。

4.3 LPI性能分析

REC的另一个评价指标是LPI性能。由于REC是在高能量的雷达散射回波之中嵌入通信信号来实现隐蔽通信功能，因此传统的基于信号能量来测量抗截获性能的方法已不再适用。

本文假设截获接收机已知REC的设计原理、雷达信号参数、时宽带宽积以及过采样因子，因此截获接收机可以对雷达信号进行特征值分解，并通过估计主空间大小，将接收向量投影到非主空间来提取整个非主空间波形成分，然后将截获接收机截获到的波形与原始REC波形进行归一化相关度量来评估LPI性能。

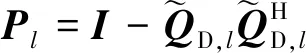
(34)

式中：∈×。用对截获信号进行投影处理可以得到估计的通信波形为

(35)

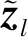
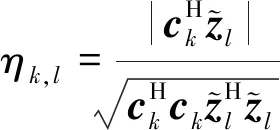
(36)

式中：,∈[0, 1]。虽然归一化相关系数度量不能直接代表截获概率，但其可以有效度量截获接收机提取雷达中通信波形的准确程度，为LPI性能提供有效参考。,值越大，则代表截获接收机估计的REC通信波形准确程度越高，LPI性能越差。

图7对SVD波形的LPI性能进行了仿真，SIR分别设置为-25 dB和-35 dB，SNR设置为-5 dB，其他各参数设置为：=100，=2，=100，=4。通过与EAW、WC和DP波形的对比可以发现，SVD波形的LPI性能优于其他3种波形的LPI性能，这是因为SVD波形与雷达回波的相似程度更高，雷达波形对截获接收机分离通信波形的干扰程度更大，这与4.2节的结论相吻合。

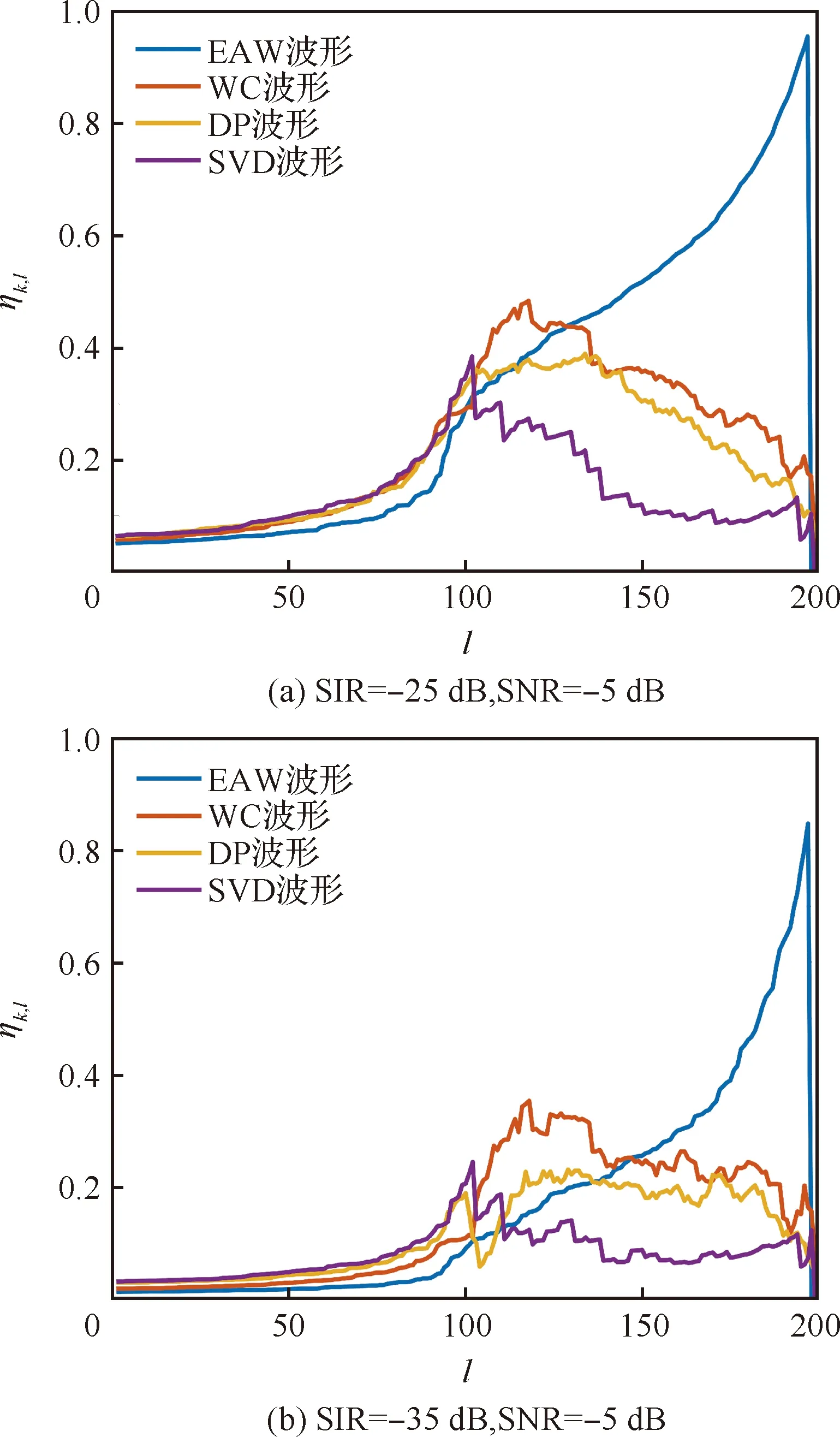
图7 SVD波形LPI特性仿真Fig.7 LPI performance of SVD waveform

通过对比图7(a)和图7(b)还可以发现，SIR越高，LPI曲线包络面积更小，LPI性能越差，这是由于SIR越大，通信信号能量相对越高，被截获的概率也就越大。

4.4 时间复杂度分析

REC波形生成算法的时间复杂度不仅影响RF标签应答系统的复杂程度，而且影响REC系统的响应延迟和嵌入通信信号的时间准确度，进而影响LPD性能。本节对EAW、WC、DP和SVD这4种波形生成算法的时间复杂度进行考量，分析并对比SVD波形生成算法的时间复杂度性能。

对于EAW波形生成算法，其只需要进行一次特征值分解，其算法时间复杂度可以表示为

=(())

(37)

对于WC波形生成算法，其需要进行一次特征值分解并将非主空间矩阵∈×(-)与权值向量∈-进行次相乘，因此其时间复杂度可以计算为

=(()+×(-))=

(()+()-)

(38)

对于DP波形生成算法，其需要进行次特征值分解、由式(10)生成个投影矩阵、并将∈×与随机向量∈进行次相乘，因此其时间复杂度可以计算为

=(()+()+()·

(-))=(2()-())

(39)

对于SVD波形生成算法，其需要进行一次奇异值分解，复杂度为

(×(2-1))=(4())

(40)

式(25)中生成个SVD波形计算复杂度为

(×(2-1)+×2)=

(4())

(41)

因此SVD波形生成算法时间复杂度为

=(4(+1)())

(42)

通常，≫，因此SVD波形算法与传统3种REC波形生成算法在时间复杂度上都为=(())量级，SVD算法并不会过多增加算法复杂度，RF标签依然可以满足算法运算需求。

5 结 论

为了实现更高的通信可靠性和更低的截获概率，本文提出了一种基于SVD的REC波形生成算法，并对SVD波形的性能进行了仿真和分析。通过与传统REC波形的对比发现，SVD波形相较于传统的WC和DP波形具有更可靠的通信性能和更低的截获概率，其高可靠性主要来源于波形之间的正交性，低截获性来源于SVD波形与雷达回波总体的更高相似性。此外，雷达和通信信号频谱局部相似性的降低也有利于减小干扰，提高可靠性。其次，SVD波形和雷达回波之间的相似性可以进行量化计算，从而可以为波形设计提供参考。最后，相较于传统REC波形生成算法，SVD波形方法并没有增加过多算法复杂度，RF标签依然可以满足其运算需求。