延迟高超声速边界层转捩技术研究进展

刘强，涂国华，罗振兵，陈坚强，赵瑞，袁先旭

1. 中国空气动力研究与发展中心 空气动力学国家重点实验室，绵阳 621000 2. 国防科技大学 空天科学学院，长沙 410073 3. 北京理工大学 宇航学院，北京 100081

更高、更快、更远一直是人类不舍的追求，高超声速飞行器的出现与发展，契合了人类的这一诉求。高超声速飞行器技术是21世纪航空航天领域新的制高点，也是众多世界大国的重大战略需求之一。目前，美国、俄罗斯、欧盟等都投入巨资加紧研制，例如美国的空射快速反应武器(ARRW)计划、美澳联合的高超声速国际飞行试验研究(HIFiRE)项目、欧盟的再入飞行器(EXPERT)项目、印度的高超声速技术演示飞行器(HSTDV)项目，俄罗斯宣称已经将“匕首”“锆石”等高超声速导弹列装部队。但是，高超声速飞行器研制过程中面临诸多困难，例如，美国高超声速技术飞行器(HTV-2)在2010年4月和2011年8月2次飞行试验中均失败。HTV-2项目主管Schulz表示：“在马赫数为20的飞行条件下,我们对飞行器的空气动力学现象还存在认识上的盲区”。边界层转捩及湍流问题就是高超声速领域不可避免的盲区之一，导致了诸如HTV-2飞行试验失败、哥伦比亚号航天飞机失事等重大事故。

边界层转捩通常是指边界层流动由层流状态发展为湍流状态的过程，是一个多因素耦合影响的强非线性复杂流动物理现象。转捩问题是经典力学遗留的少数基础科学问题之一，与湍流问题一起被称为“百年(或世纪)难题”。由于高超声速飞行器的高度、速度和雷诺数范围内恰好非常容易出现边界层转捩现象，因而高超声速边界层转捩问题一直是制约飞行器设计的关键基础问题，也是各航空航天大国当前极为关注的重点研究课题。美国国家高超声速基础研究计划(NHFRP)中明确将高超声速边界层控制列入中、长期重点计划中。美国空军科学研究办公室(AROSR)专门发起了高超声速边界层转捩飞行试验项目(BOLT)。美国国家航空航天局(NASA)“CFD 2030远景”更是把转捩列为第一类急需解决的物理模型问题。中国工程院战略咨询中心发布的《全球工程前沿2019》和《全球工程前沿2020》连续两年分别将“超声速流中的减阻降热研究”和“高超声速飞行器热防护技术”排在机械与运载工程领域工程开发前沿的第3位和第8位。2020年国家自然科学基金委将“高速流动及控制的机理和方法”作为数理学部优先发展领域之一，并把“与高速空天飞行器和海洋航行器流动以及多相复杂流动相关的湍流机理及其控制手段”作为主要研究方向。

高超声速情况下，湍流边界层的壁面摩阻与壁面热流通常3～5倍于层流边界层，精确预测和控制边界层转捩具有非常重要的工程意义。已有研究表明，全层流与全湍流的热防护系统的重量可相差4倍左右，全层流的总阻力可比全湍流降低30%左右，全层流有效载荷是全湍流的2倍。可见延迟高超声速边界层转捩可以有效降热减阻，确保高超声速飞行器“载得更多，飞得更远、更安全”。

针对高超声速边界层转捩，国内外已有不少文章进行了综述。Schneider主要综述了近年来在静风洞获得的试验结果。罗纪生介绍了可压缩边界层流动不稳定性特征、转捩机理与感受性，并着重介绍了转捩预测中的e方法以及所存在的困难。陈坚强团队主要介绍了高超声速边界层转捩的整体研究现状以及针对一些热点问题提出了自己的观点认识。杨武兵团队就转捩机理、预测方法和试验方法进行了综述并给出了相应的研究建议。苏彩虹主要针对转捩过程的一“头”一“尾”，即感受性和转捩判据，重点关注的是圆锥边界层和横流转捩，介绍了相应的最新研究进展及尚且存在的问题。李存标团队基于静风洞试验(包括近壁Particle Image Velocimetry(PIV)、CO瑞利散射等流场测量技术)、Direct Numerical Simulation(DNS)和稳定性分析等，在高超声速边界层转捩机理探索与转捩延迟控制方面取得了系列进展，比如其系统研究了转捩过程中第二模态在气动加热中的作用机制，给出了气动加热和气动降热的准则，揭示出压力脉动和速度胀量之间的相位关系决定了其做功表现为气动加热还是气动降热，并通过控制模型表面声阻抗，将表面热流降低了28%。易仕和团队介绍了基于纳米示踪的平面激光散射(NPLS)技术在高超声速边界层转捩中的应用。段毅等回顾了具有复杂外形的飞行器存在的典型失稳特征，提出了工程中亟需解决的问题。但是，全面系统论述边界层转捩控制的文献相对较少。李志文等从飞行器总体设计角度进行了分析，发现若能对高超声速边界层转捩过程进行延迟控制，在高超声速飞行器的减阻、表面热防护与气动外形优化等方面都具有极高的应用价值，这已成为当前高超声速飞行器工程设计与可压缩流体力学领域研究的热点问题。

得益于以上文献的启发，本文着重介绍高超声速边界层转捩延迟控制技术的最新研究进展，从被动控制和主动控制的角度介绍各种转捩延迟控制技术，并介绍转捩控制背后的物理机制，最后对转捩延迟控制技术的下一步研究进行展望。

1 高超声速边界层转捩及其控制概述

边界层转捩伴随着高超声速飞行器的发展，从20世纪50年代起就一直是研究人员重点关注的问题。一般认为，转捩是由流动中的扰动失稳引起的。在高超声速技术领域，人们认识到在小扰动作用下边界层存在4类流动失稳机制，分别是：流向行波不稳定性、横流不稳定性、Görtler不稳定性与附着线不稳定性。不同失稳机制主导的边界层流动需要采取不同的控制措施。

流向行波失稳即通常所说的T-S波引起的流动失稳，是目前理论研究最多也是最为透彻的一种失稳机制。Mack研究指出，当边界层来流马赫数大于2.2时流动中同时存在具有不同波数和相速度的多种不稳定扰动波。Mack根据波数由低到高将这些扰动波分别称为扰动第一模态、第二模态等，其中第一模态即对应低速情形的T-S扰动波，而第二模态及其以上模态由于具有声辐射特征，因而又称为“声模态”。当来流马赫数超过4之后，第二模态扰动将成为最不稳定扰动波。图1(a)给出了高超声速边界层中的声学模态示意图(图中()为平均速度型；()为压力扰动型函数；为当地声速；为扰动相速度)，可以将边界层看成一个声波导管，第二模态及其高阶谐波等声波扰动在壁面和声速线之间不断反射并向前传播，在传播方向上由一系列交替呈现的压缩区域和膨胀区域组成，其密度和温度分布形态上呈现“绳索”状分布(图1(b))。横流不稳定性常见于三维边界层，如后掠翼、椭圆锥和有攻角圆锥等的边界层。三维边界层通常存在垂直于势流方向(横向)的压力梯度，使得边界层内出现垂直于势流方向的速度分量，即所谓的横流。横流速度剖面存在广义拐点，易发生无黏失稳，导致横流驻波或横流行波，其在一定条件下发生二次失稳，最终导致转捩。徐国亮和符松对可压缩横流失稳及控制进行了系统介绍。Görtler不稳定性是由于离心力和法向压力梯度的不平衡造成的，常存在于凹曲面流动。Görtler不稳定性易导致Görtler涡，其流场特征是一对对反向旋转的流向涡以及高低速条带结构，Görtler涡容易发生二次失稳并导致转捩。任杰和陈曦对高超声速情况下的Görtler涡稳定性及控制进行了较为全面的介绍。附着线不稳定性通常发生在飞行器的前缘附着流线上，如机翼前缘附着线。陈坚强等在对高超声速边界层转捩研究标模HyTRV的边界层进行稳定性分析时证明，高超声速前缘附着线失稳的本质是第二模态失稳。

图1 高超声速边界层中的声学模态示意图和试验观测图Fig.1 Schematic diagram of acoustic modes in hypersonic boundary layer and experimental observation

2 高超声速边界层转捩延迟控制手段

2.1 粗糙元与有限幅值条带控制

粗糙元应用于高超声速边界层转捩控制从20世纪50年代就已开始。粗糙元可以分为两种类型，即孤立式(Isolated)和分布式(Distributed)。高度与位置是粗糙元控制的重要敏感参数，不同位置不同高度的粗糙元，对边界层的转捩控制效果可能截然相反。粗糙元在转捩促进中的研究较为常见，Schneider针对转捩促进开展了大量的工作，但在转捩抑制中的研究并不多。最早在风洞试验中发现粗糙元抑制转捩现象的是Sterrett和Holloway，在孤立粗糙元的高度为当地边界层的0.76和1.26倍时，他们观察到了边界层转捩被延迟的现象，并认为这是粗糙元附近层流分离区导致的。在随后的风洞试验中，发现在平板上安装一个半球形粗糙元也能将转捩位置往下游推移。

Fedorov基于稳定性理论研究了高超声速边界层中声扰动被二维粗糙元散射引起的感受性问题，发现二维粗糙元的流向位置是第二模态波受何种影响的关键，当二维粗糙元布置于慢模态及快模态相互作用的同步点附近时，相应第二模态波的振幅最强。Marxen等则发现二维粗糙元对不同频率范围的第二模态波会产生不一样的影响，对某些频率的扰动能够放大，对某些频率的扰动能够抑制。他们认为粗糙元的作用其实相当于一个“低频放大器”。Zhong等的研究发现，当粗糙元布置于慢模态及快模态相互作用的分支点上游时，第二模态波几乎不受粗糙元影响。当粗糙元布置于分支点附近或下游时，第二模态波的振幅会被二维粗糙元所抑制。Fong等也发现粗糙元和边界层内快模态与慢模态同步点的相对位置对扰动波的发展非常关键，如果粗糙元安装在共振点之后(前)，那么会抑制(放大)慢模态。李慧对马赫数为4.5、飞行高度为30 km、有鼓包的平板边界层中扰动的演化进行了研究，发现粗糙元对一些频率的扰动起促进增长作用，而对另一些频率的扰动起抑制作用。总之，粗糙元对扰动波的影响取决于安装位置：在给定扰动波频率的情况下，安装在共振点之前的粗糙元对第二模态的影响有限或有促进作用；若安装在共振点之后，则对第二模态有抑制作用；若安装在共振点附近，则易激发第二模态；由于不同频率扰动波的共振点不相同，在给定粗糙元安装位置的情况下，低于安装位置处共振频率的扰动波将会被放大，高于共振频率的扰动波将会被抑制。

通过合理布置粗糙元来激发有限幅值的条带在转捩抑制方面也逐渐引起重视。有限幅值条带延迟转捩的机理在于条带对边界层的修正作用使得边界层更加饱满，流动更加稳定，但其控制前提是条带的强度不能超过二次失稳的临界强度。Fransson等在2006年的风洞试验中，利用展向等间距分布的粗糙微元来产生条带结构，抑制边界层中T-S波的增长，实现了转捩的延迟。Ren等在马赫数=4.5和=6条件下考察了K型条带和G型条带与边界层内二维扰动波的相互作用，当条带幅值在合适范围内时(也就是足以调控边界层而又不引发二次失稳)，第一模态和第二模态都会被抑制。Paredes等在=5.3条件下采用PSE(Parabolized Stability Equations)研究了粗糙元对7°半锥角圆锥边界层的转捩控制，在他们的试验中，单组粗糙元带来了17%的转捩延迟效果，而若使用两组粗糙元来交替控制(即采用后者来抑制前一组粗糙元自身诱导的不稳定性)，更是能够取得40%的延迟控制效果。

条带同样可以用于抑制三维后掠翼边界层的横流失稳。Rizzetta等采用DNS和NPSE(Nonlinear Parabolized Stability Equations)计算了Saric等的飞行试验结果，分析了机翼前缘方形、圆柱、鼓包等粗糙元构型对横流转捩的影响，取得了良好的横流抑制效果。Schuele等在=3.5条件下研究了小攻角圆锥边界层的转捩情况，当采用亚临界间距的粗糙元激发次不稳定定常横流涡，边界层流动内部扰动减小，转捩位置可以推迟35%。Corke等进一步将Schuele等的试验拓展到了=6来流条件下，依然取得了25%的转捩延迟控制效果。然而，Owens等采用粗糙元进行超声速后掠翼边界层转捩延迟控制的效果却并不明显。粗糙元和条带控制横流转捩的主要机理是生成相对稳定流向涡，调节边界层型面，避免最不稳定或危险的横流涡产生，从而延迟横流转捩。但是，粗糙元的控制效果对流动参数非常敏感，比如Carpenter在30°后掠翼的112次飞行试验中仅有6次观察到了边界层转捩被明显推迟的现象，不适当的流体条件下很可能导致转捩提前，可见粗糙元和条带控制从风洞试验走向实际飞行仍然还面临许多挑战。

2.2 波纹壁

诸多高马赫数下的混合层和尾迹流动数值和试验研究表明，马赫数的增加会对边界层产生稳定作用，剪切不稳定作用也会被抑制，这就引导人们探索研究局部边界层分离对第二模态的影响。Fujii最早开展了波纹壁对转捩的抑制研究试验，其通过在5°半锥角的尖锥表面失稳区域上游2倍边界层厚度的范围布置波纹壁，在自由来流高总温(970 K)的条件下,当波纹壁的波长与第二模态波的波长相当时，转捩被有效推迟。据此推测，当波纹壁的波长和第二模态的波长之间符合某种特定的关系时，波纹壁有可能延迟边界层转捩。Egorov等在=5.9条件下开展了波纹壁延迟高超声速平板边界层转捩的直接数值模拟研究，在上游通过高频激励激发第二模态不稳定波，图2给出了平板表面(上)与波纹壁表面(下)的脉动压力(′/)对比图，在离散分布的分离区中，边界层表现出了混合层的特性，不稳定波在一定程度上被抑制。但Bountin等认为波纹壁的延迟控制效果主要是其对基本流的修正，而不是直接作用于第二模态。Zhou等考察了波纹数目、深度、流向位置等几何构型对转捩位置的影响，发现随着波纹深度/数目的增加，对不稳定波的抑制作用更明显；当波纹壁布置在下游时，对第二模态的抑制作用也更明显。Si等在北京大学=6静风洞中研究了不同雷诺数下波纹壁面对高超声速裙锥边界层转捩及其气动热的影响，也证实波纹壁面能够在一定程度上抑制第二模态的不稳定作用，并延迟转捩的发生，同时，波纹壁也完全抹去了气动加热的第一个热流峰值。

图2 平板表面(上)与波纹壁表面(下)的脉动压力对比[58]Fig.2 Comparison of fluctuating pressure on flat plate(upper) and wavy wall(lower)[58]

但设计好的波纹壁可能仅对特定频率范围的不稳定波有抑制作用，对较低频率的扰动可能存在一定的失稳作用。Bountin等的研究发现，在所给定的试验条件下，波纹壁使得频率超过110 kHz的扰动幅值衰减，但较低频率范围(80～100 kHz)的扰动却被放大。可见，还需要进一步研究波纹壁对各种扰动的影响特性或有效工作范围。

2.3 微孔隙表面

在被动式转捩延迟控制手段方面，研究最广的莫过于微孔隙表面。超声波吸收表面(Ultrasonically Absorptive Coating, UAC)是一种非常典型的微孔隙材料，它是由规则或随机分布的微腔构成的薄层，进入微腔内的声学扰动引起内部空气的剧烈运动，在黏性耗散作用下，声学扰动的部分机械能转化为热能。另外，流动中有声学扰动经过时，会产生压缩和膨胀的变化，压缩区温度升高，膨胀区温度降低，相邻压缩区和膨胀区之间的温度梯度会导致热量从温度高的部分向温度低的部分发生热传导。这个过程是不可逆的，声学扰动的部分机械能也会转化为热能。因此在黏性耗散和热传导的共同作用下，第二模态波的机械能转化为热能，第二模态不稳定波受到抑制(见图3(a))，进而延迟边界层转捩。

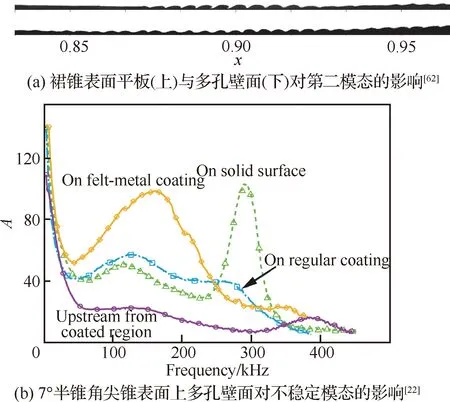
图3 多孔壁面对不稳定模态的影响Fig.3 Effect of porous coating on unstable modes

1998年，Malmuth等最早指出使用吸收高频声波的多孔表面能够有效抑制第二模态的增长。通过在一个波长内布置15～20个深孔，Fedorov等率先开展线性稳定性分析(Linear Stability Theory, LST)并在尖锥边界层上予以风洞试验证实。此外，Fedorov等提出的模化多孔表面的阻抗边界模型奠定了后人研究的基础。但Fedorov的研究也发现，多孔表面控制尽管抑制了第二模态的不稳定作用，却也带来了低频扰动被激发的现象(见图3(b)，图中为扰动谱能量)。

Chokani等采用相干谱分析发现，相对于固体壁面，多孔表面改变了第二模态波的谐波与次谐波共振特性，多孔表面上的谐波共振现象消失，非线性相互作用增强，并且这种非线性作用与第一模态的失稳紧密相关。Sandham等采用时域直接数值模拟方法(流向设置周期边界)对多孔表面延迟转捩进行了研究，结果显示多孔表面能够有效抑制第二模态不稳定波的发展，并降低二次失稳波的增长率，同时指出DNS求解的扰动增长率要低于LST理论预测结果。Brès和Tritarelli等发现多孔表面能够减小第二模态的能量，但也使得第一模态发生了轻微失稳。Zhong团队采用理论和数值计算对高超声速边界层转捩机理及其流动控制进行了大量研究，发现多孔表面对第二模态波的影响与多孔层的位置有关：当多孔表面位于同步点上游位置时，会促进第二模态波的发展，而当多孔表面位于同步点下游位置时，对第二模态波有稳定作用。Lukashevich等采用风洞试验研究了覆盖层的长度、位置对第二模态的影响，发现若覆盖层位于扰动模态同步点之前时，反而会放大第二模态的增长率。Sousa等采用时域阻抗边界来模化宽频带范围内声波在多孔表面的传播特性，并尝试开展全转捩过程DNS模拟，但由于数值格式鲁棒性太差导致DNS的计算发散，并且其模型也没有考虑到多孔表面的热黏性效应。Fievet等同样基于时域阻抗边界，采用高阶谱差分求解器对单频扰动下多孔表面响应进行了数值模拟，获得与LST一致的结果。

另一方面，为进一步模拟高超声速飞行器防热层使用的防热材料，Fedorov等通过风洞试验和LST证实了金属毡对第二模态的抑制效果。Maslov、Wang和Zhang分别采用风洞试验与数值模拟手段，对比了规则孔隙表面与金属毡对第一模态/第二模态的作用效果，结果显示规则孔隙表面对第二模态的抑制效果弱于金属毡，但对第一模态的激发效应也要小于金属毡。自2013 年起，德国宇航局开始对实际热防护系统所用到的碳纤维增强碳材料(C/C)开展抑制高超声速转捩研究。Wagner等在高焓激波风洞验证了C/C材料对高超声速边界层(=7.5)转捩的抑制效果，并发现抑制效率与来流雷诺数有关。各团队所采用的试验模型如图4所示。

图4 风洞试验模型Fig.4 Wind tunnel test models

近年来，国内针对多孔表面延迟转捩也做了大量的研究。朱德华等采用DNS和基于阻抗边界的LST方法比较了三维顺排和三维错排的矩形微孔对不稳定波的影响，研究表明两者都可以抑制第二模态扰动的发展，但是顺排多孔表面延迟高超声速边界层转捩能力更强。涂国华等利用LST分析了不同开孔率和孔半径对第二模态扰动波的影响，得到了抑制扰动波幅值增长的最优开孔率和孔半径。Zhao等考虑孔隙表面微结构之间的声学干扰，重新推导了规则孔隙表面(微缝隙/圆孔/方孔)的作用机理模型，提高了对孔隙表面声学特性的预测精度，并提出一种数值优化设计方法，可得到单频最优吸声效果下的微结构几何参数；他们还分别研究了表面阻抗相位对第一模态/第二模态的抑制作用，设计了一种不明显激发第一模态的前提下有效抑制第二模态的多孔表面。Zhao等引入声学超表面的概念，强调多孔表面人为设计与交叉学科的重要性，并且提出一种近零阻抗的多孔表面。与之前通过微腔黏性耗散声波的机理不同，近零阻抗超表面通过使入射声波与反射声波在壁面处相位相反，声压相互抵消，破坏第二模态的演化形态，同样达到抑制第二模态的目的。最近，赵瑞等系统研究了声学超表面导纳幅值与相位对第一模态的影响规律，并在马赫数为4的平板边界层流动中抑制了第一模态。Zhu等采用风洞试验和稳定性分析相结合的方法研究了多孔表面上高频模态和低频模态之间的非线性相互作用，发现多孔表面对近壁区扰动的抑制改变了基频共振扰动的空间分布特征，打破了锁相关系，抑制了基频斜波失稳，同时研究也发现多孔表面极大地抑制了气动加热并推迟了转捩位置。

上述微孔隙表面的空隙大小通常是微米量级，其加工难度较大。郭启龙等考察了较大尺寸(0.1 mm)横向微槽道，发现其对第二模态有非常强的抑制作用。郭启龙等还分析了横向微槽道对基本流的影响，发现微槽有利于减小壁面摩擦阻力，而压差阻力仅轻微增加，由于表面上的压差阻力要比摩阻小1～2个数量级，所以总阻力减小(见图5,图中为开槽率)。

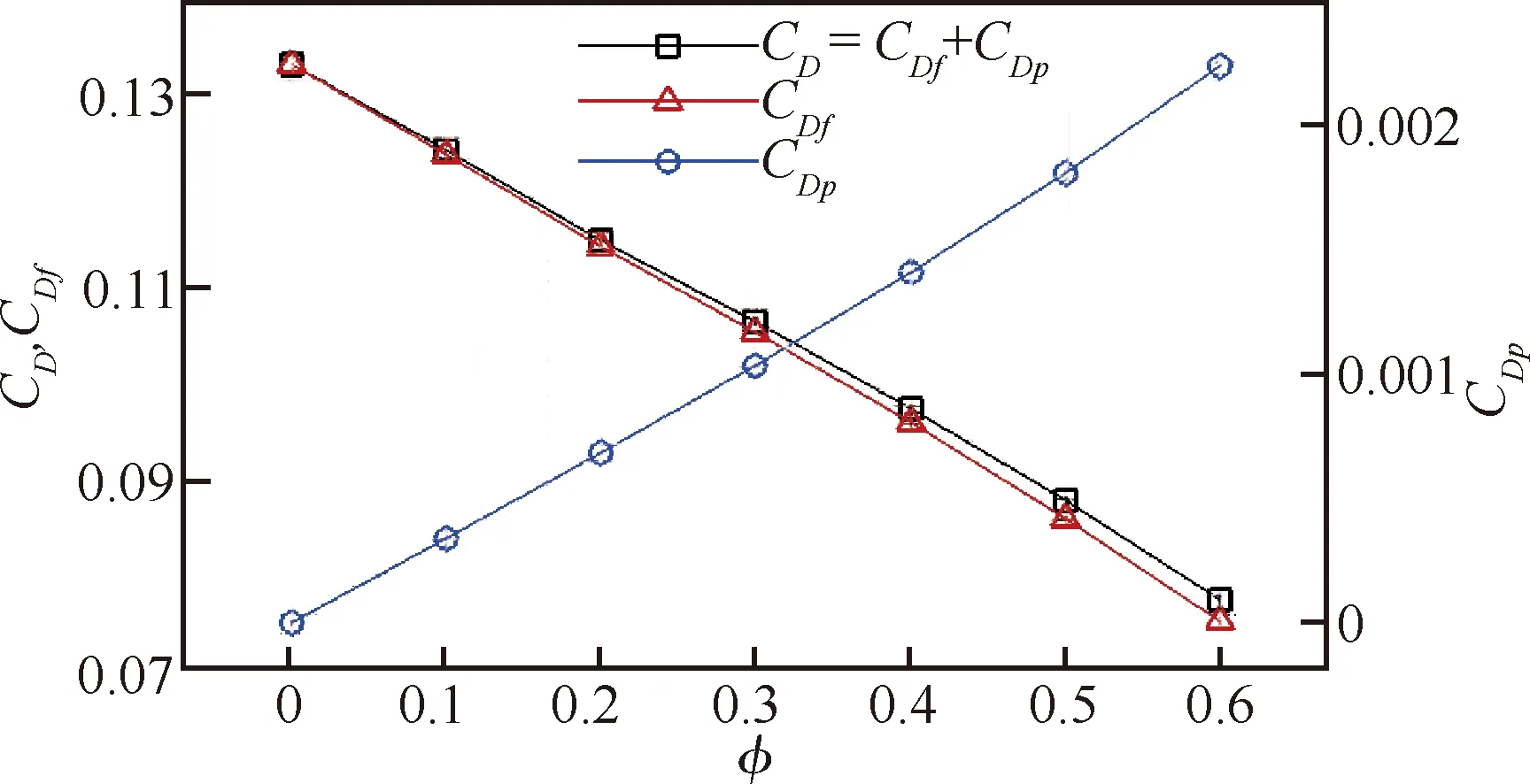
图5 不同开槽率下的摩擦阻力系数CDf、压差阻力系数CDp和总阻力系数CD[88]Fig.5 Friction resistance coefficient CDf,, differential pressure resistance coefficient CDp and total resistance coefficient CD with different porosities[88]

综合微孔隙表面的相关研究成果可以发现，只要安装位置得当，微孔隙表面基本上都有抑制第二模态扰动波的作用，但这种抑制效果对频率具有一定依赖性，对高频第二模态波的抑制效果总体上要优于低频第二模态波。微孔隙也有不利的一面，即对第一模态(或低频模态)具有一定的促进作用。以上结论都是基于风洞试验、DNS或LST得到的，其中部分DNS和LST采用的不是真实边界条件，而是模化后的边界条件，有关真实飞行条件下微孔隙表面能否延迟边界层转捩仍需进一步研究。

2.4 壁面(局部)加热/冷却控制

早在20世纪70年代研究人员就发现，通过降低壁面温度，可以抑制边界层的热耗散率，调节边界层内外层流体之间的交换，进而抑制转捩的发生。事实上，壁面加热或者冷却会引起边界层厚度发生变化，相应的声速线位置也会发生改变，这就将会带来边界层内扰动波(快、慢模态)相速度演化的变化，同步点发生迁移，达到控制流动稳定性的目的。根据稳定性分析结论，冷壁会使得第一模态更稳定而第二模态更不稳定。这个结论事实上是壁温作用于边界层平均剖面的结果，以第一模态为例，由于其失稳的本质原因在于边界层剖面内的广义拐点，当壁面得到足够的冷却时甚至会消除广义拐点。赵耕夫研究了壁面冷却对三维可压缩边界层稳定性的影响，指出壁面冷却虽然能够推迟边界层转捩，但是与二维边界层相比，其层流控制作用是很有限的。

实际情况下高超飞行器的热防护系统由不同导热性能的材料组成，因此其表面总是有不均匀的热流分布。这就促使研究者探索这种局部加热/冷却对高超边界层转捩的影响。局部加热/冷却用于转捩延迟控制最早是在亚声速边界层流动中，取得了较好的控制效果。Soudakov等通过在=6尖锥表面放置局部的加热/冷却单元，发现局部加热/冷却同样能够取得较好的转捩控制效果：局部的冷却会导致转捩推迟，而局部的加热会使转捩更早发生。Fedorov等的风洞试验研究也表明，局部冷却可以抑制第二模态的幅值，延迟转捩的发生。Zhao等针对不同流向位置的局部壁面加热或者冷却对高超声速边界层的影响进行了直接数值模拟和线性稳定性分析，研究发现局部壁面加热的作用机理与粗糙元类似，位于同步点上游时，会放大慢模态，位于下游时则是衰减作用；局部壁面冷却位于同步点上游时能够稳定第二模态，位于下游时，则会产生第二同步点，重新发展的扰动会更强。

Fedorov等还对局部体积能量输入影响高超声速平板边界层流动稳定性进行了二维直接数值模拟和线性稳定性分析，研究发现控制效果取决于能量输入距离前缘的流向位置和法向高度，当能量源位于中性点的上游、中心位置靠近边界层外缘时，能够减小第二模态的增长率、降低不稳定模态的幅值；而当能量源位于下游并且位于边界层以内时，这种稳定作用变得微弱；在中性点附近变换能量源的法向位置发现，稳定效果最好的位置位于临界层(第二模态波的相速度等于平均流的速度)。Fedorov等认为作用机制有两个：① 能量源导致下游第二模态增长率减小；② 不稳定波到达能量源临近区域时被分散，导致不稳定波幅值发生了变化。

2.5 重气体喷注法

重气体延迟转捩法最早源于Germain与Adam和Hornung在风洞试验中的意外发现，他们发现，当试验气体为CO时，边界层的转捩位置被大大推迟。同时，在一定的高温/高焓条件下，随着来流CO浓度的增加，转捩推迟也会更加显著。这是由于高超声速边界层转捩通常是第二模态占据主导作用，而第二模态是一种声波扰动，流动中的非平衡效应能够使得这些声波扰动衰减。

但是从实际应用的角度出发，若要利用CO的特性来推迟高超声速边界层转捩，如何在实际飞行中的来流空气中引入CO是一个难题。有研究人员探索了从壁面直接向边界层内注入CO的方式用于推迟边界层转捩。Leyva等在5°半锥角的尖锥表面开展了基于CO壁面喷注的高超声速边界层转捩延迟控制数值和试验研究，与纯N来流相比，在CO摩尔分数占比为40%的情况下，转捩雷诺数增加超过一倍；数值模拟发现，在喷注(声速射流)区域下游，CO的温度能够达到2 000 K，在此温度下，足以激发CO的4种离解模态中的3种，这将有助于边界层的流动稳定性。Jewell等则对比了空气来流、CO来流，空气/CO占比各半的混合物来流下的转捩控制试验。他们发现，对于混合物来流，转捩的流向位置向下移动了30%；并且，来流的焓值越高，转捩位置越靠后。CO控制的本质是分子的振动与离解将能够吸收掉大部分的第二模态频率附近的能量，从而达到抑制转捩的目的，所以当边界层温度大于CO振动能激发温度时，控制效果较佳。需要注意的是，CO气体的注入也会带来扰动，需要平衡气体注入引入的扰动与CO的稳定效果之间的关系。

重气体对第一模态扰动波也有一定的抑制作用。Gaponov等通过多孔壁面吹气重气体(CCl, SF)，发现其延迟了=2的边界层转捩。重气体边界层的控制效果类似于壁面冷却，增加了边界层的平均密度，第一模态扰动波的放大率降低，提高了边界层的稳定性。

2.6 其他控制方法

其他还有一些转捩控制手段，例如合成双射流、介质阻挡放电、壁面吸吹气与多孔壁面组合、壁面冷却与多孔壁面组合等。周期性的低频合成双射流能够有效修正边界层的剖面，抑制了第一模态不稳定性，但也在一定程度上放大了第二模态不稳定性。对于壁面吸吹气控制，研究发现边界层内非稳态吹吸气能够调节边界层形状和流体的运动，修正边界层的速度剖面。壁面吸气法通过减小边界层厚度、增加边界剖面的饱和度、消除或减弱边界层速度剖面拐点、达到增强稳定性和延迟转捩的目的。同时，Wang和Lallande也研究了稳态的吹吸对高超声速边界层转捩的影响，线性稳定性分析发现，当布置于同步点的上游时，凹形(Concave-type)的壁面稳态吸吹气控制能够稳定慢模态；当布置于同步点的下游时，凸形(Convex-type)的壁面稳态吸吹气控制能够稳定慢模态。Wang等的研究发现，布置于横流涡下的介质阻挡放电能够衰减横流首次失稳的增长率、削弱横流涡，最高实现了扰动能量降低2个量级，在横流转捩抑制显示出一定潜力。

事实上，采用单种控制技术常常存在很大的局限性，采用多种手段组合的方式同时来对边界层内的一种或多种不稳定波进行控制往往能够取得更好的控制效果，这也是当前研究的热点。Fedorov等曾通过多孔壁面喷注CO气体来对第二模态进行控制，多孔壁面从喷注位置一直布置到下游，研究结果如图6所示，施加组合控制以后，上游由于气体喷注带来的值局部峰值因为多孔壁面的存在而减小近一倍，下游区域多孔壁面与CO的组合更是将值由原来的12.5衰减到了3左右，显示出惊人的控制效果。由于多孔表面对第二模态起抑制作用，而壁面冷却对第一模态有稳定作用。基于此，Kudryavtsev和Khotyanovsky提出了冷多孔壁面控制方式，线性稳定性分析结果显示，施加组合控制以后，第一模态不稳定波消失，第二模态不稳定波的增长率也大幅衰减。

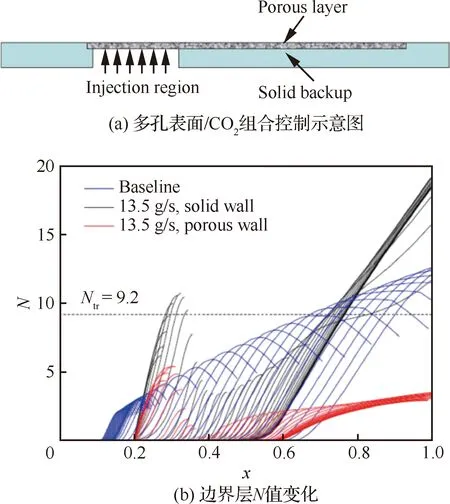
图6 多孔表面/CO2组合控制下的边界层N值变化对比[102]Fig.6 Comparison of N value changes in boundary layer under combined control of porous wall and CO2[102]

3 结论与展望

高超声速边界层转捩会引起壁面摩阻与热流急剧增加，对高超声速飞行器的气动性能和热防护系统具有很大的影响，开展高超声速边界层转捩延迟控制技术研究不仅是流体力学的前沿热点问题，也是国家重大工程亟需的关键技术之一。

相比于低速边界层，高超声速边界层中通常存在第二模态扰动波，因此，当前主流的转捩延迟控制技术大多是针对具有声辐射特性的第二模态开展，而控制第一模态和横流模态的研究相对较少。本文较为全面地介绍了粗糙元、波纹壁、微孔隙、壁面加热/冷却、重气体喷注和一些混合控制方法。

粗糙元可用来抑制第二模态扰动波，但其安装位置和高度对控制效果非常关键，需要预先知道快/慢模态的同步点位置。由于不同流动参数和不同扰动频率下的同步点位置很可能不同，所以还需要通过研究来明确粗糙元抑制第二模态扰动波的有效工作范围。粗糙元也可被用于激发有限幅值条带来抑制转捩，但前提是条带的强度必须小于其发生二次失稳的临界强度，这一点对粗糙元的设计提出了更高的要求。同时，粗糙元也在一定程度上带来了附加阻力与附加热流，不得不考虑额外的热防护设计。

微孔隙表面在不明显影响主流的情况下，通过吸声和黏性耗散机制有效抑制了第二模态的发展，是最可能投入工程实践的技术，但多孔表面也可能带来低频模态的失稳。

壁面温控技术利用边界层厚度与声速线位置的变化，调节不稳定波的频率等特性。这种控制技术原理上比较简单，但高效控制的背后却需要巨大的能量消耗，这种能量消耗对于高超声速飞行器有限的机载能源来说是个巨大的挑战。

CO等重气体喷注法利用的是重气体的分子振动和高温离解来吸收耗散声波的能量，但振动激发通常在800 K以上才比较明显，风洞试验原则上应该在高焓风洞中开展，且若想取得较好控制效果，需要注入大量二氧化碳。壁面吸吹气控制若不当，可能产生小激波、声波或其他扰动。

当前高超声速边界层转捩延迟控制技术多是针对第二模态失稳，少部分涉及到横流失稳和第一模态失稳。然而，随着高超声速飞行器外形越来越复杂，边界层中常常同时存在横流失稳、流向涡失稳、第二模态、附着线失稳等多种不稳定模态。因此，发展能够抑制多种不稳定模态的转捩控制技术将会是未来研究的热点之一，当然，也是难点。

由于单一控制手段的有效工作范围有限，难以满足下一代高超声速飞行器大空域、宽速域的飞行要求。未来的研究可以考虑多种控制手段相结合，比如利用微孔隙壁面与壁面冷却组合控制第一和第二模态，利用微孔隙壁面与微吹吸组合控制第一、第二和横流模态，利用烧蚀产生CO，利用介质阻挡放电或射流产生“等效粗糙元”等。另外，还需适当考虑各种控制手段对感受性和瞬态增长的影响，目前这方面的研究相对较少。

总之，下一代高超声速飞行器的气动及热防护设计，很大程度上取决于对转捩机理的认知深度及对其的控制能力，即取决于对“转捩时间、转捩位置、转捩方式、转捩控制”4个问题的解决程度。就延迟转捩控制而言，发展低热、低阻、低能耗的控制手段的道路依然漫长。

致 谢

感谢空气动力学国家重点实验室张毅锋、郭启龙、陈曦、万兵兵、李晓虎等同事的有益讨论与帮助。