一种涵道螺旋桨桨叶高效设计方法
2022-09-05郭佳豪周洲李旭
郭佳豪,周洲,李旭
西北工业大学 航空学院,西安 710072
涵道螺旋桨,即螺旋桨外部包围涵道的一种动力形式,被广泛应用于航空和航海领域,为飞行器、舰船、潜艇等提供动力。相比孤立螺旋桨,涵道螺旋桨具有更高的安全性以及气动效率,因此研究高效的涵道螺旋桨设计方法具有较高的工程应用价值。
涵道螺旋桨设计方法一般基于叶素动量理论、升力线及面元法等快速方法,常用于涵道螺旋桨的初始设计。国外方面,Coney采用环涡与对称涡模型等效涵道,并基于升力线模型,提出一种涵道螺旋桨设计方法。Stubblefield应用Kerwin最优环量求解方法螺对涵道旋桨进行了详细的设计。此外,Epps和Kimball对螺旋桨升力线设计方法进行了研究,并提出一种新的螺旋桨尾涡模型,与经典尾涡模型的对比表明其具有较好的精度,并且鲁棒性更高。基于以上研究,Epps等开发了OpenProp螺旋桨设计软件,并将涵道螺旋桨设计方法集成其中。
国内方面,刘沛清推导了涵道螺旋桨叶素动量理论。高永卫等提出一种涵道螺旋桨工程设计方法,并根据轴流风机叶素理论进行桨叶设计。宋长红等建立了基于动量源方法的涵道尾桨数值模拟方法,通过对比试验结果验证了方法的可行性。叶坤等通过动量源方法简化桨叶,分别采用响应面模型和神经网络模型,对NASA涵道进行优化设计。姬乐强等采用动量源方法,研究了唇口半径、涵道扩张角、桨尖间隙及桨叶相对位置等涵道参数对整体气动力的影响,并对涵道外形进行了优化设计。此外,杜思亮等对一种开口壁式涵道螺旋桨进行了研究,并提出一种嵌入式涵道螺旋桨,研究表明悬停及小爬升状态下相比于同等尺寸的涵道螺旋桨,其拉力及功率载荷更大。
随着基于Navier-Stokes(N-S)方程的数值模拟方法的不断发展,多重参考系法(Multiple Reference Frame,MRF)、基于滑移网格及嵌套网格的非定常数值模拟方法等更高精度的CFD(Computational Fluid Dynamics)求解方法被广泛应用于涵道螺旋桨性能计算中。但由于CFD计算耗时久,尤其是非定常计算。若应用CFD计算进行性能求解,进行涵道螺旋桨的优化设计,虽然设计精度高,但设计效率低。而对于快速设计方法,由于设计方法本身存在一定简化,且需确定叶素的气动力信息,故设计性能同真实性能存在一定偏差。
因此,为提高设计的精度并保留设计的快速性,本文提出一种耦合CFD修正的涵道螺旋桨桨叶设计方法,首先采用快速设计方法进行设计,再通过CFD计算对设计进行修正,两者迭代,从而在进行少量CFD计算后,得到满足设计要求的结果。
1 涵道螺旋桨快速设计方法
1.1 最小能量损失
涵道螺旋桨叶素受力分析如图1所示。其中:为来流速度;为转速;为叶素实际迎角;为干涉角;为几何入流角;为实际入流角;为阻升角;为合速度;为轴向诱导速度;为切向诱导速度;′为几何诱导速度;为升力;为阻力;为切向力;为拉力。
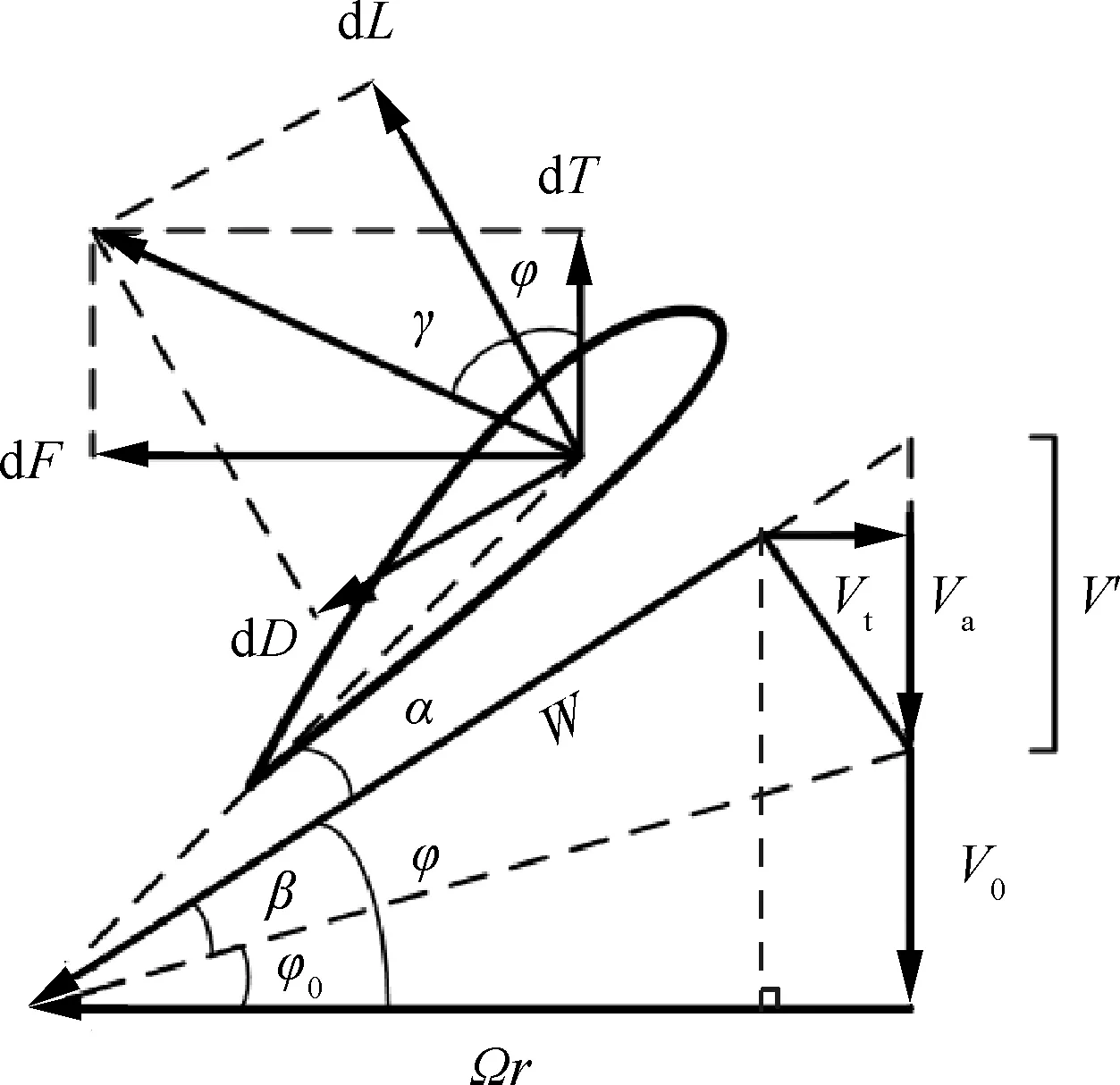
图1 叶素受力分析Fig.1 Force analysis of blade element
涵道螺旋桨桨叶设计基于最小能量损失原则。若径向位置处桨叶叶素产生增量扰动Δ,使螺旋桨拉力和扭矩分别发生Δ和Δ增量变化,则螺旋桨有用功与吸收能量对应变化的比值为
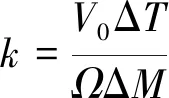
(1)
忽略阻力影响时,拉力、扭矩变化为
Δ=Δ(-)d
(2)
Δ=Δ(+)d
(3)
式中:为空气密度。
根据图1几何关系式可得
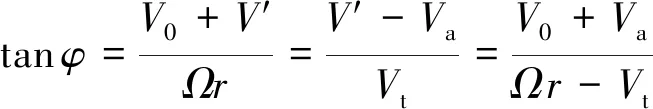
(4)
联立式(1)~式(4),可得
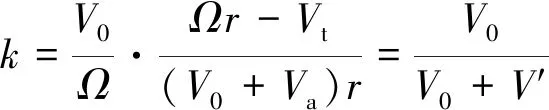
(5)
要使螺旋桨效率最高,则需在值大处增加环量,值小处减小环量。故最小能量损失要求沿桨叶分布为常数。又由式(5)可知,此时′沿桨叶的分布亦为定值。因此涵道螺旋桨桨叶的设计便是求解满足设计要求的′,进而确定各叶素的状态。
1.2 涵道螺旋桨叶素动量理论
对于涵道螺旋桨,桨叶提供一部分拉力外,涵道壁面也提供一部分拉力。假设桨叶拉力占比为,表示螺旋桨桨叶拉力,则
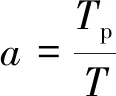
(6)
设涵道螺旋桨喷流的轴向诱导速度为,桨叶处的诱导速度为、,由动量定理及动量矩定理可知
d=2π(+)d
(7)
d=4π(+)d
(8)
d=2π(+)d
(9)
而根据动量理论可知桨叶的拉力:
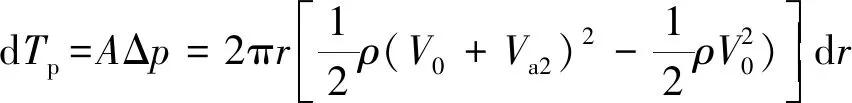
=2π(+2)d
(10)
式中:为桨盘面积;Δ为桨盘前后压差。由式(9)、式(10)求得轴向诱导速度间的关系:
=2[+(-1)]
(11)
对于涵道螺旋桨,根据图1所示叶素几何关系并结合式(8)、式(9)可知:
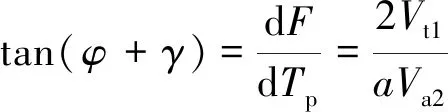
(12)
故桨叶处轴向诱导速度和切向诱导速度的关系为
=[+(-1)]tan(+)
(13)
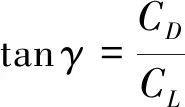
(14)
式中:和分别为升力系数和阻力系数。
又由式(4)可知:
′=tan+
(15)
联立式(13)及式(15),推导可得桨叶诱导速度同′的关系:
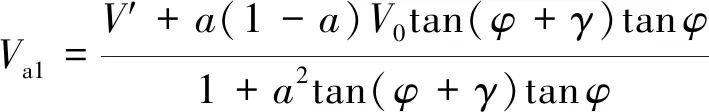
(16)
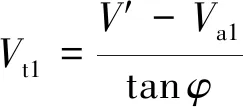
(17)
1.3 快速设计方法
给定设计高度、来流速度及设计拉力,并确定涵道外形,在此基础上进行涵道螺旋桨桨叶设计。
桨叶拉力占比与涵道外形相关,涵道外形确定则设计状态下的确定,同时螺旋桨半径确定。再选定桨叶翼型,确定设计状态下的叶素迎角、升力系数及阻力系数,通过设计得到各叶素的弦长及扭转角,从而得到涵道螺旋桨的桨叶外形。设计过程为
1) 确定桨叶数及转速,并将桨叶划分为个截面。
2) 根据设计拉力及设计状态求解′,确定处叶素的弦长及扭转角。
给定初始′,得到入流角:
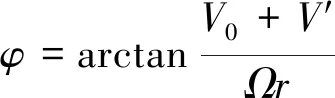
(18)
根据式(16)、式(17),可确定诱导速度,进而得到合速度及环量:
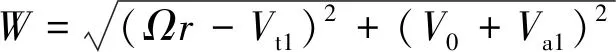
(19)
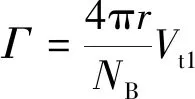
(20)
叶素升力与当地环量关系为
d=d
(21)
而升力又可表示为
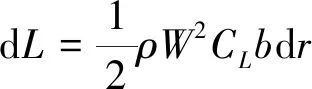
(22)
联立式(21)~式(22)可得
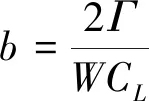
(23)
故确定合速度及环量后,通过式(23)可求得叶素弦长。
对于宽度为d的叶素,其产生的拉力d、扭矩d及总拉力d为
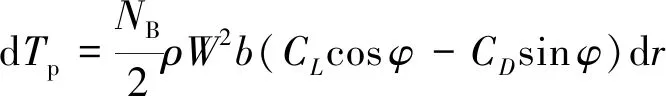
(24)
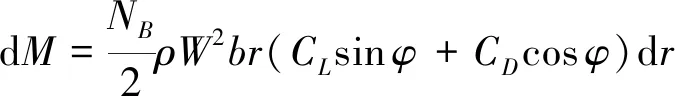
(25)
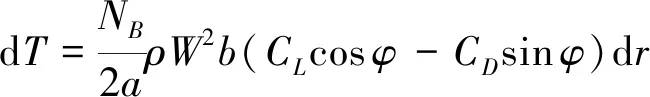
(26)
则总拉力为
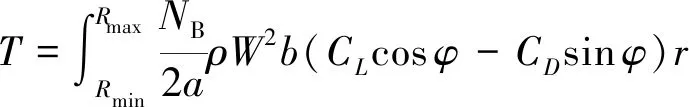
(27)
式中:和分别为桨叶的最大和最小半径。
采用Newton迭代求解上式,可得到满足设计拉力要求的′,从而确定各个截面的受力几何关系。最终得到该截面的设计弦长,及对应的扭转角:
=+
(28)
3) 重复求解,得到所有设计截面的弦长及扭转角。
2 涵道螺旋桨数值模拟方法
采用求解雷诺平均N-S方程的“多重参考系法”对涵道螺旋桨的性能进行计算,湍流模型采用SA湍流模型,并采用结构网格进行网格生成。
为验证数值模拟方法的可行性,对文献[20] 中的NASA涵道螺旋桨模型进行计算,几何模型如图2所示。该模型有3片桨叶,桨盘直径0.381 0 m,桨毂直径0.109 2 m,桨毂长0.392 7 m,涵道外壁最大直径0.464 3 m,涵道长0.261 9 m,具体尺寸详见文献[20]。
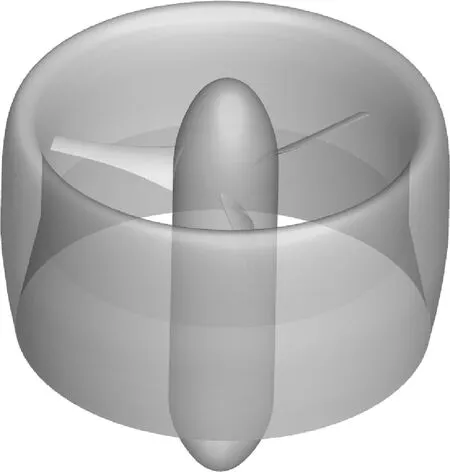
图2 NASA涵道螺旋桨几何模型Fig.2 Geometry model of NASA ducted propeller
对其进行网格划分,将计算区域分为 “旋转域”与其外的“外流域”,如图3所示,“旋转域”包含部分内壁、部分桨毂及桨叶,桨间间隙完全包含在旋转域内,两域流场交界面处采用通量的计算传递信息。生成341万及458万总网格数量的两套网格,以验证网格无关性。341万总网格数量对应的局部网格如图4所示,桨叶第1层网格对应的取1。
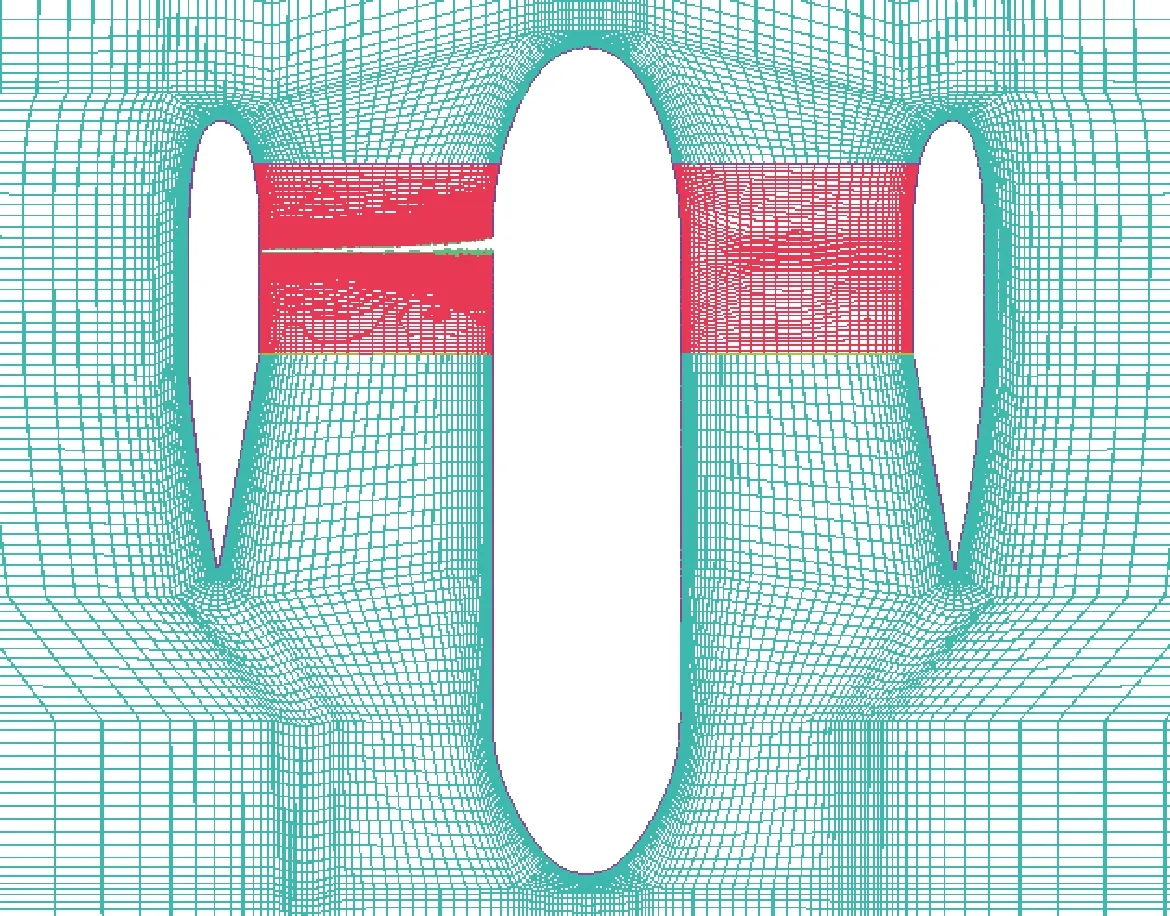
图3 不同流域网格示意图Fig.3 Grid sketch of different flow fields
采用上述方法对NASA涵道螺旋桨进行计算,计算为悬停状态,转速8 000 r/min,结果如表1 所示。
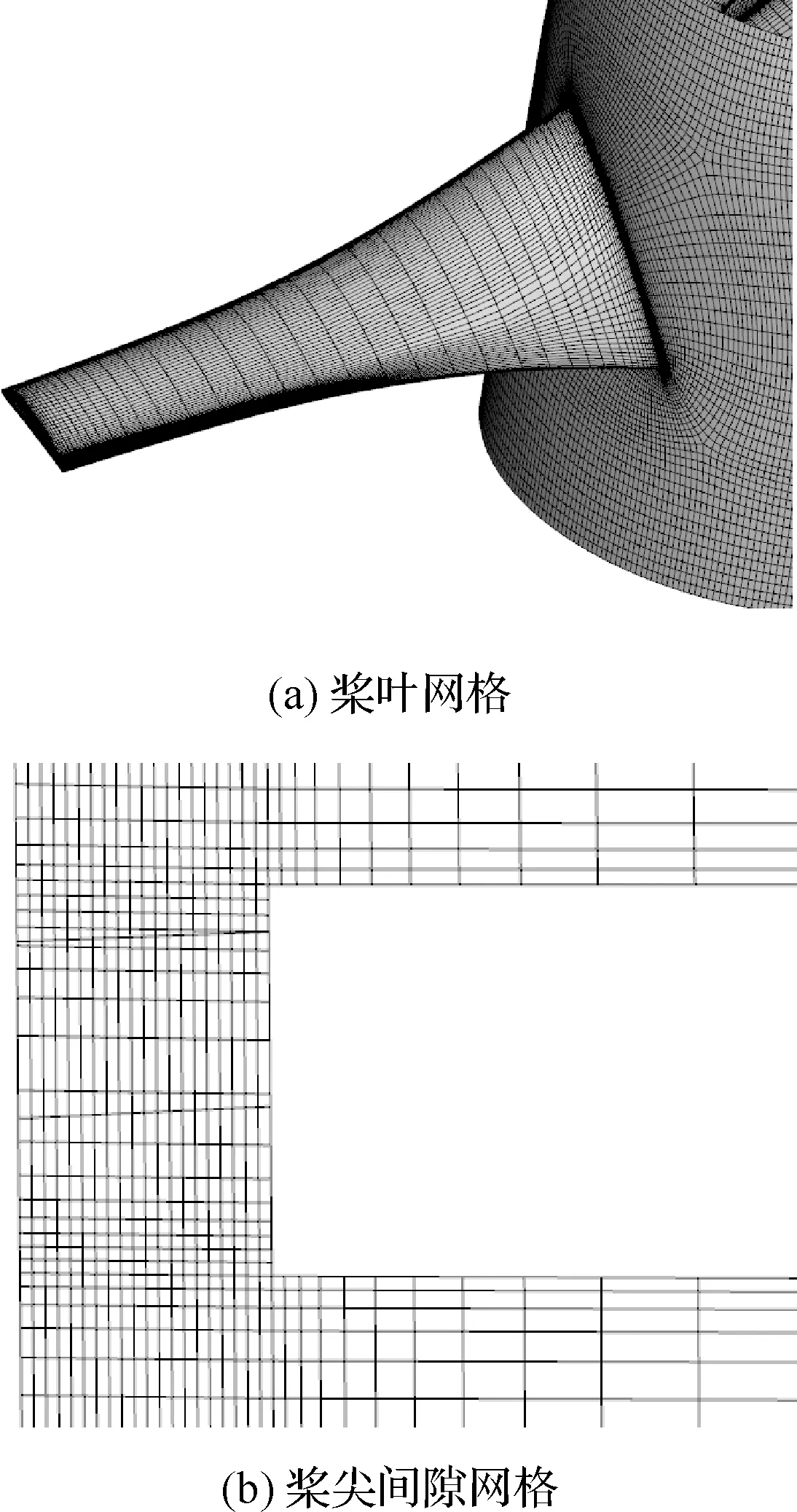
图4 局部网格示意图Fig.4 Schematic diagram of local mesh
两种网格的计算结果相差不大,“341万网格总量”的计算结果相比实验值偏小,桨叶拉力误差9.21%,扭矩误差7.05%,涵道拉力误差9.88%,所有误差均在10%以内,基本验证了所用数值模拟方法求解的可行性。下文进行相关数值模拟时保持网格拓扑结构相同,网格总量不少于341万。
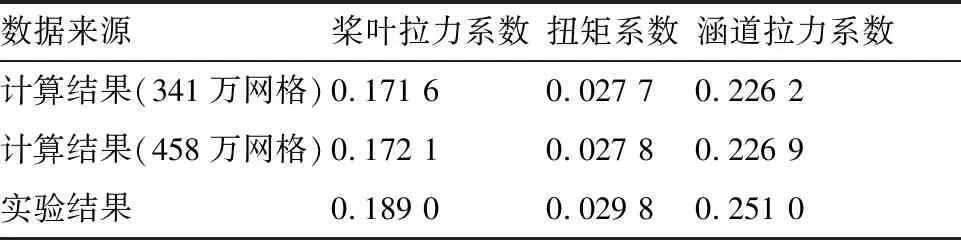
表1 气动力计算和实验结果对比
3 设计目标及结果
3.1 设计目标
采用快速设计方法进行涵道螺旋桨桨叶设计。设计高度=0 km,来流速度=0 m/s,总拉力=300 N。涵道外形采用上述“NASA涵道”,取桨叶拉力占比=0.430。桨盘半径=0.190 5 m,桨毂半径=0.054 61 m,桨尖间隙001。螺旋桨转速=8 000 r/min,桨叶数=8。
桨叶翼型采用图5所示翼型族,翼型弯度保持不变,厚度由桨根至桨尖线性减小。由于翼型的弯度一致,且厚度变化较小,故认为各翼型相同迎角下的气动力一致。给定设计迎角=2°,升力系数=0600,阻力系数=0023。
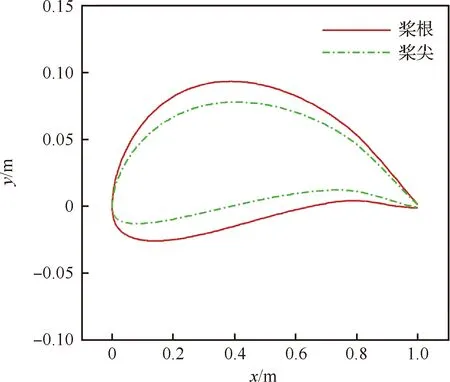
图5 翼型示意图Fig.5 Schematic diagram of airfoil
3.2 设计结果
桨叶弦长及扭转角设计结果如图6所示。采用第2节数值模拟方法进行涵道螺旋桨性能计算。
设计结果与计算结果如表2所示。可以看出,基于MRF的CFD计算得到的拉力、扭矩及功率载荷均小于设计结果,这说明上述快速设计方法存在一定缺陷。可能的原因有两方面:一方面,设计时给定的叶素气动力不能保证与实际相同,两者存在一定误差;另一方面,叶素的诱导速度不准确,设计时采用的入流角偏小,使得桨叶的扭转角偏小。
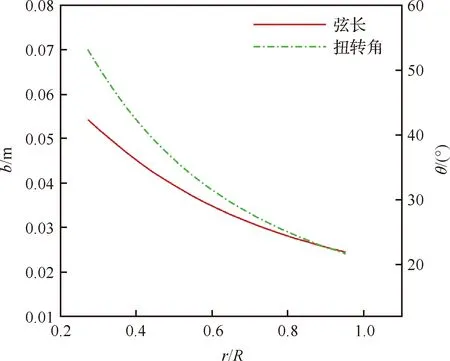
图6 弦长与扭转角设计结果Fig.6 Design results of chord length and twist angle
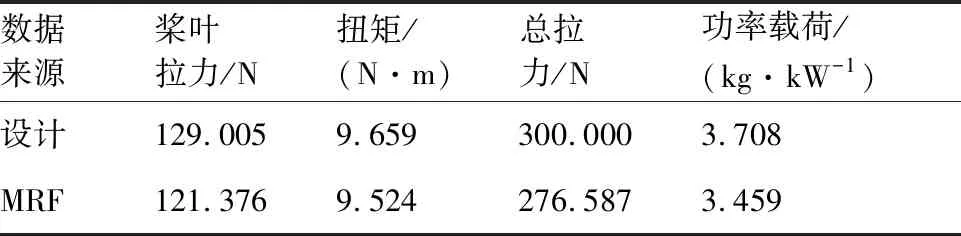
表2 涵道螺旋桨性能对比Table 2 Comparison of performance of ducted propeller
4 耦合CFD求解的高效设计方法
4.1 入流角修正
基于3.2节的分析,对文中的快速设计方法进行完善。
对于给定的′,首先按1.3节中式(18)~式(23) 计算得到弦长。但在计算桨叶气动力前,通过修正系数,对′进行修正:
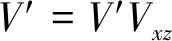
(29)
再使用新的′根据式(16)~式(19)计算修正后的诱导速度、入流角及合速度,最后计算修正后的叶素气动力。
对′进行修正是为了保证最小能量损失原则在修正后同样满足,以避免修正导致效率降低。
采用修正的快速设计方法对涵道螺旋桨桨叶进行设计,不同修正系数对应的CFD计算结果如表3所示。可以看出,当=105时,CFD计算结果与设计值接近,说明通过合理的修正,能够提高设计的精度。
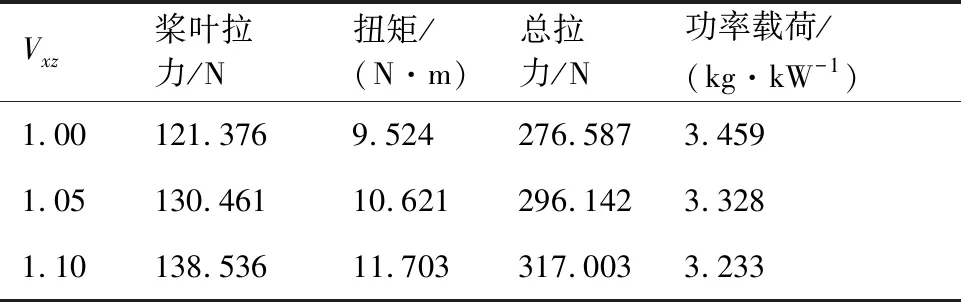
表3 不同修正系数下的涵道螺旋桨性能对比
4.2 气动力修正
叶素真实状态下的迎角及升阻力系数与设计给定的值存在一定偏差,若忽略阻力的影响,可认为气动力的偏差为迎角与升力系数的不匹配。因此,这里不改变升阻力系数,通过修正迎角进行气动力的修正。
4.3 拉力占比修正
实际设计时,涵道外形根据设计而定,也是一个未知的变量,设计前往往不能确定设计状态下拉力占比的准确值。因此,设计前可首先给出的初值,在设计迭代中,根据CFD计算结果更新,从而使设计结果更准确,也使设计方法适用于不同涵道外形的涵道螺旋桨。
4.4 修正参数求解
引入′修正对设计方法进行改善,取得了较好的效果,但其前提是得到合理的。而不同设计状态下可能不同,若通过试错来选取,可能需大量的CFD计算验证,使得设计效率降低。实际上,CFD计算结果可作为一种重要的参考,为的选取提供参考。因此这里提出一种通过CFD计算结果反解修正参数的方法。
该方法的思想是:通过构造满足CFD结果的叶素状态,求解真实状态下的入流角,确定修正系数;并对给定的叶素气动力进行修正,修正设计给定的迎角;最后更新桨叶的拉力占比。具体步骤如下:
给定初始,以CFD求解得到桨叶的拉力为设计目标,采用修正的快速设计方法进行桨叶设计,得到设计的拉力及扭矩。
由于叶素阻力较小,且入流角一般较大,因此忽略阻力影响时,由式(24)、式(25)可知:
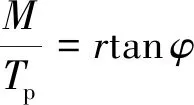
(30)
桨叶拉力及扭矩实际反映了真实的入流角。故通过迭代求解,最终得到与CFD所得相同的设计结果,此时的即为入流角修正系数。
获得的同时得到修正后的入流角,已知涵道螺旋桨的扭转角,进而根据式(28) 求得各叶素的迎角,求其均值得到修正迎角:
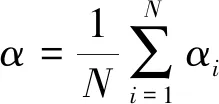
(31)
最后根据CFD计算得到的总拉力及桨叶拉力,由式(6)求得真实的拉力占比。
4.5 耦合CFD求解的涵道螺旋桨桨叶设计
基于以上方法及分析,提出耦合CFD修正的涵道螺旋桨桨叶高效设计方法,步骤如下:
根据1.3节快速设计方法,设计得到初始桨叶(弦长及扭转角分布)。
通过CFD计算获得桨叶拉力及扭矩。
根据CFD计算结果求解修正系数及修正迎角,并更新桨叶拉力占比。
根据求得的修正参数采用修正的快速设计方法进行再设计。
重复步骤2~步骤4,得到满足设计要求的结果。
设计流程如图7所示。
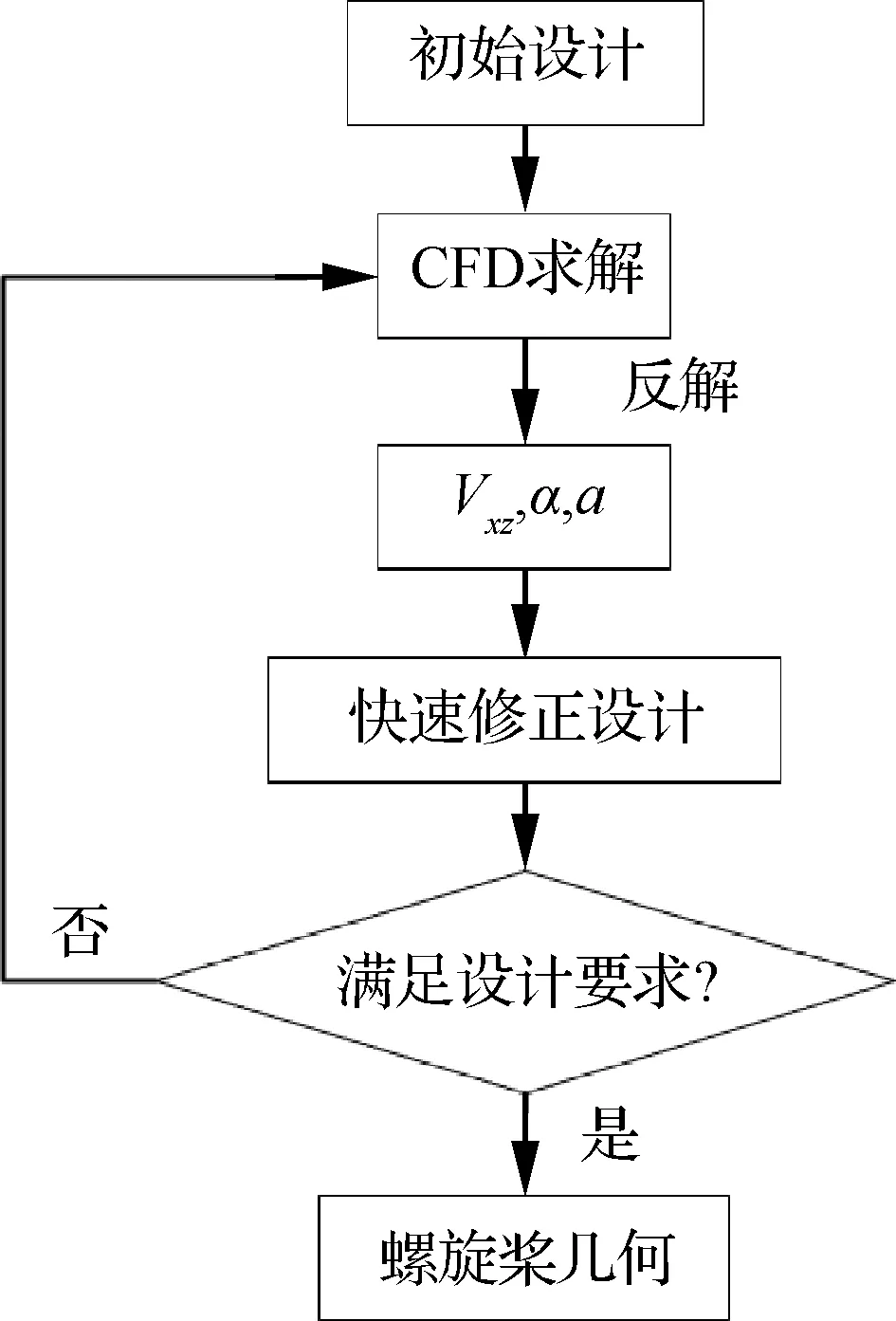
图7 耦合CFD求解的涵道螺旋桨桨叶设计流程Fig.7 Design process of ducted propeller blade coupled with CFD correction
5 结果与分析
5.1 修正结果对比
采用修正设计方法对表2的初始结果进行修正,以此再设计,结果如表4所示。修正2次后的CFD结果已经十分接近设计结果,对应=1094,=1215°,=0438。设计得到的涵道螺旋桨几何如图8所示。
为证明方法的可行性,对表3中=110的初始设计进行修正及再设计,结果如表5所示。同样,修正2次后,CFD结果基本与设计结果相同,满足设计要求。一方面,说明文中的设计方法具备快速收敛的特点;另一方面,设计结果与CFD计算结果间的差距随着设计迭代次数的增加而逐渐减小,最终趋于一致。

表4 修正前后涵道螺旋桨性能
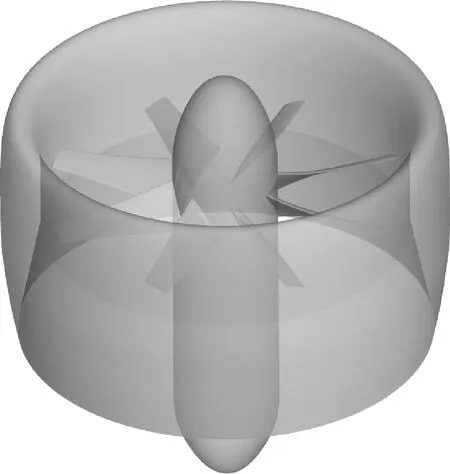
图8 涵道螺旋桨几何Fig.8 Geometry of ducted propeller
经2次修正设计后,各修正系数分别为:=1095,=1187°,=0435,与上述修正参数结果基本相同。进一步对比弦长及扭转角设计结果,如图9所示,两者几何也基本一致,说明不同初始位置最终收敛至同一结果。表明文中采用的设计方法是收敛的,同时具备较好的鲁棒性。
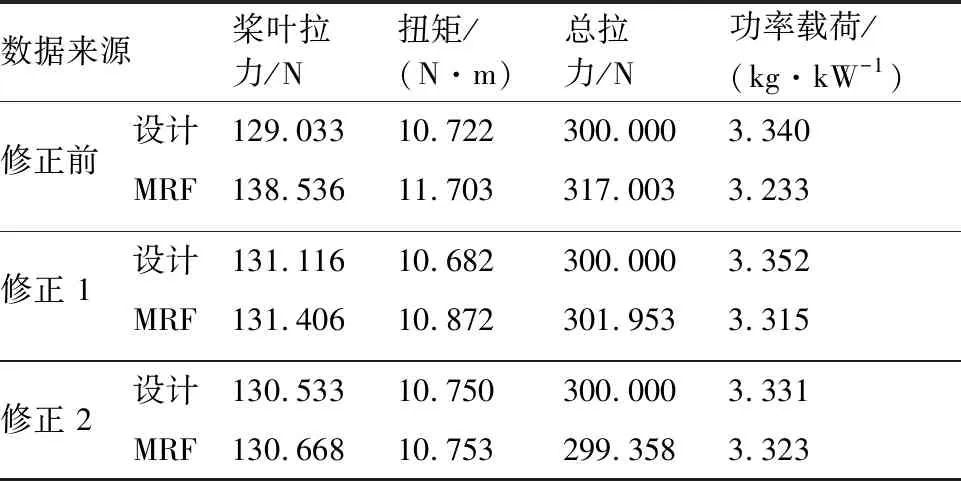
表5 修正前后涵道螺旋桨性能(Vxz=1.1)
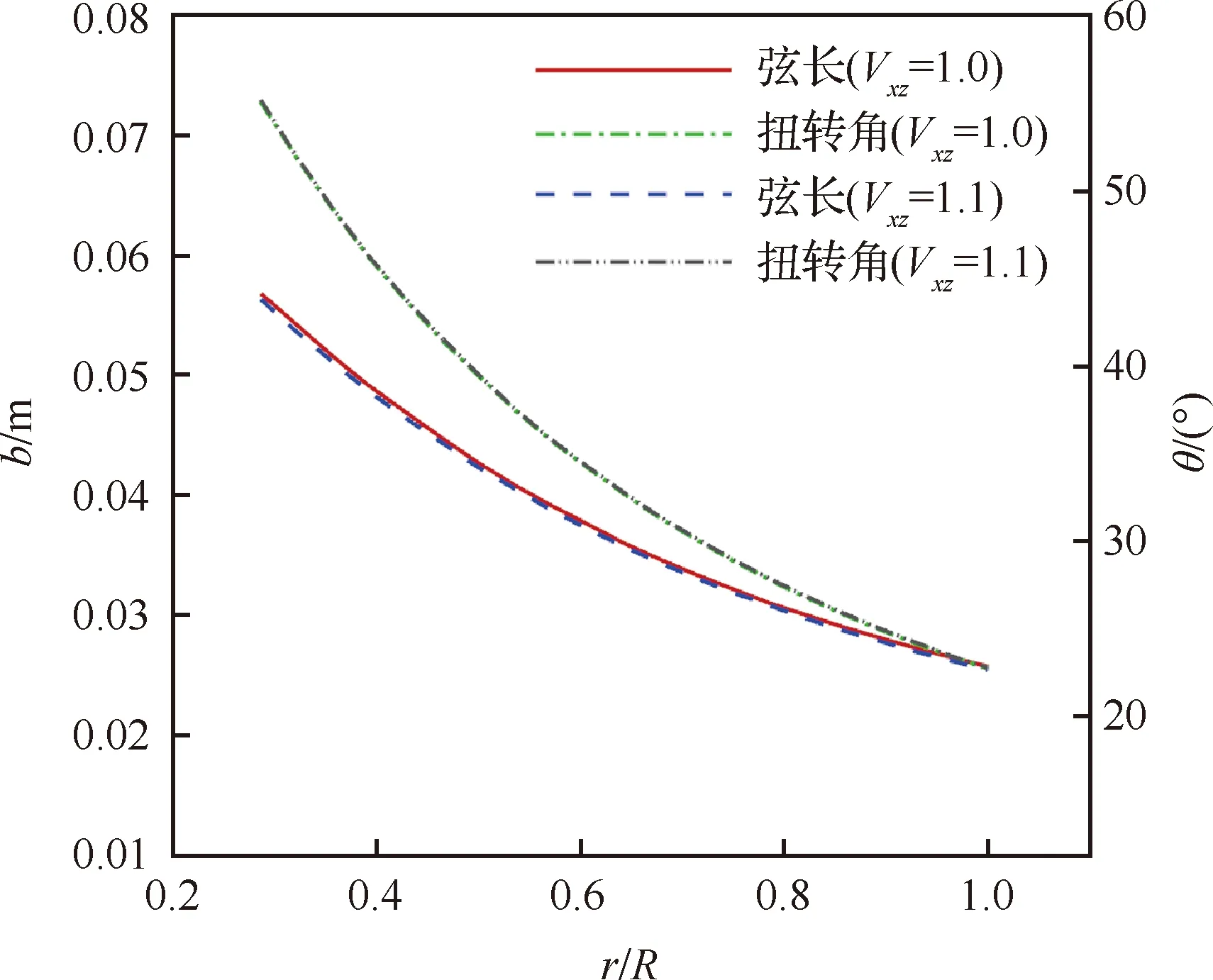
图9 不同初始修正系数设计得到的弦长与扭转角设计对比Fig.9 Comparison of chord length and twist angle obtained by design of different initial correction factors
5.2 不同涵道外形设计验证
为进一步验证设计方法,设计一种小型涵道螺旋桨。并采用图10所示的无扩张及收缩出口的简易涵道外形,以检验设计方法在不同涵道外形下的可行性。

图10 简易涵道外形示意图Fig.10 Schematic diagram of a simple shape of duct
取设计高度=0 km,来流速度=0 m/s,总拉力=15 N,桨盘半径=0.050 m,桨毂半径=0.020 m,桨尖间隙001。取螺旋桨转速=20 000 r/min,桨叶数N=8,初始桨叶拉力占比初值=0500。同样采用图2所示翼型族,给定叶素设计迎角=2°,升力系数=0600,阻力系数=0023。
初始设计取=1000,小型涵道螺旋桨的设计结果如图11及图12所示,修正前后的性能见表6。可以看出,设计结果与计算结果趋于收敛,经过2次修正设计,基本满足设计要求,对应=1060,=0574°,=0581。
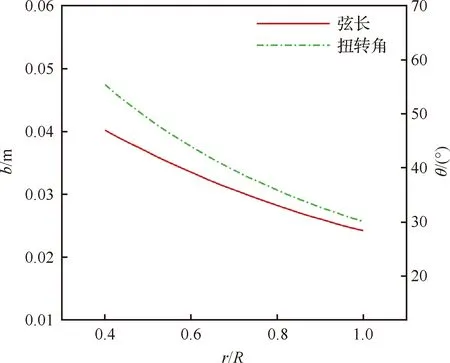
图11 小型涵道螺旋桨弦长与扭转角设计结果Fig.11 Design results of chord length and twist angle of small ducted propeller

图12 小型涵道螺旋桨几何Fig.12 Geometry of small ducted propeller
涵道外形对设计的影响体现在桨叶拉力占比之上。对于该简易涵道,可认为喷流无扩张和收缩,而桨毂的存在使得喷流存在一定的收缩,因此设计结果>0500,符合动量理论的结论。同时也验证了本文所采用的设计方法适用于不同涵道形式。
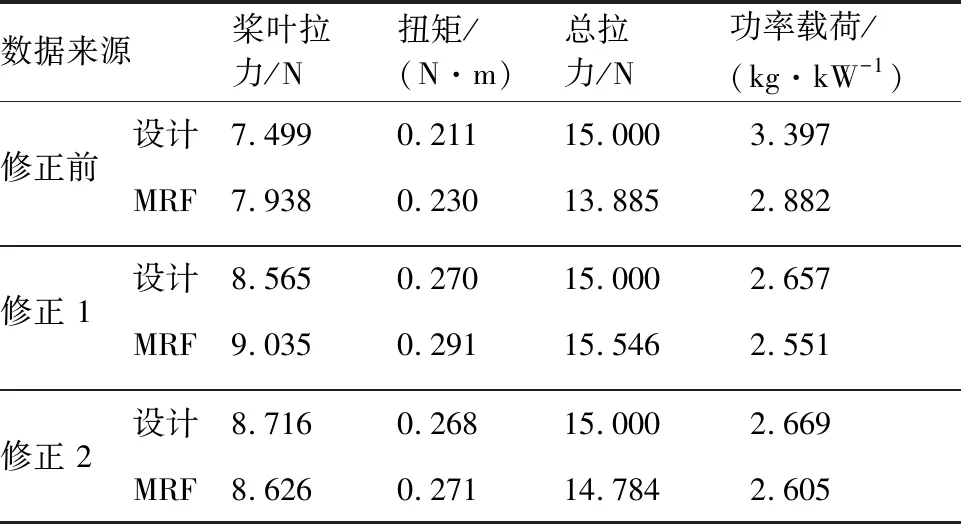
表6 修正前后小型涵道螺旋桨性能
5.3 有来流状态设计验证
以上设计均在无来流状态下进行设计,为验证设计方法在有来流状态下的可行性,在3.1节设计状态的基础上,改变来流速度为=20 m/s,同时改变桨叶拉力占比初值=06,以此进行设计。
有来流状态涵道螺旋桨的设计结果如图13及图14所示,设计前后的性能见表7, 最终修正参数=1078,=1056°,=0577。可以看出,经过2次修正设计后,设计与计算间的拉力误差基本控制在2%以内,验证了文中涵道螺旋桨桨叶设计方法在有来流状态下设计的可行性。
以上设计验证均表明,文中的设计结果收敛于CFD计算结果。因此,只需保证CFD计算的准确性,则能保证文中设计方法设计的准确性。
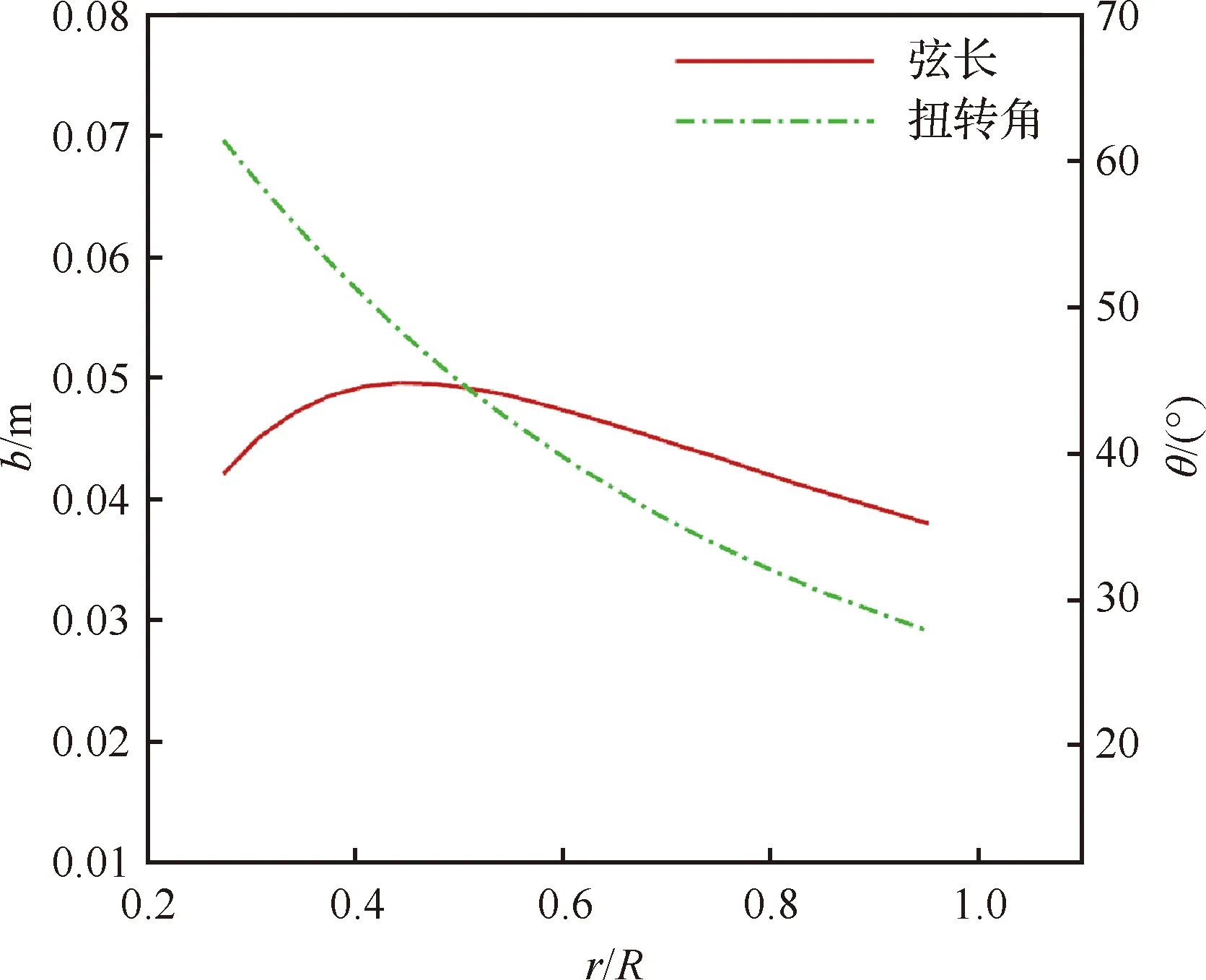
图13 有来流状态涵道螺旋桨弦长与扭转角设计结果Fig.13 Design result of chord length and twist angle of ducted propeller in incoming flow state
图14 有来流状态涵道螺旋桨几何Fig.14 Geometry of ducted propeller in incoming flow state
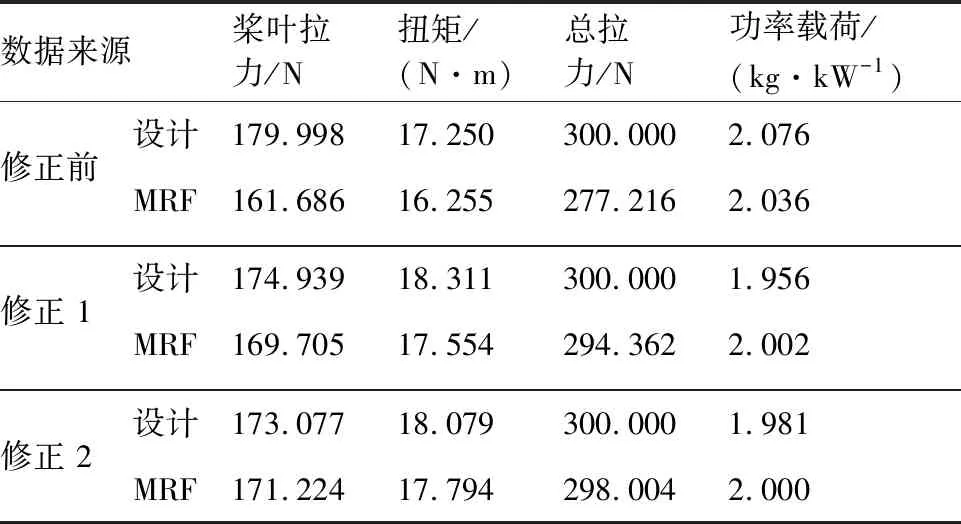
表7 有来流状态修正前后涵道螺旋桨性能
6 结 论
本文建立了基于叶素动量理论的涵道螺旋桨快速设计方法,并通过耦合CFD计算对叶素入流角及迎角进行修正,提出了一种涵道螺旋桨桨叶高效设计方法,并通过对不同状态的涵道螺旋桨进行设计及计算,验证了方法的可行性。得到的结论如下:
1) 基于叶素动量理论的快速设计方法,设计前不能准确地给出叶素气动力及桨叶拉力占比,导致设计的入流角与实际结果存在一定差距,因此造成设计结果与CFD计算结果间的偏差。
2) 涵道外形对设计的影响体现在桨叶拉力占比之上,而桨叶拉力、扭矩的比例反映了叶素入流角信息。通过对CFD计算结果进行反解,可得到真实的叶素入流角,进而求得真实的叶素迎角,同时求得真实的桨叶拉力占比。
3) 通过求解入流角修正系数、修正迎角及真实桨叶拉力占比,并以此进行涵道螺旋桨桨叶的再设计,可得到趋于设计要求的结果。不同初始结果、不同涵道外形及不同设计状态的设计验证表明,文中设计方法基本进行2次CFD计算修正与再设计便能满足设计要求,设计高效。
4) 本文设计方法的设计结果与CFD计算结果间的差距随着设计迭代次数的增加而逐渐减小,设计结果最终收敛于CFD计算结果。因此,确保CFD计算的准确性,则能够确保设计方法的准确性。
