基于部分输出FFT的CSK信号高效解调算法

李晔，周国栋，肖林伟，陈华明

( 1. 湖南开放大学 网络技术学院, 长沙 400004；2. 国防科技大学 电子科学学院, 长沙 410073 )

0 引 言

全球卫星导航系统(GNSS)作为信息化时代重要的基础设施，在军事、民用、科学等领域发挥着重要的作用[1]. 随着卫星导航系统应用的不断深入，目前GNSS已无法满足智能驾驶等场景中用户对厘米级定位精度的需求，而基于低轨导航增强系统的精密单点定位(PPP)技术被广泛认为是最具潜力的解决方案[2].

PPP技术要求用户能够通过导航电文中的精密星历实时解算得到卫星的精密轨道和精密钟差. 为了实现精密星历数据的实时播发，电文速率要达到Kbps量级，这远高于目前GNSS所采用的100 bit/s左右的电文速率[3]. 为了能够在不影响测距性能的前提下提高电文速率，同时兼具测距精度和电文速率的码移键控(CSK)调制成为低轨导航增强系统信号调制技术的重要选项[4].

CSK 调制在上世纪九十年代就已被提出，该调制在相位或幅度等调制技术的基础上额外增加码相位偏移维度，从而能够在不改变原有信号频谱的基础上提高电文速率[5-8]. 但码相位偏移的改变同时也显著增加了接收端电文解调的复杂度，这一缺点致使该技术在数字处理能力较弱的年代始终未得到广泛应用. 随着集成电路技术的快速发展，CSK信号解调的高复杂度已不再是制约其应用的主要瓶颈，而其优良的测距和通信性能重新得到了卫星导航系统设计者的广泛关注[9-13]. 目前CSK 调制在日本的准天顶系统(QZSS)中已经得到应用，实现了速率为2 000 bit/s的电文传输[14]. 据了解，国内某些低轨导航增强系统也在积极开展CSK调制信号的验证工作. 文献[15]探讨了卫星导航系统同时采用CSK调制与低密度奇偶校验码(LDPC)等编码技术相的误码率性能. 可以预见，CSK调制将以低轨导航增强为代表的下一代卫星导航系统中得到广泛的应用. 除了卫星导航系统以外，在超宽带(UWB)通信系统中也使用CSK调制技术以提高电文速率[16].

导航接收机在接收CSK调制信号时，除了要完成信号跟踪以外，还需要遍历计算各种码相位偏移的相关值，从而解调出码相位偏移所携带的电文信息，这相比传统导航信号采用的二进制相移键控(BPSK)和BOC调制具有更高的实现复杂度. 针对CSK信号解调算法复杂度较高的问题，本文提出了基于奇偶分块快速傅里叶变换(FFT)的高效解调算法，该算法能够显著提高相关值计算效率，为低轨导航增强系统接收机的设计提供重要参考.

1 CSK调制的信号模型

CSK调制的基本原理是通过增加伪码相位偏移这一维度，在不改变信号带宽、幅度等参数的情况下提高信息传输速率. CSK调制是一种M进制正交信号，每个符号都是通过对一个原始的伪码序列进行循环移位得到. 如果每个扩频码周期需要发送U个比特，那么需要M=2U个不同的伪码相位偏移来表示.假设CSK调制相位偏移为0的原始伪码序列为c0(t) ，那么剩下的M-1 个 伪码序列cm(t) (1 ≤m≤M)可表示为

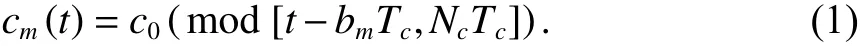
式中：bm为第m个 伪码序列的伪码相位偏移数；Nc为扩频码周期数；Tc为每个扩频码码片时长；mod(x,y)为x对y取模. 上述表示比特数为U、扩频码周期为N的CSK调制，通常简记为 C SK(U,N) .

理论上而言，伪码序列cm(t)对应的U比特电文序列表示第m种比特序列中的第i比特，取值为0或1)与其对应伪码相位偏移数bm只需满足一一映射的要求即可. 实际使用中，为了简化接收端的解调，伪码相位偏移数bm通常正好对应着比特电文序列dm的十进制数 (dm)10，即

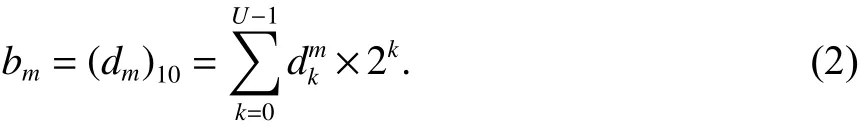
根据上述CSK调制符号的表达式，可以得到用户接收到的CSK调制信号的模型为

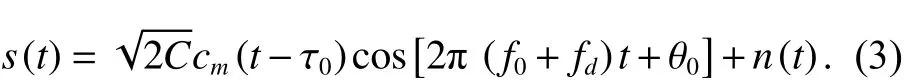
式中：C为信号功率； τ0为信号传输时延；f0为标称的射频频率；fd为多普勒频率； θ0为载波初相；n(t) 为噪声.

2 CSK信号的时域解调算法

CSK调制信号的扩频码周期存在M种可能的码相位偏移，因此在进行电文解调时需要同时计算M种码相位偏移的相关值，并根据最大相关值所对应的码相位偏移得到当前扩频码周期调制的电文. 在不影响算法原理的前提下，为了表述的简洁，文中将不考虑接收机的二次变频过程.

假设扩频码周期为T，则第i个扩频码周期码相位偏移为m个码片时所对应的相关值xm[i] 为

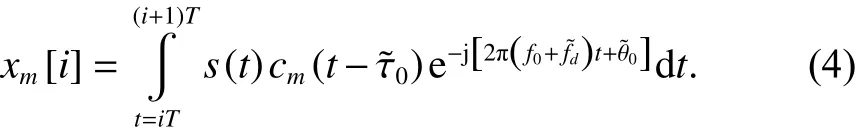
在得到各种码相位偏移相关值的基础上，进行电文解调的方法包括相干解调和非相干解调，其表达式分别为：

式中， R e(x) 为取复数x的实部.

根据上述表达式，可以得到CSK调制信号的时域解调算法，其实现框图如图1所示.

图 1 CSK调制信号的时域解调算法的实现框图

为了简洁，图1中省略了载波和伪码跟踪部分的实现框图. 由图1可知，相比BPSK信号的解调，CSK信号解调需要同时计算M个相位. 随着M值的增加，CSK信号解调所需的硬件资源会急剧增加，当M接近扩频码周期数N时，不同偏移码相位相关值计算的复杂度近似为O(N2).综上所述，CSK信号解调算法的关键在于如何高效计算不同偏移码相位的相关值.

3 CSK信号的频域解调算法

为了解决不同码相位相关值的高效计算，文献[7]提出了CSK信号频域解调算法. 该算法通过将时域的循环相关转换为频域相乘运算，从而实现CSK信号的高效解调.

假 设两个长 度 均为N的 有限长 序 列x[i] 和y[i]( 0 ≤i＜N)，其循环相关值z[i] ( 0 ≤i＜N)的表达式为

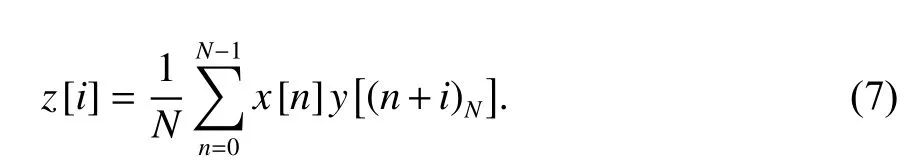
式中， (y)N=mod(y,N) 表示将y对N取模.

那么序列x[i] 、y[i] 和z[i] 的离散傅里叶变换存在如下的关系：

利用上述关系，对Z[k] 进行FFT逆变换就可以得到循环相关值z[i] . 很显然，上述基于频域的相关值计算方法的复杂度主要取决于时频域变换. 众所周知，当离散傅里叶变换的点数N刚好等于2的幂次时，可以使用计算复杂度为ONlog2N的FFT来实现，因此频域处理可以将计算复杂度由O(N2)降为

根据上述循环相关的频域高效实现，可以得到CSK信号的频域解调算法. 下面首先考虑数字处理接收机计算码相位偏移为0的计算过程，其表达式为

式中：Ts为采样周期；N=[T/Ts] 为扩频码周期内的采样点数；s′[k] 为 经过载波剥离后的基带信号；c0[k] 为码相位偏移为 0 的伪码采样序列.

很显然，通过对序列s′[k] 向右作l个采样点的循环移位，可以计算得到基带信号相对于c0[k] 码相位偏移为lTs/Tc个码片的相关值，即

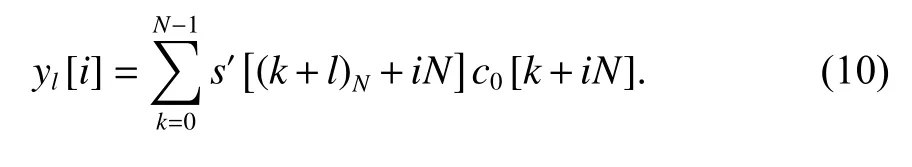
为了降低基带处理的计算复杂度，在满足Nyquist曲线采样定理的前提下，接收机通常会尽可能降低基带数据速率. 对于CSK调制信号而言，基带数据只需略高于2倍码率，即Tc≈2Ts. 如果基带数据速率与2倍码率之间相差较大，可通过数据重采样使得基带数据速率满足上述要求. 在基带数据速率近似等于2倍码率的条件下，通过计算相关值y2m[i] 即可近似得到xm[i] ，即

很显然，上式中y2m[i] 的计算过程为循环相关结构. 利用循环相关与频域乘积之间的对偶关系，可以使用FFT实现高效的计算，即

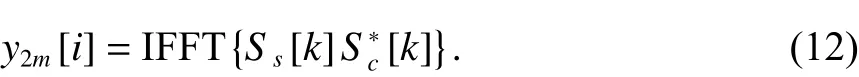
式中，Ss[k] 和[k] 分别为s′[k] 和c0[k] 的离散傅里叶变换.

根据上述表达式，可以得到CSK信号频域解调算法的实现结构如图2所示.

图 2 CSK信号频域解调算法的实现框图

4 基于部分输出FFT的解调算法

在CSK频域解调算法中，式(12)中的快速傅里叶逆变换(IFFT)运算同时给出了所有码相位偏移的相关值计算结果，然而在CSK调制中，只有前U个码相位偏移是可能的，因此可以对IFFT运算进行优化，只需要计算与前U个码相位所对应的相关值即可，从而可以简化解调过程的计算量，这就是本文所提算法的基本原理. 由于FFT和IFFT旋转因子和系数存在差别，但实现结构基本是一致的，因此本文仍以FFT为例介绍所提算法的原理.

FFT算法是蝶形递推运算，以Cooley-Turkey算法为例，当FFT点数为8时，其实现结构如图3所示.

在传统FFT运算中，输出点数和输入点数一致.当FFT点数为 2L时，FFT运算共包括L级蝶形运算，每级蝶形运算包含 2L个计算节点. 以图3中的8点FFT为例，运算结构共包含3级蝶形运算，总共包含24个计算节点.

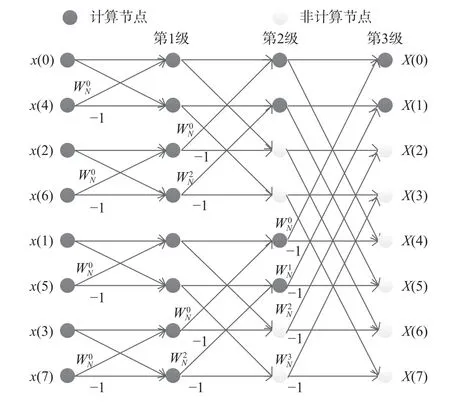
图 3 8点FFT的蝶形递推运算结构

由于CSK信号频域解调算法只需使用FFT运算的部分结果，因此并不需要对所有计算节点进行处理. 在图3所示的8点FFT中，当输出前面2个点时，计算节点数目为14个，其余10个非计算节点与最终输出结果无关，约占总节点数的41.7%. 很显然，输出点数相对输入点数的比例越低，计算节点在总节点数中占比越小. 因此基于部分输出的特点，通过优化FFT的计算结构，可以降低CSK信号频域解调算法的计算量.

考虑一般情况，假设FFT输入点数为 2L，需要输出的为序号0～2M-1的结果. 根据图3中计算节点的规律进行递推，可以得到基于部分输出FFT计算结构具有如下特点[17]：

1) 前面M级的蝶形运算与传统FFT完全一致，所有节点均为计算节点；

2) 从M+1 列开始，仅对两个输入节点均为计算节点的蝶形运算进行处理，且只有前一个输出为计算节点.

在上述条件下，可以得到基于部分输出FFT的CSK信号频域解调算法的实现框图，具体如图4所示.

图 4 基于部分输出FFT的CSK信号频域解调算法的实现框图

根据部分输出FFT计算节点的分布，可以得到部分输出FFT的计算节点数为

由于传统FFT的计算节点数为L×2L，因此部分输出FFT相比的传统FFT计算节点的占比为

当L和M取不同值时，部分输出FFT相比的传统FFT计算节点的占比如图5所示.

5 仿真验证

下面以码率为1.023 Mcps的 C SK(4,1023) 调制信号为例进行仿真验证.

假设基带数据采样率为4 Msps，通过重采样后将基带数据速率变为2.046 Msps，那么在1 ms的扩频码周期内的采样点数为2 046，因此基于部分输出FFT的频域解调算法的输入点数2 048，输出点数为32. 易知，此时部分输出FFT的计算节点数仅为传统FFT的54.4%，可节省约45.6%的计算量.

当输入信号的载噪比为40 dB·Hz，正确的码相位偏移为10时，基于部分输出FFT得到的不同码相位下的相关值如图6所示.

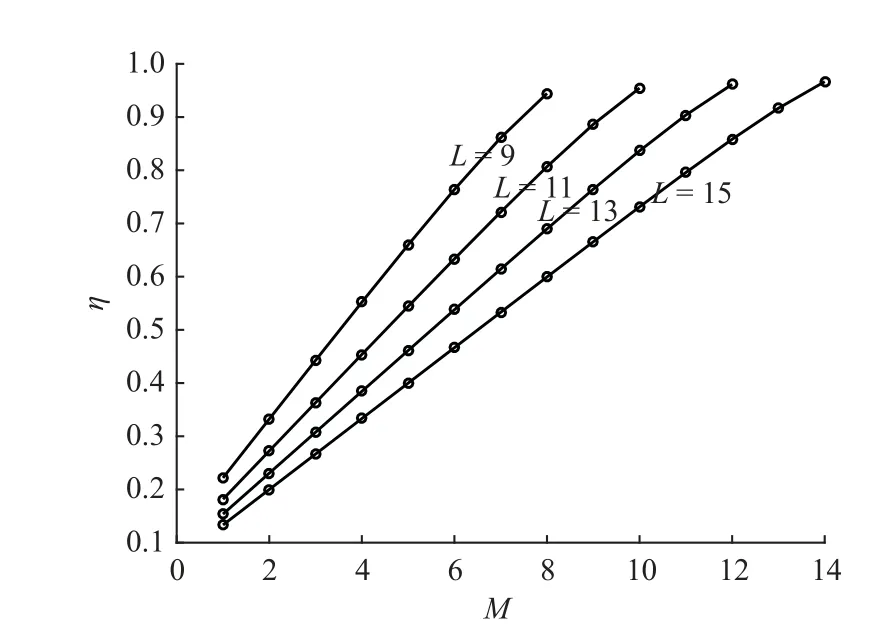
图 5 不同L和M取值时部分输出FFT相比的传统FFT计算节点的占比

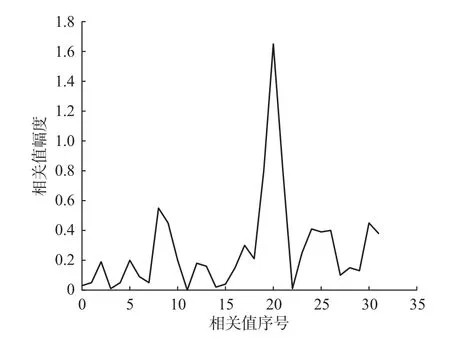
图 6 基于部分输出FFT频域解调算法得到的相关值

由图6可知，序号为20(码相位偏移为10)所对应的相关值幅度最大，与仿真设置的条件是一致的，因此本文所提出的基于部分输出FFT的频域解调能够估计出正确的码相位偏移，从而完成电文的解调.

6 结束语

针对CSK信号频域解调算法复杂度较高的问题，提出了基于部分输出FFT的高效解调算法. 该算法利用CSK解调仅需FFT部分输出结果的特点，对FFT的蝶形解算结构进行优化，通过定义计算节点来避免与输出结果无关的无效计算，从而提高整体的计算效率. 以码率为1.023 Mcps的CSK(4,1023)调制信号为例，本文所提出的基于部分输出FFT的频域解调算法可节省约45.6%的计算量，这对下一代卫星导航接收机的设计具有重要的意义.