基于独立分量法的新疆GNSS时间序列共模误差分析

雷传金，魏冠军，高茂宁，张沛

( 1. 兰州交通大学 测绘与地理信息学院, 兰州 730070；2. 地理国情监测技术应用国家地方联合工程研究中心, 兰州 730070；3. 甘肃省地理国情监测工程实验室, 兰州 730070 )

0 引 言

全球卫星导航系统(GNSS)能提供高精度、可靠的坐标时间序列，现已广泛应用于地球物理研究中，如板块运动变化、参考框架构建与维持、区域地壳形变等[1-3]. 然而，GNSS观测数据中存在一种与空间相关的噪声，即共模误差(CME)[4]. CME的存在会影响测站的参数估计，增加了测站参数信息的不确定性，这将导致解译出不准确的地球物理信息，故需采用滤波方法来削弱其干扰，以便解译出真实的地球物理信息. 针对这一问题，国内外学者们引入了堆栈法[4]、奇异谱分析[5]、主成分分析(PCA)[6-7]等滤波方法成功分离出CME. 在这些方法中，PCA滤波应用最为广泛，该方法是基于二阶统计量将输入信号分解成方差最大分量来提取CME[6]，但未充分利用CME的高阶统计信号，使得某一成分包含不同的地球物理信息，在一定程度上影响了CME分离的准确性[8].

相较于PCA，独立分量分析(ICA)是一种基于高阶统计量对盲源分离的信号进行分解的方法，对分离出独立的非高斯信号方面展现出优越的性能，能有效地分离出独立的信号[9]，现已广泛用于大地测量数据处理，如GNSS时间序列分析[8-9]、全球时变重力信号提取[10]、InSAR时序分析[11]等领域. 在GNSS网空间滤波应用中，文献[8]使用ICA方法对中国区域的259个GPS站进行滤波分析，取得较好地滤波效果，但ICA分离后信号显著性问题未得到较好地解释，未讨论滤波后对测站速度场、周期项的影响.

新疆地区是盆地、山地地震构造区，是研究地壳运动的良好试验场，但一些学者在提取区域地球物理信号时，仅考虑时域上的噪声项影响，未考虑空域上的CME. 因此，本文引入ICA对新疆地区GNSS坐标时间序列CME进行提取，并与PCA滤波效果进行对比分析，验证了ICA在提取区域CME时的可行性，为CME物理成分的科学解释提供参考. 此外，高精度地提取线性速率等地球物理信号，为更好地解释这一区域的构造运动提供参考价值.

1 空间滤波

1.1 PCA空间滤波

设某一区域有m个时间跨度为n天的观测站，且n＞m，数据矩阵X(n×m) 为测站的残差序列，则可计算X的协方差阵CX

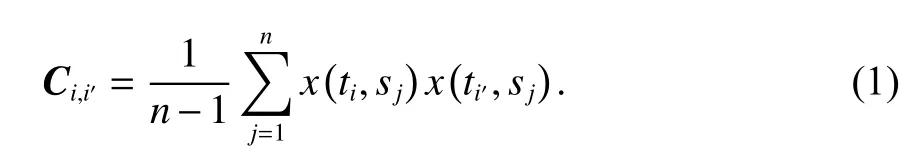
对CX进行正交分解

式中：Λ为具有r个非零特征值的对角矩阵；V为m×m维特征向量矩阵. 采用正交基V来扩充X矩阵，可得

即

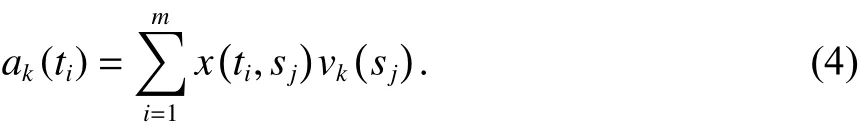
式中：ak(t) 为X的第j个主分量；vk(s) 为对应主分量ak(t) 的空间响应(SR). 将得到的特征值 λi降序排列，以便提取X中的CME信号. 假设前p个方差较大的主分量代表CME，则CME可表示为[6]

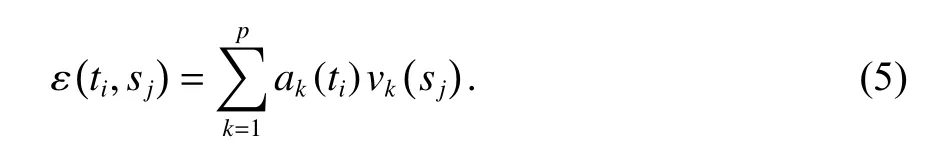
1.2 ICA空间滤波

设有m个时间序列为X的观测站，每个观测序列Xi(t)=[x1(t),x2(t),···,xn(t)]T可由n个相互独立的未知信号y进行叠加，某一历元t的线性表达式为

式中：xt为t时刻m×1 维 观测向量；为t时刻第j个信号源；aij为第j个信 号 源对i个观 测值的空间响 应 情况，且满足1 ≤i≤m,1≤j≤n. 将所有观测数据写成矩阵形式

引入混合矩阵W来恢复A的 原始信号，即W=A-1. 为了解算W，本文利用基于负熵峭度的鲁棒方法计算非高斯性. 其近似负熵为

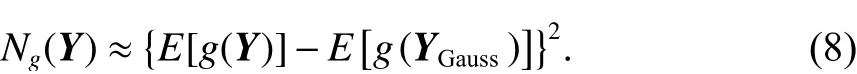
式中：Y=WTZ代表独立分量，Z为观测向量中心化、白化处理后的值；g函数的形式为g(y)=yexp(-y2/2)，通过式(8)便可得到W的最优解及每个独立分量. 本文采用文献[9]中时域上相互独立的tICA进行解算混合矩阵W，并计算出第k个独立信号的贡献率为

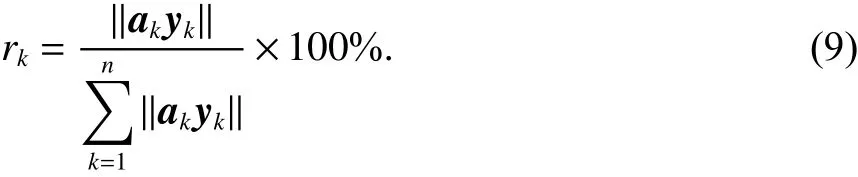
式中： ‖ ·‖ 为F-范数；rk为第k成分的贡献率. 将所有独立分量按贡献比降序排列，用前几个显著的独立分量表示最显著信号，则CME可表示为[8]

2 GNSS数据处理

本文对我国新疆地区连续站的原始GNSS时间序列进行CME分析，分析站点的时间跨度为2011—2018年，数据缺失率较低，平均缺失率为5%，能够有效地避免数据缺失对主频项分析的影响. 数据来源于中国地震局GNSS数据产品服务平台，GNSS站点分布如图1所示.

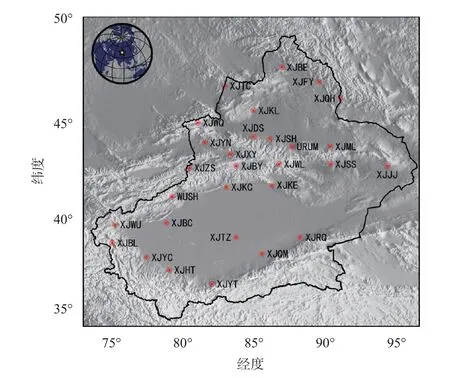
图 1 新疆地区GNSS站点分布

2.1 数据预处理

原始时间序列通过粗差剔除、阶跃项改正、数据插值等预处理工作，获得“干净”的GNSS残差时序.本文采用三倍四分位法进行粗差剔除，选用克里金卡尔曼滤波算法(KKF)对缺失数据进行插值[12]，利用最小二乘拟合去除趋势项，得到残差时间序列[13]. 图2给出了XJQH站预处理后的残差时间序列，黑点为插值效果，蓝点为原始残差序列. 由图2可知，经预处理后，测站坐标时序的粗差、周期项得以有效消除，较真实地还原出缺失数据.

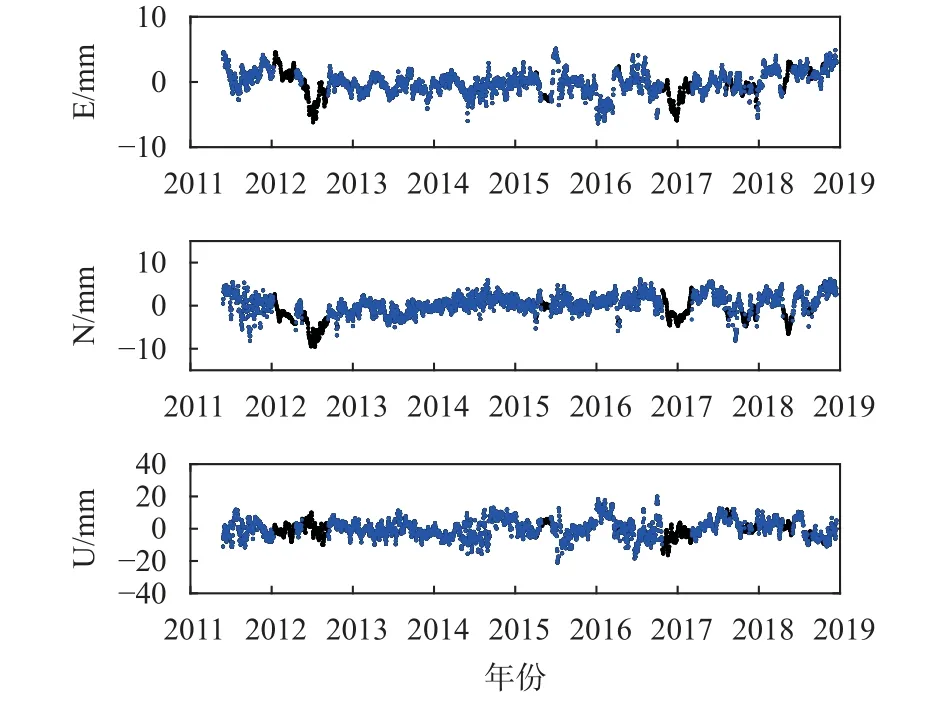
图 2 XJQH站预处理后的残差序列

2.2 共模误差的提取

2.2.1 PCA滤波

对经预处理后的GNSS残差时间序列进行PCA滤波，计算出N、E、U三个方向分量的PC1的贡献率分别为59.91%、64.34%、69.95%，前三个分量的累计贡献分别为79.11%、77.92%、83.52%. 各站点的N、E、U三个方向分量均在PC1所对应的空间响应上表现出一致性，故本文采用PC1提取区域网的CME.

根据式(5)对各测站进行CME提取并剔除，图3(a)给出了经PCA滤波剔除CME前后XJSS站残差时序变化，绿色为原始GNSS残差时间序列，蓝色为经PCA滤波后的残差序列. 由图3(a)可知，经PCA剔除CME后，测站残差时序的离散程度明显降低；XJSS站的E、N、U三个方向分量的残差时序均方根(RMS)值分别降低了58.04%、58.87%、59.56%，PCA滤波后的N、E、U三个方向的残差序列的平均RMS分别减少了42.44%、46.14%、48.94%，显著提高了测站时序信号的信噪比.

图3(b)为经ICA滤波剔除CME前后XJSS站残差时序变化，绿色为原始GNSS残差时间序列，蓝色为经过ICA滤波后的残差序列，与PCA滤波后得到的结果大致相同，测站残差时序的离散程度也明显降低，XJSS站的E、N、U三个方向分量的残差时序RMS值分别降低了45.55%、43.28、47.42%，ICA滤波后残差序列的平均RMS分别减少31.83%、32.29%、35.49%.

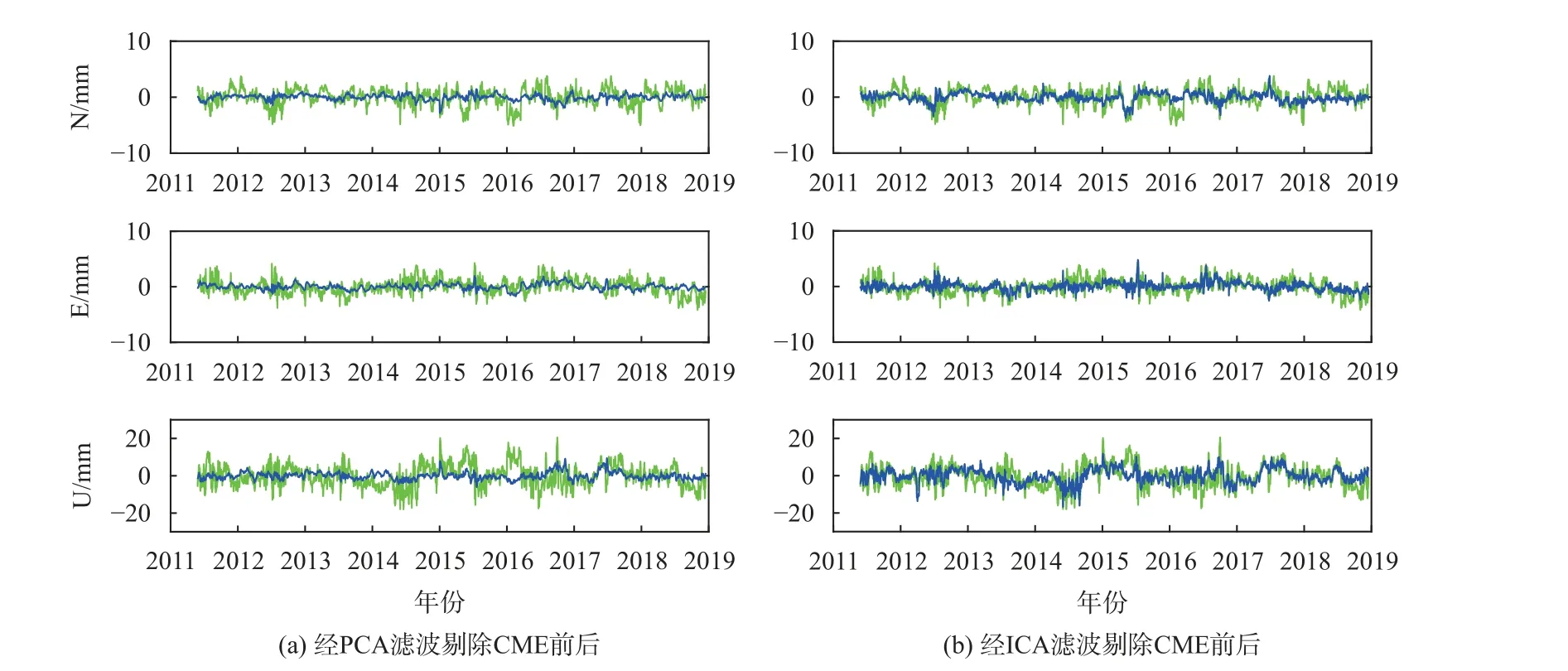
图 3 XJSS站残差时序

2.2.2 ICA滤波

准确选取独立分量是进行ICA滤波的关键，根据式(9)计算出独立分量的贡献比并降序排序，再结合对应的SR来选取恰当的独立分量. 从实验计算结果可分析出，N方向的IC1～IC4、IC6～IC7对应的测站具有一致的SR，E方向的IC1～IC3、IC5～IC7对应的测站具有一致的SR，U方向的IC1～IC6对应的测站具有一致的SR，而其他独立分量的SR无明显的空间一致性. 限于篇幅，本文现给出N、E、U前3个标准化后的独立分量及其对应的归一化SR，如图4所示，红色箭头向上表示空间正响应，蓝色箭头向下表示空间负响应.

由图4可知，IC1在天山区域空间响应较强，在柴达木盆地周围空间响应较弱. 相反，IC3在柴达木盆地周围空间响应较强，在天山区域空间响应较弱.这可能与地表质量荷载有关. 而各测站在IC2上呈负响应，且响应程度较强，其他空间响应呈现出较均匀的强度，具体原因后续将进一步讨论. 根据式(10)计算出各分量的CME，再将具有一致SR的ICA分量进行累加计算得到各测站的CME.

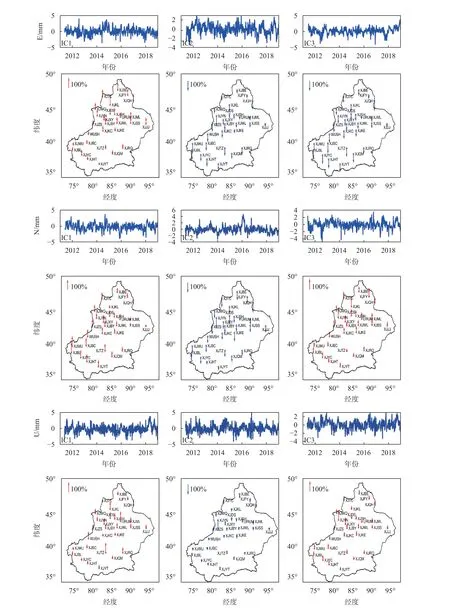
图 4 N、E、U方向分量前3个独立分量及其归一化SR

表1统计了经PCA、ICA滤波后的测站残差时 序RMS值，其经ICA滤波后的测站残差时序的RMS值不如PCA滤波后的结果，这是因为ICA能够最大化非高斯分量，把异常信号当成独立的分量分离出来，使得异常信号能够和CME分离. 而PCA是利用二阶统计量将输入信号分解成方差最大分量来提取CME，存在异常信号被作为CME成分剔除，一定程度上影响CME提取的准确度.

表 1 PCA、ICA滤波前后残差序列的平均RMS变化 mm

3 讨 论

3.1 CME对GNSS测站时间序列的影响

为了探讨CME对GNSS测站时间序列的影响，经探测识别剔除异常信号，选用白噪声+幂律噪声(WN+PL)组合模型[14-15]进行时间序列分析. 图5为经ICA滤波前后测站速度场不确定度变化. 经ICA滤波剔除CME后，N、E、U三个方向分量的速度不确定度分别减少44.14%、38.49%、43.32%，说明ICA能够降低测站时间序列的不确定性，从而提高GNSS坐标序列的可靠性.

图6～7为经ICA、PCA滤波后得到的新疆区域的水平和垂直速度场. 从图6～7可以看出，在水平方向上，新疆地区整体运动趋势以E方向为主，天山东部及准噶尔盆地的运动趋势为E方向，新疆塔里木盆地为NE方向的运动趋势，最大速度为WUSH站，达到33.7 mm·a-1，其总体运动速度由西向东逐渐减弱. 在垂直方向上，大多数测站运动速度小于2 mm·a-1，最大抬升为XJKL站，达到5.8 mm·a-1，经查阅资料，该地区主要是由于油田注水导致了该站出现异常抬升[16]. 天山地区整体上呈现出抬升的趋势，塔里木盆地北部、中部及准噶尔盆地呈现下降趋势. 但这两种方法在天山地区的XJYN、XJXY测站、塔里木盆地南缘的XJHT、XJYT及盆地中部的XJQM测站呈现相反的运动趋势. 通过查阅相关文献，天山地区受盆地挤压而产生抬升的运动趋势，与ICA滤波后的结果一致.

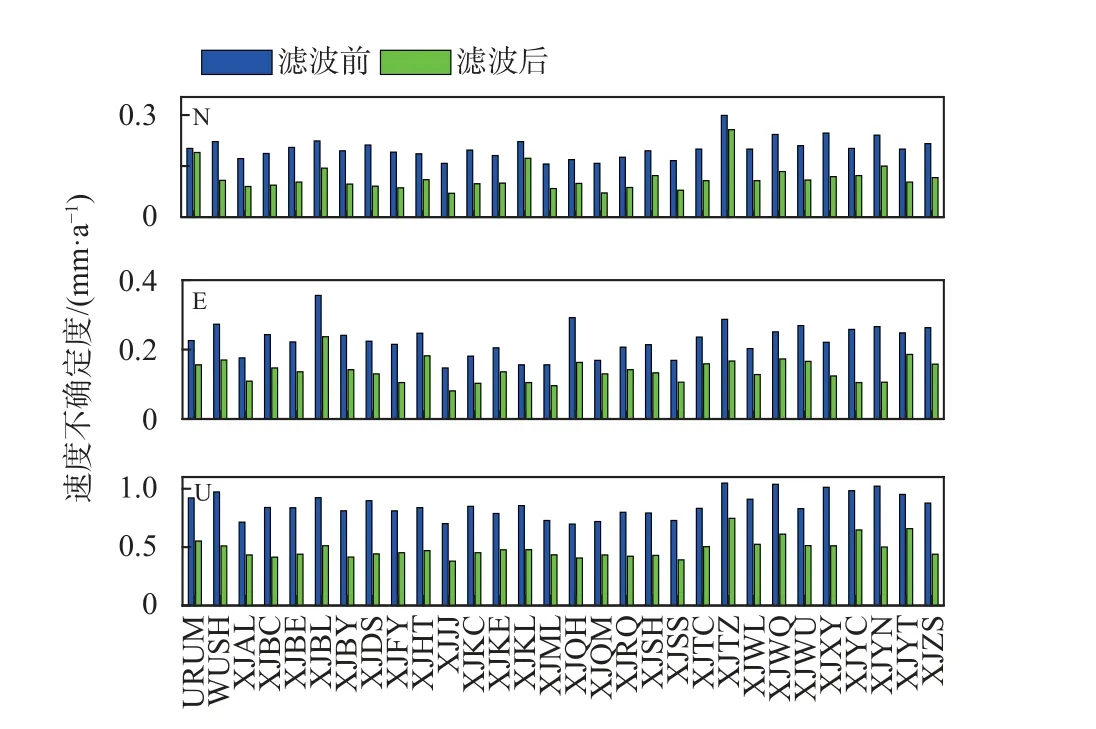
图 5 ICA滤波前后测站速度场不确定度变化

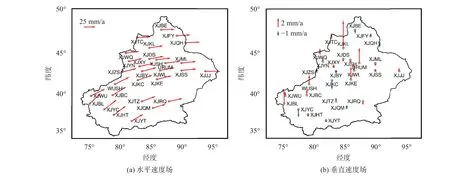
图 6 经ICA滤波后新疆区域水平和垂直速度场

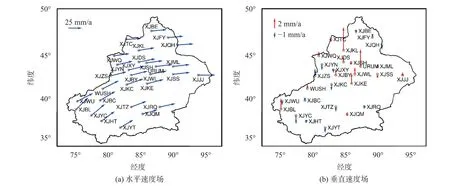
图 7 经PCA滤波后新疆区域水平和垂直速度场

3.2 CME对GNSS测站周期项的影响

GNSS坐标时序中存在明显的周期特性[17]，通过计算得到剔除CME前后测站时间序列的基本参数，如图8所示. 由图8可知，除个别测站外，经ICA滤波后其测站N、E、U三个方向分量的年振幅基本约在1 mm、0.5 mm、3 mm，且测站垂直方向的年周期项振幅高于测站水平方向. 对ICA滤波前后测站的振幅进行对比，可发现绝大多数测站经滤波后其振幅较滤波前更具有一致性，表明CME会影响季节项振幅的估算，得到不准确的物理参数信息. 表2统计了滤波前后测站的年振幅、半年振幅的标准差变化，可以发现剔除CME后测站坐标时间序列参数估计的不确定度有了显著的下降，且N、E、U三个方向坐标分量的年振幅标准差分别减少44.49%、32.89%、43.12%，半年振幅标准差分别减少45.33%、33.07%、43.18%，表明CME对测站坐标时序振幅有较大的影响.

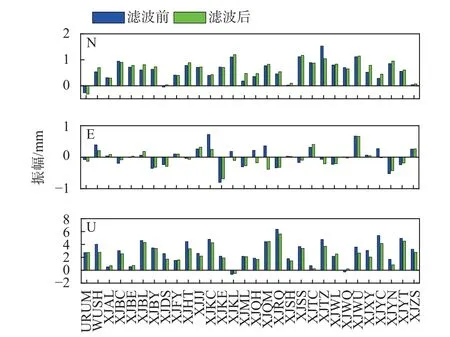
图 8 ICA滤波前后年振幅变化统计图

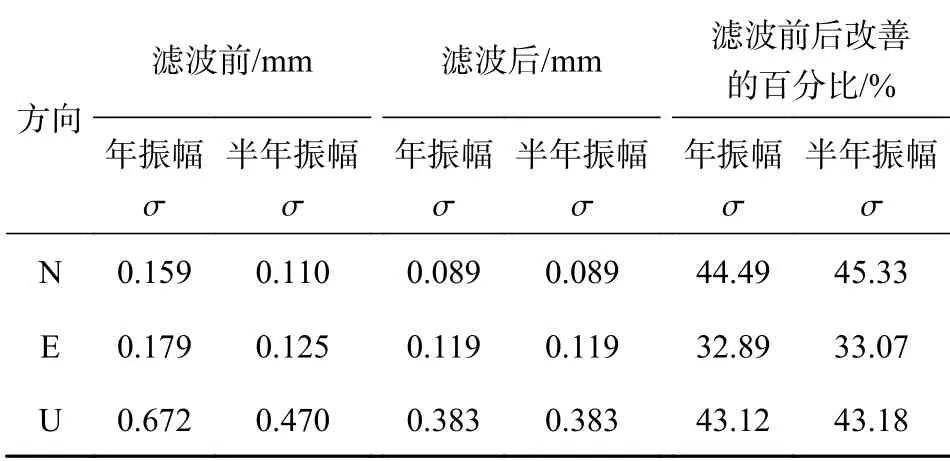
表 2 测站振幅标准差统计

3.3 CME的周期分析

CME是区域内大部分测站都存在的多种时空相关的误差集. 为了对CME内的各种误差信号进行分离，本文使用集合经验模态分解(EEMD)对CME序列进行分解，再采用快速傅里叶变换(FFT)对分离的序列进行周期探测[18]. 通过EEMD计算出IMF1～IMF3为噪声序列， I MF4～IMF7为有效成分，其中IMF6分量具有明显季节性周期变化规律， I MF7分量呈现出明显年周期变化规律，说明CME是一种与时间相关的误差. 图9给出U方向 I MF4～IMF7分量分析结果. 为了直观准确分析周期变化，对EEMD分解后的IMF分量进行了FFT周期探测，如图10所示.功率曲线表现出先增后减的变化趋势，最大值分别在56.3天、83.6天、276天和345天. 说明CME具有半季节性、季节性、半年及年的周期变化规律，这些周期可能是由于参考框架、地表质量荷载、钟差以及未建模的卫星轨道等不确定性因素导致的[19-21]，具体成因还需要进一步的研究和探讨.

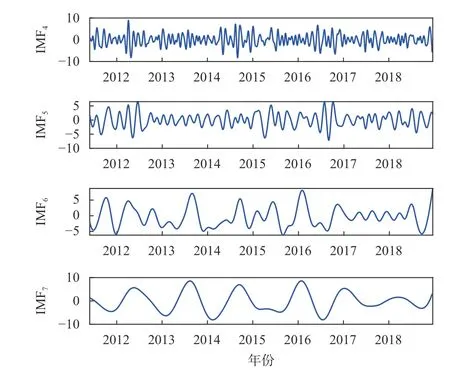
图 9 U方向CME序列的EEMD分解

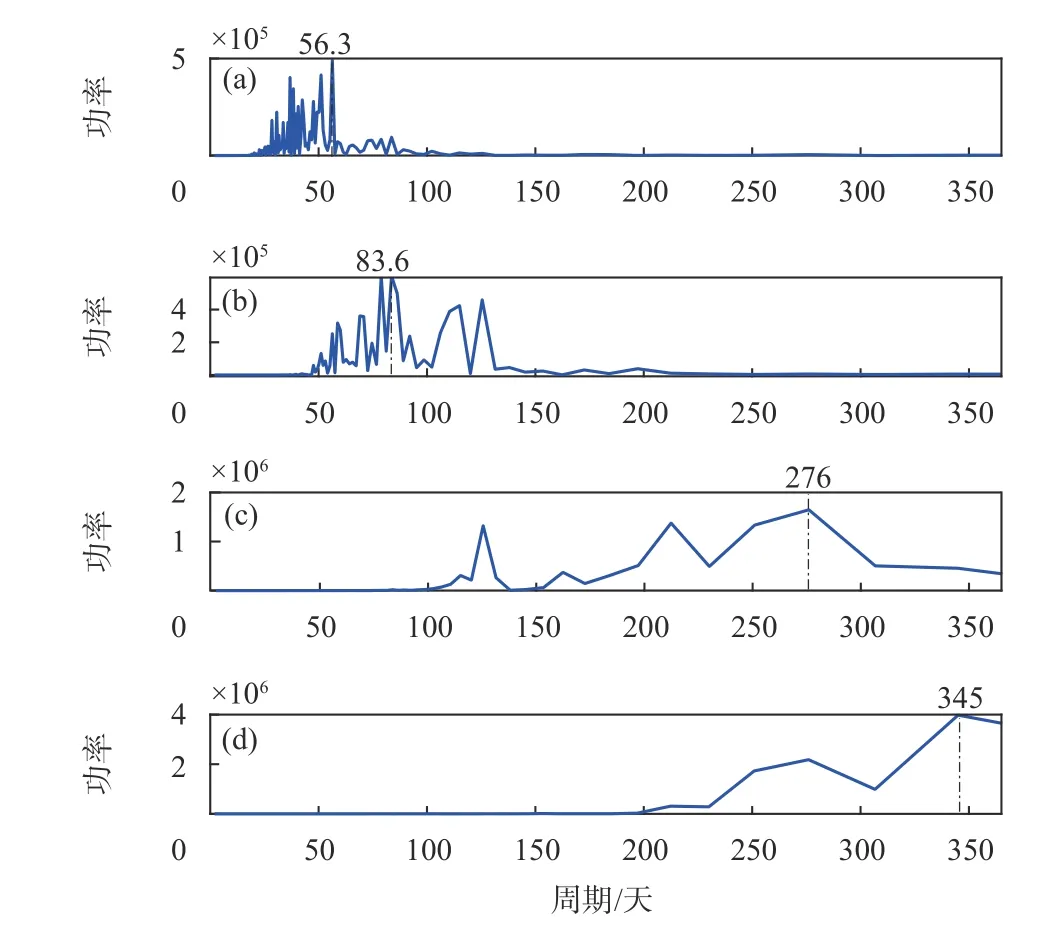
图 10 经EEMD的CME序列的FFT周期探测

针对PCA提取CME时，存在异常信号被作为CME成分的问题，采用ICA方法对新疆地区的GNSS坐标时间序列进行空间滤波，并与PCA的滤波结果进行验证. 发现RMS值均有大幅下降，说明两种方法均能有效提取CME，而ICA能从观测数据中分离出混合的潜在成分和来源，能提取出更准确的CME信号.

4 结束语

通过采用ICA方法进行空间滤波，测站时间序列的速度不确定度、年周期、半年周期振幅标准差均有明显下降，滤波后绝大多数测站的振幅较滤波前更具有一致性，说明ICA滤波能够有助于提高测站时间序列的参数估计的精度.

经ICA滤波后，新疆地区在水平方向整体以E方向的运动趋势为主，总体的运动速度由西向东逐渐减弱. 在垂直方向上，天山地区为抬升趋势，塔里木盆地北部、中部及准噶尔盆地呈现下降趋势. ICA滤波后同时在对CME进行周期性分析时发现，CME具有半季节性、季节性、半年周期及年周期变化规律，产生这些周期的具体成因还需要进一步的研究和探讨.

致谢：感谢中国地壳运动观测网络(CMONOC)提供的GNSS坐标时间序列数据.