面向北斗单历元分米级定位的ARAIM保护水平计算方法

魏依然，郭将，方书山

( 1. 武汉大学卫星导航定位技术研究中心, 武汉 430079；2. 新疆测绘科学研究院, 乌鲁木齐 830002 )

0 引 言

导航对信息化时代有着重要价值，不依赖参考站的精密单点定位(PPP)方式更是因其有效便捷的优势发挥着重要作用，然而实时应用中单点定位很难达到瞬时高精度效果，收敛到厘米级需要数分钟甚至数十分钟. 北斗多频率信号的出现配合瞬时分米级单点定位算法，能够在单历元达到分米级定位精度，极大地方便了PPP的工程应用价值[1]. 但是，单历元分米级定位也面临着宽巷模糊度固定不正确、卫星中断、信号失锁以及多路径效应等众多影响与干扰，因此需要对定位结果的有效性进行评估.

自1987年接收机自体完好性监控(RAIM)提出以来[2]，RAIM逐渐成为航空领域使用全球卫星导航系统(GNSS)服务时的重要监测手段. 随着GNSS的进一步发展和完善，美国演化架构小组(GEAS)在2010年提出了高级接收机自主完好性监测(ARAIM)的架构，以解决GNSS多系统多频率现状下对精密进近提供导航支撑的完好性监测问题[3]，2015年ARAIM基础算法基本完善[4].

ARAIM算法可以计算用户当前历元的保护水平(PL)，它反映了在一定的风险要求下用户定位误差最小置信区间的上限[5]，根据系统设计、长期运行的数据积累分析等方法给定了告警限值(AL)后，就可以通过判断PL是否小于AL来评估当前历元定位的有效性. 因此，我们可以用ARAIM进行分米级单点定位结果的质量评估. 但是，使用ARAIM算法计算得到的PL偏大(通常为十几米至数十米)，使得PL大于AL情况较多，不能反映真实的定位质量，难以满足分米级甚至厘米级用户的质量控制需求. 因此，如何保证在满足风险要求的情况下得到更加合理的PL成为了需要解决的问题[6-12].

本文利用单历元分米级定位所得到的三频无电离层相位组合后验残差结果，针对性地修改了ARAIM 算法中卫星的权与误差模型，提出了一种改进的ARAIM PL算法，为便捷本文统一称其为BARAIM (Back Advanced Receiver Autonomous Integrity Monitoring). 使用ARAIM算法和B-ARAIM算法分别计算用户PL，评估B-ARAIM算法对PL计算的改进情况以及导航的可用性提升情况.

1 单历元分米级和B-ARAIM

北斗多频信号可提供较长波长的组合观测值，通过多频PPP宽巷模糊度固定(PPP-WAR)来即时固定模糊度，可以实现单历元分米级定位[13]. 然后对每个历元的定位情况，可以通过B-ARAIM算法来量化GNSS的导航风险，计算每个历元的PL对定位质量进行初步评估. 首先我们给出单历元分米级定位的观测模型与模糊度固定方法.

1.1 单历元分米级定位

基于原始观测数据的用户端GNSS三频PPP模型表示为

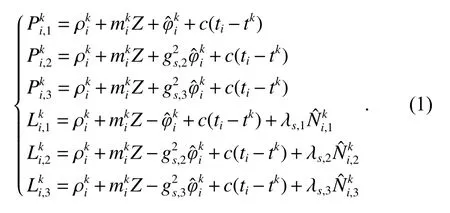
式中：(j=1,2,3) 为 测 站i和 卫 星k之 间 的 频 率j上的伪距观测值；Lk i,j(j=1,2,3) 为测站i和卫星k之间的频率j上的载波相位观测值；为相应的测站和卫星间距离；Z为天顶对流层延迟；为其斜路径映射系数；为一阶电离层延迟；(j=2,3) 是与卫星星座和频率相关的比例系数，其中s为卫星星座标记；ti和tk分别为接收机端和卫星端的时钟误差；(j=1,2,3)为三频吸收硬件延迟后的浮点模糊度；λs,j(j=1,2,3)为对应的三频波长.

由式(1)可知，为了求解测站坐标，需要确定三频的整周模糊度，为此，PPP-WAR首先计算了各系统卫星的小数偏差改正数(FCB)，然后通过式(2)中映射函数将式(1)中的浮点模糊度转换成宽巷和超宽巷模糊度，最后按照式(3)所示利用FCB产品恢复这些宽巷模糊度的整数特性.

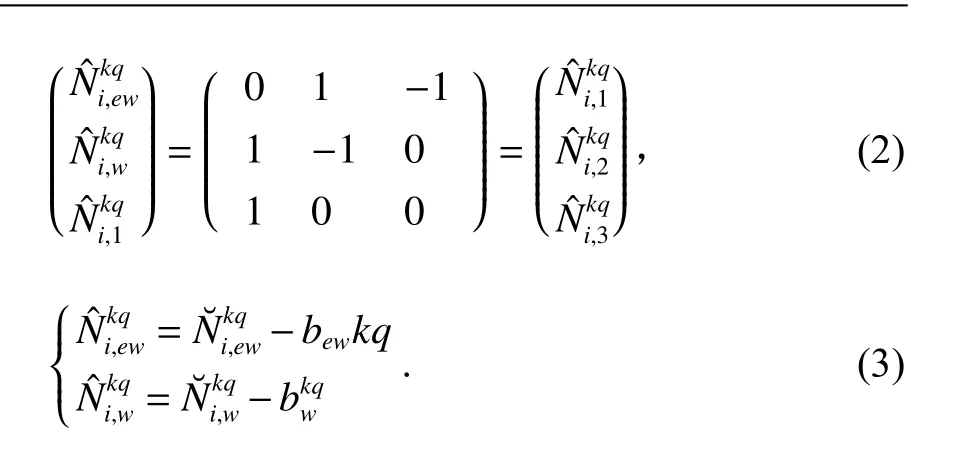
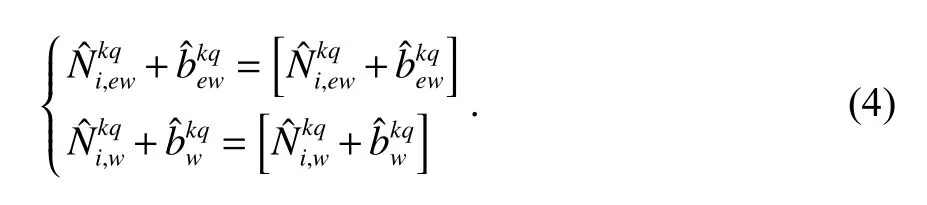
1.2 PL

ARAIM通过多元假设解分离(MHSS)算法来量化GNSS的导航风险[3]，通过完好性支持信息(ISM)中播发的卫星先验故障概率以及星座先验故障概率进行故障模式分类，得到总的故障模式N[15]，为满足导航的完好性需求，有

式中：N为总得故障模式；PHi为第i个故障模式发生的概率；P{(|Δx|＞PL,Di＜Ti)|Hi} 为在i故障模式下，定位误差 Δx大于PL的概率；Di和Ti分别为检验统计量和检验统计门限，所有故障模式造成的完好性风险总和应小于危险误导概率(PHMI).

对于式(5)中的 ( |Δx|＞PL,Di＜Ti) 可变形为

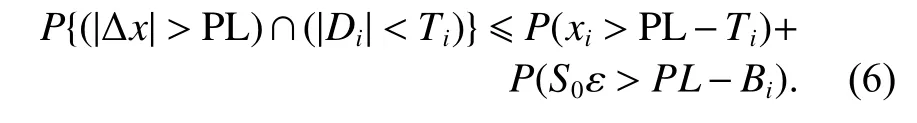
式中： ε 表示随机的测量误差；Bi表示第i个故障模式对定位结果可能造成的最坏影响，可由完好性支持信息播发和定位法方程的系数矩阵计算得到. 进一步对式(6)进行变形，结合式(5)可得到PL的一个上界值

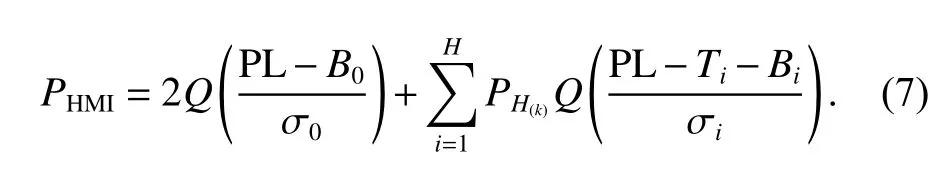
式中： σi表示第i个故障模式的定位结果的标准差；Ti由第i个故障模式与全卫星集合定位结果差值的标准差计算得到. 因此，利用式(7)即可求解当前历元的垂直保护水平(VPL)和水平保护水平(HPL). 由式(5)可知PL反映了当前完好性风险要求下用户定位误差最小置信区间的上限. 同理，垂直用户PL和水平用户PL分别是指满足完好性风险要求的垂直定位误差和水平定位误差的最小置信区间的上限[5,16-21].对于B-ARAIM算法，利用后验的权与误差模型，计算新的Ti与 σi，对PL结果进行改进，下面介绍用于B-ARAIM算法的权与误差模型.

1.3 权与误差模型

传统ARAIM算法将误差模型定义为用于完好性的标称误差模型Cint(i,i)和用于连续性及准确性的标称 误 差 模 型Cacc(i,i)，并将权定义为W(k)(i,i)=(i,i) .误差模型如式(8)所示，其中和均表示卫星端误差，主要是卫星钟差及星历误差导致的误差，是用于 精度和连续性的模型，而用于完好性模型，其较更为保守，一 般 是的1.5倍；表示传输端误差，传统ARAIM算法使用双频无电离层观测值，因此主要是通过经验值先验的对流层误差；表示用户端的误差，主要由经验值先验的接收机噪声和多路径引起[4].

本文采用单历元分米级的定位结果对权与误差模型进行后验改正，在PPP-WAR解算过程中，使用精密轨道和钟差后，基于卫星钟差及星历误差的和将显著减小，新的使用国际GNSS服务(IGS)给出的精密产品精度来确定[22]，设为的1.5倍. PPP-WAR采用了一种三频无电离层组合进行计算，在普遍情况下都消除了电离层误差. 文献[23]给出了详细的推导和公式，同时使用精密对流层模型并估计残余对流层误差，可以假定传输端的误差都已被修正. 需要注意的是，本文主要目的在于研究适合PPP分米级定位的PL计算方法，对极少数电离层扰动以及高阶电离层的影响等更精细的风险予以忽略. 多路径误差和观测值噪声部分体现在残差结果中. 此外，由于错误固定的模糊度很难被直接识别出来(即使通过了Ratio检验)，但其会对定位结果及残差造成显著影响，因此模糊度固定风险可以通过定位结果风险来体现. 最终B-ARAIM的误差模型如式(9)所示[24].表示由多系统的三频无电离层模型进行的残差组合，表1介绍了无电离层使用不同频率组成该三频时的系数[1].

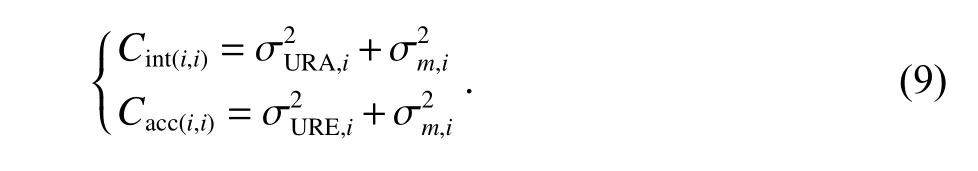
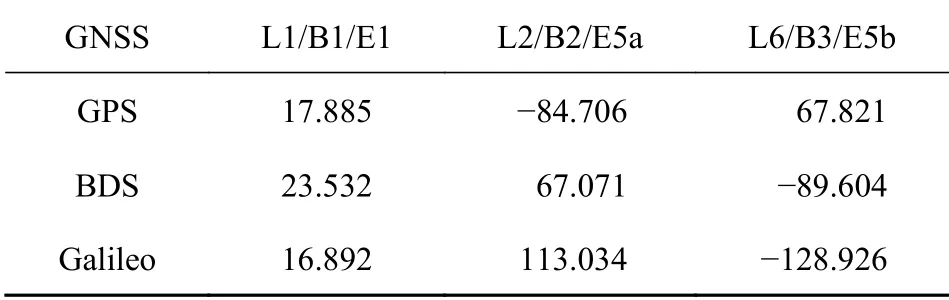
表 1 无电离层三频模型系数

因此，整体而言，图1为B-ARAIM的算法流程.

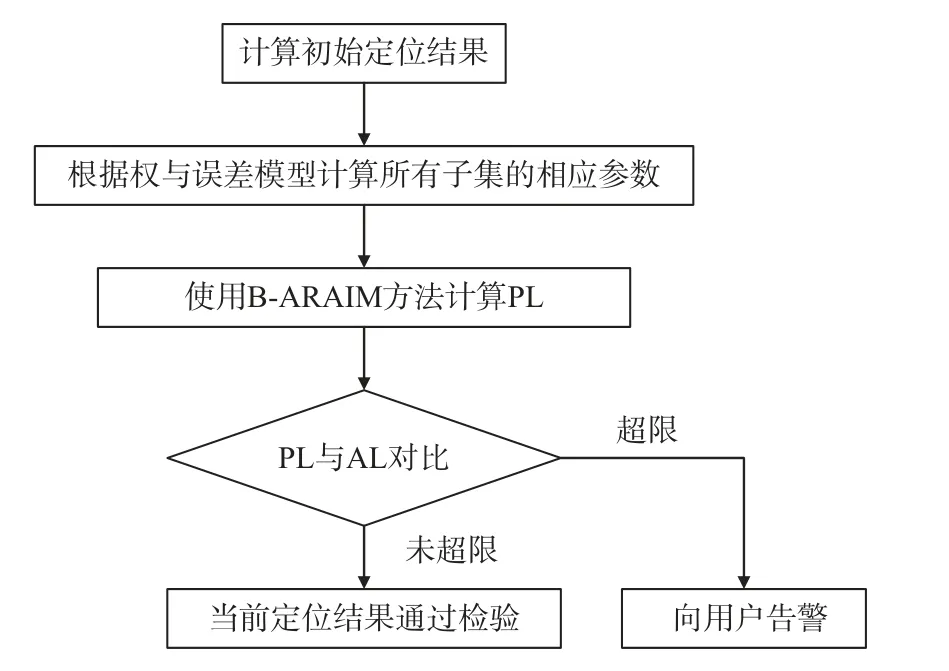
图 1 B-ARAIM整体流程

2 实验与验证

为验证本文用于单历元单点分米级定位质量评估的改进ARAIM PL算法的效果，选取了不同场地进行车载实验来验证. 在车顶安置接收机天线，对观测数据进行仿实时处理，使用实时动态(RTK)结果作为参考真值，使用自编程序分别计算基于ARAIM算法和B-ARAIM算法的PL. 在空旷地带和城市峡谷地区分别开展实验，验证导航用户可能面临的不同环境下使用PPP-WAR进行导航时，B-ARAIM算法对PL计算的改进情况以及导航的可用性提升情况.

2.1 PL

车载实验一位于湖北省武汉市楚河汉街区域，图2(a)显示了2018年3月2日的行车路线图(由Google Earth生成). 图2(b)显示了实验路线的周边区域信息(由百度地图生成). 由图2可知，实验所在区域高楼较多，卫星信号遮挡严重.

图 2 2018年3月2日车载实验一路线图和环境示意图

图3比较了使用传统ARAIM算法和使用BARAIM算法计算得到的HPL和VPL. 在整个实验过程中，由于大部分历元的卫星数都难以满足单系统导航的要求，因此仅计算了GPS、北斗卫星导航系统(BDS)及Galileo多系统导航的结果. 由图3可知，由于传统ARAIM算法和B-ARAIM算法都没有使用历史观测值，受到当前历元的观测值的影响较大，因此由于观测环境较差导致卫星信号中断等原因，实验中一度因卫星信号完全中断而没有结果. 需要声明的是，卫星不足、信号中断等情况可通过粗差探测识别出来，但为了验证B-ARAIM算法能否识别这种情况，我们也将这部分结果保留了下来. 由图3可知，整体而言使用B-ARAIM算法在保证了所有历元PL不小于定位误差. 同时无论在水平还是垂直方向上都有超过98%的历元计算得到的PL值都小于传统ARAIM算法得到的PL，使用B-ARAIM方法计算得到的PL减小了约30%. 由B-ARAIM方法计算得到的PL与定位结果的一致性也更高，这是因为PPPWAR方法使用高精度产品和模糊度固定后的相位组合观测值进行定位，基于B-ARAIM方法建立的误差模型更能反映其定位情况.

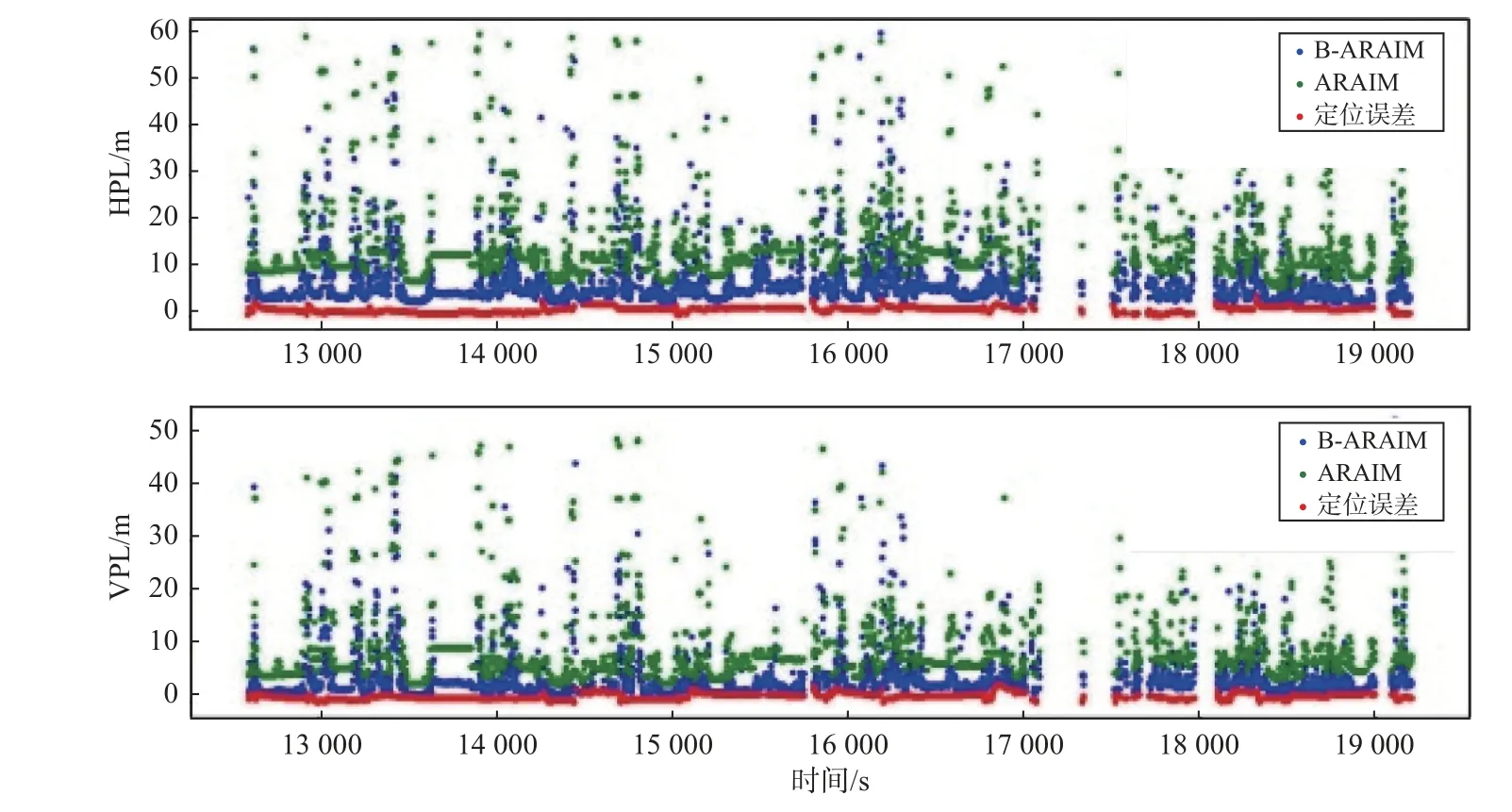
图 3 车载实验一的水平(上)和垂直(下) PL时间序列图

车载实验二位于湖北省武汉市江夏区左家村区域，图4(a)为2018年6月27日的行车路线图(由Google Earth生成)，图4(b)为了实验路线的周边区域信息(由百度地图生成). 由图4可以看出，实验所在区域较为空旷，卫星信号接收较良好.

图 4 2018年6月27日车载实验二路线图和环境示意

图5比较了基于多系统导航的传统ARAIM算法和B-ARAIM算法计算得到的相应的HPL和VPL.图6比较了基于单北斗系统的传统ARAIM算法和B-ARAIM算法计算得到的相应的HPL和VPL. 与图3相似，由图5可知，B-ARAIM方法可以在100%的历元保证PL不小于定位误差，并将PL减小了约50%，较实验一中PL减少的更多，这是因为实验二所处的良好观测条件，导致观测结果残差较小. 同时，多系统导航结果与单北斗系统结果中所有历元，BARAIM算法计算得到的HPL和VPL都要小于传统ARAIM算法得到的PL.

对比图3和图5～6可以看出，实验二所得到的PL连续性较实验一更好，PL的时间序列更加连续，特别是使用单北斗系统时，HPL和VPL都表现为一条连续的曲线. 这是因为当实验处于开阔地带时，卫星信号更好. 图7展示了两次实验中接收到卫星的数量情况.

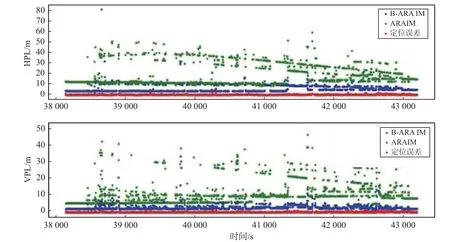
图 5 车载实验二的水平(上)和垂直(下)PL(多系统)时间序列图

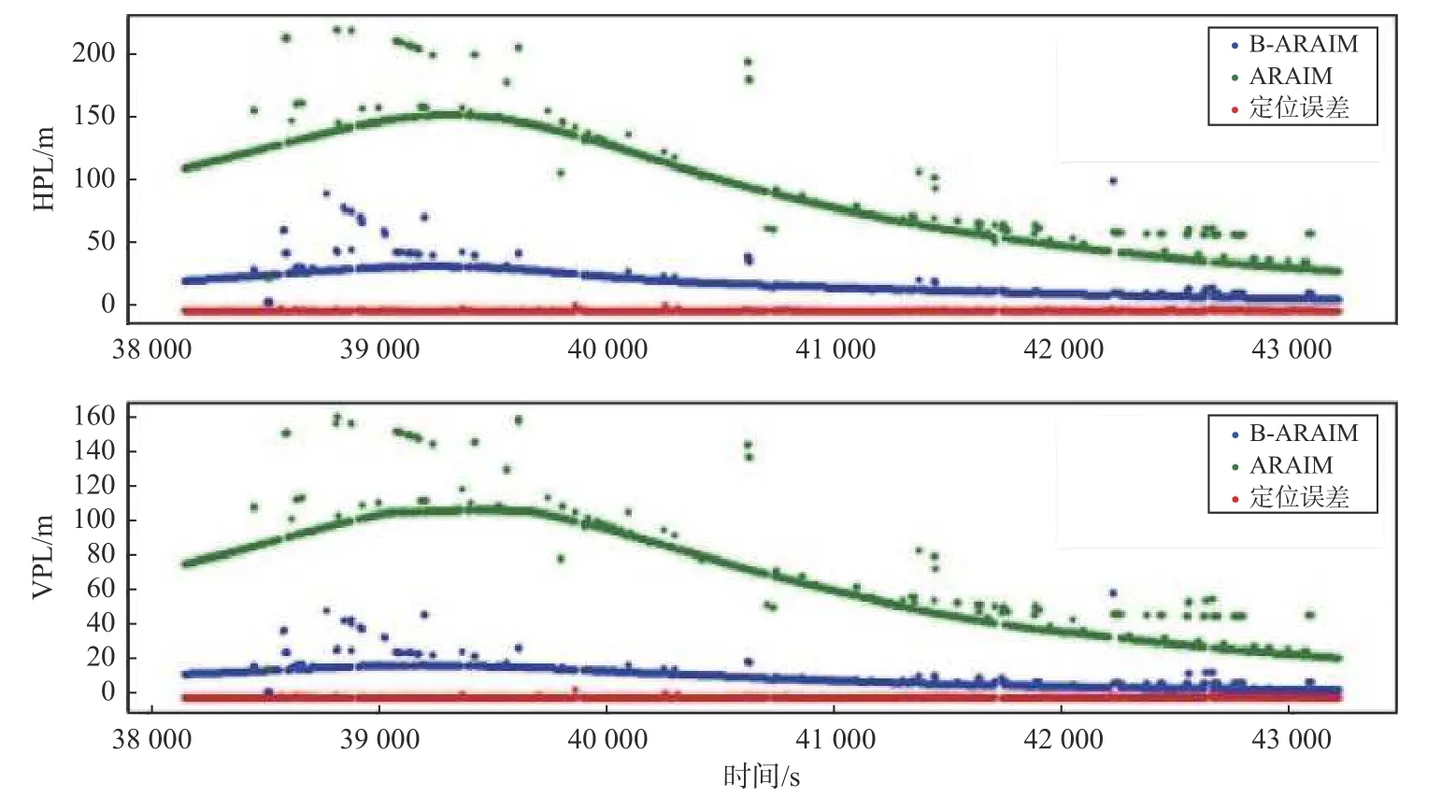
图 6 车载实验二的水平(上)和垂直(下)PL(单北斗)时间序列图

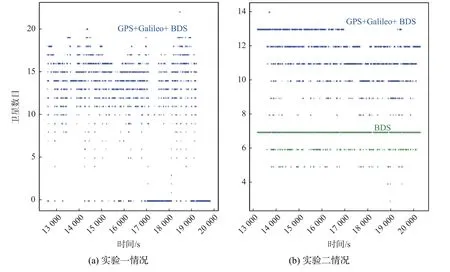
图 7 车载实验二观测卫星数目

图8比较了实验一和实验二中所得到的PL的差值，将传统ARAIM算法和B-ARAIM算法计算得到的PL差值用作评估新方法的改进情况. 可以看出，当卫星信号稳定时，PL的改进效果更加明显；当卫星信号较差时，约2%的历元会出现B-ARAIM算法求得的PL大于传统ARAIM算法求得的PL的情况. 这是因为在GNSS覆盖不足地区，由于多路径、卫星数过少等原因会导致造成某些历元星残差过大，甚至远远超过伪距标称误差. 由图6可知，当单北斗系统卫星数较少时，所求得的PL会很大，基于传统ARAIM算法35%的历元HPL都在100 m以上，50%历元的VPL在60 m以上，但是从图8(c)可以看出，当卫星数较少时，即使用单北斗系统时B-ARAIM算法计算得到的PL改进效果更加明显，PL减小了约60%～70%. 使用B-ARAIM算法的改进效果更加明显是因为当卫星几何构型较差时，基于传统ARAIM算法的保护水平增长得的更快.

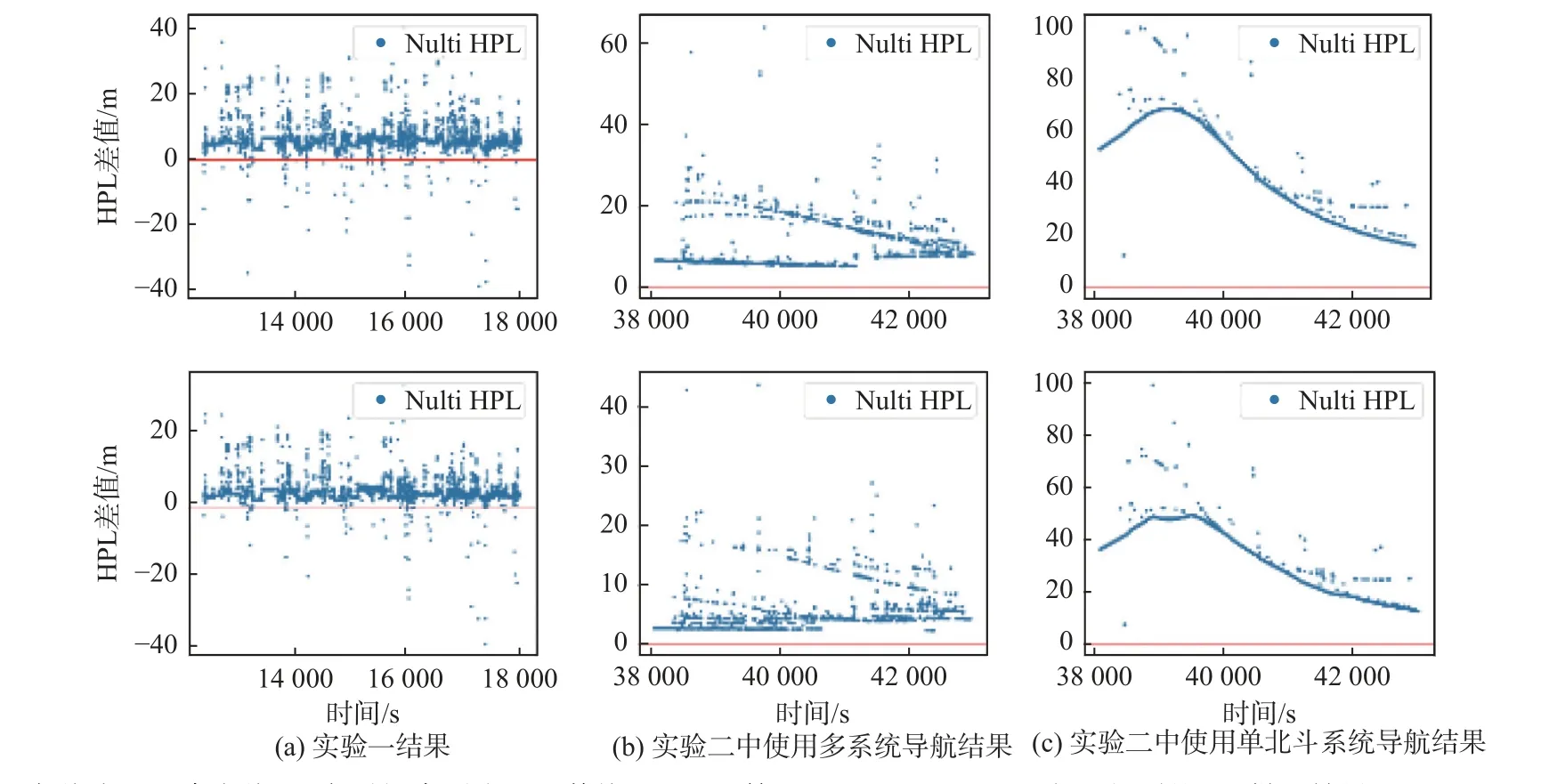
图 8 车载实验一及实验二PL差值

2.2 可用性

利用ARAIM算法评估高精度定位质量时，通过比较PL和AL来判断，当PL＞AL时定位结果是有风险的，弃用这些历元会影响导航的可用性，因此需要对导航的可用性进行检验，以评估使用B-ARAIM替代ARAIM进行高精度定位质量控制的改进情况. 因AL的选取一般需要相关协会出台相关文件做出要求，但是对于车载导航的AL要求一直没有一个统一的规定. 鉴于此本文使用飞行导航LPV-200(localizer performance with vertical guidance-200 feet)精密进近所使用的AL标准来评估B-ARAIM算法对可用性的影响情况，将VAL设为35 m，将HAL设为40 m[5].

图9～10分别显示了实验一及实验二中使用多系统和单北斗系统所得到的HPL和VPL的分布情况，表2～3展示了相应的VPL和HPL均值及算法可用历元的情况. 从表2～3中可以看出，仅使用单北斗系统的可用性较低，对于VPL而言，使用B-ARAIM算法仅有不到49%的历元满足要求，使用传统ARAIM算法更是低于18%；对于HPL的结果更差，B-ARAIM和RAIM得到的PL分别只有不到40%和11%的历元满足要求. 尽管可用性都较低，但是B-ARAIM在保证单历元分米级定位质量控制的同时，对导航的可用性有明显提升. 同时可以看出使用多系统导航得到的结果可用性对比单北斗系统有显著的提升；对于VPL和HPL而言，无论是在城市峡谷地区还是空旷地带得到的结果都在96%以上. 在VAL设为35 m及HAL设为40 m的情况，基于多系统导航使用传统ARAIM算法得到的结果已经较好，使用B-ARAIM算法提升不大，但是使用B-ARAIM算法得到的VPL和HPL均值都有明显的减小，这使得B-ARAIM算法更容易满足更小的AL要求以实现可用性. 当针对车载导航的AL确定后，B-ARAIM算法将有利于在保证单历元分米级定位质量控制的同时，提升导航的可用性.

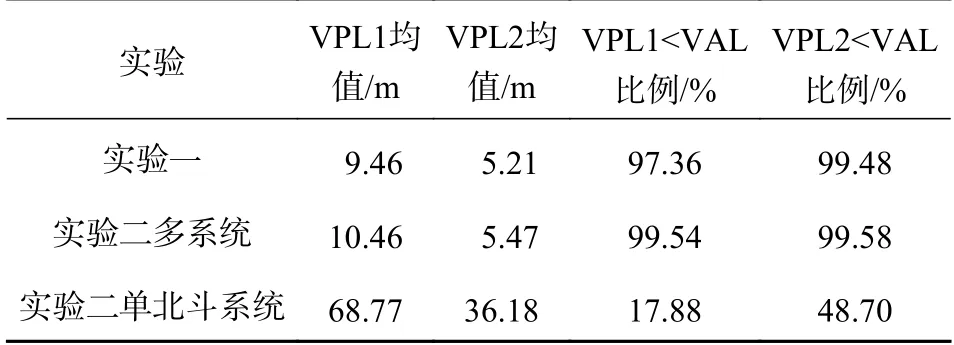
表 3 VPL情况

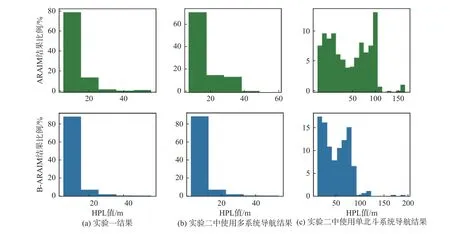
图 9 车载实验一及实验二HPL分布情况

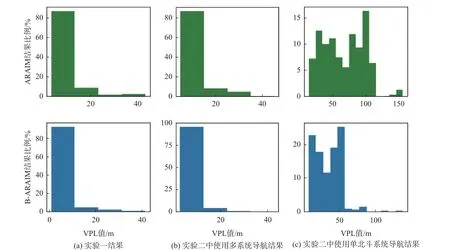
图 10 车载实验一及实验二VPL分布情况

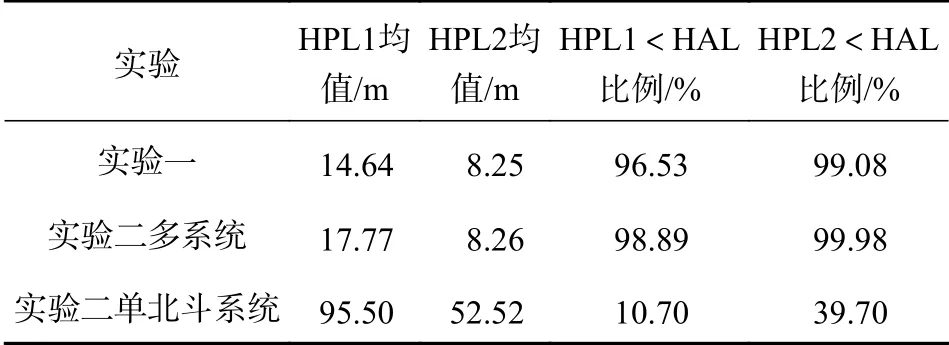
表 2 HPL情况

3 结 论

本文重点研究了基于PPP-WAR使用B-ARAIM算法相较ARAIM算法对PL计算的改进情况，以此对城市环境下的高精度GNSS导航应用进行初步的质量控制. 在城市峡谷地区和城郊空旷地带采集了一次数据对算法进行了验证. 分别对GPS、BDS及Galileo多系统导航和单北斗系统结果进行了评估，得出如下结论：

1)在城市峡谷地区与城郊空旷地带及卫星信号不同的情况下，B-ARAIM算法相较传统ARAIM算法均有一定程度的提升，从图3、图5及表2～3可以看出，使用多系统导航可使PL减小约30%～50%；从图6以及表2～3可以看出，使用单北斗系统可以减小约70%，在大部分历元都有效降低了HPL和VPL，使其更加贴合真实的PPP-WAR定位误差. 在卫星信号较好的地带提升效果更好.

2)使用单北斗系统时，B-ARAIM方法相较传统ARAIM算法提升要更加明显，显著降低了HPL和VPL. 但是，由于使用单北斗系统时卫星数目减少和卫星几何构型变差的影响，使用单北斗系统以满足利用ARAIM评估定位质量的需求，改进后的PL仍然过大，现阶段即使以民航所使用的标准来看都难以达到，更加难以满足车载导航的需求.

3)车载环境的导航条件可能更为极端且严峻，因此B-ARAIM得到的PL相较车载导航预估的AL而言可能仍然偏大，利用ARAIM评估高精度定位质量仍有待进一步的研究.