Helmert方差分量估计在GPS/GLONASS/BDS/Galileo组合精密单点定位权比确定中的应用

李琴，姚顽强，涂锐

( 1. 西安科技大学 测绘科学与技术学院, 西安 710054；2. 中国科学院国家授时中心, 西安 710600；3. 中国科学院精密导航定位与定时技术重点实验室, 西安 710600 )

0 引 言

随着全球卫星导航系统(GNSS)的不断完善与推广，在GNSS导航定位领域，多模GNSS组合受到越来越多人的关注[1]. 目前卫星导航定位的主流系统有[2-4]：美国的GPS，俄罗斯的 GLONASS，中国的北斗卫星导航系统(BDS)与欧盟的Galileo. 采用GPS/GLONASS/BDS/Galileo多系统组合导航定位相较单系统具有时空域覆盖更加广泛的特点，能显著增加可见卫星个数，优化星座分布，从而提高定位的可靠性和稳定性[2].

在卫星导航定位技术中，精密单点定位(PPP)技术由于定位精度高、结构简单、操作灵活(无需任何参考站)，已在许多领域中得到广泛应用，如精准农业、精准测绘、变形监测、水汽反演、精准导航和定位等[5]. PPP是利用卫星的精密轨道和精密钟差信息，综合考虑各项误差改正，联合伪距和载波相位观测进行参数估计，以单台GNSS接收机实现全球高精度(一般可达分米至毫米级)绝对定位的一项技术[6].

PPP待估参数的解算与观测向量的协方差或权矩阵密切相关，准确估计权阵对于实现高质量定位非常重要. 由于信号结构、频率、信噪比和信号传输路径的不同，各系统的观测质量也不尽相同[7]. 因此，组合定位中GPS、GLONASS、BDS和Galileo观测组的权比也需要准确确定. 方差分量估计可以通过不同类型观测组的方差来确定它们之间的权比[8]. 常用的方差分量估计方法有[9]：Helmert方差分量估计[10]、最小范数二次无偏估计(MINQUE)[11]、最佳不变二次无偏估计(BIQUE)[12]、最小二乘方差分量估计(LS-VCE)[13]，约束最大似然估计(REML)[14]. 在这些方差分量估计方法中， Helmert方差分量估计能在每个历元中通过参数估计方法预平差得到残差，基于残差估计各个系统伪距和载波相位观测的验后单位权方差，通过迭代上述过程实时解算各系统间权比. 因此，Helmert方差分量估计定权方法可应用于多星座组合的实时导航定位.

很多学者对Helmert方差分量估计定权方法在GNSS多星座组合定位中的应用作了研究：ZHANG[15]在GPS/BDS组合PPP中，采用了MVCE (Modified Variance Component Estimation)和Helmert方差分量估计相结合的定权方法. 其中， MVCE方法用来调整同一系统内部伪距观测组和载波相位观测组的权重，Helmert方差分量估计方法用来调整GPS观测组和BDS观测组的权重，静态和动态测试结果表明，该方案可显著提高GPS/BDS 组合PPP的定位精度和稳定性，并减少收敛时间. 代阳等[2]将Helmert方差分量估计方法应用于GPS/GLONASS/BDS/Galileo组合伪距单点定位(SPP)中，试验结果表明：采用Helmert方差分量估计定权方法在北(N)、东(E)、高程(U)方向上的定位精度与可靠性均有所提升. 张哲浩等[16]也做了类似研究，通过对比不同随机模型的定位结果，发现在GPS/GLONASS/BDS/Galileo组合SPP中，Helmert 方差分量估计模型能提高定位精度.但目前将Helmert方差分量估计定权方法应用于四系统组合PPP的研究还比较少.

为此，本文在给出GPS/GLONASS/BDS/Galileo组合PPP的函数模型、随机模型和参数估计方法基础上，研究了如何应用基于测量残差的Helmert方差分量估计定权方法来调整GPS、GLONASS、BDS和Galileo观测组的权重，以提高多系统组合PPP的定位性能，最后通过10个IGS测站一周的数据来分析验证本文方法的可行性和有效性.

1 多星座组合PPP

1.1 无电离层组合函数模型

标准双频无电离层组合的观测方程为[15,17]：

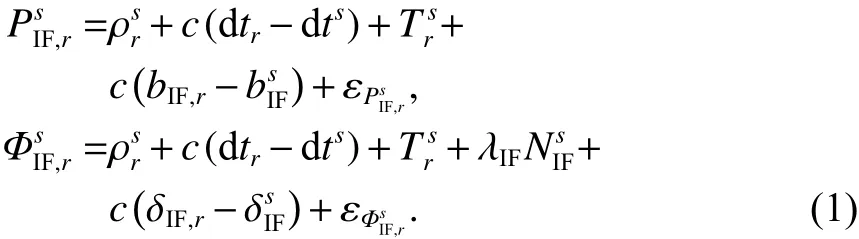
式中：下标r和上标s分别为接收机和卫星；和为无电离层组合伪距和相位观测值；为卫星到接收机之间的几何距离；c为真空中的光速； dtr和dts为接收机钟差和卫星钟差；为对流层延迟；bIF,r和为无电离层组合接收机端和卫星端的伪距硬件延迟； δIF,r和为无电离层组合接收机端和卫星端的相位硬件延迟； λIF和为无电离层组合的波长和模糊度； εPIsF,r和 εΦIsF,r为无电离层组合伪距和相位的观测噪声误差.

通常，导航系统的轨道和钟差产品是用特定信号或信号组合生成的[18]. 例如，对于GPS的导航电文或IGS精密产品来说，卫星钟差都是用由P1(调制在L1载波上的P码)和P2(调制在L2载波上的P码)所组成的无电离层组合生成的. 因此，卫星钟差包括相关组合信号的卫星硬件延迟和实际卫星钟差. 在数据处理过程中，卫星钟差 dts吸收了无电离层组合卫星端伪距硬件延迟，无电离层组合接收机端伪距硬件延迟bIF,r则被接收机钟差 dtr吸收，即：

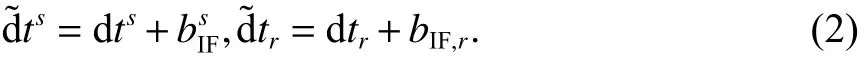
需要说明的是，相位硬件延迟在一段时间内变化幅度极小，所以其会被模糊度参数吸收[19]，即

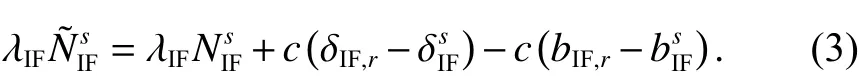
卫星钟差经过精密产品改正后，式(1)可以表示为：

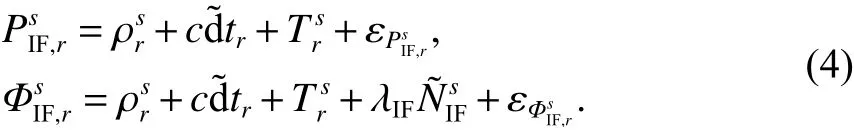
扩展到多星座组合PPP，观测方程可以用下式表示：

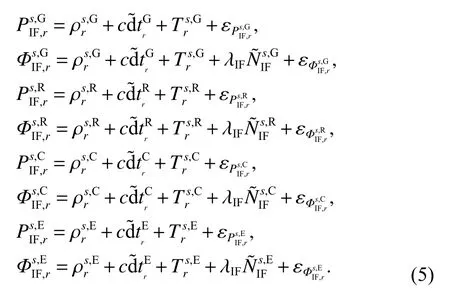
式中：G、R、C、E分别表示GPS、GLONASS、BDS和Galileo系 统；s,G 、s,R 、s,C 、s,E 分 别 表 示GPS、GLONASS、BDS和Galileo系统的某颗卫星. 值得注意的是，部分误差未在上式中列出，如卫星和接收机天线相位中心误差、相对论效应、天线相位缠绕、固体潮、海潮、大气潮，但在数据处理中已对它们进行改正.

待估参数向量可以表示为

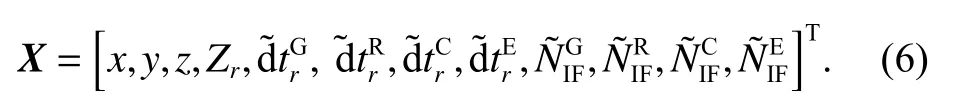
式中：x、y、z表示测站接收机坐标；Zr表示对流层天顶方向湿延迟.

1.2 随机模型

同一卫星导航定位系统的不同卫星观测值定权可基于卫星高度角建立随机模型：卫星高度角与其观测值权重成非线性正比关系，当卫星高度角较低时，其观测值所占权重也应相对较小. 本文采用正弦函数高度角模型来确定伪距和载波相位观测值的权重

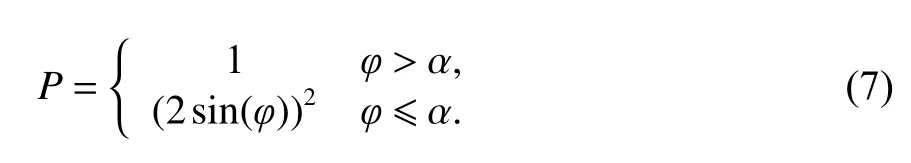
式中：P为某颗卫星伪距或载波相位观测值的权重；φ为该卫星的高度角； α 表示设置的高度角阈值，一般设为30°.

1.3 基于序贯最小二乘的参数估计[20]

设 在tk历 元 有nk×1 观 测 向 量Lk，该 观 测 向 量Lk相应的协方差矩阵为Dk，权矩阵为在tk-1历元，通过参数估计过程获得参数向量估计值Xk-1和相应的协方差矩阵DXk-1. 误差方程为

式中：Vk为Lk的残差向量；Ak为nk×m设计矩阵；Xk为tk历元m×1 参数向量估计值. 由于参数具有先验期望和方差，则参数估计的最小二乘准则为

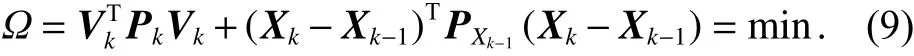
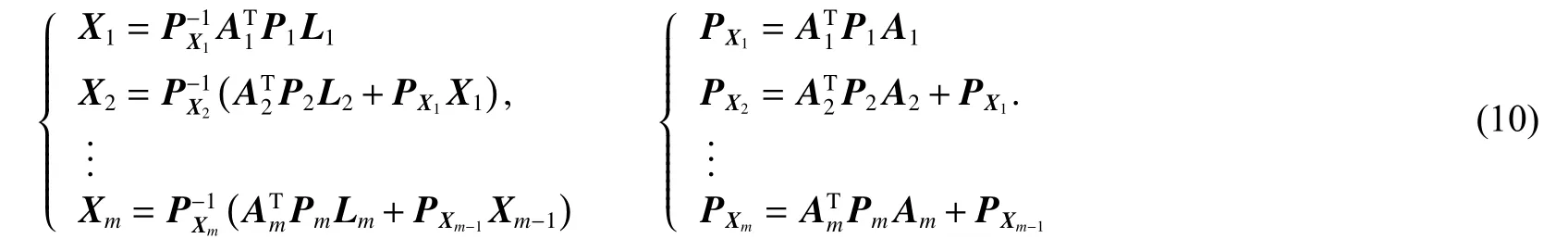
需要注意的是，在使用序贯最小二乘解算待估参数时，法方程具有可加性，所以在参数向量不同维时需要先做矩阵转换.

2 基于方差分量估计的定权方法

GPS、GLONASS、BDS和Galileo四系统的Helmert方差分量估计过程为[21]：

1) GPS、GLONASS、BDS和Galileo四系统的初始权比设置为PG=PR=PC=PE=1 ，同一卫星导航定位系统内部，不同卫星的伪距和载波相位观测通过正弦函数高度角模型定权(详见1.2节)，伪距观测组和载波相位观测组的权比为1∶100.

2)采用最小二乘解算观测方程，并根据误差方程利用解算出的参数向量计算各类系统的残差向量分别为VG、VR、VC、VE.

3)根据严密的Helmert方差分量估计公式，利用解算出的各系统残差计算各个系统的单位权方差

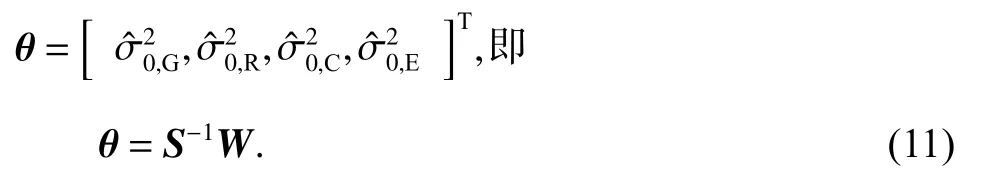
式中各个变量计算如下：

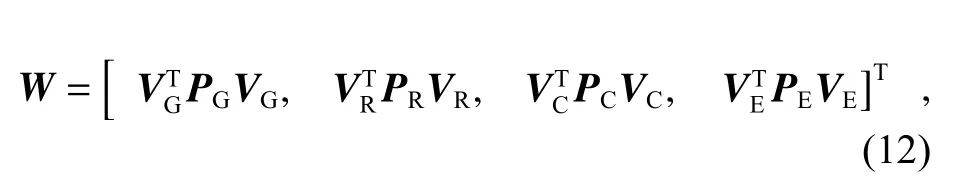
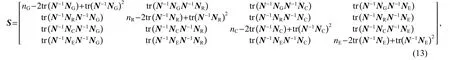
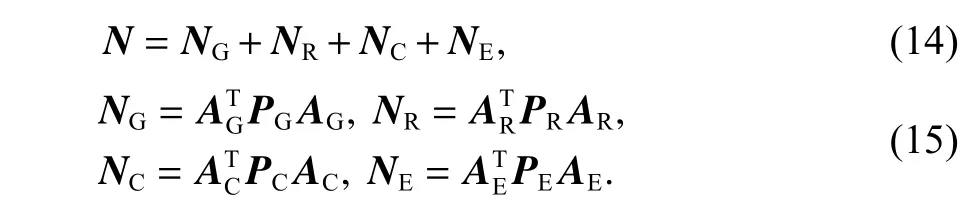
式中，nG、nR、nC和nE分别为GPS、GLONASS、BDS和Galileo系统的观测方程个数.

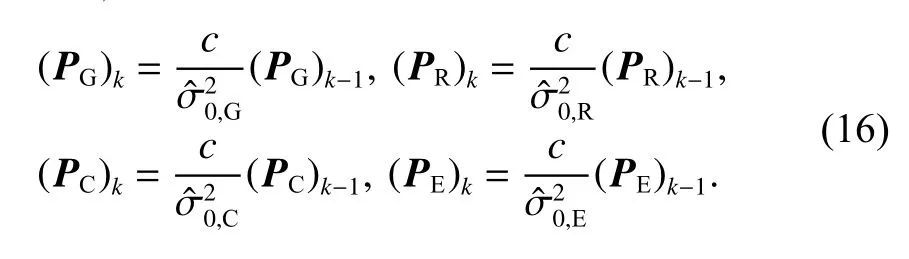
式中：k表示本次计算结果；k-1 表示上一次计算结果；c为一常数；通常取中 的 某 个值，本文取

3 实验、结果和分析

3.1 实验数据

本文实验测试采用IGS MGEX (Multi-GNSS Experiment) 站网10个测站2021年2月8日至2月14日一周的观测数据. 观测文件包括GPS、GLONASS、BDS和Galileo系统的观测数据，采样率为30 s. 选取的测站地理分布如图1所示. 此外，卫星轨道和卫星钟差由GFZ (GeoForschungsZentrum Potsdam)提供.

图 1 IGS站点的地理分布

3.2 数据处理策略

采用团队自编软件进行多星座组合PPP解算，所有定位过程均在静态或动态模式下执行. 表1提供了本研究使用的详细处理策略.

表 1 多星座组合精密单点定位数据处理策略

3.3 Helmert方差分量估计对多星座组合PPP的测试

为了验证Helmert方差分量估计定权方法的有效性，在静态模式下和仿动态模式下对多星座组合PPP进行两种不同的定权方案测试. 第一种是默认的等权定权方案(EQL)，即各系统之间的权比为PG=PR=PC=PE=1. 第二种方案是使用Helmert方差分量估计定权方法计算各系统之间的权比. 在该方案中，当部分历元各系统之间的权比解超过设定阈值时，用初始权比(即等权)代替权比解. 在静态试验中，PPP的定位误差由最后一个历元的定位误差表示，收敛时间设定为E和N方向的定位误差小于0.1 m，U方向的定位误差小于0.2 m，并持续10 min的时间.在仿动态试验中，PPP的定位误差由收敛后所有历元定位误差的均方根(RMS)表示，收敛时间为E、N方向定位误差小于0.2 m，U方向定位误差小于0.3 m，并持续10 min的时间.

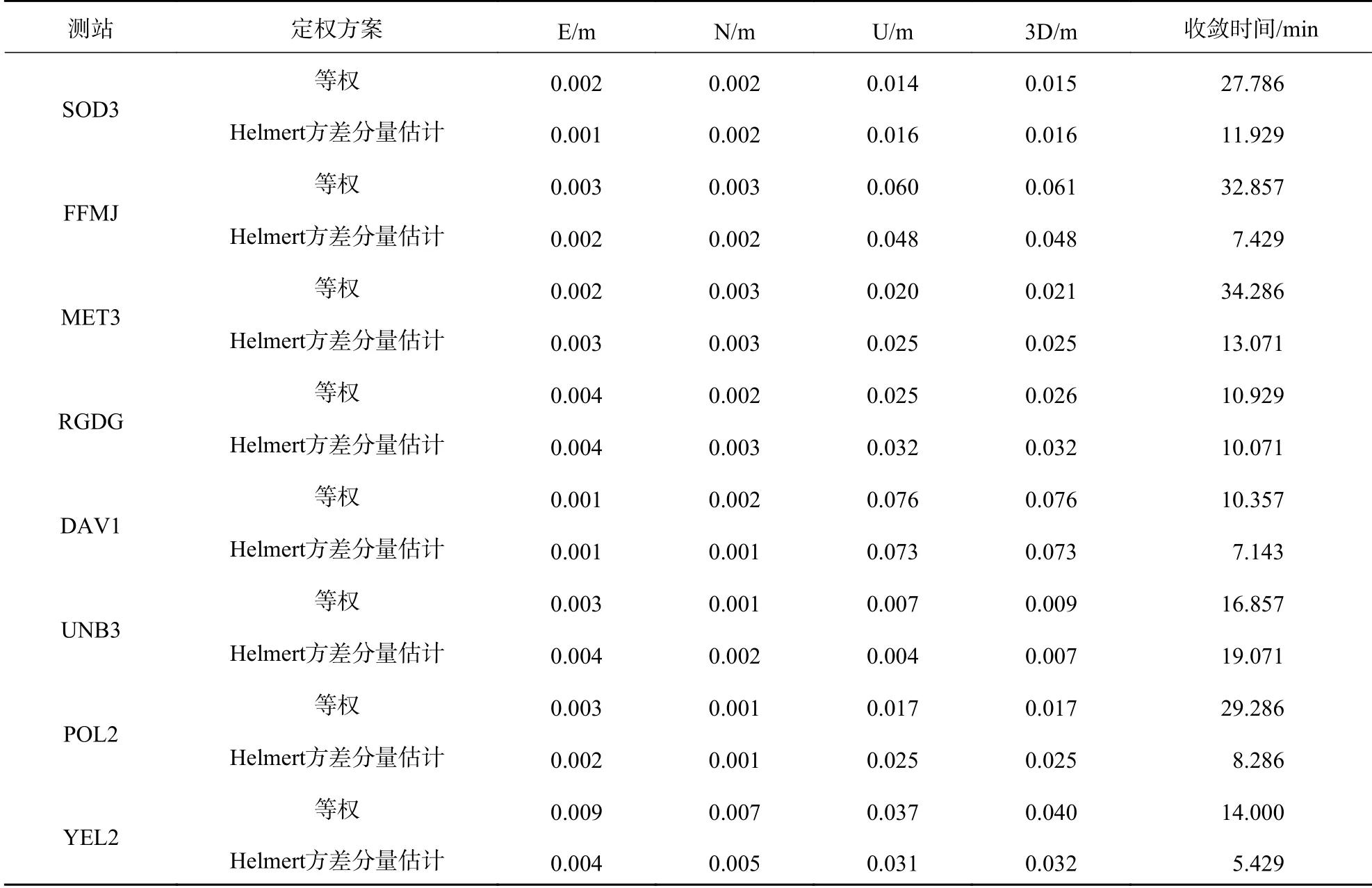
表 2 静态模式下所有站点两种定权方案的定位误差和收敛时间对比

图2～3给出了2021年2月14日DAV1测站Helmert方差分量估计定权方案下GLONASS、BDS、Galileo观测组与GPS观测组之间的权重比及其分布情况. 由于在GPS、GLONASS、BDS和Galileo四系统的Helmert方差分量估计过程中，常数c取，因此，GPS观测组的权重总是1. 以GPS观测组的权重为参考，GLONASS观测组与GPS观测组权重比(GLONASS/GPS)的范围是0.11～9.67. 其中，75%集中分布在0.4～1.4；BDS观测组与GPS观测组权重比(BDS/GPS)的范围为0.02～0.42；Galileo观测组与GPS观测组权重比(Galileo/GPS)的范围为0.10～9.97. 其中，有75%分布在0.6～2.4. GPS、GLONASS、BDS和Galileo观测组的权重的中位数之比为1∶0.9∶0.2∶1.5. 由于该测站BDS系统的数据质量较差(静态模式下和仿动态模式下BDS PPP都超过1 h未能收敛)，所以计算出的BDS系统的权重相对偏小，其GPS和GLONASS相差不大，Galileo的权重相比最大.

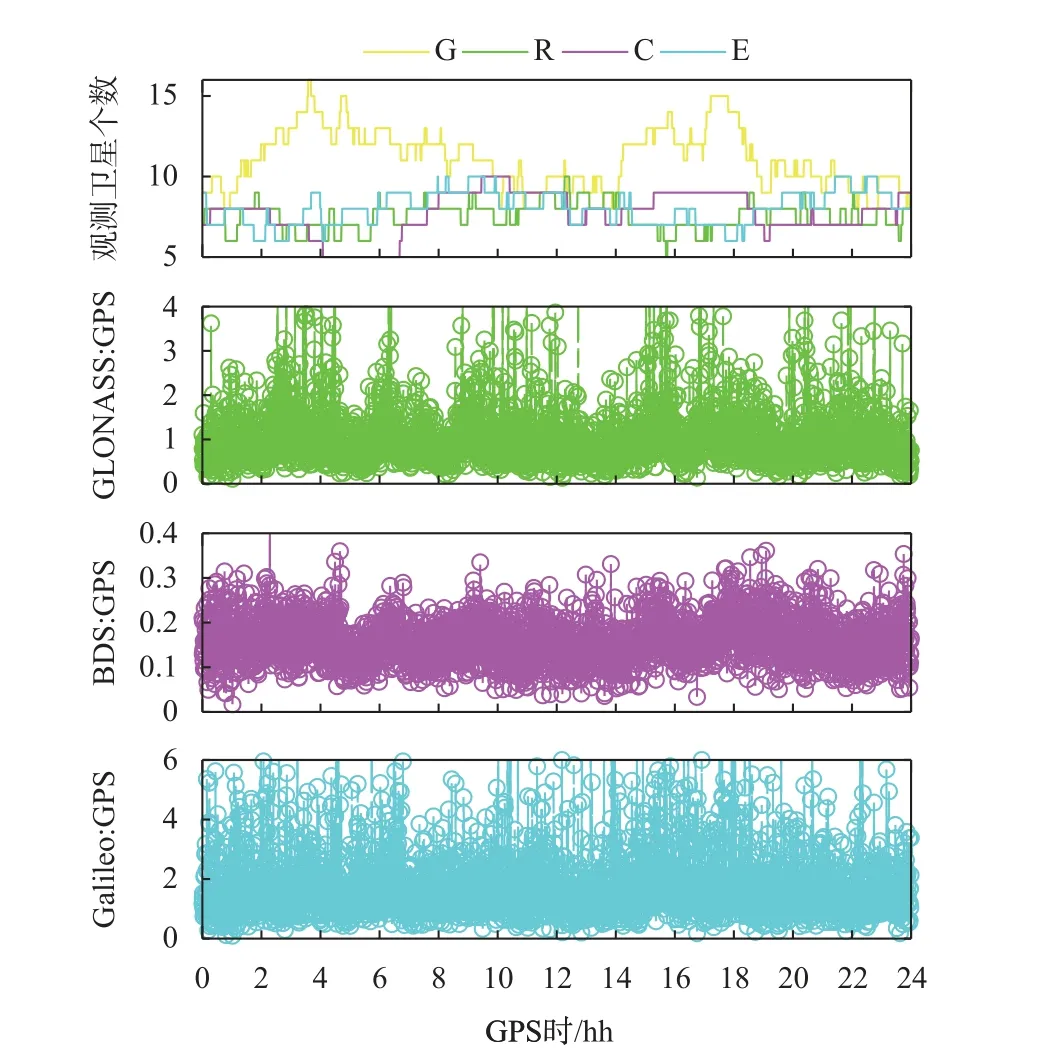
图 2 2021年2月14日DAV1测站不同系统的观测卫星个数及Helmert方差分量估计定权方案下GLONASS、BDS、Galileo观测组与GPS观测组之间的权比

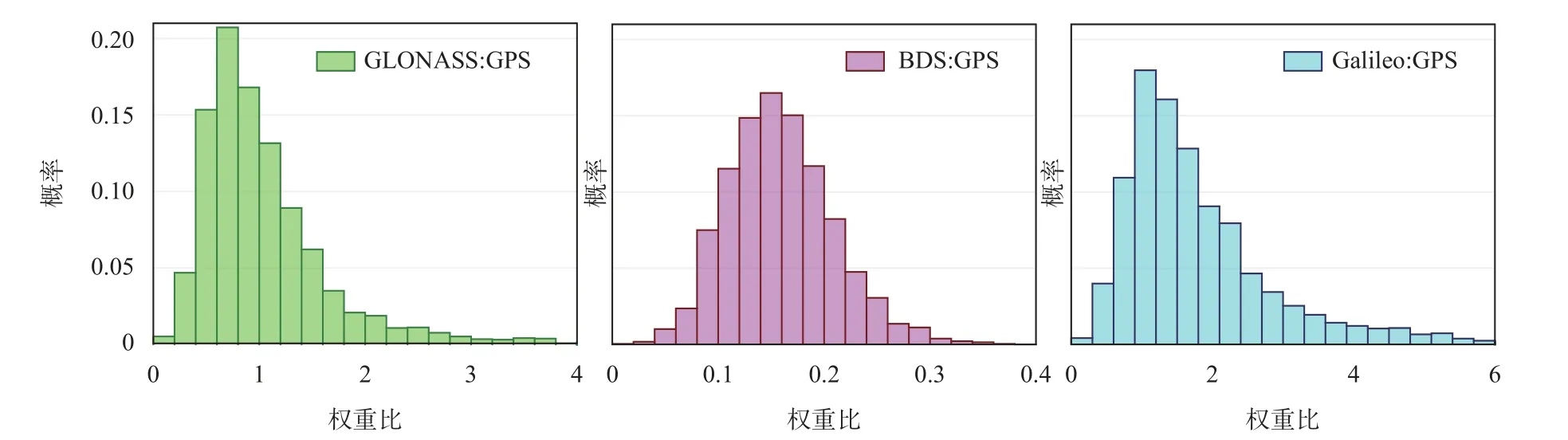
图 3 2021年2月14日DAV1测站Helmert方差分量估计定权方案下GLONASS、BDS、Galileo观测组与GPS观测组之间的权比的分布情况

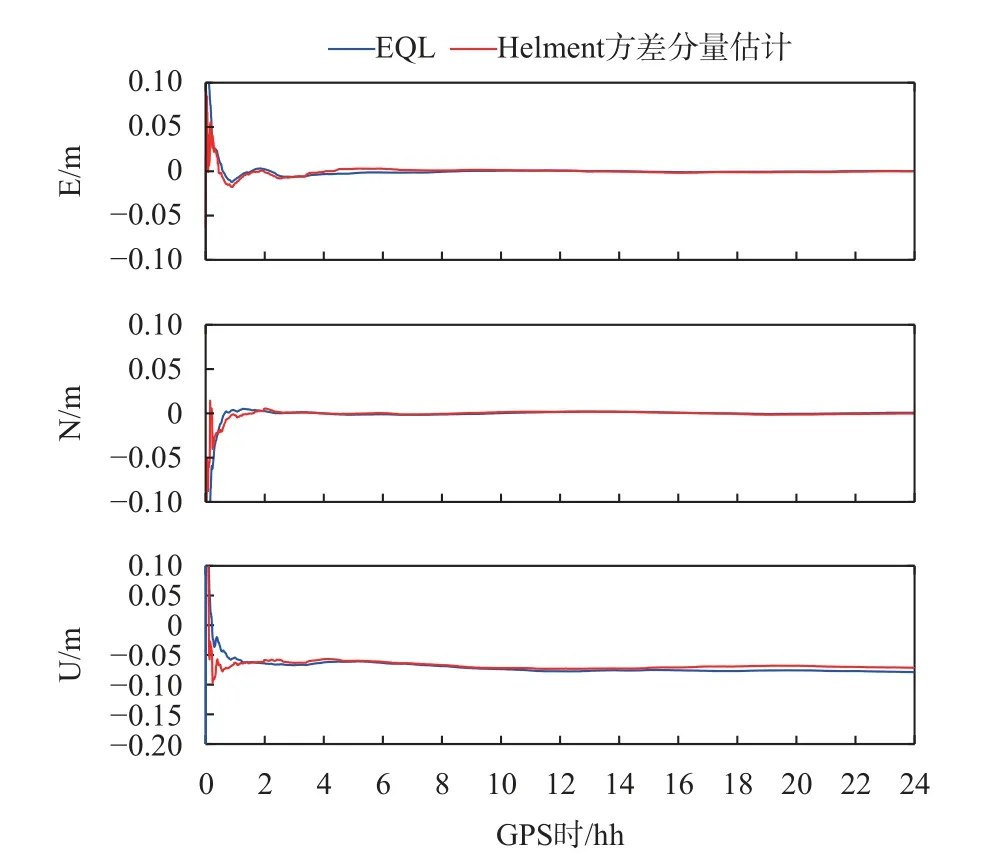
图 4 2021年2月14日静态模式下DAV1测站两种定权方案的E、N、U方向定位误差

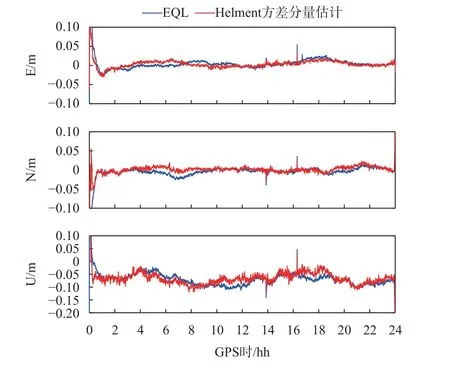
图 5 2021年2月14日仿动态模式下DAV1测站两种定权方案的E、N、U方向定位误差

图4～5给出了2021年2月14日DAV1测站在静态模式下和仿动态模式下使用两种定权方案计算的E、N、U方向定位误差. 由图可知，使用等权定权方案的GPS/GLONASS/BDS/Galileo组合 PPP定位结果在静态和仿动态测试中都差于Helmert方差分量估计方法. 在静态模式下，等权定权方案在E、N、U方向的定位误差分别为0.000 4 m、0.000 8 m、0.079 8 m，3D误差为0.079 8 m，而Helmert方差分量估计定权方案的E、N、U误差和3D误差计算为0.000 3 m、0.000 1 m、0.072 6 m和0.072 6 m. 尽管等权定权方案的定位精度已经达到很高水平，但Helmert方差分量估计定权方案将它的定位性能提高了近10%. 在仿动态模式下，相比于等权定权方案E、N、U方向0.013 7 m、0.013 3 m和0.074 8 m的定位误差， Helmert方差分量估计定权方案分别提高了15%、25%和4%.

图6～7给出了2021年2月14日DAV1测站在静态模式下和仿动态模式下两种定权方案的收敛情况. 两种模式下等权方案的初始化时间为9.5 min和9 min，使用Helmert方差分量估计定权方案分别将初始化时间提高到4 min和4.5 min，收敛速度分别提高了58%和50%. 可以看出，Helmert方差分量估计定权方法的应用对多系统组合PPP的收敛时间有明显的改善效果.

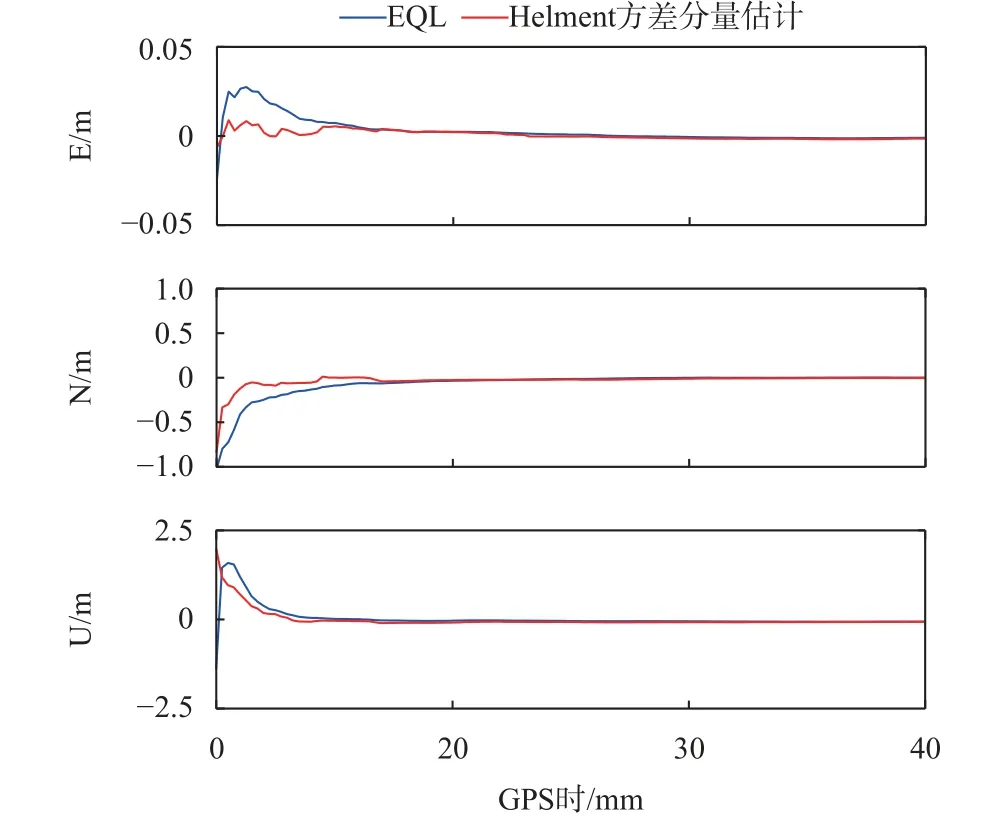
图 6 2021年2月14日静态模式下DAV1测站两种定权方案的收敛情况

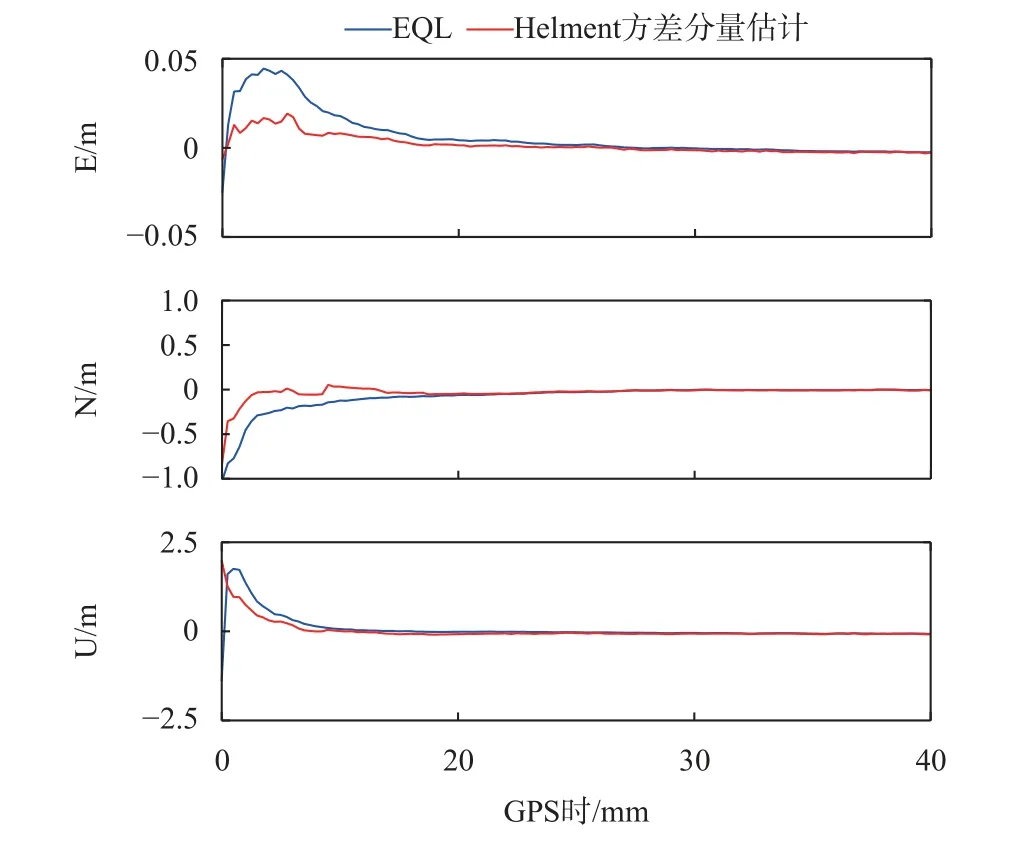
图 7 2021年2月14日仿动态模式下DAV1测站两种定权方案的收敛情况

考虑到10个站点一周内的所有定位过程，表2～3分别给出了静态模式下和仿动态模式下每个站点在E、N、U方向一周结果的平均定位误差、一周结果的平均3D误差和一周结果的平均收敛时间. 静态模式下，等权定权方案和Helmert方差分量估计定权方案的测站平均3D误差分别为0.028 9 m和0.029 0 m，测站平均初始化时间分别为23.2 min和11.1 min. 仿动态模式下，两种方案的测站平均3D误差为0.073 0 m和0.065 7 m，测站平均初始化时间为22 min和8 min. 从图中可以看出，Helmert方差分量估计定权方案的使用在静态和仿动态测试中都能显著提高初始化时间，而定位精度不明显(静态测试几乎一样，仿动态测试有10%的改善). 在静态和仿动态测试中，使用Helmert方差分量估计定权方案，收敛速度分别提高了52%和64%，其中，FFMJ测站的改善率静态可以达到77%，仿动态可以达到88%.

表 2（续）

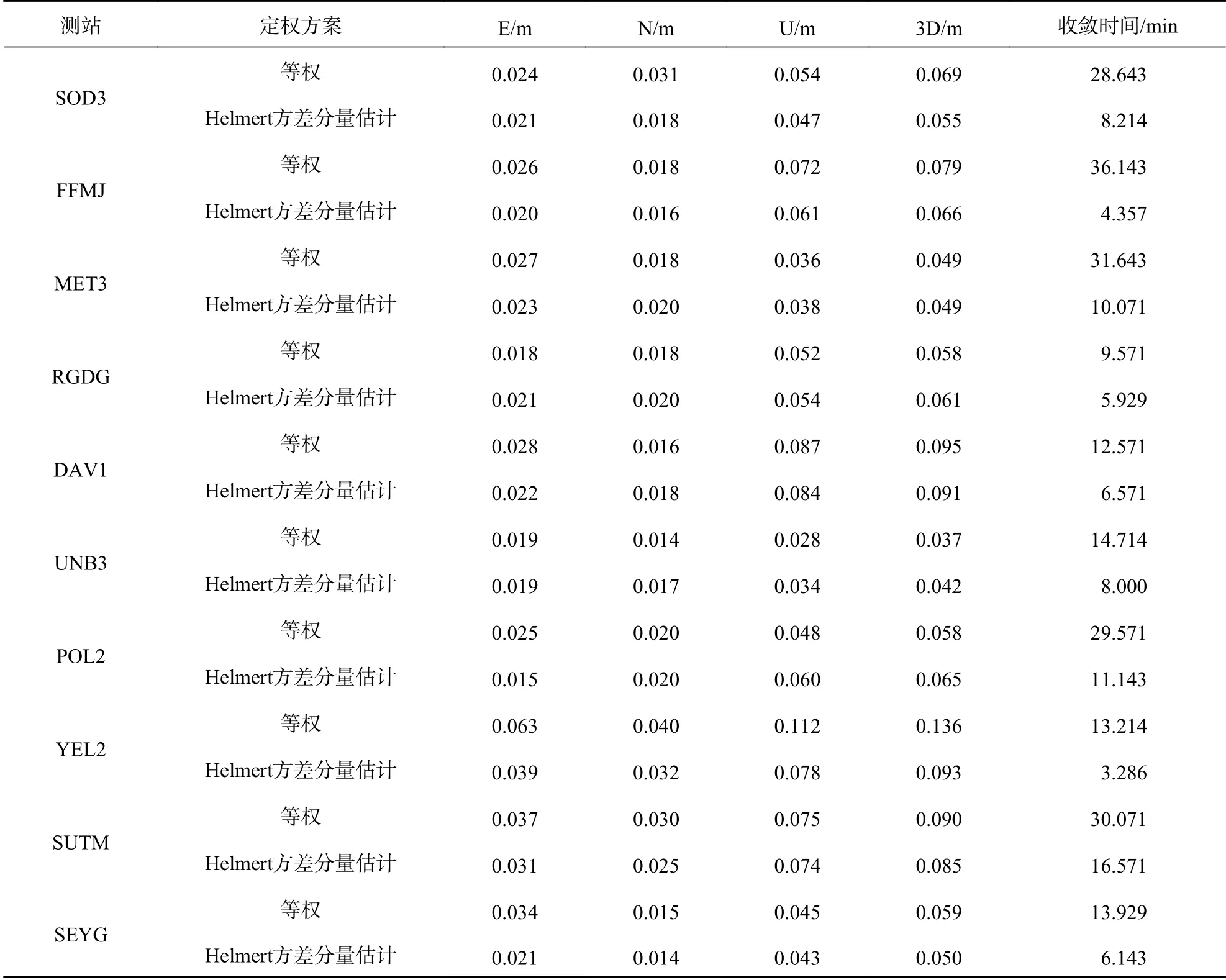
表 3 静态仿动态模式下所有站点两种定权方案的定位误差和收敛时间对比

4 结 论

由于多模GNSS系统间信号结构、频率、信噪比和信号传输路径的差异，采用等价权比进行组合定位难以得到最优的结果. 基于此，本文在给出 GPS/GLONASS/BDS/Galileo 组合PPP的函数模型、随机模型和参数估计方法基础上，使用Helmert方差分量估计方法确定GPS、GLONASS、BDS和Galileo观测组的权比，最后采用全球IGS MGEX观测网的10个测站一周的观测数据进行静态和仿动态试验，以分析验证本文方法的可行性和有效性. 试验结果表明：在GPS/GLONASS/BDS/Galileo 组合 PPP定位中，Helmert方差分量估计定权方法优于传统定权方法，可动态准确确定GPS、GLONASS、BDS和Galileo观测组之间的权比，并显著提高了组合 PPP的收敛速度，静态模式下平均提高52%，仿动态模式下平均提高64%，但定位精度未有明显改善，主要原因是PPP的定位精度主要由载波相位观测值精度和误差修正水平决定，因此改变系统间权比对多星座组合PPP的定位精度改善不显著.