超越模型在比较大小问题中的应用

丁 涛

(青岛市黄岛区博文中学)

以函数为背景的比较大小问题,是近年高考的常考题型,多以选择题的形式出现,且常出现在压轴题的位置,学生因不清楚这类题目的命题原理,因此在高考有限的时间内,往往不能快速、准确地解答问题.通过深入研究,笔者发现此类问题大多以某一函数为背景,以函数的性质为切入点.因此在求解问题时只要准确构造相应的函数型,即可顺利解答.笔者发现常用的函数模型有以及这两个函数的倒数函数.下面就针对这几个函数模型的应用进行举例说明.

例1下列不等关系中不正确的是( ).

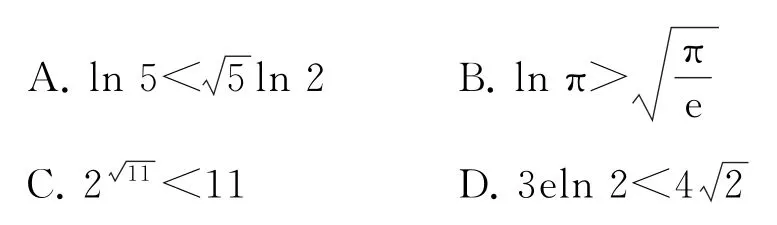
综上,故选A.

例2已知,其中e为自然对数的底数,则a,b,c的大小关系为( ).

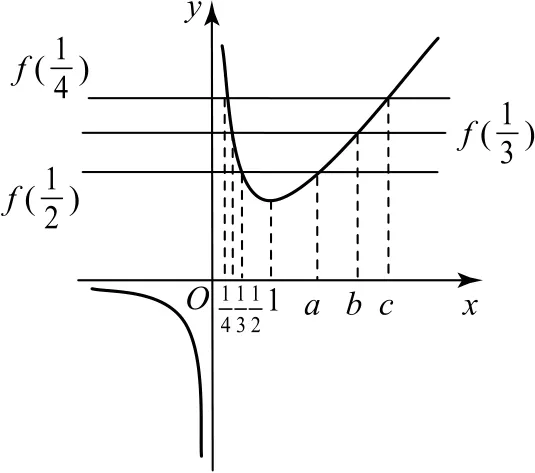
图1

例3设,则a,b,c的大小关系为( ).

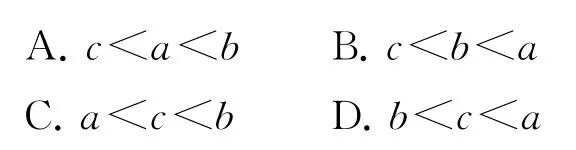
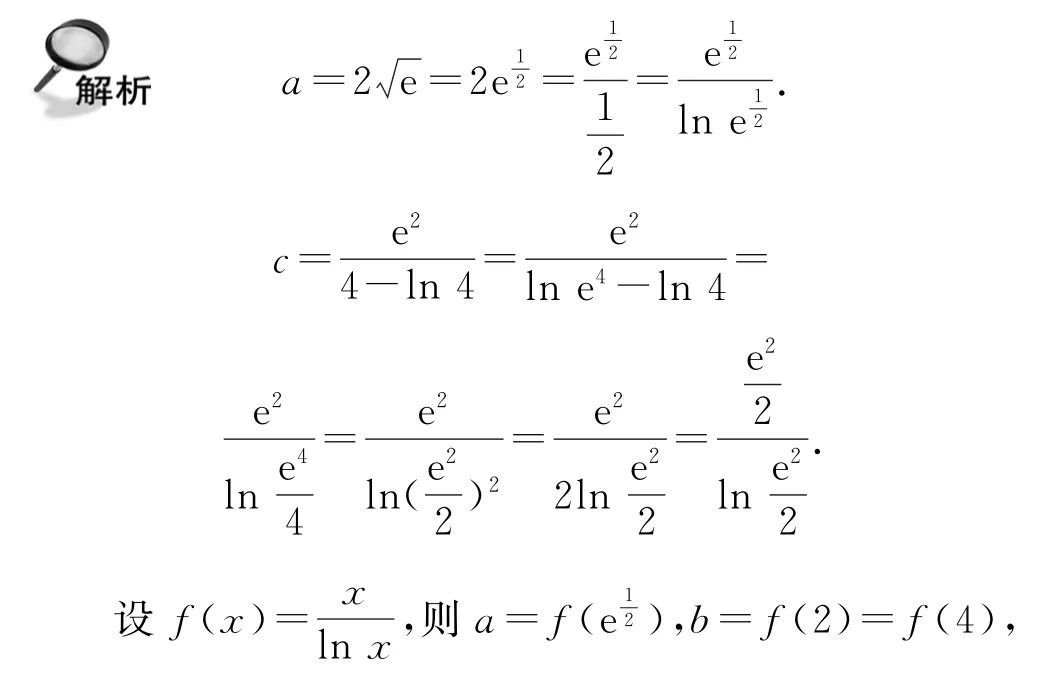
综上,c＜b＜a,故选B.

例4已知实数a,b,c满足b＞1,则a,b,c的大小关系为( ).

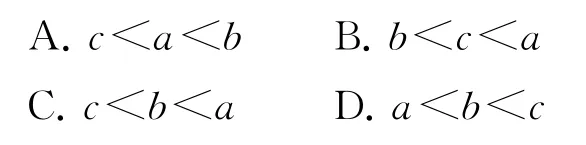
已知b＞1,即lna＞0,c＜0,所以a＞1.

设函数g(x)＝lnx－x(x＞0),求导得g′(x)＝,所以函数g(x)在区间(0,1)内单调递增,在区间(1,＋∞)内单调递减,gmax(x)＝g(1)＝ln1－1＝－1＜0,所以lnx＜x(x＞0),所以lna＜a,即

综上,b＞a＞c,故选A.

处理比较大小问题,除了构造几种超越函数模型外,还要熟悉基本指数函数、对数函数、幂函数的图像和性质,以及不同函数之间的位置关系.

(完)