强基计划数学备考系列讲座(7)——集合与函数(下)

王雪芹 王慧兴

(1.北京师范大学第二附属中学 2.清华大学附属中学)

3.9 方程与不等式

强基校考命题注重考查函数观点支撑下的解不等式及其应用.

例14(清华大学)定义在R 上的函数f:R→R满足:f(x3)＝[f(x)]3(∀x∈R),f(x1)≠f(x2)(∀x1≠x2),则f(0)＋f(－1)＋f(1)的 值是_________.

解析由题设得f(－1)＝[f(－1)]3,f(0)＝[f(0)]3,f(1)＝[f(1)]3,所以f(0),f(－1),f(1)是方程x3－x＝0的三个根,故

例 15(复旦大学)已 知g(x)＝,解不等式0＜g(f(x))＜1.

解析按题意,不等式的解集W⊆(0,＋∞),所以先作划分:

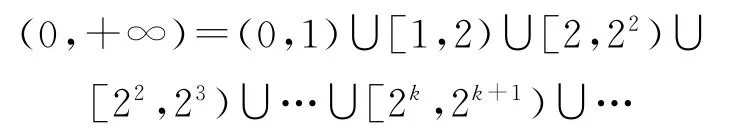
当x∈(0,1)时,f(x)＝log2x＜0,所以[f(x)＋|f(x)|－2]＝－2,且f(x)＋[f(x)]＜0,从而

所以只需f(x)＋[f(x)]＋4＞0,因为h(t)＝t＋[t]＋4(t＝f(x)＜0)不减,而且当时,t＝,则h(－2)＝0,所以满足g(f(x))＞0的x取值范围是

任取x∈[2k,2k＋1)(k∈N),则f(x)∈[k,k＋1),[f(x)]＝k,2f(x)－2∈[2k－2,2k),故

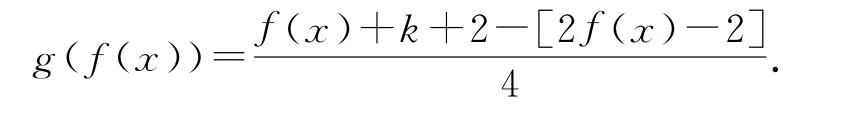
当2f(x)－2∈[2k－2,2k－1)时,有[2f(x)－2]＝2k－2,所以所以满足2f(x)－2＜2k－1的x∈[2k,2k＋1)(k∈N)都不满足题意.

3.10 复合与迭代

函数复合与迭代运算蕴含递推等丰富的数学方法,抓住复杂函数关系中的迭代结构,能够化繁为简,出奇制胜.

例16解方程

解析把原方程化为

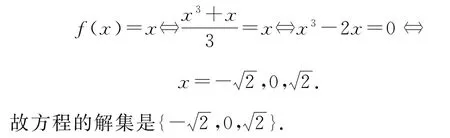
例17(复旦大学)已知函数f(x)＝x2－1,则函数y＝f(f(x))的图像大致为_________(填图).

解析由迭代运算y＝f(f(x))＝[f(x)]2－1.如图4所示,先由函数f(x)＝x2－1的图像,作出函数y＝|f(x)|的图像,再作出函数y＝[f(x)]2－1的图像,经向下平移1个单位即得函数y＝[f(x)]2－1 的图像,此即复合函数y＝f(f(x))的图像.

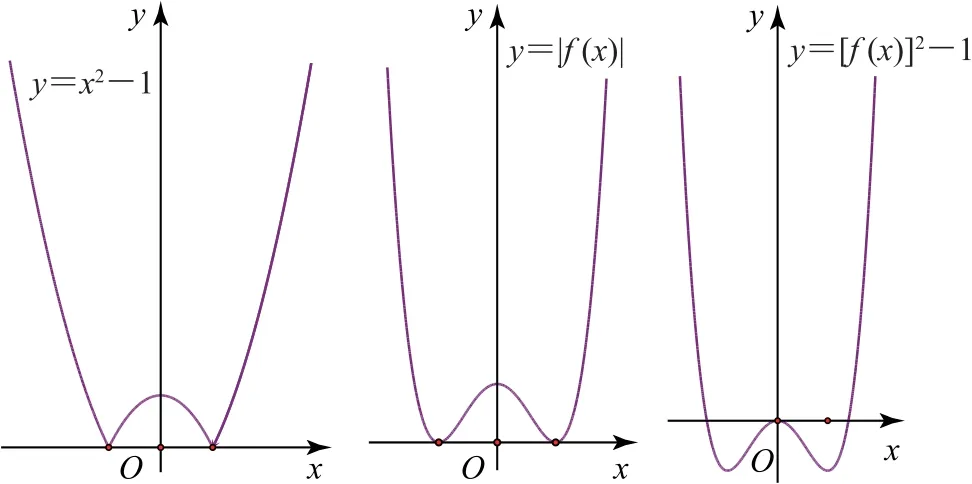
图4

3.11 最值探究

最值探究包含探求单变量函数最值、多元函数最值以及复合最值,当然,导数是最值探究的重要工具,但我们这里主观上限制不用导数,注重变形路径.

例19对一切x∈[a,b],|x2－kx－m|≤1成立,求δ＝b－a的最大值.

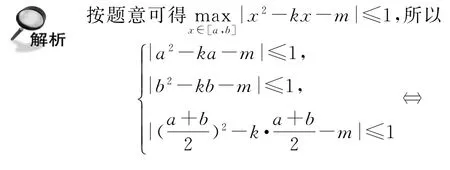
解析探究含参数恒成立问题中的参数条件以及带参数最值都是高校特招试题立意的亮点.

例20(北京大学)对一切x,y＞0,都有5x＋,求实数a的最小值.

对题设不等式调结构——分离参数,得a≥∀x,y＞0.

点评本题基于换元和减元,把多元情境转换为单变量情境,进而应用一元函数求解多元最值.但利用均值不等式求最值,计算过程要简捷一些.由,得5x＋,等号成立的条件是,故fmax＝9.

例21(上海交大)函数f(x)＝|x2－a|在闭区间[－1,1]上的最大值记作m(a),则m(a)的最小值是_________.

点评本例属“含参函数复合最值”,另一类形如例22,属于“多函数复合最值”.

例22(北京大学)求函数f(x)＝max{1－x,

解析,x2}(x∈R)的最小值.

任取x∈R,比较三个数,x2的大小,取其最大的与x相对应,由此建立一个定义在R上的函数,进而利用数形结合思想求其最小值可以分段或画图处理,当然也可合理减元、适度放缩求解.

一方面,因为

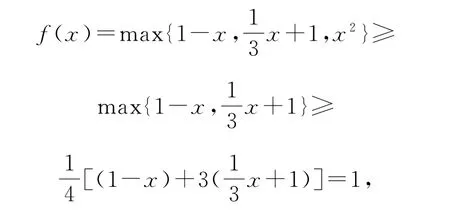
所以fmin(x)≥1.

另一方面,由f(0)＝max{1,1,0}＝1,可得fmin(x)≤1.

综上,fmin(x)＝1.

3.12 抽象函数

抽象函数情境能够有效培育学生数学抽象素养,提升数学理解与综合分析能力,同时历练抽象函数问题能为深入分析、求解函数方程做好铺垫.

例23(北京大学)定义在(－1,1)上的函数f(x)满足两个条件:①f(x)＞0,∀x∈(－1,0);②,x,y∈(－1,1).则f(x)为( ).

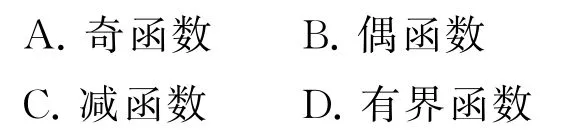
解析∀x∈(－1,1),取y＝－x,代入②得

在②中,取x＝y＝0,得f(0)＝0,代入③,得f(－x)＝－f(x),∀x∈(－1,1),故f(x)是奇函数,选项A 正确,结合条件①可知选项B不正确.

∀x∈(0,1),有－x∈(－1,0),所以

任取－1＜x1＜x2＜1,代入条件②,得

即f(x2)＜f(x1),故f(x)是减函数,选项C正确,B不正确.

综上,选AC.

3.13 函数方程

在强基计划数学测试中,立意柯西方程及其变式的函数方程问题比较常见.

例24求所有函数f:Z→Z,使得∀a,b∈Z,都有f(2a)＋2f(b)＝f(f(a＋b)).

解析f(x)＝0是平凡解,以下设f(x)不为常数.因为

令F(x)＝f(x)－f(0),则式③可以转化为如下柯西方程:

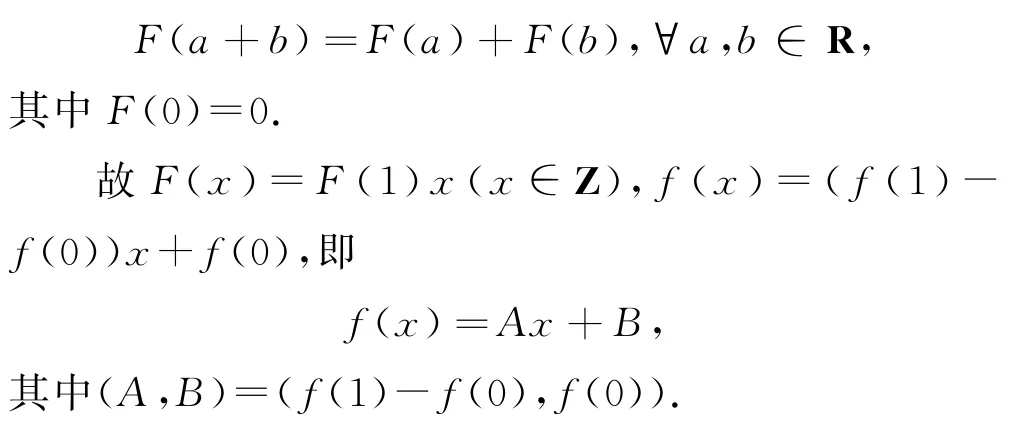
代入题设函数方程得

综上,f(x)＝0(x∈Z)或f(x)＝2x＋B(x∈Z),其中B是任一整数.

例25(清华大学)给定a∈R,函数f:R→R 满足,f(x＋y)＝f(x)f(a－y)＋f(y)f(a－x)(∀x,y∈R),则( ).

解析在题设函数方程中,取x＝y＝0,由f(0)＝,得f(0)＝f(0)f(a)＋f(0)f(a)＝f(a),所以选项A 正确.

在题设函数方程中,取y＝0,∀x∈R,得

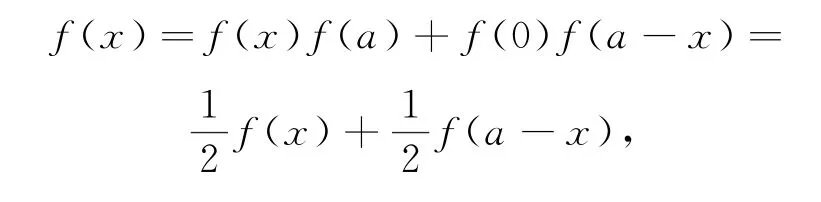
所以f(a－x)＝f(x)(∀x∈R),则题设函数方程为

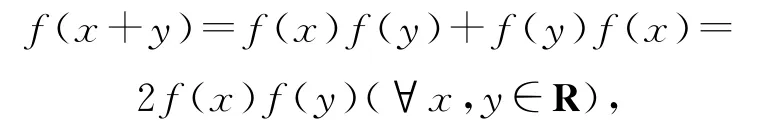
故选项C正确.

任取x∈R,以分别替换题设函数方程中的x,y,得

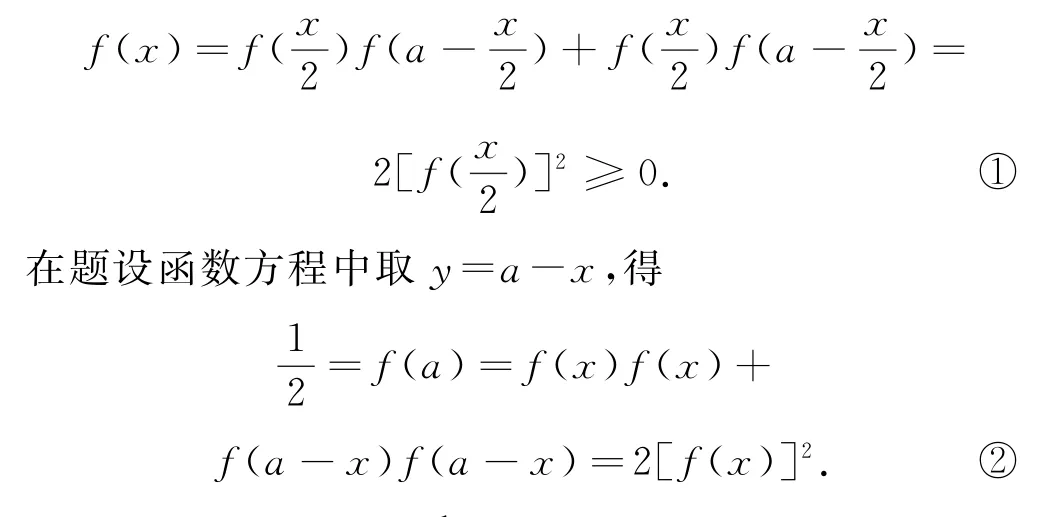
综上,故选ABC.

点评由已得等式f(x＋y)＝2f(x)f(y)(∀x,y∈R),得,则,从而(∀x∈R).进而可以化为柯西方程

令ln(2f(x))＝g(x)(x∈R),得g:R→R 满足柯西方程g(x＋y)＝g(x)＋g(y)(x,y∈R),由柯西方程得其连续解g(x)＝kx,所以,其中常数c＝g(1)＝ln(2f(1)).

但已得到的性质f(a－x)＝f(x)(∀x∈R),表明函数f:R→R的图像关于直线对称,所以必有c＝1,即

遗憾的是命题者可能是受学生常态知识所限,没有给出连续性条件,这样应用柯西方程就不够严谨.

例26(中国科学技术大学)求所有函数f:R→R,使得对一切x,y∈R都有

解析按题意,有f(0)＝f(f(x)－f(x))＝f(f(x))＋2f(x)f(x)＋f(f(x))－1＝2f(f(x))＋2[f(x)]2－1,所以

再由①和②,可得∀x,y∈R,都有

再由①,可得f(x－f(y))－f(x)＋1＝2xf(y)＋f(f(y)),所以∀x,y∈R,都有

故∀x∈R,都存在u,v∈R,使得x＝f(u)－f(v)＋1,故对一切u,v∈R,有

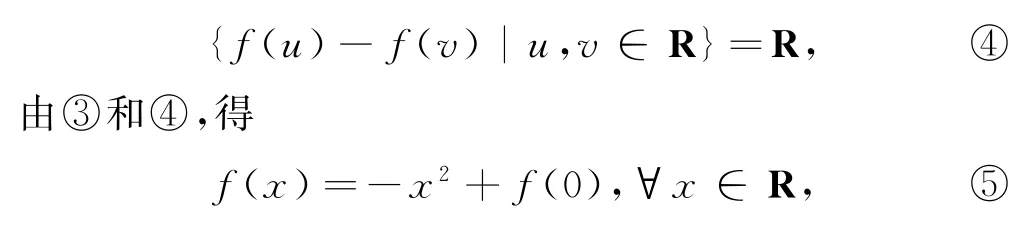
代回式①,得∀x,y∈R,都有

所以,满足题设条件的函数f:R→R为f(x)＝1－x2(x∈R).

点评本例体现求解函数方程的基本方法——替换、减元、对称、同构、任意性、必要性与充分性.

3.14 综合应用

强基校考重视函数应用,应用型函数问题多种多样,多以处理带参数不等关系问题表现函数应用.

例27(中国科学技术大学)若函数f(x)＝(x－1)2＋k2,并且∀a,b,c∈(0,1),都存在以f(a),f(b),f(c)为边的三角形,求k的范围.

解析把定义域拓展到[0,1],按题意,其等价条件是2k2＝2f(1)＝2fmin(x)≥fmax(x)＝f(0)＝1＋k2⇔k2≥1⇔k≤－1或k≥1,故实数k的取值范围是(－∞,－1]∪[1,＋∞).

例28(复旦大学)给定5个函数,其中3个奇函数,2个偶函数,则在这5个函数中任意取3个,其中既有奇函数又有偶函数的概率是.

4 实战演练

1.(上海交通大学)若集合M中任意两个元素的和、差、积、商(分母不为零)都还在M内,则称集合M是封闭的.在集合R,Q,∁RQ,n∈Z中,封闭的集合个数是_________.

2.(上海交通大学)已知集合M＝{(x,y)|x(x－1)≤y(1－y)},N＝{(x,y)|x2＋y2≤k}满足M⊂N,则实数k的最小值是_________.

3.(浙江大学)设M＝{x∈R|f(x)＝x},N＝{x∈R|f(f(x))＝x}.

(1)求证:M⊆N;

(2)当f:R→R 是增函数,是否有M＝N? 证明你的结论.

4.(上海交通大学)已知二次函数f(x)＝ax2＋bx＋c(a≠0)没有不动点,则它是否有稳定点? 证明你的结论.

5.(上海交通大学)证明:若f(f(x))有唯一不动点,则f(x)也有唯一不动点.

6.(上海交通大学)求集合A＝{a1,a2,…,an}⊂N*(n≥2),满足a1＋a2＋…＋an＝a1·a2·…·an.

7.(复旦大学)命题p:“△ABC的内心与外心重合”是命题q:“△ABC是正三角形”的什么条件?

8.(清华大学)《红楼梦》《三国演义》《水浒传》和《西游记》四部书陈列在四层架子书柜的不同层上,小赵、小钱、小孙、小李分别借阅了四部书中的一部.现已知:小钱借阅了第一层的书籍,小赵借阅了第二层的书籍,小孙借阅的是《红楼梦》,《三国演义》在第四层,则( ).

A.《水浒传》一定陈列在第二层

B.《西游记》一定陈列在第一层

C.小孙借阅的一定是第三层上的书籍

D.小李借阅的一定是第四层上的书籍

9.(上海交通大学)设常数c∈(0,1),函数f(x)的定义域为(0,1),则函数g(x)＝f(x＋c)＋f(xc)的定义域为________.

10.(清华大学)给定三次函数p(x)＝x3－3x＋1.

(1)证明:函数p(x)有三个零点a＜b＜c;

(2)证明:若x＝t是p(x)的一个零点,则x＝t2－2也是p(x)的一个零点;

(3)定义映射f:{a,b,c}→{a,b,c},x|→x2－2,求f(a),f(b),f(c).

11.设x,y∈R.

(1)若x,y∈(－2,1),求证:2(x2＋xy＋y2)＋3xy＜12;

(2)求证:x2＋xy＋y2＋3(x＋y)＋6＞0;

(3)求证:x2＋xy＋y2－3(x＋y)＋3≥0.

12.(南京大学)已知0≤a＋b,b＋c,c＋a≤1,求的最值.

13.(中国科学技术大学)已知a＞0,二次函数f(x)＝ax2－x＋1,若在任意长度为1的区间上,存在两点函数值之差不小于1,则a的最小值为_________.

15.(上海交通大学)已知方程2x－sinx＝1,则下列判断:

①方程没有正数解;

②方程有无穷多个解;

③方程有一个正数解;

④方程的实根小于1.

其中错误的判断有________.

A.f(x,y,z)既有最大值也有最小值

B.f(x,y,z)有最大值但无最小值

C.f(x,y,z)有最小值但无最大值

D.前三个答案都不对

A.1 B.2 C.3 D.前三个答案都不对

18.(中国科学技术大学)求所有a∈R,使得f(x)＝x3＋ax2－x＋1－a,满足|f(x)|≥|x|,∀x∈[－1,1].

19.(南京大学)求函数f:R→R,使得f(f(x＋y))＝f(x＋y)＋f(x)f(y)－xy(∀x,y∈R).

20.设实数a,b,c＞0,若一元二次方程ax2＋bx＋c＝0有实根,则( ).

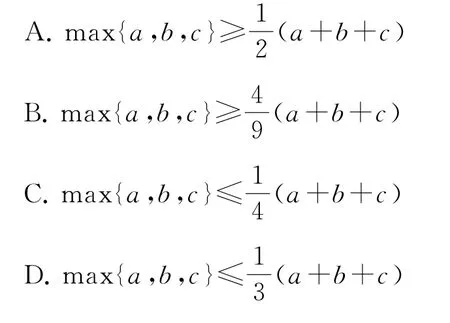
(完)