四基为本与时俱进，素养为魂稳中求进——全国新高考Ⅰ卷数学试题评析

陈选明

(江西师范大学附属中学)

2022年全国新高考Ⅰ卷数学试题,体现高考内容改革的总体要求,符合《普通高中数学课程标准(2017年版2020年修订)》理念,聚焦数学学科六大核心素养,突出关键能力的考查,体现了高考数学的选拔功能和育人导向.试题突出数学本质,重视以理性思维能力为主的命题原则,发挥选拔人才的功能,绝对摒弃刷题就能得高分的理念,从而引导中学教学要遵循教学规律,提高课堂的时效性,让学生成为课堂的主人,杜绝学生“死读书”和教师“教死书”的陈旧教学模式,培养创新性人才是中学教学的真正目标.

1 注重基础知识，考查数学本质

试题重视考查数学的基础知识和基本方法,重点考查主干知识与核心概念,更加突出考查数学的学科本质,注重考查本源性方法.试题不是通过新情境、新背景、陌生的数学文化等来增加难度,而是单纯地通过对数学主干知识的考查,让学生对基本定义、基本方法、基本运算达到灵活应用的水平,也是数学学科素养要求学生必须要具备的基本能力.

和以往不同的是第20题概率统计试题第(2)问考查了条件概率的证明,学生必须非常熟悉条件概率公式才能顺利证明.这一方面考查了学生的推理论证能力,另一方面也体现出要加强对概念的教学,重视知识的生成过程.

2022年新高考Ⅰ卷第20题在考查独立性检验的基础上,又侧重于条件概率的推导,是一道理论联系实际、让学生认识到概率统计的广泛应用的好题,难度不大,不以计算作为唯一考点,客观上服务了“双减”政策实施,而且题目立意新颖,具有创新性,突出了关键能力和“数学运算、逻辑推理”核心素养,对一线教师的教学有导向功能,也能够有效区分,不为题海战术开方便之门.这类题目以后在高考中会越来越多,因为这种新题可以反套路,反题海战术.

例1(2022 年新高考Ⅰ卷16)已知椭圆C:,C的上顶点为A,两个焦点为F1,F2,离心率为.过F1且垂直于AF2的直线与C交于D,E两点,|DE|＝6,则△ADE的周长是_________.

解析方法1(定义法)因为椭圆的离心率为e＝,所以a＝2c,则b2＝a2－c2＝3c2,故椭圆的方程为,即3x2＋4y2－12c2＝0,不妨设左焦点为F1,右焦点为F2.

如图1所示,因为|AF2|＝a,|OF2|＝c,a＝2c,所 以∠AF2O＝,所以△AF1F2为正三角形,因为过F1且垂直于AF2的直线与C交于D,E两点,所以DE为线段AF2的垂直平分线,所以直线DE的斜率为,则直线DE的方程为,代入椭圆方程3x2＋4y2－12c2＝0,得,则

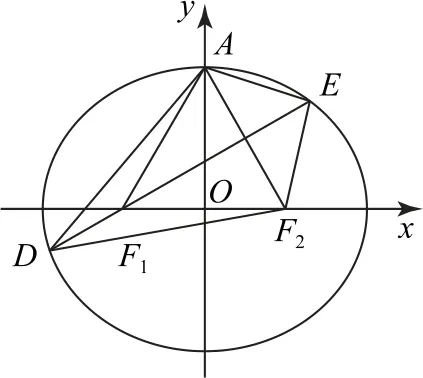
图1

因为DE为线段AF2的垂直平分线,根据对称性可得AD＝DF2,AE＝EF2,所以△ADE的周长等于△F2DE的周长,利用椭圆的定义得△F2DE周长为

故△ADE的周长为13.

方法2(利用焦半径公式)因为△AF1F2为等边三角形,DE为线段EF1的中垂线,所以EA＝EF2,DA＝DF2,△ADE的周长等于△DF2E的周长,即4a,因为

2 创新问题情境，坚持素养导向

素养导向下的命题在试题的情境和设问上,适度变化,强调数学素养的发展,试题关注数学知识和方法的灵活应用.实际问题情境关注学生的身边事,体现了数学源于生活且高于生活,以及数学作为基础学科的应用价值.

2.1 数学文化与数学应用齐飞

试题背景素材紧密联系国家社会经济发展、生产生活实际.如第4题以我国的重大建设成就“南水北调”工程为素材考查台体的体积计算,但并没有直接考查,而是将此知识融入实际生活情境中,考查学生的空间想象能力、数学阅读理解能力、运算求解能力,对数学抽象、数学建模等数学核心素养也提出了相应的要求,引导学生关注社会主义建设的伟大成果,增强社会责任感.第20题以地方疾病与卫生习惯为背景,让考生体验从特殊到一般的数学问题探索过程,重点考查学生灵活运用数学知识分析问题的能力.

例2(2022年新高考Ⅰ卷4)南水北调工程缓解了北方一些地区水资源短缺问题,其中一部分水蓄入某水库.已知该水库水位为海拔148.5 m 时,相应水面的面积为140.0km2;水位为海拔157.5 m 时,相应水面的面积为180.0km2,将该水库在这两个水位间的形状看作一个棱台,则该水库水位从海拔148.5m上升到157.5 m 时,增加的水量约为2.65)( ).

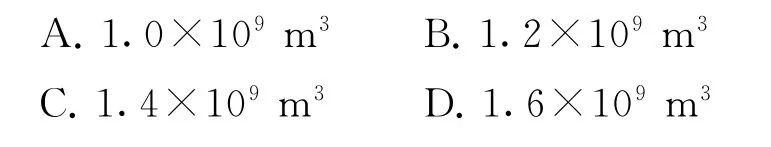
解析依题意可知棱台的高为h＝157.5－148.5＝9m.棱台上底面积为S＝140.0km2＝1.4×108m2,下底面积为S′＝180.0km2＝1.8×108m2,所以

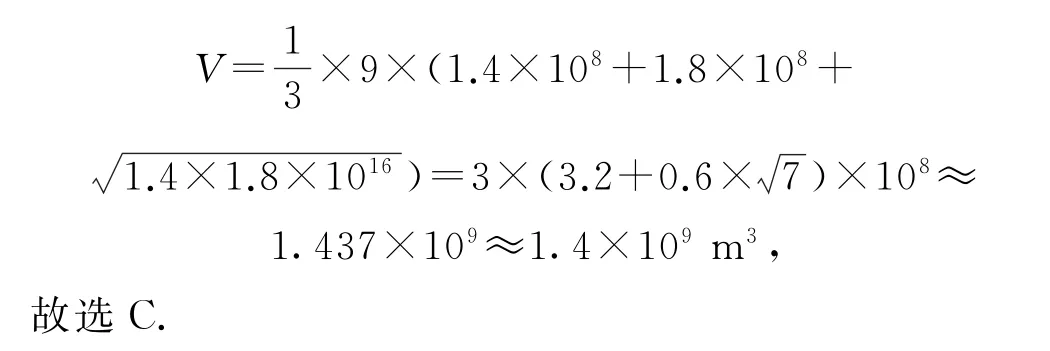
2.2 数学思想与核心素养并举

为了实现对学生素养的考查,高考命题加强对数学思想方法的考查,今年的新高考Ⅰ卷体现得较为充分.蕴含数形结合思想的试题:第3,6,11,12,14,15,16,21,22题;蕴含转化与化归思想的试题:第10,17,18题;考查直观想象素养的试题:第4,8,9,19题;考查数学运算素养的试题:第1,2,5,7,13,17,18,20题;考查逻辑推理素养的试题:第8,12,22题.命题从知识立意到能力立意,再到学科素养立意,都是以数学知识为载体,考查学生理性思维的广度与深度,体现了“双基”、数学思想的重要性.

例3(2022年新高考Ⅰ卷8)已知正四棱锥的侧棱长为l,其各顶点都在同一球面上.若该球的体积为36π,且则该正四棱锥体积的取值范围是( ).

解析方法1因为球的体积为36π,所以球的半径R＝3,设正四棱锥的底面边长为2a,高为h,则l2＝2a2＋h2,32＝2a2＋(h－3)2,所以6h＝l2,2a2＝l2－h2,所以正四棱锥的体积为

方法2设正四棱锥的高与侧棱夹角为θ,高为h,底面中心到各顶点的距离为m,则

3 突出理性思维，彰显选拔功能

高考试题强调对能力的考查,今年的试题更加强化对数学运算、推理论证以及抽象概括能力的考查,整份试题对学生数学运算能力要求较高.

例4(2022年新高考Ⅰ卷7)设a＝0.1e0.1,b＝,c＝－ln0.9,则( ).

解析方法1(利用放缩工具快速求解)

放缩工具:

2)ex≥x＋1,当且仅当x＝0时等号成立;

由1)可知

综上,c＜a＜b,故选C.

方法2(利用放缩工具+构造函数)

放缩工具:

综上,c＜a＜b,故选C.

方法3(同构法)

要比较a,b的大小,根据作商比较法只需比较(1－0.1)e0.1与1的大小,构造函数h(x)＝(1－x)ex(0≤x≤1),则h′(x)＝－xex,易知h(x)在[0,1)上单调递减,所以h(0.1)＜h(0)＝1,即a＜b.

要比较a,c的大小,同方法2可知c＜a.

综上,c＜a＜b,故选C.

4 加强教考衔接，发挥引导作用

“立意新颖,不为题海战术开方便之门;界定明确,对一线教师的教学有导向功能;有效区分,让不同水平的学生高低立显.”这是对2022全国新高考Ⅰ卷数学的总体感知.旨在引导我们认识到,教师的“教”要遵循教学规律,学生的“学”更多的是要将知识和方法内化成自身的知识结构,低效的学习方式只会徒增师生的压力和负担.知识的获取与素养的形成都要遵循基本规律,才能创新,打牢知识功底.

例5(2022年新高考Ⅰ卷22)已知函数f(x)＝ex－ax和g(x)＝ax－lnx有相同的最小值.

(1)求a;

(2)证明:存在直线y＝b,其与两条曲线y＝f(x)和y＝g(x)共有三个不同的交点,并且从左到右的三个交点的横坐标成等差数列.

解析(1)a＝1(求解过程略).

(2)方法1由(1)可得f(x)＝ex－x和g(x)＝x－lnx的最小值均为1.

当b＞1时,分别考虑ex－x＝b和x－lnx＝b的解的个数.

设S(x)＝ex－x－b,S′(x)＝ex－1,当x＜0时,S′(x)＜0,当x＞0 时,S′(x)＞0,故S(x)在(－∞,0)上为减函数,在(0,＋∞)上为增函数,所以Smin(x)＝S(0)＝1－b＜0.而S(－b)＝e－b＞0,S(b)＝eb－2b,设u(b)＝eb－2b,其中b＞1,则u′(b)＝eb－2＞0,故u(b)在(1,＋∞)上为增函数,所以u(b)＞u(1)＝e－2＞0,故S(b)＞0,所以S(x)＝ex－x－b有两个不同的零点,即ex－x＝b的解的个数为2.

设T(x)＝x－lnx－b,则

当0＜x＜1时,T′(x)＜0,当x＞1时,T′(x)＞0,故T(x)在(0,1)上为减函数,在(1,＋∞)上为增函数,所以Tmin(x)＝T(1)＝1－b＜0.而T(e－b)＝e－b＞0,T(eb)＝eb－2b＞0,T(x)＝x－lnx－b有两个不同的零点,即x－lnx＝b的解的个数为2.

当b＝1,由(1)可得x－lnx＝b,ex－x＝b均有一个零点.

当b＜1时,由(1)可得x－lnx＝b,ex－x＝b均无零点,故若存在直线y＝b与曲线y＝f(x),y＝g(x)有三个不同的交点,则b＞1.

设h(x)＝ex＋lnx－2x,其中x＞0,故h′(x)＝

设s(x)＝ex－x－1,x＞0,则s′(x)＝ex－1＞0,故s(x)在(0,＋∞)上为增函数,故s(x)＞s(0)＝0,即ex＞x＋1,所以,所以h(x)在(0,＋∞)上为增函数,而h(1)＝e－2＞0,,故h(x)在(0,＋∞)上有且只有一个零点x0,且

当0＜x＜x0时,h(x)＜0,则ex－x＜x－lnx,即f(x)＜g(x).

当x＞x0时,h(x)＞0,则ex－x＞x－lnx,即f(x)＞g(x),因此若存在直线y＝b与曲线y＝f(x),y＝g(x)有三个不同的交点,故b＝f(x0)＝g(x0)＞1,此时ex－x＝b有两个不同的零点x1,x0(x1＜0＜x0),x－lnx＝b有两个不同的零点x0,x4(0＜x0＜1＜x4),故ex1－x1＝b,ex0－x0＝b,x4－lnx4－b＝0,x0－lnx0－b＝0,所以x4－b＝lnx4,即ex4－b＝x4,即ex4－b－(x4－b)－b＝0,故x4－b为方程ex－x＝b的解,同理x0－b也为方程ex－x＝b的解.

又ex1－x1＝b可化为ex1＝x1＋b,即x1－ln(x1＋b)＝0,即(x1＋b)－ln(x1＋b)－b＝0,故x1＋b为方程x－lnx＝b的解,同理x0＋b也为方程x－lnx＝b的解,所以{x1,x0}＝{x0－b,x4－b}.而即x1＋x4＝2x0,x1,x0,x2成等差数列.

方法2设F(x)＝f(x)－g(x)＝ex－2x＋lnx,有

则F(x)在(0,＋∞)上单调递增,且F(1)＝e－2＞0,,所以F(x)在上有唯一的零点x0,使得F(x0)＝0,即f(x)与g(x)有唯一交点P(x0,y0).当y＝b经过点P时,y＝b与f(x),g(x)的三个交点横坐标分别为x1,x0,x2(x1＜0＜x0＜1＜x2),在y＝f(x)上有ex1－x1＝ex0－x0＝b,即f(x1)＝f(x0),在y＝g(x)上有

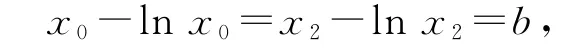
则elnx0－lnx0＝elnx2－lnx2＝b,即f(lnx0)＝f(lnx2)＝b,故必定有x1＝lnx0,x0＝lnx2⇒x2＝ex0,且f(x0)＝g(x0),即ex0－x0＝x0－lnx0,则x1＋x2＝2x0,即x1,x0,x2成等差数列.

本题第(1)问是大部分学生能够得到分数的.时间来不及的学生,也可以通过猜想和验证,得到一点分数.但第(1)问,要拿满分,需要分类讨论.第(2)问,则需要严谨证明.在全卷多题把关的情况下,第22题取得满分,实属凤毛麟角了.本题要求学生在面对综合性较强且情境较为复杂、新颖的问题时,要具有探究能力与创新精神.本题中考查了分类讨论、函数与方程的思想,体现了一般与特殊的转化思想.

2022年全国新高考Ⅰ卷数学试题从高考数学评价体系出发,秉承重基础、重本质,贴近中学数学教学的一贯命题思路.试题背景熟悉,梯度设置合理,符合在新高考背景下一线师生的预期.试题简约而不简单,深刻而不深奥.试题大气、大道,题干简洁明了,同时还充分吸取了前两年新高考试卷在数学命题上的经验,实现了稳中有变,变中有新.试题取材源于教材、生活,考查的终极目标服务于学生未来的可持续发展,能力立意,素养导航,对推进新高考改革、引导中学数学教学有着积极的作用,打造了数学高考试题新形态.

(完)