赏析数学核心素养视角下一道高考函数零点真题
2022-09-03王斌斌
王斌斌
(甘肃省静宁一中)
函数的零点问题是函数与方程中的重要内容,主要涉及已知函数零点求参数范围.若方程可解,则可以通过解方程求得参数的取值范围,但有时会遇到方程难以求解甚至不可求解的情况,此时可以通过构造函数,将问题转化为两个函数图像的交点问题.
母题(2020 年天津卷9)已知函数f(x)=若函数g(x)=f(x)-|kx2-2x|(k∈R)恰有4个零点,则k的取值范围是( ).
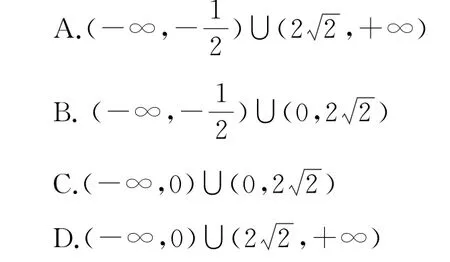
解析由g(0)=0,结合已知将问题转化为y=|kx-2|与有3 个不同的交点,再分k=0,k<0,k>0这三种情况讨论即可得到答案.
注意到g(0)=0,所以要使g(x)恰有4个零点,只需方程恰有3 个实根即可.令,则y=|kx-2|与的图像有3个不同的交点.
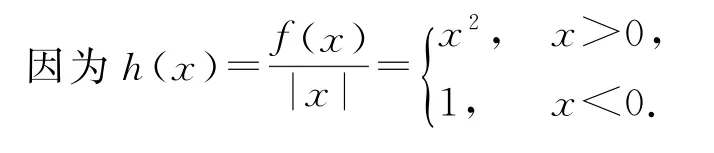
当k=0 时,此时y=2,如图1 所示,y=2 与有1个交点,不满足题意.
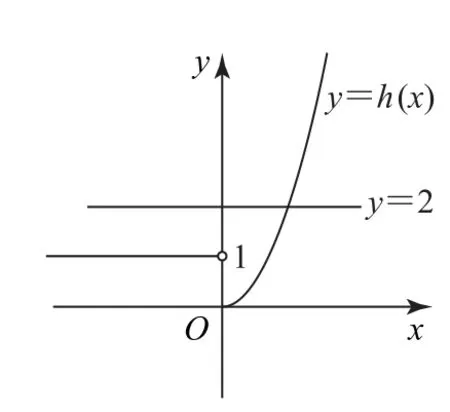
图1
当k<0 时,如图2 所示,此时y=|kx-2|与有3个不同交点,满足题意.
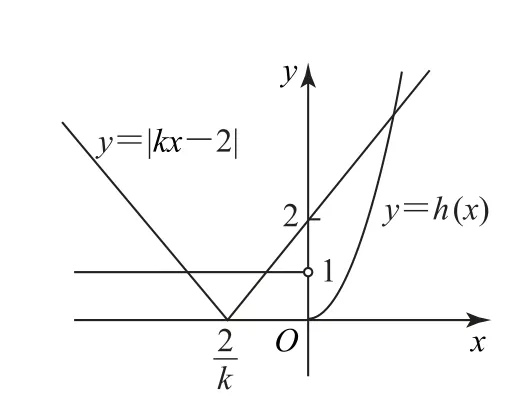
图2
当k>0时,如图3所示,当y=kx-2与y=x2相切时,联立方程得x2-kx+2=0.
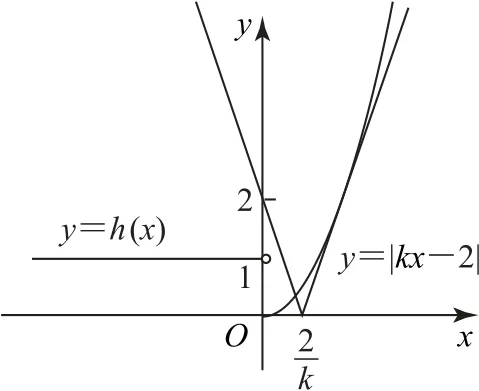
图3
令Δ=0,得k2-8=0,解得(负值舍去),所以
【数学建模】本题所设计的模型主要有两个,一是函数的构造,这里需要根据方程的形式进行合理的转化;二是考查了函数模型中的分段函数模型,分段函数作为中学的一个重要函数,能够较好地考查学生的推理论证能力.
【数学运算】本题思维量较大,首先要讨论题目中的参数,再对各类情况进行讨论,要求学生能够正确地进行相关运算.
【逻辑推理】在此问题的求解过程中,要能够对k=0,k>0和k<0这三种情况进行分析,正确地画出函数图像,从而准确地求出参数的取值范围.
【空间想象】本题主要考查函数与方程的应用,考查数形结合思想、转化与化归思想,是一道中档题.解题的关键就在于能够正确地绘制函数图像,这里间接地考查学生的空间想象能力.
其实,分析近年来的高考试题,不难发现,以分段函数为模型,以零点个数为载体考查参数的取值范围是天津卷高考试卷中的常考试题,独具特色.
例1(2021年天津卷9)设a∈R,函数

若f(x)在区间(0,+∞)内恰有6个零点,则a的取值范围是( ).

解析因为x2-2(a+1)x+a2+5=0最多有2个根,所以cos(2πx-2πa)=0至少有4个根.由,可得(k∈Z).由,可得

若x≥a,则f(x)=x2-2(a+1)x+a2+5,所以

当a<2时,Δ<0,f(x)无零点.
当a=2时,Δ=0,f(x)有1个零点.
当a>2时,令f(a)=a2-2a(a+1)+a2+5=-2a+5≥0,则,此时f(x)有2个零点,若,f(a)<0,则f(x)有1个零点.

本题的2020年天津卷的高考真题相类似,考点相同.首先由x2-2(a+1)x+a2+5=0最多有2个根,可得cos(2πx-2πa)=0至少有4个根,分别讨论当x<a和x≥a时两个函数零点的个数情况.
点评例2函数f(x)是定义在R 上的奇函数,且f(x-1)为偶函数,当x∈[0,1]时,,若函数g(x)=f(x)-x-b有3个零点,则实数b的取值范围是( ).

解析因为函数f(x)是定义在R 上的奇函数,且f(x-1)为偶函数,所以f(x-1)=f(-x-1)=-f(x+1),则f(x-1)=f(x+3),所以f(x)的对称轴为x=-1且周期为4,函数f(x)的图像如图4所示.

图4
g(x)=f(x)-x-b有3个零点,即函数f(x)与函数y=x+b有3个交点.当x∈[0,1]且直线y=x+b与函数f(x)在点(0,1)处相切时,有2个相等的实数根,即x2+(2b-1)x-b2=0有2个相等的实数根.
由Δ=0,求得.由数形结合可得g(x)=f(x)-x-b有3个零点时,实数b满足,故求得b的取值范围为
再根据函数f(x)的周期为4,可求得b的取值范围为(k∈Z),故选C.
(完)
