声速不确定条件下的运动水下航行器自定位

贾天一, 高婧洁, 申晓红, 刘宏伟

(1. 西安电子科技大学雷达信号处理国家重点实验室, 陕西 西安 710071;2. 西北工业大学航海学院, 陕西 西安 710072; 3. 长安大学信息工程学院, 陕西 西安 710064)

0 引 言

水下航行器的高精度自定位在导航、监视、海底测绘、水下搜救等诸多应用中具有至关重要的作用。一般情况下,航行器可通过自身装备的惯性导航或航位推算系统使用惯性测量单元(inertial measurement unit, IMU)或多普勒速度仪(Doppler velocity logs, DVL)来估计航行器的位置。然而,这一类方法很难避免位置误差的无限累积。由于这种累积误差会随着时间的增长而无限制增长,如果长期不采用其他技术进行校正,定位误差将继续增大,导致定位性能随着运行时间的增长而下降。因此,在一些水下长时间的任务场景中,需要通过其他方法进行位置校正。

一种方法是通过全球定位系统(global positioning systems, GPS)进行位置校正。但是由于传播介质水对电磁波的强衰减作用,GPS的电磁波信号在水下只能传播几米的距离。进而导致航行器必须上浮至水面附近才能接收到GPS信号。这种操作,尤其是在深海情况下,是非常耗能费时的。另一种方法是利用水下声学定位系统,例如长基线(long baseline, LBL)系统进行航行器定位。这类系统通过测量航行器与已知位置应答器之间的双程传播时间(two-way travel time, TWTT)来进行定位,这种定位机制可以克服上述惯性导航定位方法的缺陷,能够提供一个有界的、长期的高精度定位。但同时,该类方法的定位精度也会受到时间测量噪声和水声信号传播速度不确定的影响。

针对运动水下航行器自定位的研究尽管已经取得了许多进展,但是为了简化研究,通常会忽略测量周期内航行器运动带来的影响。在测量周期内,由于水声信号的长传播时延以及航行器的运动特性,造成航行器接收到来自不同应答器回复信号的位置并不相同,并且航行器位置的变化与航行器运动速度和信号传播时间有关。现代的水下航行器往往具有高速行驶能力,在测量周期中忽略航行器的运动是导致其定位性能下降的主要因素之一。

已有研究验证了在定位中考虑航行器运动可有效提高定位性能。文献[20]利用扩展卡尔曼滤波(extended Kalman filter, EKF)构造了一种组合导航算法,并进行了实验验证。文献[21]提出了一种贝叶斯方法来补偿航行器运动，以获得更好的定位精度。文献[23]和文献[24]分别提出了运动航行器位置估计的近似解和修正解。但是包括上述方法在内的传统方法尚未考虑声速不确定带来的影响。

在水下环境中,声速会随着温度、盐度和深度的变化而变化。这意味着声速既是时变的，也是空变的。因此,针对声速的不确定性,一些研究者提出将声速建模为未知的确定性常数,即声速完全未知,需要结合测量进行估计;还有一些研究者采用声速剖面进行建模,用于构建声速的空间特征。尽管声速剖面只是关于深度的函数,但该模型仍然很复杂。

针对水下复杂环境的声速建模,本文假设在一个很短的测量周期内,声速是与时间无关的未知常数。在每个测量周期内,可以获得声速的名义值(例如可采用水下航行器上装备的声速测量仪获得)。但是由于水下复杂环境因素和测量方法限制,获得的名义声速通常存在误差,因此本文将声速名义值建模为真实值的测量值,即测量的声速受到了噪声的污染。本文基于该假设研究声速不确定条件下的运动航行器定位问题,利用加权最小二乘(weighted least squares, WLS)方法估计航行器位置，研究利用最大似然(maximum likelihood, ML)估计法将获取的声速更新为更准确的值。

1 信号模型

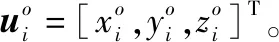
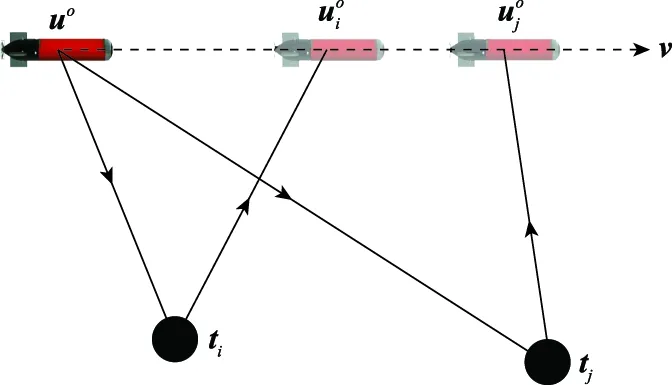
图1 运动航行器自定位场景Fig.1 Localization scenario of a moving vehicle

假设应答器的反应时间和信号处理时间可以忽略不计,信号传播时间的真实值可表示为

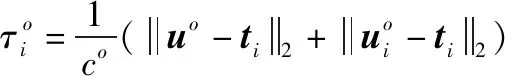
(1)

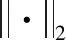
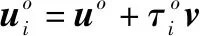
(2)

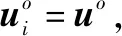
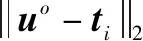
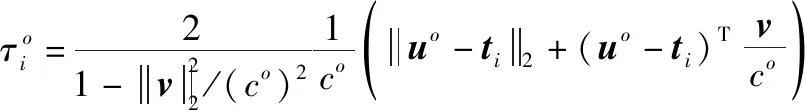
(3)

然而,测量航行器获取的传播时间会受到噪声的污染,将获取的个时间测量表示为向量形式

=[,,…,]=+Δ

(4)

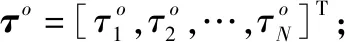
前文已经提到,如水下环境中，很难准确测量声速。由于受到温、盐、压等因素的影响,声速是时变空变的。因此,在定位中航行器不可能获得声速的真实值,获取的只是声速的单次测量值。本文将获取声速建模为关于真实值的观测:

=+Δ

(5)

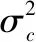
2 基于WLS的目标定位方法

2.1 第一步求解

对式(3)进行变形,可以得到

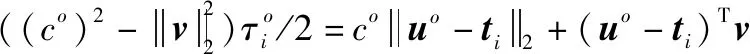
(6)

将(-)移到等式左侧,两边同时平方后整理可得

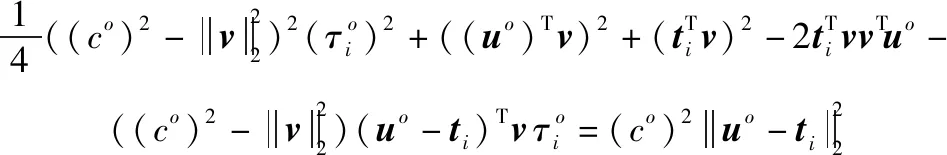
(7)

(8)

式中:

(9)

(10)

式中:

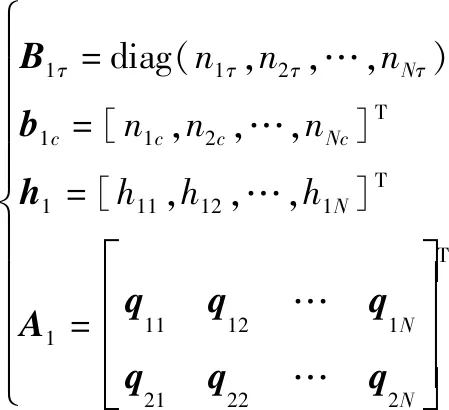
式(10)的WLS解可以表示为

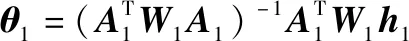
(11)

其中,加权矩阵可由下式计算得到:

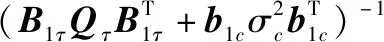
(12)

需要注意的是，由于加权矩阵依赖于位置真实值,在计算时可首先将近似为单位阵,通过式(11)计算出一个初始值,然后更新后，再利用式(11)计算得到第一步的最终结果。

2.2 第二步求解

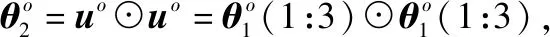
(13)

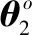
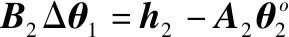
(14)

式中:

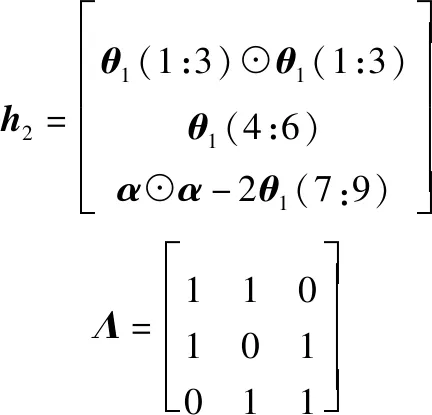
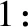
式(14)的WLS解可以表示为

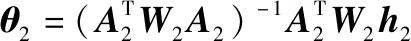
(15)

其中,加权矩阵可由下式计算得到:

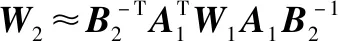
(16)

航行器位置的最终估计结果可由下式计算得到:

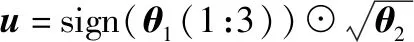
(17)

其中，符号函数sign为了保证最终估计的位置结果，正负号与第一步计算结果一致。

3 基于ML估计的声速更新方法

上述基于WLS的定位方法只能求解目标位置,事实上,可以联合时间观测和声速观测进一步更新声速。本节将利用ML估计法更新声速。时间测量和声速的联合分布密度函数可写为

(,)=(|)()

(18)

式中:表示时间测量的似然函数;表示声速的分布函数。对式(18)取对数后并忽略常数项,可得

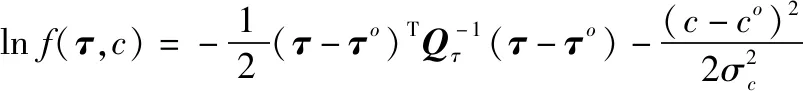
(19)

定义未知变量=[(),],对其进行变形可得关于未知变量的目标函数:

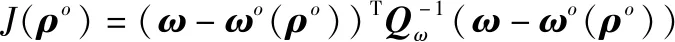
(20)

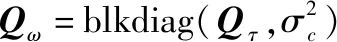
对于式(20),可以采用Gauss-Newton迭代法求解,迭代公式可写为

(21)

式中:

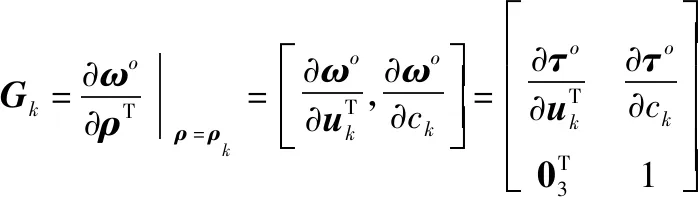
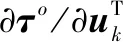
式(21)中的初始值可通过前文基于WLS的目标定位方法以及声速测量给出,即=[,]。

事实上,在ML估计法中,除了可以返回声速估计外,也可以返回位置估计。该位置估计结果和WLS的估计结果几乎不存在差异,并且根据大量仿真实验结果可知,二者在小噪声条件下均可以达到克拉美罗下界(Cramer-Rao lower bound, CRLB)。另一方面,ML估计法也可以直接实现两个参数的同时联合估计,但是ML估计受限于初始值的选取。本文利用WLS方法提供位置估计,作为算法初始值,以获得声速的更新。

4 理论性能

理论性能主要包括理论定位精度和提出算法的复杂度分析。理论定位精度主要通过CRLB来描述,算法复杂度主要通过涉及的乘法运算次数衡量。

4.1 CRLB

CRLB建立了无偏估计误差协方差矩阵的下界。下面推导位置向量和声速的CRLB。定义未知变量的CRLB矩阵为

(22)

代入式(19),并取期望可得

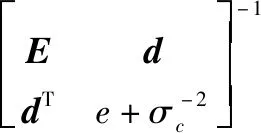
(23)

式中:

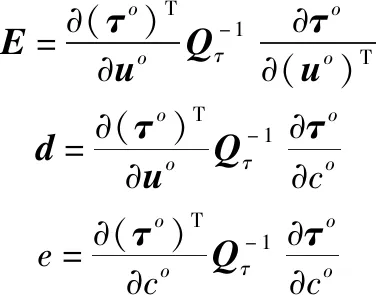
∂()∂的第列和∂∂的第个元素为

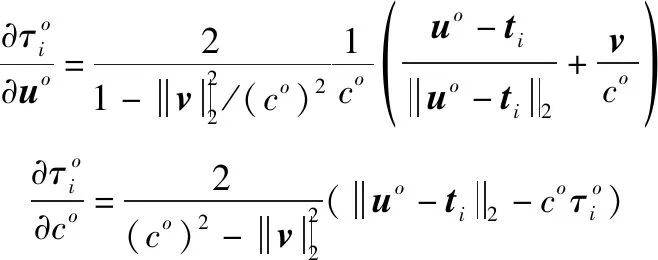
对式(23)利用分块矩阵求逆公式,可得目标位置和声速的CRLB分别为

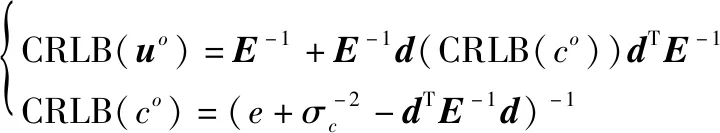
(24)

4.2 算法复杂度

WLS方法的计算效率主要受到第一步中矩阵求逆的影响,其复杂度可近似表示为(),其中表示应答器数目。ML估计法主要受到迭代次数和每次迭代中的求逆运算影响,其复杂度可近似表示为((+1))。可以看出,ML估计法的复杂度较大,特别是当迭代次数增加时。

5 仿真实验和结果分析

仿真中,采用9个应答器,其坐标位置详见表1。

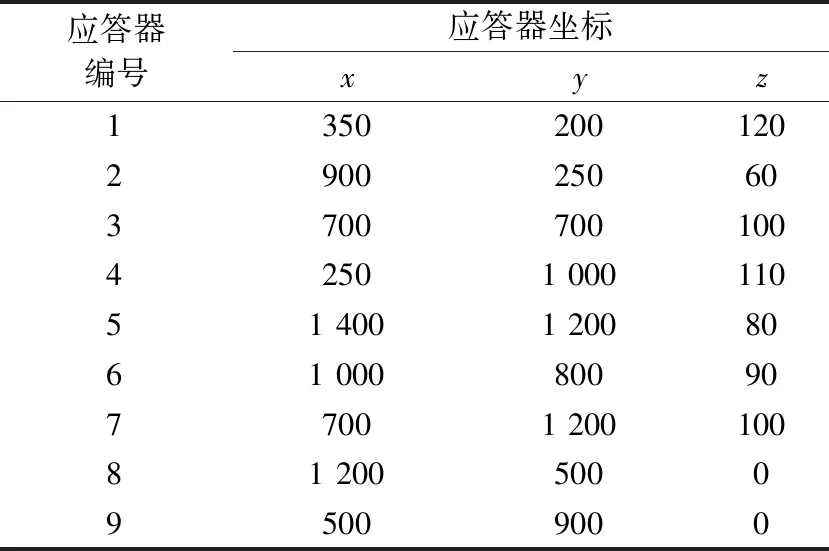
表1 应答器坐标位置Table 1 Positions of transponders m

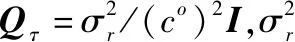
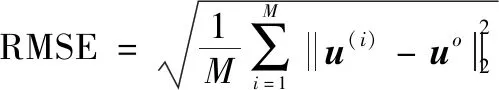
(25)

式中:()表示对真实值的估计量;表示蒙特卡罗实验次数。除非特别说明,本文中一般取=5 000。在仿真中，对文献[25]中的联合(位置和声速)估计法。文献[23]中的运动航行器定位近似解以及文献[24]中的运动航行器定位修正解的性能进行了对比。

5.1 定位结果和分析

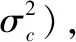
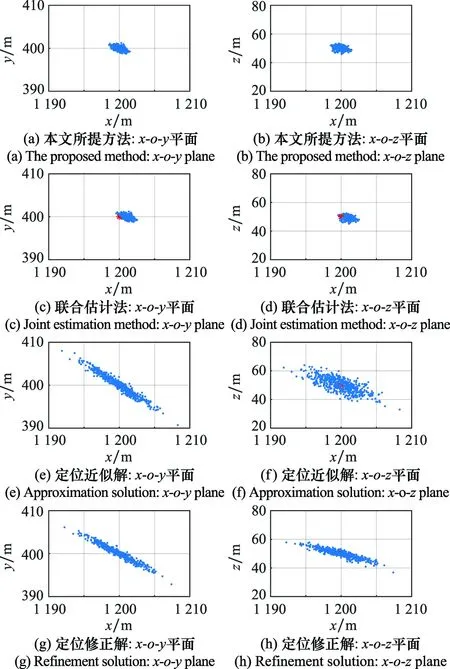
图2 500次蒙特卡罗实验定位结果分布图Fig.2 The output distribution of different methods obtained from 500 Monte Carlo simulations

图3给出了各个方法在距离测量方差增加时的定位性能。声速标准差设置为=5 m/s,航行器运动速度为10 m/s。可以看出,本文所提的方法,即基于WLS的目标定位方法,在距离测量噪声不大(小于10m)时都可以达到CRLB,而文献中已有方法的性能均不理想,特别是在小噪声时,3种方法都不能达到CRLB。具体原因如下:文献[25]中的联合估计法,可以通过时间测量同时估计目标位置和信号传播速度(声速)。但是该方法是基于静态的定位情景提出来的,即在定位模型中忽略了航行器的运动,从而导致面向运动航行器定位时,定位精度不高。尽管文献[23]的修正解和文献[24]的近似解都是针对运动航行器的定位解,但是二者均未考虑声速不确定性对求解方法的影响,因此定位性能较差。

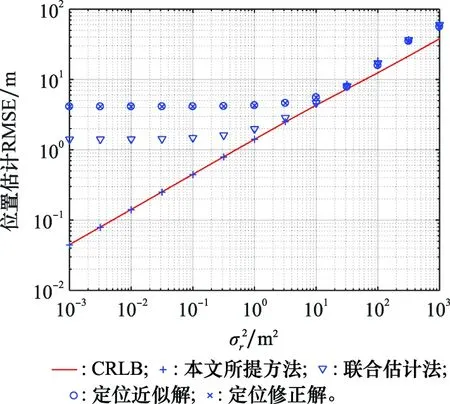
图3 距离测量方差对定位性能的影响Fig.3 Effect of range measurement variance to localization performance

图4给出了声速标准差增加时,不同方法的定位性能,其中距离测量噪声参数设置为=1 m,航行器运动速度为10 m/s。总体可以看出,本文所提方法在图中所示的参数变化范围内,都可以达到CRLB。而定位近似解和定位修正解由于在模型中没有考虑声速的不确定性,所以RMSE随着声速标准差的增大而明显增大。当声速标准差接近于0时,二者性能接近于本文所提方法的定位性能。联合估计法将声速视为未知量,其定位性能不会受到声速标准差的影响。

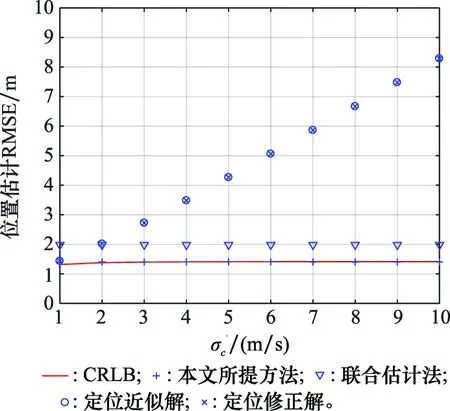
图4 声速标准差对定位性能的影响Fig.4 Effect of sound speed standard deviation to localization performance

图5给出了航行器运动速度增加时,不同方法的定位性能,其中距离测量噪声参数设置为=1 m,声速标准差设置为=5 m/s。同样,本文所提方法在所示速度范围内,均可达到CRLB。由于联合估计法基于静态定位情景,忽略了航行器的运动,其定位性能主要受到航行运动速度的影响,且随着运动速度的增大,定位性能下降。当航行器运动速度接近于0时,联合估计方法的定位性能接近于本文所提方法的性能。由于定位近似解和定位修正解都是针对运动航行器的定位解,因此二者性能并未受到航行器运动速度变化的影响。

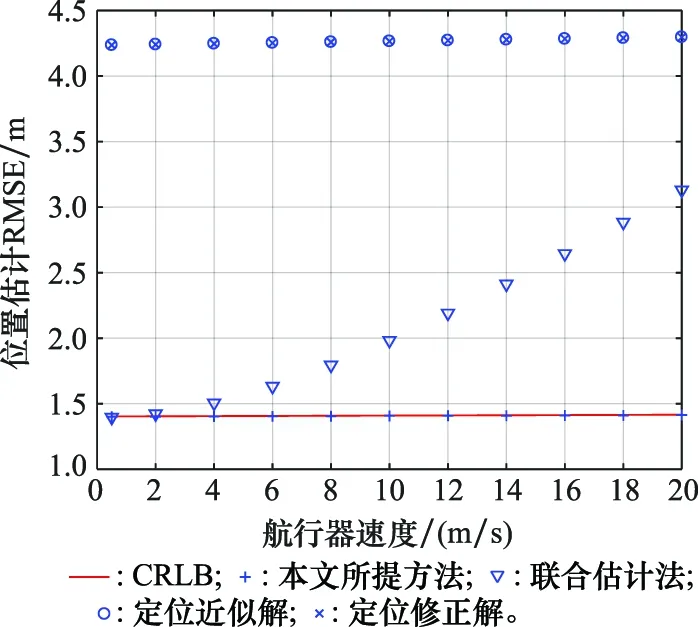
图5 航行器运动速度对定位性能的影响Fig.5 Effect of vehicle motion speed to localization performance

5.2 声速更新结果和分析

上述涉及的3种已有算法中,只有联合估计法可以估计声速。因此,本小节对比联合估计法,研究本文所提基于ML估计的声速更新性能。声速仿真结果图例中的“CRLB”表示本文第4节中推导的CRLB,而图例中“声速完全未知的CRLB”是在假设声速完全未知的定位情景下,仅通过时延测量信息同时估计目标位置和声速时,声速所对应的CRLB。

图6给出了距离测量噪声对声速更新的影响,仿真参数设置与图3相同。可以看出,本文所提方法在所示噪声方差变化范围内都可以达到CRLB,并且在噪声不大(小于10m)时,声速更新的RMSE优于原始声速标准差(5 m/s)。而联合估计法未能达到CRLB,但是其声速估计性能在噪声较小时保持恒定,在噪声较大时接近于声速未知时的CRLB。

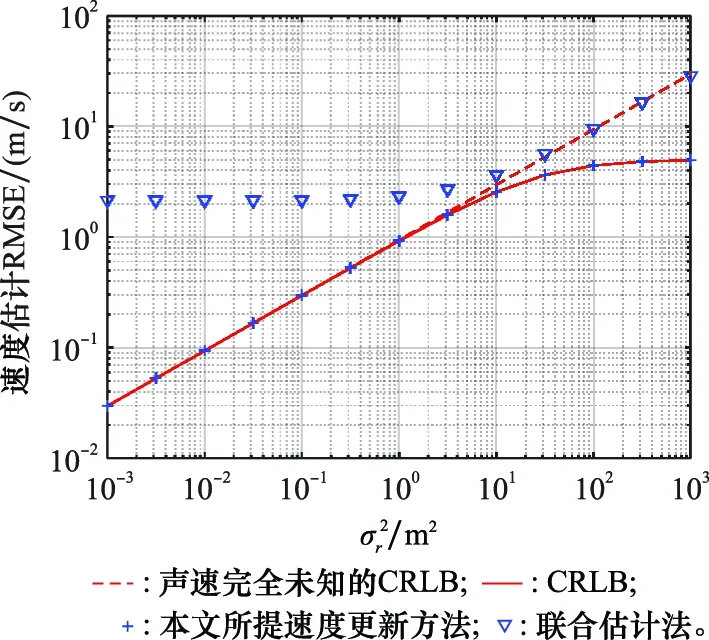
图6 距离测量方差对声速更新的影响Fig.6 Effect of range measurement variance to sound speed update

图7展示了声速标准差对声速更新的影响,其仿真参数设置与图4相同。联合估计法的声速估计性能未能达到CRLB,但性能维持恒定。本文所提方法的声速估计性能受声速标准差影响不明显,特别是在声速标准差相对较大时,此时的性能接近于声速未知时的CRLB。也就是说,在声速标准差很大时,相比于时间测量,由声速测量获得的信息几乎可以忽略不计,此时可将声速视为未知量。

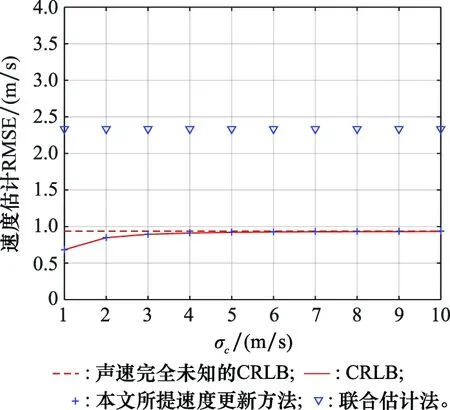
图7 声速标准差对声速更新的影响Fig.7 Effect of sound speed standard deviation to sound speed update

图8展示了航行器运动速度对声速更新的影响,其仿真参数设置与图5相同。联合估计法的速度估计主要受到航行运动速度的影响,且随着运动速度的增大性能下降。当航行器运动速度接近于0时,联合估计方法的性能接近于本文所提方法的速度估计性能。这一结论与图5所得定位性能结论一致。

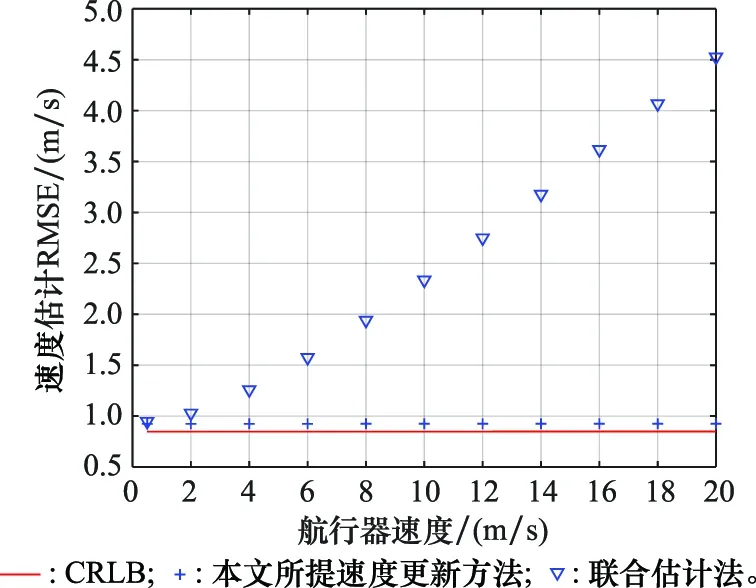
图8 航行器运动速度对声速更新的影响Fig.8 Effect of vehicle motion speed to sound speed update

6 结 论

本文针对声速不确定条件下的运动水下航行器自定位问题,构建了运动状态下的时间测量定位模型,并对声速不确定性建模。推导了基于WLS的目标定位方法和基于ML的声速更新方法。仿真结果验证了相比于文献已有的联合估计法、定位近似解和定位修正解,本文所提定位方法在各种仿真条件下性能突出,均能达到相应的位置估计CRLB;而相比于联合估计法给出的声速估计结果,基于ML的声速更新方法也能达到声速估计的CRLB。综上所述,本文所提方法提升了现有方法的定位性能。