基于解析几何理论的FAST 形状特殊位置理想抛物面预测

张 迪，裴智明，靳谦诚

（太原理工大学机械与运载工程学院，山西 太原 030024）

FAST 主要由主动反射面、馈源舱及控制、测量和支承系统组成。主动反射面由主索网、反射面板、下拉索、促动器及支承结构等构成可调节球面。主索网以三角网格用主索节点构成，三角板上安装反射面板，主索节点连接单根下拉索，下拉索与促动器连接，通过促动器拖动下拉索下的节点，用以控制反射面的形状。馈源舱以机电一体化平台支撑和Stewart 系统装置调节[1-2]。本文经过数学分析和科学建模，基于FAST 最佳接收比，主动反射面的形状调节问题，通过建立空间理想抛物面的几何模型、促动器调节下的关联理论以及采用非线性规划策略和寻优算法，对2226 个主索节点进行简化与规划，对FAST 实现自主反射面变形的网面调整策略模型，分析了基于费马原理三维空间光线反射的馈源舱接收比，实现了FAST 自动控面的相关工作要求。

本文总体思路是在促动器调节的约束下，带动下拉索和主索节点的运动，找到理想抛物面后，调整促动器的伸缩量，将反射面变形为主反射面，且尽量贴近理想抛物面，以使天体电磁波经反射后馈源舱的接收效果最好。

1 数据预处理

为了使主反射面板能够完美反射，本文选取天体位置在最特殊情况下，即：α=0°，β=90°时（天体的方位以α，β 量化描述），需给出在满足主反射面板调节约束条件下的理想抛物面位置，即相应形状[3-4]，指导以促进器为主的主索节点调节方式。满足调节因素的影响有以下5 个方面。

1） 主索节点调节后，任意相邻节点的距离必然会发生变化，为了满足各方面要求，考虑到应力、变形以及材料的力学性能等各方面因素，需要限制任意相邻两节点的变化不超过0.07%。

2） 根据题目要求和相关资料显示，下拉索用于主索节点和促动器的连接，故其长度不会发生变化，且规定了促动器的伸缩范围为-0.6 m～+0.6 m。

根据给出的所有主索节点的坐标，均以基准面球心C（0，0，0） 作为坐标原点，再有A0（0，0，-300.4） 为最低的主索节点的位置坐标。

3） 基准球面和抛物线面的口径相同均为300 m。

4） 每块反射三角形面板均为基准球面的一部分，根据相关资料显示，反射面板上开有小圆孔（直径d＜5 mm） 用以漏雨水。由于孔径小，几乎不影响电磁波反射，因此在模型分析建立与求解时设定其面板无孔。

5） 在基准态基准面上，所有的主索节点将在基准球面上，考虑到主索节点的点径远小于三角反射面板的尺寸，因此可以设定反射面的顶点即为主索节点，经相关分析演算，差值偏移率远远小于0.000001 26%。

2 建立FAST 基于解析几何理论的特殊位置时理想抛物面的优化变形几何模型

由于馈源舱中心P 只能在与基准球面同心的焦面上运动，因此，P 位于被测天体与基准球面中心连线SC 和焦面的交点位置，而理想抛物面可以看作抛物线绕其公转轴旋转而形成。根据相关抛物线知识可知：P 点即为其焦点。而SC 和基准球面的交点O 是形成该旋转抛物面的抛物线顶点。

球面和抛物面都具有各向同性的特点，因此在建立相关分析模型时，可将特殊位置的几何形状模型简化到二维空间进行描述：可用圆弧代替球面，用抛物线代替抛物面[5-6]。

其中要求球面与抛物面口径相同均为R=300 m。

3 基于解析几何理论的特殊位置理想抛物面的优化变形几何模型的求解结果策略最优选择

根据资料显示可以建立三种策略模型，分别为标准式、下偏式以及查阅式，在此进行模型建立和比较。

1） 标准式：当最低点的偏移距离h=0 m 时，按照题目要求F=0.466R 时，利用抛物线和旋转抛物面相关理论，利用MATLAB 工具得出理想抛物面的几何解析表达式为

以标准式方程分析，可做出空间内三维理想抛物面，其口径为300 m，最低点与基准球面相重合一点。为了更加清晰直观的观测理想抛物面与基准面的相互位置关系，利用MATLAB 工具可做出三维空间的FAST 理想抛物面与基准球面位置图，见图1。

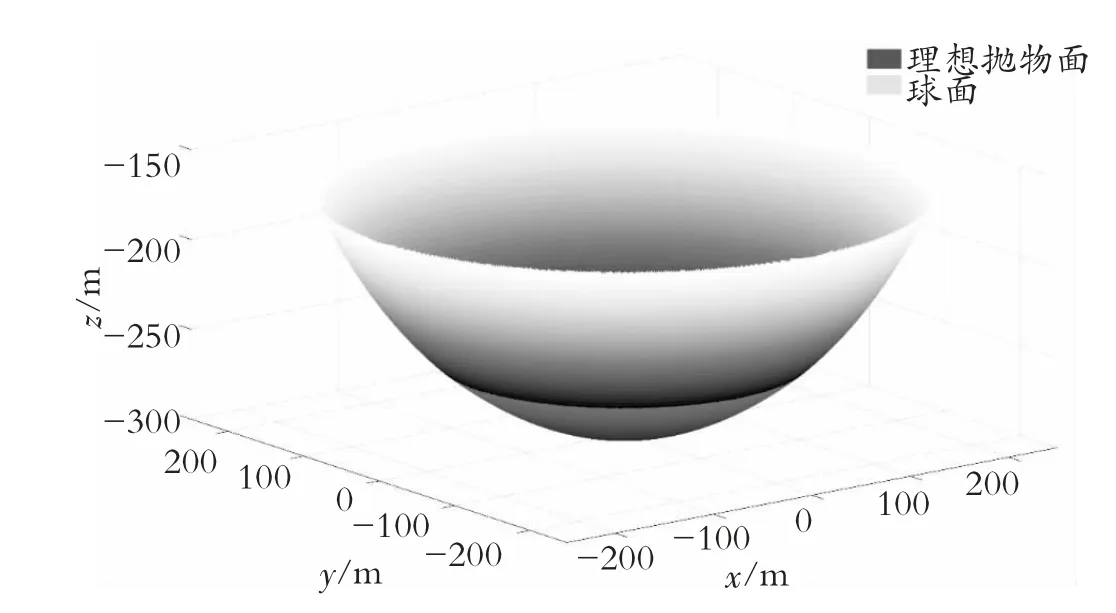
图1 标准式下的理想抛物面与基准球面嵌套的形状和位置

2） 下偏式：当最低点的偏移距离h=-0.2 m时，按照题目要求F=0.466R 时，利用抛物线和旋转抛物面相关理论，利用MATLAB 工具得出理想抛物面的几何解析表达式为

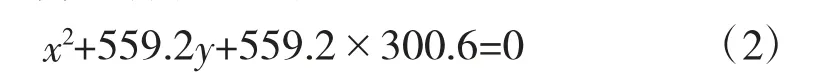
以标准式方程分析，可做出空间内三维理想抛物面见图2，其口径为300 m，最低点与基准球面相差h=-0.2 m。

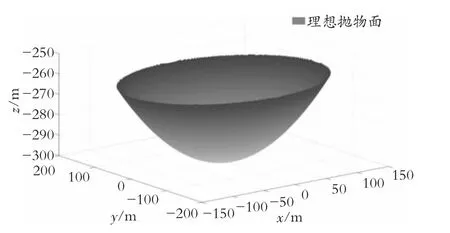
图2 下偏式下的理想抛物面的形状和位置

3） 查阅式：当最低点的偏移距离h=0 m 时，按照查阅相关资料显示，要求F=0.4665R 时，利用抛物线和旋转抛物面相关理论，利用MATLAB 工具得出理想抛物面的几何解析表达式为

以标准式方程分析，可做出空间内三维理想抛物面见图3，其口径为300 m，最低点与基准球面相差h=0 m。

图3 查阅式下的理想抛物面的形状和位置

4 变形几何模型的模型结果检验及模型相关结论

根据模型分析可知，模型的最终结果要满足调节因素的约束条件，经检验下偏式和查阅式的促动器近似调节量见表1。

表1 下偏式和查阅式的促动器调节量的范围值（m）

根据基于解析几何理论的特殊位置建立的理想抛物面的优化变形几何模型及其模型分析，反射面变形从直观上可以得知，其边缘处与基准圆面的光滑性越好，则调节难度越小，精度越大。反之，在衔接处会出现较大的拉压载荷，造成较大的应力，使得工作过程极其容易出现疲劳现象。对连接的光滑性和工作强度以及疲劳性等影响因子进行综合考虑，在实际调节过程中就必须满足一定的约束条件才能使FAST 真正高效地运行。

因此，根据该模型可以得出以下基本结论。

一是下偏式类型的理想抛物面促动器的工作行程是最小的，为区间[0.0143，0.5377]且符合调节的范围。二是下偏式类型的理想抛物面节点总位移较小，使得基准球面和调节面板钢索的应力较小，有较好的抗疲劳性。三是下偏式类型的理想抛物面与基准球面的过渡相对平滑。

5 结束语

FAST 作为目前落成的最高效和功能最齐全的设备，在模型建立时更大程度地考虑到实际情况和目前研究的最新成果，对相关理论的建立给出了较为详细的理论推导和详细证明，使得结果更加完整可靠。在利用非线性规划确定实际促动器工作策略时，考虑到多变量最简便有效的规划算法，在相互关联多变量约束的条件下，且有非线性函数时，非线性规划优点已经很好的显现。然而考虑到模型的数据空间较大，在未输入相关限制时，随着搜索和运行的不断深入，计算量将会增大，因此，采用分阶段的方法进行逐步寻优，最终计算结果将十分逼近最优值，但仍有一定偏差。后续研究，需要深入FAST 的实际工作进程，以科学客观的角度将理论模型与实际工作状态相结合，充分考虑实际工作状态下的情况，以建立更为实用和可行的科学模型。