替代电镀铬SiC 复合镀电沉积机理综述

曹琳,李双建,王永喆,林琳,张鹏*,王启伟*

（1. 暨南大学先进耐磨蚀及功能材料研究院，广东广州 510632；2. 中国航发沈阳黎明航空发动机有限责任公司，辽宁 沈阳 110043）

耐磨性硬铬电镀镀层具有硬度高、膜基结合力强及摩擦系数低等优点而被广泛应用于机械零部件表面上，但是在硬铬电镀过程中产生的废水会对环境造成严重污染，因此复合电沉积工艺有望代替硬铬工艺而逐步受到重视。Metzger 等［1］设计了Wan⁃kel 发动机，并将SiC/Ni 复合涂层成功地用于汽车工业中的易损件上。SiC/Ni 复合涂层为非金属夹杂物和金属相复合沉积而形成的涂层，所形成的涂层的物理及机械性能得到很大提高，并且涂层与基体之间的结合力良好。常用陶瓷颗粒［2-12］来提高涂层 的 硬 度，如Al2O3、SiC、Cr2O3、TiO2、TiN、AlN、MoS2和WC 等。超细SiC/Ni 与粗SiC/Ni 复合涂层相比，具有更光滑的表面及更好的结合强度［13］。当SiC 颗粒直径大于0.1 μm 时，在SiC 表面会形成一层SiO2，SiO2会降 低SiC 与Ni 基 体的 结 合 力，并 且使涂层产生孔隙和裂纹。相比之下，超细SiC 的界面更完整，并且无缺陷。

根据Zener 方程，同样的体积颗粒含量，超细颗粒数量较多时可抑制基体晶粒的生长温度，但颗粒尺寸的减小也会减少共沉积涂层中粒子的含量。Maurin［14］的研究结果表明：在硫酸镍溶液中，当SiC粒径为0.1 μm 时，SiC 涂层中的SiC 质量分数小于0.7%，接近于检测EDX 分析的阈值；当粒径为0.8 μm 时，涂层中SiC 质量分数可达2%；粒径为2.85 μm 时，涂层中SiC 质量分数可达5%。所以，共沉积机理对涂层的硬质颗粒的含量以及指导涂层工艺是十分重要的，有必要进行研究。

固体颗粒如何进入基质金属中，以及基质金属与固体增强颗粒共沉积机理的问题一直争论不断。Brandes 等［15］认为，固体颗粒由电解液内部向阴极运动时，颗粒受到搅拌及电场力的共同作用，从而移动到阴极表面。也有人提出［16-17］提高颗粒表面吸附金属离子的量，可以提高颗粒向阴极表面的移动和吸附。总之，不同的研究者提出几种不同的观点，虽然每个机理都可合理地解释一些现象，但是也都存在片面性，不能解释所有复合电沉积现象。

1 微粒在镀液中的行为

不同种类的固体颗粒添加到镀液中，固体颗粒的粒度、导电性质和润湿性等因素都会影响镀层的质量。固体颗粒被浸润的过程，实际上就是液体与气体争夺固体表面的过程，这与固体颗粒的性质及表面能相关，其结果取决于固体颗粒及分散液体的极性差异。固体颗粒在液体中，可能出现固体颗粒分散或团聚两种状况。固体颗粒在镀液中聚集状态取决于颗粒间的相互作用及颗粒所处溶液中物理场和流体力学等因素，一般认为颗粒间的相互作用力包括分子间作用力、双电层静电作用力、溶剂化膜作用力以及吸附层的空间效应等［18］。

分子间作用力是颗粒在溶液中互相团聚的主要原因，对于同质颗粒，它们在镀液中的分子作用力总是表现为吸引力。静电作用力是由于镀层表面双电层所引起的，在镀液中颗粒表面选择溶解或选择性吸附而带电荷，相反电性的离子由于静电吸引而在颗粒周围的液体中扩散分布构成固体颗粒表面的双电层，这就是在液体中的颗粒周围出现双电层的原因。微粒在溶液中运动时，除双电层中的紧密双电层的电荷随着微粒一起运动外，微粒还将携带分散双层的部分电荷运动。对于同质颗粒，双电层静电作用力表现为排斥力，不同的颗粒表面电位往往不同值，如果是电荷异号的颗粒则表现为吸引力。溶剂化膜作用力，是由于粉体颗粒表面附近溶剂分子的重新排列所引起的。颗粒在液体中引起其周围液体分子结构的变化，称为结构化。当颗粒表面吸附有无机或有机聚合物时，聚合物吸附层将在颗粒接近时产生一种附加的作用，称为空间效应。当吸附层牢固而且相当致密，有良好的溶剂化胜质时，吸附层表现出很强的排斥力，称为空间排斥力，它对抵抗颗粒接近及团聚，此种力只有当固体颗粒间距达到双方吸附层距离接触时才出现［19］。

实际情况远比上述理论所描述的复杂。首先颗粒的相互作用与颗粒的表向性质，特别是润湿性有密切关系。其次，颗粒表面覆盖的吸附层的成分、覆盖率、吸附强度、层厚等也与颗粒之间的相互作用有密切联系。对于异质颗粒还可能出现分子作用力成为排斥力，而静电作用力成为吸引力的情况。并且，分子间作用力、静电力等表面作用力还与固体颗粒的粒径有关，与颗粒粒度的一次方成正比。随粒度的减小，其作用力也逐渐减小。对于几十微米以下的微细颗粒而言，各种表面力以及与表面有关的物理力都有可能起着主导作用。此外，由于固体颗粒处在重力场中，颗粒在镀液中还受到重力的作用。尽管重力对固体颗粒的团聚没有很大影响，但是对较为粗大的颗粒，例如毫米级的固体颗粒在镀液的悬浮和分散仍有重要的影响。当颗粒粒度小于毫米级时，随粒度的减小，重力作用下降很快，表面力则占据上风起支配作用。

在电沉积过程中，电极附近的溶液会存在浓度梯度，在特定条件下微粒会受到渗透力的作用，同时微粒还可能会受到憎水力的影响。这些作用力综合起来决定了固体颗粒在镀液中的行为变化。从复合电镀工艺角度看，希望固体颗粒在镀液中是完全均匀分散的稳定体系。通过选择合适的固体颗粒，可以很大程度上调控固体颗粒在溶液中的行为。此外，采用适量分散剂，并利用其与颗粒表面发生的相互作用，也能阻止固体颗粒在镀液中的团聚。事实上，无论哪种方法都很难做到让固体颗粒在镀液中真正的、完全的、均匀的分散。因此，在复合电沉积工艺中，常常采用搅拌方式来维持粉体颗粒在镀液中悬浮。

2 复合电沉积机理研究概况

众所周知，复合电沉积技术是通过电化学方法将一种或数种不溶性的小尺寸固体颗粒、惰性颗粒与金属离子发生共沉积，将颗粒包裹在基质金属中。金属离子在电极上还原为金属粒子。阴极反应的大致步骤包括液相中的物质传递、金属离子还原成金属原子及金属原子排列成一定构型的金属晶体。在镀液中加入固体颗粒后，电沉积过程变得非常复杂，如细小的固体颗粒对镀液中某些离子具有吸附作用，粉体颗粒之间以及固体与阴极表面之间也存在着相互作用。此外，溶液的流动也会对电沉积过程构成不同程度的影响。

自20 世纪70 年代，人们就先后提出了多种机理以试图揭示复合电沉积过程中作用机制，具有代表性的有以下三种机理。（1）吸附机理：该机理认为微粒只有在阴极上发生吸附时共沉积才能发生，微粒吸附在阴极表面后会被生长的金属带动嵌入基体中。（2）力学机理：该机理认为颗粒会被搅拌引起的力学运动所裹覆，流体动力因素和金属沉积速率会影响复合电沉积过程。搅拌引起的镀液运动，会增加微粒与电极间的碰撞频率，微粒被金属俘获的几率也随之增大。液流对电极的冲击作用，也会使原已停留在电极表面上的微粒脱离电极，重新进入溶液中。（3）电化学机理：该机理认为电极与溶液界面间场强和微粒表面所带电荷是复合电镀的关键因素，颗粒在镀液中的电泳迁移速率、颗粒穿越电极表面的分散层的速率、颗粒与电极表面形成的静电吸附强度，以及颗粒部分穿越电极表面的紧密层与吸附在颗粒表面的水化金属离子阴极还原，这些因素都会使颗粒表面直接与沉积金属接触而形成颗粒-金属。对于以上理论，人们很难形成一个统一的认识，这些理论只能对于某些体系或实验现象给予解释。如利用力学机理可以解释微观分散能力对复合电沉积的影响，以及不带电甚至是负电荷颗粒的复合共沉积，而电化学机理在这些现象中则显得无能为力。另外，对于搅拌因素对复合电沉积的影响，也只能用力学机理来分析。对于pH 值和温度等因素对复合电沉积的影响，用力学机理解释便行不通，而电化学机理可以给出合理的解释。在已有的复合电沉积机理的研究成果中，就当前有关复合电沉积过程主要有以下几种模型。

2.1 Guglielmi 模型

Guglielmi［2］认为，悬 浮在液相中的非导电颗 粒想要实现在阴极表面的共沉积，主要通过两个连续的吸附步骤：颗粒被带电离子及溶剂所包覆，在电极的紧密层外侧形成弱吸附，这一吸附实质为物理吸附且可逆，一般情况下发生弱吸附的微粒与悬浮于镀液中的微粒处于平衡状态；在界面电场的影响下，处于弱吸附状态的颗粒脱去表面所吸附的离子和溶剂化膜，颗粒的一部分进入紧密层内与电极直接接触，形成不可逆的电化学吸附，这一过程为强吸附，发生强吸附的颗粒被生长的金属所埋入而形成复合镀层。

通过理论推导，可用Guglielmi 模型表述颗粒在阴极表面的共沉积。

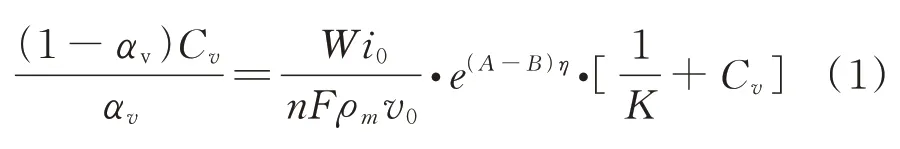
其中：ɑv为颗粒复合量，Cv是颗粒在镀液中的浓度；W、ρm、n 及F 分别为共沉积金属的原子量、密度、电子数和法拉第常数，i0为交换电流密度，A 为与金属沉积有关的常数；V0、B 是与颗粒共沉积相关的常数，K 是工艺操作相关的常数，η 是阴极的过电位。该模型将颗粒共沉积量、电极的电场力及悬浮于液相的颗粒浓度有机地结合起来，从电化学原理的角度来探讨微粒与金属共沉积的条件，提出了无机颗粒与金属共沉积的两步吸附理论。同时，该模型还反映了电极与溶液界面间电场的作用，将固相复合粒子浓度、液相悬浮粒子浓度及电极过电位有机地联系起来。模型的合理性己被多种复合电沉积体系所证实［20-22］，如果对该模型所提出的一些参量进行更深入的研究，有可能掌握住控制复合镀层形成的关键因素，这对复合沉积的理论发展显然有着重要意义。但是，Guglielmi 模型也存在一些问题。（1）假说不够全面、合理，其只考虑电场因素而没有考虑搅拌的力学因素。该模型认为弱吸附一旦变为强吸附，便被生长的金属嵌入，没考虑在共沉积过程中由于镀液搅拌会导致还未被金属埋牢固的强吸附颗粒的脱落，以及电沉积电流的大小、颗粒的尺寸与形状对颗粒共沉积的影响。（2）颗粒从弱吸附到强吸附需要一定的能量进而被生长的金属埋入，这些能量从何处来，强吸附颗粒又受到什么力，对这两个问题两步吸附理论无能为力。（3）不同粒径的微粒与金属共沉积时，即使微粒在镀液中的浓度相同，其沉积量也有相当大的差别。所以，这个理论无法揭示不同粒径的微粒在复合共沉积时存在的本质区别。

2.2 Celis（MTM）模型

J.P.Celis［23］等人在Guglielmi 模型的基础上，对颗粒与金属共沉积的机理又进行了更深入的研究，提出了Celis 模型，又称MTM 模型。在这一模型中，提出悬浮在镀液中的固体颗粒能够被阴极沉积金属俘获的基本条件，即吸附在固体颗粒表面上的阳离子能够在阴极表面被脱去，只有一部分颗粒能在阴极上被还原。该模型认为复合电沉积过程有五个步骤，即颗粒表面在镀液中形成离子吸附层、颗粒通过流体对流作用运动到流动边界层、颗粒通过扩散穿越边界层、颗粒在电极表面吸附、一定数量的吸附在颗粒上的离子还原导致颗粒被生长金属俘获。图1 为微粒共沉积的五个阶段。

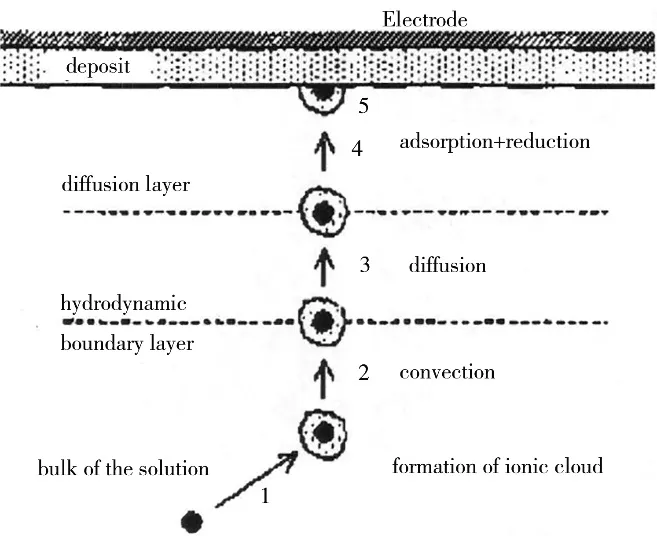
图1 微粒共沉积的五个阶段Figure 1 Five stages of particle co-desposion

在Celis（MTM）模型中，为计算颗粒在镀层中的质量百分含量Wt，建立了数学公式。

式（2）中，Wp为单个颗粒的质量（kg），i 为阴极电流密度，Np在电流密度i（s−1·m−2）下每单位时间和表面积在工作电极处穿过扩散层的粒子数量，P 为在电流密度i 处结合一个粒子的概率，ΔWm在电流密度i（kg·m−2·s−1）下每单位时间和表面积沉积的金属基体的质量。

Celis 模型具有积极的意义，其同时考虑了流体动力学因素和界面电场因素的影响，并且引入至数学模型中。同样，Celis 模型也存在一些缺点和错误，如：（1）该模型的五个步骤中没有阐明颗粒在阴极表面吸附作用的实际意义；（2）计算NP和P 时，曾假设自由离子和被颗粒吸附的离子运动和能量状态等同及颗粒与离子在扩散层传递速率相同，这些假说都是非常理想甚至是错误的，没有理论根据；（3）模型虽然考虑了流体动力学因素的影响，但数学处理过于简单；（4）在模型建立的过程中采用了许多限制性的前提条件，因此数学表达式中的参数P 很难定量计算。鉴于以上问题，该模型没有太大的实用价值。

2.3 Valdes 模型

Valdes［24］引进了“完全沉降”模型。该模型假定颗粒在到达电极表面一定距离内便被生长金属不可逆地俘获，在旋转圆盘电极上复合电沉积时颗粒在电解液中传质遵守质量平衡原则，在原来提出的对于颗粒数目浓度的连续性方程的基础上改进并提出该模型，以及导出了颗粒沉积的电化学速率表达式。

式（3）中，Cs是吸附在颗粒表面上电活性离子的浓度，k0为依赖于Cs的标准电化学反应速率常数（类似于交换电流密度），其他参数与电化学极化控制时极化公式中的相应参数的物理意义相同。

实际上这一模型建立的基础与Guglielmi 模型本质上等同的，因此存在Guglielmi 模型类似的弊端，而且Cs在理论上概念模糊，很难做出定量分析。

2.4 运动轨迹模型

运动轨迹模型［25］建立的出发点是考虑电极附近流体流动状况及颗粒在电极上所受各种力的作用。对于非布朗型颗粒，不考虑扩散影响，通过建立颗粒的运动方程，便可决定其轨迹方程。在旋转圆盘电极上，通过极限轨迹分析方法，便求得单位时间内碰撞到工作电极表面上的颗粒体积流量。该模型提出了滞留系数的概念，碰撞到电极表面上的某个颗粒被电极吸附并停留其上，其值大小依赖于作用在其上的粘附力和切向力之比。

运动轨迹模型精细地考察了电极表面颗粒所受各种作用力及流体场因素的影响，进一步深化了对于复合电沉积机理的认识。但运动轨迹模型也存在一些不足之处。（1）没有很好地分析界面电场的影响。（2）模型中只考虑了大微粒微米的复合共沉积过程，对更小的微粒不能给出其轨迹方程，也无法求出其向电极表面的传递速率。（3）该模型只能适用于层流场中复合电沉积微粒传质过程的分析，对于复合电沉积工艺通常的湍流场，微粒的传质便不可能得出定量解。

2.5 其他共沉积模型

Hwang［26］共 沉 积 模 型，该 模 型 是 对 理 论 的 改进，考虑了液相传质对反应机理的影响，以及吸附在颗粒表面的多种离子在速度决定步骤中的作用，这在复合电沉积模型中并不多见，但与其他模型一样，没有考虑非活性惰性颗粒与吸附态金属离子电化学还原之间的效率问题。该模型以酸性环境中复合电沉积为对象，研究了不同电流密度范围内的颗粒沉积速度，该模型能较好地解释了共析量与电流密度的关系曲线中出现两个峰值的现象，但尚未有其它适合体系报道。

Yeh 模型［27］等在研究复合电沉积时发现，沉积量的体积分数与电流密度关系曲线有一峰值。研究者认为，小电流密度时颗粒的复合沉积符合了两步转化模型，而在大电流密度时颗粒没有足够的时间在电极表面完成弱吸附过程就被包覆，因此速度控制不再是随后的强吸附过程而是颗粒向电极的传输步骤。由于颗粒的嵌入速度很快，所以假定电极表面附近镀液层中的颗粒均被不可逆包覆，此假设与模型的假设有相似之处。

以上几种研究机理的研究角度不同，它们各有侧重。因此，某种理论只能对共沉积过程中的某些现象给予较好的解释。到目前为止，还没有可以普遍适用于各种复合体系的共沉积理论，人们对复合电沉积过程以及共沉积理论尚需要进一步深入和广泛地研究。

3 结论

金属、陶瓷或聚合物复合颗粒的电沉积已经从成为一种不断发展和多样化的成熟技术，但沉积技术变量、沉积物质组成等都会相互影响，最终影响沉积涂层的质量。尽管这些年研究者们不断对复合电沉积涂层的质量和性能做了很多的研究，但颗粒到达阴极后以何种方式粘结其上，然后又是以怎样的模式或途径被捕获，研究者对这些关键性问题的认识目前还不完全清楚。目前，主要的几种复合沉积机理均有其各自的局限性。为了快速推进复合电沉积涂层发展，应该尽快丰富实验手段，对复合电沉积的本质过程进行观察和测试，改进多物理场计算机建模分析，并对上述数学模型进行修正和完善。