范德蒙矩阵在RS纠删码中应用的教学探微

许和乾，杜 炜

(合肥师范学院 数学与统计学院，安徽 合肥 230601)

近年来，随着科学技术的迅速发展，各种数据呈爆炸式增长，对于数据存储的可靠性需求也不断增强。2022年初，我国一体化大数据中心体系完成总体布局设计，“东数西算”工程正式全面启动。

高等代数作为数学专业本科阶段最重要的基础课之一，其教学内容对培养学生的创新精神、创新观念和创新能力起着不可替代的作用。研究基于一类特殊矩阵——范德蒙(Vandermonde)矩阵，探索如何通过研究性、探索性和开放性问题，以案例式、探究式或者是线上线下混合式等教学模式，培养学生的创新精神、创新观念和创新能力。

1 RS纠删码

为了防止数据丢失，通常有两种重要的方法：副本策略和编码策略。前者将原始数据拷贝成多份放置在不同的设备中；后者则是将原始数据分块并编码生成冗余数据块后存储，可以保证丢失一定数量之内的数据块，原始数据仍然可以恢复。副本策略随着数据量的增加，已经变得存储效率低下且费用昂贵。因此，编码策略越来越受到重视。

纠删码(Erasure Code)是编码策略的一种，它是存储领域常用的数据冗余技术，可以以更低的成本提供更高的可靠性，同时减小额外所需冗余设备的数量，从而提高存储设备的利用率。纠删码在分布式存储系统中的应用通常包括阵列纠删码(Array Code: RAID5、RAID6等)、RS(Reed-Solomon)类纠删码和低密度奇偶校验纠删码(Low Density Parity Check Code，LDPC)。其中，阵列纠删码和RS类纠删码主要运用于存储和数字编码领域；而LDPC码目前则主要应用于通信、视频和音频编码等领域。

RS码的基本原理如下：给定N个数据块，根据这些数据块生成M个校验块；对于任意的N和M，从N个数据块和M个校验块中任取N块都能恢复出原始的数据块，即RS码最多能容忍M个数据块或者校验块同时丢失。RS码的编译码过程建立在有限域之上：假定有k个数据符号m0,m1,…,mk-1需要存储，其中mi(0≤i≤k-1)均为有限域Fq中元素：通过构造多项式P(x)=m0x+m1x2+…+mk-1xk-1，再求该多项式P(x)在A={α1,α1,…,αn}⊆Fq上n个不同点处的取值，便可得到RS码的码字：

c=(c0,c1,…,cn-1)=(P(α1),P(α2),…,P(αn))

(1)

其中数据符号的数量k被称为该码的维数，n称为该码的长度。一个RS(n,k)码是指长度为n，维数为k的RS码。事实上，通过利用RS码对每k个数据符号进行编码，均能产生n-k个冗余，也就是校验符号。根据上述码字的构造方式，可得含有k个变量的线性方程组：

(2)

将其表示为矩阵形式，则有

(3)

式(3)左侧矩阵通常被称为RS码的生成矩阵。可以看出，只需知道码字c的任意不少于k个分量的值，上述方程组便存在唯一解，即可恢复k个数据符号。

RS码作为一种经典的MDS码因为达到了Singleton界，在保护数据不丢失或者丢失部分数据不影响整体功能的分布式存储系统中有很大的用处[1]，并广泛应用于Google分布式文件系统GFS、微软Azure云存储系统和Facebook HDFS中[2-4]。

2 范德蒙行列式的实践教学探索

2.1 课堂教学中的范德蒙行列式

范德蒙行列式在现行高等代数教材中，通常只是一道例题：

例1[5]：行列式

(4)

称为n阶的范德蒙行列式。可以证明，对任意的n(n≥2)，n阶范德蒙行列式等于a1,a2,…,an这n个数所有可能的差ai-aj(1≤j≤i≤n)的乘积。如果授课教师按照一般教学逻辑，只利用数学归纳法简单介绍其证明过程，就会导致学生难以理解该行列式的具体含义，无法做到学以致用，无法达到在课堂教学中培养学生创新精神这一根本目标。

2.2 基于范德蒙行列式，引入范德蒙矩阵

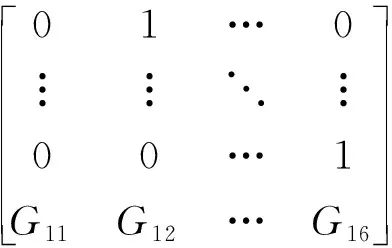
范德蒙矩阵是法国数学家范德蒙提出的一种各列为几何级数的矩阵。通常假定a1,a2,…,an为数域Fq中两两互异的数且不为0，则形如：

(5)

的m×n矩阵或其转置均称为范德蒙矩阵。教师可以在教学中通过范德蒙行列式，引入范德蒙矩阵。事实上，RS码的生成矩阵就是一个范德蒙矩阵。

可以看出，范德蒙矩阵的任一k阶子矩阵均可逆。当m=n时，就会得到一个n阶范德蒙方阵，其行列式即为例1中的范德蒙行列式。根据例1，对任意的n(n≥2)，n阶范德蒙行列式d=∏1≤j≤i≤n(ai-aj)。

2.3 范德蒙矩阵在RS纠删码中的应用

教师可以通过探索范德蒙矩阵在实际中的应用，让学生真切地感受到所学习的数学概念、数学知识都是来源于实践并扎根于实践中的，而不是所谓的“空中楼阁”。例如，Google GFS II(Colossus)中，便采用了最基本的RS(6，3)编码。将一个待编码的数据单元分为6个数据子块， 然后添加3个校验子块，最多可容忍包括校验子块在内的任意3个子块错误，其基本结构如图1所示。

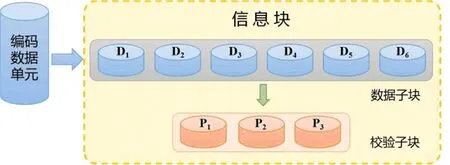
图1 纠删码结构示意图

利用一个“生成矩阵”G乘数据块D，从而建立数据块D和校验块P之间的联系；由于矩阵运算的可逆性，系统也就具备了容忍若干个数据块失效的能力。以下将利用矩阵的语言简单阐述RS(6，3)编码的基本原理。

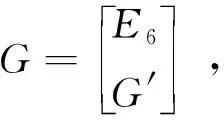
(6)

由矩阵(6)可以看出，编码后的信息块C产生了冗余，前6行还是原始数据，即数据块D，后3行为冗余数据，即校验块P。如果信息块C在存储过程中，有不超过3个子块失效，以子块D1、P2和P3失效为例，可将GD=C中对应的第1、8、9行删除得到：

(7)

(8)

即数据块得到了恢复。

由于RS编码中的G′使用了范德蒙矩阵，其特性决定了生成矩阵G中的G′在保证G删除任意的3行后得到的矩阵一定可逆。通过以上的例子可以发现，范德蒙矩阵在实践当中有着非常重要的应用。

3 结语

当授课教师在介绍一个数学概念时，有时需要说明概念的背景和用途；讲解一个定理时，有时要重点介绍证明的思路；而计算一个例子时，有时可以进一步探索它在实践中的应用。教师要认真梳理已有的知识点，找到其间的联系，并能够善于将一些重要的知识点进行拓展和串联，将基本的数学思想和方法传授给学生。同时，教师可以适当地在教学中介绍所讲授的知识在科研中的应用，分析科研思路，培养学生在学会做科研的同时，善于发现问题和提出问题。通过对前沿科研知识的介绍，可以尝试让学生探索一些具有研究性、探索性和开放性的问题，以案例教学、探究式教学或者是线上线下混合式等教学模式进一步展开教学活动。通过不断的训练，充分激发学生学习兴趣，更好地培养学生的创新精神、创新观念和创新能力。