三相感应电机定子端部漏感计算方法的对比分析

陈 磊,袁 德

(海装广州局，广东 广州 510320)

0 引 言

定子端部漏感是定子漏感参数的重要组成部分[1-2]，准确的端部漏感计算是电机过渡过程分析和高性能电机控制的关键[3]。目前计算电机定子端部漏感的方法已经较为成熟。

在传统电机设计中，一般采用经验公式计算端部漏感[4-5]。由于经验公式中含有大量简化使计算精度较低，当绕组端部形状不一样时需重新调整修正系数，给计算带来不便。文献[6]通过推导电机内电磁场方程计算端部漏感，但是电机内电磁场的推导较为复杂，当绕组端部形状复杂时难以求出相应的解析解。随着计算能力的提升，基于数值计算[7-15]的端部漏感计算方法得到广泛应用。文献[10]建立电机三维有限元模型，并基于能量法和端部磁链计算电机定子端部漏感，然而有限元三维建模繁琐且计算时间成本较大，不利于电机优化设计阶段；文献[11-13]采用基于Boit-Savart定理的离散积分法计算端部漏感，引入气隙电流和镜像电流等效气隙和铁心对端部漏磁场的影响，并将端部绕组分为若干小段，以每小段为数值计算单元，通过离散积分得到端部漏感；文献[14-15]采用基于矢量磁位的离散积分方法计算端部漏感，相比于基于Boit-Savart定理的计算法，基于矢量磁位的计算法不再受磁通面形状的影响，使绕组的空间建模更为灵活，且能考虑倾角和喇叭口等情况。

电机定子绕组端部类型较多，当采用不同的方法计算端部漏感时，由于方法本身存在差异导致计算误差也不同，需根据端部漏感计算方法特性以及绕组端部形状选择适用的计算方法，而目前还鲜有文献对不同端部漏感计算方法的适用范围进行研究。本文以喇叭口形、半椭圆形以及半矩形端部绕组为算例，采用能量法、Boit-Savart定理、矢量磁位的端部漏感计算方法对3种不同形状端部的漏感进行计算并将计算结果与试验测试结果进行比较，分析得出3种端部漏感计算方法的适用范围。

1 基于能量法的定子端部漏感计算

在三相感应电机中，端部漏磁场能量可以表示为

MendABIBIA+MendACICIA+MendBCICIB

(1)

式中：LendA、LendB、LendC分别为A相、B相、C相的绕组端部自感；MendAB、MendBC、MendCA分别为A相和B相、B相和C相、C相和A相的绕组端部互感；IA、IB、IC为三相电流幅值。

根据三相旋转感应电机的对称性有：

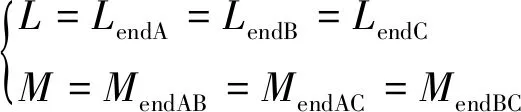
(2)

假设三相电流对称，那么可将式(1)进一步改写为

(3)

令L-M=Lend为某一相绕组的端部漏感，对式(3)进行变换可得端部漏感为

(4)

式中:Wend为电机端部磁场总能量；IA为绕组电流幅值。

端部磁场的总能量可利用Maxwell有限元仿真软件计算得出。在电机端部设置圆柱形求解域，如图1所示。求解域的磁场能量为

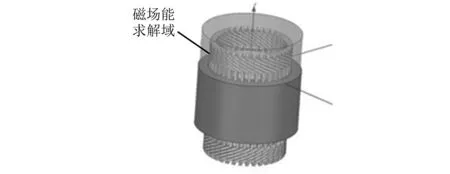
图1 端部磁场能量的求解域

(5)

通过Maxwell有限元仿真软件中场计算器对磁场能求解域内的能量进行积分即可得到端部磁场的总能量，再根据式(4)计算得到端部漏感。

2 基于Boit-Savart定理的定子端部漏感计算

2.1 绕组端部计算模型的建立

不同端部的绕组漏感计算模型如图2～图4所示。引入气隙电流和镜像电流将模型进行等效。为计及铁心内部线圈直线部分电流对端部磁场的影响，在定子槽中引入线圈直线部分电流的镜像电流。

图2 喇叭口形端部漏感的计算模型

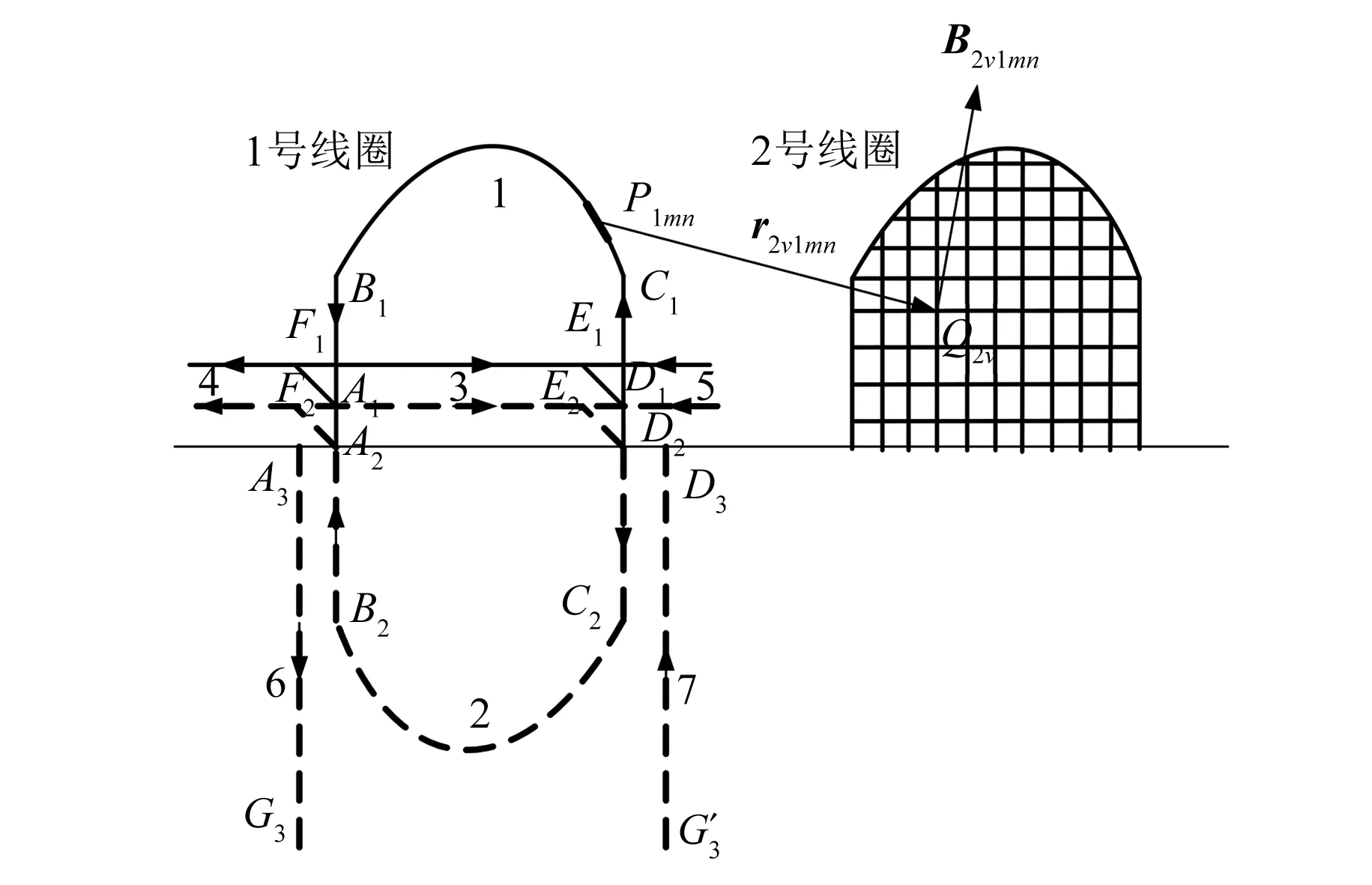
图3 半椭圆形端部漏感的计算模型

图4 半矩形端部漏感的计算模型

在图2～图4中，各绕组端部的计算模型可分为7大部分，其中第1部分为端部电流，第2部分为端部电流的镜像电流，第3～5部分为气隙电流，第6、7部分为定子槽内直线段镜像电流，其中各段电流的取值为

(6)

式中：i1m为1号线圈m段电流；N为线圈匝数；p为极对数；i为线圈电流幅值；β为短距比。

为增加端部漏感计算精度需充分考虑端部电流的空间分布。将绕组端部中各段电流分为若干小段，如将第m段电流分为n小段，每小段电流可用下标mn表示，并以每小段电流作为计算单元，采用Boit-Savart定理计算1号线圈每小段电流在2号线圈内产生的磁链。

在计算2号线圈内的磁链时，需选取2号线圈端部的磁通面并对其进行剖分，当绕组端部的磁通面形状较为复杂时会采用近似面来等效原磁通面。以喇叭口形端部为例，由于绕组为双层绕组，上层边和下层边不在同一圆内，为简化计算选取位于上层边和下层边之间的中层面进行磁通计算，如图5所示。

图5 喇叭口形线圈端部中层面

由于绕组圆弧部分存在倾角，半椭圆形端部绕组磁通面不在同一柱面内。为简化计算，对磁通面进行分块，如图6所示。磁通面1为平面矩形磁通面，磁通面2为平面半椭圆形磁通面。磁通面2的外轮廓与绕组圆弧段导体内表面重合。

图6 半椭圆形绕组端部的磁通面

由于半矩形绕组端部没有倾角，且绕组端部圆弧段的圆心与电机圆心相近，可建立如图7所示的磁通面。

图7 半矩形绕组端部的磁通面

2.2 各相端部漏感的计算

根据Biot-Savart定理，线圈1端部P1mn段在2号线圈Q2v点处产生的磁感应强度为

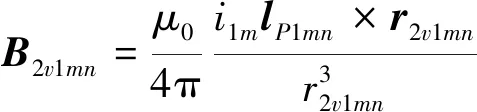
(7)

式中：μ0为空气磁导率；i1m为线圈端部m段的电流幅值；lP1mn为线圈端部P1mn段的长度矢量；r2v1mn为1号线圈P1mn段中点到点Q2v的距离矢量。

1号线圈P1mn段在2号线圈端部磁通面上产生的平均磁感应强度为

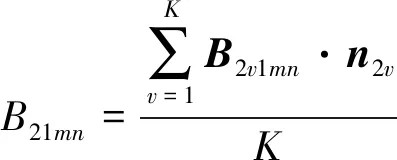
(8)

式中：K为2号线圈端部磁通面上所有的剖分点；n2v为Q2v点的单位法向量。

1号线圈与2号线圈的端部互感为

(9)

式中：S2为线圈2磁通面面积；Nm为m段电流的总数；Nn为每m大段电流所分段数。

在得到各个端部线圈的自感和互感后，需通过关联矩阵计算各相端部漏感。以18槽、1对极的三相感应电机为例，每个槽内均有上下2层线圈边，因此关联矩阵C的大小为6×18。其中矩阵每行分别对应A相绕组的上层边、A相绕组的下层边、B相绕组的上层边、B相绕组的下层边、C相绕组的上层边、C相绕组的下层边。把每槽线圈当成一条支路，每相绕组当成一个回路，并规定电流的正方向，再根据绕组连接关系，确定关联矩阵中各元素的值。当回路电流与支路电流相同时元素取值为1，相反时取值为-1，不相关时取值为0。

以电机的A相绕组为例，其绕组连接如图8所示，实线代表上层边，虚线代表下层边，采用短距的连接方式，并规定电流向上为正方向。

图8 A相绕组连接图

根据图8的连接方式以及电流正方向可以写出A相绕组的关联矩阵式(10)，其中矩阵的第一行对应A相绕组的上层边，第二行对应A相绕组的下层边；由于1号槽上层边电流方向为正，所以第一行第一列为1，矩阵中其他位置的参数同理。

(10)

得到各线圈之间的互感矩阵Mend和关联矩阵C后，各相端部漏感的计算公式为

(11)

式中：u和v的取值为1、2、3，且分别对应A、B、C相；Z为线圈总数；a为绕组并联支路数。

3 基于矢量磁位的定子端部漏感计算

3.1 绕组端部计算模型的建立

基于矢量磁位计算法的不同绕组端部漏感计算模型如图9～图11所示。利用镜像电流和气隙电流来等效铁心和气隙对端部磁场的影响，并将各段电流进行分段，分段方法以及各段电流取值与2.1节的方法相同，并确定各小段电流的空间坐标。

图9 喇叭口形端部漏感的计算模型

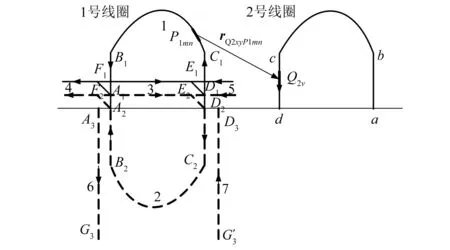
图10 半椭圆形端部漏感的计算模型

图11 半矩形端部漏感的计算模型

需确定2号线圈矢量磁位的积分路径。以喇叭口形绕组为例，图12所示为计算线圈端部磁通的积分路径，积分路径经过导体中心，再由端部h点以直线连接到另一端部a点，其中h点和a点为铁心端面与绕组的交点。2号线圈电流段的划分与1号线圈端部电流段的划分相似，分为8大段，分别为ab、bc、cd、de、ef、fg、gh、ha。最后将每段电流划分为n小段电流，并以每小段电流作为数值计算基本单元。

图12 绕组端部矢量磁位积分路径

基于矢量磁位的计算法不再受磁通面的限制，在沿线圈导体的一维空间上取点即可。但值得注意的是，在利用矢量磁位法计算绕组端部自感时，电流路径与积分路径重合，导致rQ2xyP1mn为0。根据式(13)，rQ2xyP1mn作为分母不能为0，因此需要重新选取积分路径。考虑绕组导体形状，选取导条内侧为新积分路径，图13所示为计算线圈端部自感的新积分路径。

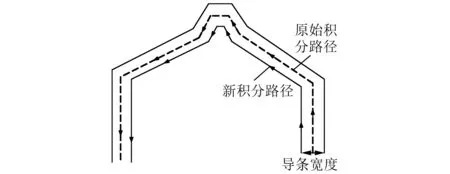
图13 计算线圈端部自感的新积分路径

3.2 各相端部漏感

电流在空间中任意一点产生的矢量磁位可由下式计算得出：

(12)

那么1号线圈P1mn段电流在2号线圈Q2xy段处产生的矢量磁位为

(13)

式中：lP1mn为1号线圈P1mn段处的长度矢量；rQ2xyP1mn为1号线圈P1mn段中点到2号线圈Q2xy段中点的空间距离。

根据式(13)，1号线圈电流在2号线圈Q2xy处产生的矢量磁位为

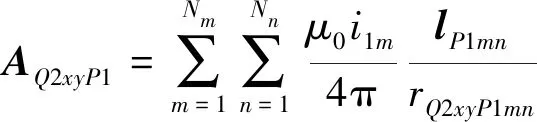
(14)

根据Stokes原理，矢量磁位A在任意闭合回路上的矢量积分等于闭合回路所包围曲面的磁通量，即

(15)

根据式(15)，将2号线圈上矢量磁位沿积分路径离散积分得到1号线圈电流在2号线圈端部产生的磁链为

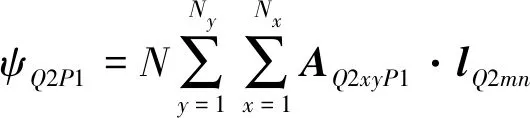
(16)

式中：Ny为2号线圈电流段的总数；Nx为每y段电流所分小段电流总数；lQ2mn为2号线圈Q2mn处的长度矢量。

根据磁链表达式式(16)，1、2号线圈端部漏感为

(17)

式中：i1为1号线圈的电流。

计算得到各线圈端部漏感后，通过关联矩阵和式(11)对各相漏感进行计算。

4 不同形状绕组端部漏感计算及试验验证

选取3台绕组端部形状分别为喇叭口形、半椭圆形以及半矩形的电机为试验对象，3台电机的端部绕组形状如图14所示。

图14 不同绕组端部形状的样机

试验所用喇叭口形端部绕组的电机为六相感应电机，为方便对比将1Y绕组和2Y绕组串联变为三相感应电机；半椭圆形端部绕组电机为普通的三相绕线型电机；半矩形端部绕组样机为大功率推进电机的缩比样机。

3台电机的基本参数以及绕组端部的形状参数如表1所示。

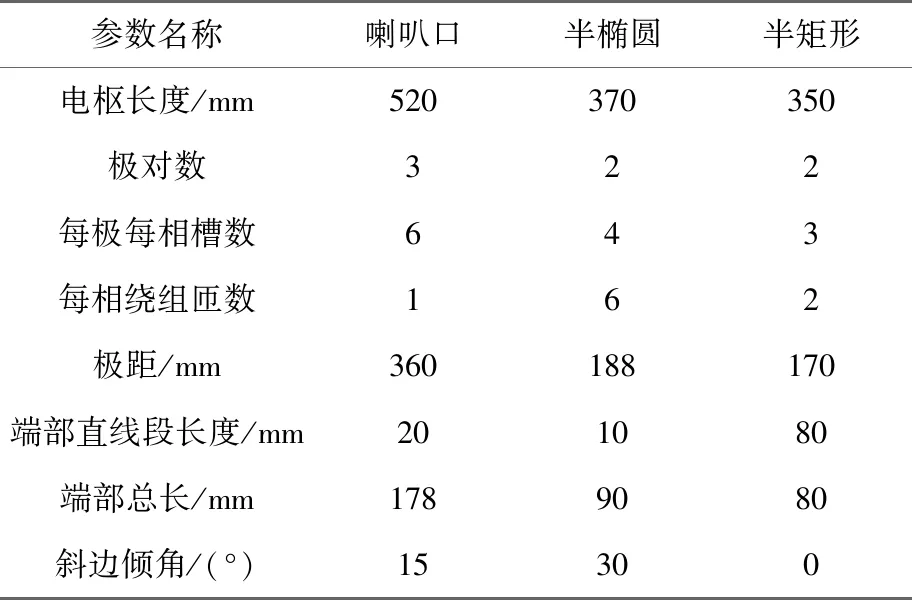
表1 电机基本参数

由于绕组端部漏感难以采用试验直接测量，参考文献[16]的方法对端部漏感进行测量。

分别利用能量法、基于Boit-Savart定理的计算法和基于矢量磁位的计算法对喇叭口形、半椭圆形以及半矩形端部绕组电机的端部漏感进行计算。计算及试验测量结果如表2所示。

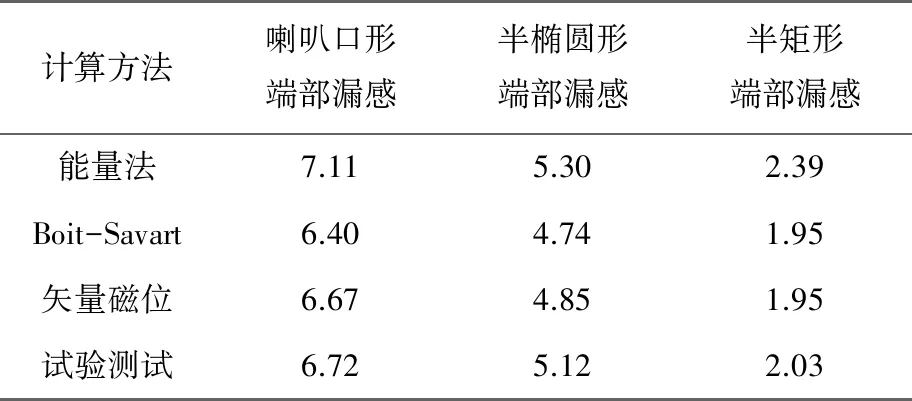
表2 端部漏感计算及试验测量结果 mH

对比表2的结果，可以看出：喇叭口形绕组端部漏感，采用矢量磁位计算的结果与试验测试结果最为接近；半椭圆形绕组端部漏感，采用能量法计算的结果与试验测试结果最为接近；半矩形绕组端部漏感，采用基于Boit-Savart定理的计算结果和矢量磁位的计算结果均与试验测试结果相近。

结合表2的对比结果以及3种端部漏感计算方法的特性，总结如下。

(1) 喇叭口形绕组端部漏感宜采用矢量磁位法计算。基于矢量磁位的计算法能够计及喇叭口处的磁通量和斜边部分倾角，计算精度较高且计算速率较快；能量法能够考虑到喇叭口处磁通量以及斜边倾角，但计算误差较大，其原因在于求解域内不仅有端部绕组产生的磁场，还有其他部件产生的漏磁；基于Boit-Savart定理的计算法需对绕组端部的磁通面进行剖分，如果磁通面的形状过于复杂会使建模难度增加，对于喇叭口形则是采用中层面进行简化，简化后无法计及喇叭口处磁通量以及斜边倾角，导致精度不及矢量磁位法。

(2) 半椭圆形绕组端部漏感的计算宜采用能量法。半椭圆形绕组的端部具有倾角且绕组端部的圆弧段不规则，其空间坐标及磁通面建模较为复杂，为方便计算在建模时会进行一定简化，使误差增大，因此基于Boit-Savart定理的计算法和基于矢量磁位的计算法不适用。

(3) 半矩形绕组端部漏感的计算宜采用基于Boit-Savart定理或基于矢量磁位的计算法。由于半矩形绕组端部结构较为简单，其圆弧段一般与电机同心，磁通面的建立以及绕组端部一维坐标的选取均比较容易，宜采用比能量法精度更高的Boit-Savart计算法或矢量磁位计算法。

5 结 语

本文以喇叭口形、半椭圆形以及半矩形端部绕组为例，采用能量法、Boit-Savart定理、矢量磁位的端部漏感计算方法对3种不同形状端部的漏感进行计算，并将计算结果与试验测试结果进行比较，分析得出3种端部漏感计算方法的适用范围。

总结得出，当绕组端部不存在倾角且磁通面外轮廓规则时，可利用Boit-Savart计算法或矢量磁位计算法；当绕组端部存在倾角且绕组端部一维坐标的选取均比较容易时，宜采用矢量磁位计算法；当绕组端部不规则，建模较为困难时，宜采用能量法。