对接圆柱壳结构模态特性分析*

李旭龙 张忠 魏莎,3† 丁虎,3 陈立群,3

(1.上海大学 力学与工程科学学院,上海 200444)(2. 北京强度环境研究所 可靠性与环境工程技术重点实验室，北京 100076)(3. 上海市应用数学和力学研究所，上海 200072)

引言

近年来，随着航空航天、船舶和机械等工程领域的迅速发展，柱壳结构得到了广泛应用.目前圆柱壳、球壳、加筋圆柱壳等[1, 2]结构的振动特性已有诸多相关研究工作，但对于工程中常见的对接圆柱壳结构振动特性的研究较少.对接圆柱壳结构是一种常见的简化对接结构.此类结构模态参数是对其结构动力学特性分析的基础，是新型航天飞行器等工程结构设计优化的重要参数之一.因此，分析对接圆柱壳结构的模态特性具有十分重要的意义.

为获取该类组合结构的模态特性，许多学者展开了研究.吴仕昊等[3]基于Reissner薄壳经典理论，采用区域分解法分析了圆锥壳-柱壳-壳组合结构在不同边界条件下的自由振动特性.张帅等[4]提出了一种改进傅立叶级数的半解析方法，分析比较了结构几何参数变化对锥柱球组合壳自由振动的影响.但由于理论分析所得结果多为近似值，日益复杂的组合几何构型较难满足精度要求；有限元仿真分析则由于结构阻尼、连接刚度等参数较难确定，计算结果的可靠性难以保证.

实验模态分析方法为上述问题提供了解决途径.王松松等[5]采用实验模态分析方法得到了不同折叠状态下Z形机翼的模态参数，为机翼结构设计提供了参考依据.焦标强等[6]基于PolyMAX模态参数识别法成功获取了轴装式制动盘的模态参数，为该类结构的结构优化设计建立了基础.王民等[7]结合实验测试和有限元仿真分析了机床主轴头的模态特性，提出增加背板可有效进行结构减震.

本文以对接圆柱壳结构为研究对象，基于ABAQUS有限元软件及LMS Test. Lab测试软件建立了有限元模型与实验模型，并分别进行计算与实验模态分析.实验模态分析过程中，针对自由边界的实验实现、分析结果的正确性进行了讨论，并将其与计算模态分析结果进行对比，验证了计算模态分析结果的正确性.通过上述分析过程得到的对接圆柱壳结构模态振型特征，可为工程领域中对接圆柱壳结构的动力学设计提供参考依据.

1 对接圆柱壳结构的模态分析原理

模态分析利用耦合物理坐标系统与无耦合模态坐标系统之间的转化关系，建立系统物理参数与模态参数之间的数学关系，通过测量结构的频响函数以获取振动系统的模态参数.根据材料结构特性和振动理论，对接圆柱壳结构可采用多自由度系统进行描述，其动力学微分方程可描述为[8, 9]

(1)

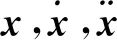
本文主要分析对接圆柱壳结构的固有特性，方程(1)的特征方程为

K+iωC-ω2M=0

(2)

其中ω为特征频率.

通过求解方程(2)即可得到固有频率(特征值)以及振型(对应的特征向量).同时，可将方程(1)进行拉普拉斯变换，通过变量变换将方程从时域转换到频域，方程形式如下

(Ms2+Cs+K)X(s)=F(s)

(3)

式(3)可简写如下

Z(s)X(s)=F(s)

(4)

其中Z(s)为系统在s域上的阻抗矩阵，则系统的传递函数矩阵可表示为

(5)

其中adjZ(s)和detZ(s)分别为Z的伴随矩阵和行列式.将式(5)按照极点展开

(6)

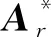
2 PolyMAX方法的基本原理

比利时LMS公司基于最小二乘复指数方法开发了一种全新的频域分析方法，改进了最小二乘复指数方法在处理模态密集且频率较高系统时易产生虚假模态、极点稳态图混乱、模态定阶困难等不足.这种模态参数辨识方法即为PolyMAX方法，也称最小二乘复频域方法(Polyreference Least-Squares Complex Frequency-domain Method)[10]，它采用SVD方法避免了留数的分解，使得密集空间分离且在强阻尼、模态密集情况下仍具有较好的实用性，结果的客观性更好.

实测得到的频响函数模型可表达如下

(7)

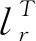
采用最小二乘复频域法求解模态振型时，其极点-留数模型的拟合函数为

(8)

其中，φr为模态振型;LR和UR分别为上下残余项;*为复共轭矩阵.

3 对接圆柱壳结构的计算模态分析

3.1 对接圆柱壳结构有限元建模

本节基于ABAQUS有限元软件对对接圆柱壳结构模型进行了有限元建模、网格划分以及动力学特性分析.已知对接圆柱壳结构整体采用6061铝合金进行加工制作，密度为27500 kg/m3，弹性模量为71 Gpa，泊松比为0.33，所采用的边界条件为自由边界.图1为对接圆柱壳结构示意图，基本参数如表1所示.

表1 对接圆柱壳结构基本参数

图1 对接圆柱壳结构示意图

有限元分析过程中，网格及单元设置的合理性对于分析结果的准确性影响最大且最为直接.为准确表征对接圆柱壳结构的连接形式，于螺栓孔中心处建立节点并用MPC约束将其与孔周的节点连接起来，随后采用RBE2单元进行螺栓的模拟.在对对接圆柱壳结构进行网格划分时，法兰盘部分采用八结点线性六面体单元进行扫略生成，筒壁部分采用四节点四面体单元自适应生成，共计18060个单元，建立的模型网格如图2所示.

图2 对接圆柱壳结构有限元模型

3.2 计算模态分析结果

通过对对接圆柱壳结构进行计算模态分析，可得到结构的各阶固有频率和模态振型，如图3所示.

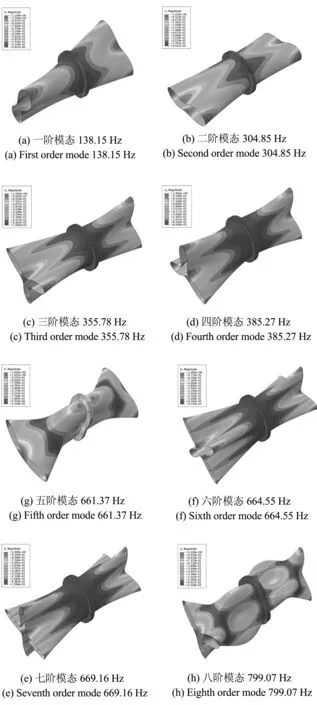
图3 前8阶有限元模态分析结果

从图中可以发现对接圆柱壳结构周向半波数和轴向波数随着模态阶数的增加而呈增加趋势，表现为圆柱壳结构的一般振动特性.同时，由于结构为螺栓对接形式，部分阶模态振型呈现出以法兰面为分界的非对称振动，该振动特性可为结构工程领域的动力学设计提供参考依据.

4 对接圆柱壳结构的实验模态分析

4.1 实验方案

为验证有限元模型及模态分析结果的正确性，本节对对接圆柱壳结构进行实验模态分析.实验过程采用单点激励多点响应形式，利用冲击力锤施加脉冲激励，通过力传感器信号和拾振点处的三轴加速度传感器信号反馈给数据采集系统，结合输入和输出信号进行曲线拟合，从而识别系统模态参数.

在实验模态测试过程中，所用到的仪器设备包括:LMS Sadas Mobile(SCM04)多通道数据采集器、B&K三轴加速度传感器(Type:4529-B-001)、B&K 8206-002 型冲击锤和LMS Test. Lab数据采集分析系统，实验模态测试系统如图4所示.

图4 实验模态测试系统示意图

为准确描述试验件的几何特征，本节在LMS Test. Lab软件中的Geometry模块建立了一个由多个测点组成的结构模型.对于整体结构将其沿周向进行8等分，其中圆柱壳部分按照实际尺寸沿轴向进行了10等分(间隔10cm)并将等分点设为测点，法兰盘部分则根据实际尺寸在特征点进行测点的设置，共划分112个测点.拾振点的选取应避开关注模态的节点位置以得到完整的各阶模态结果，实际共布置拾振点8个，采取非对称的布置方式.图5为对接圆柱壳结构拾振点位置示意图.

图5 对接圆柱壳结构拾振点位置

4.2 边界条件的实验实现

约束边界往往需特制夹具进行实现且夹具的优劣会对结构的模态特性产生较大的影响.基于此，试验过程中采用自由边界进行模态测试.目前模拟自由边界的方式主要有：弹性绳悬挂、海绵垫支撑、橡胶垫支撑等，本文根据试验件几何结构的特殊性，采用了弹性绳悬挂的方式.同时，为避免边界条件对测试结果的影响，进行了多种悬挂方式的探讨，如图6所示.

图6 试验件的悬挂方式

通过上述多角度的比较与分析，可得出以下两点结论：(1)非贯穿悬挂方式较大地影响了激励-响应过程，从而使得部分频率响应函数在模态较为密集处出现混乱；(2)针对对接圆柱壳结构，若需获取较高质量频响函数，贯穿悬挂方式更利于数据采集与分析.

表2为不同悬挂方式下固有频率的对比结果，其绝对差值最小为0.13 Hz、最大为2.12 Hz，相对误差最小为0.04%、最大为0.67%.结果表明不同悬挂方式对于模态测试结果的影响较小，两组结果中固有频率吻合度较高.为进一步探讨悬挂方式的具体影响，本文分析比较了不同悬挂方式下利用PolyMAX方法计算得到的极点稳态图，以模态较为密集的频段600～700 Hz、850～950 Hz为例，如图7所示.通过对比密集频段处的极点稳态图可知，贯穿悬挂方式能够得到一系列稳定的物理极点从而获取真实的模态参数信息，而非贯穿悬挂方式在SUM曲线(频响函数的集总函数曲线)的峰值频率处易出现“v”点，即不稳定点.

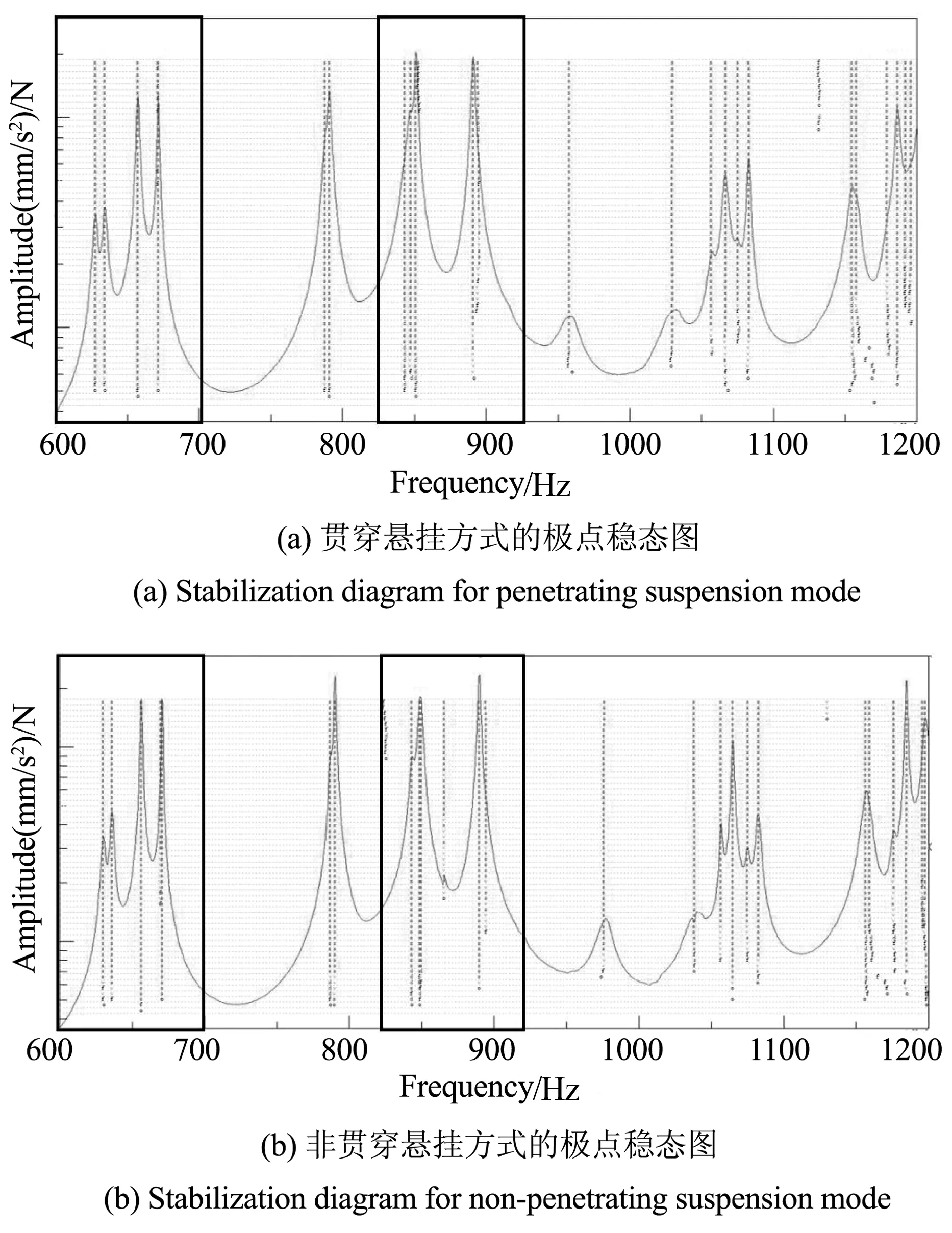
图7 不同悬挂方式下极点稳态图

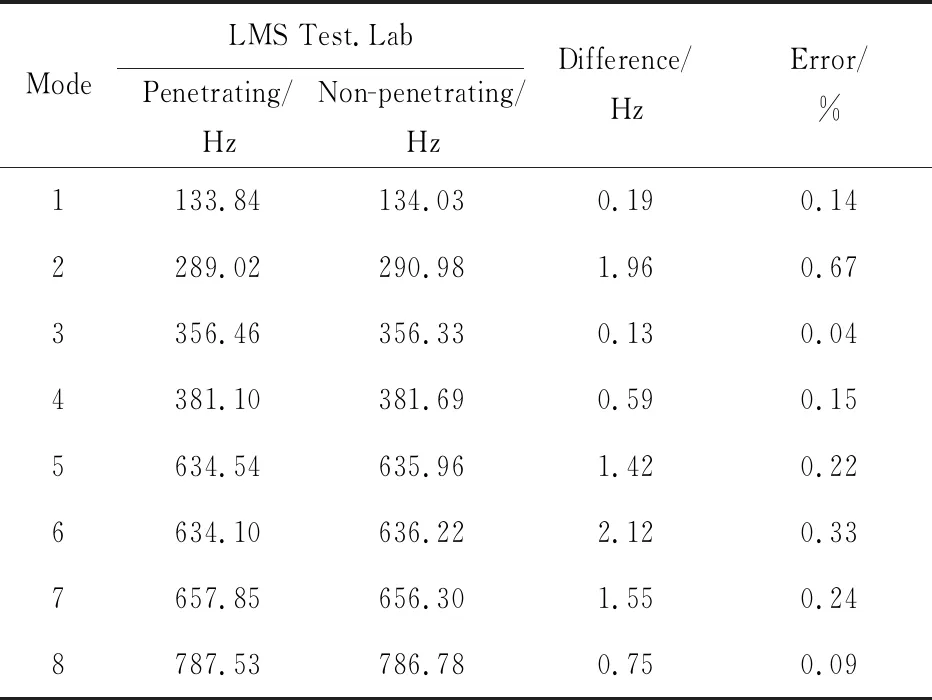
表2 不同悬挂方式下系统的固有频率

4.3 实验模态分析结果及对比

基于上述研究，本文采用贯穿悬挂方式对对接圆柱壳结构自由边界进行模拟，并沿用上述实验过程进行模态测试实验.实验中，依次对112个测点进行径向激励并对对应的频率响应函数进行5次有效值平均，计算得到前8阶固有频率及阻尼比.表3为对接圆柱壳结构前8阶模态参数汇总，其中，m、n分别表示模态的轴向波数和周向半波数.

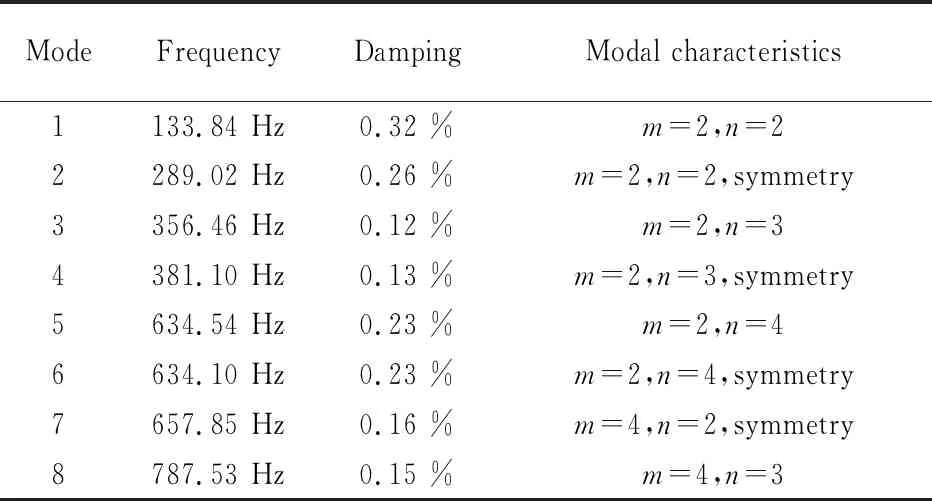
表3 对接圆柱壳结构前8阶模态参数

模态置信因子(MAC)是振型向量之间的点积，用以评价两个模态振型的相关性，可表示为

(9)

其中φi、φj为模态振型向量.MAC矩阵提供了一种模态相似度的评判依据，当模态置信度矩阵非对角线元素越小，各阶计算模态振型的独立性则越好，图8为此次实验模态测试的MAC值.从图中结果可以看出，MAC矩阵对角线上元素均接近于1，非对角线上元素均接近于0，各阶模态振型相互独立.MAC矩阵表明，实验模态测试结果准确可靠，基于PolyMAX模态参数识别方法能够有效识别复杂结构的模态参数.

图8 实验模态分析的MAC矩阵

根据模态振型一致原则，将实验模态分析结果与计算模态分析结果进行对比，如表4所示.通过表4可以发现，实验模态分析结果与计算模态分析结果具有较小的相对误差，其中最大相对误差为5.24%，满足精度要求.综上，实验模态测试结果验证了有限元建模及模态分析的正确性.

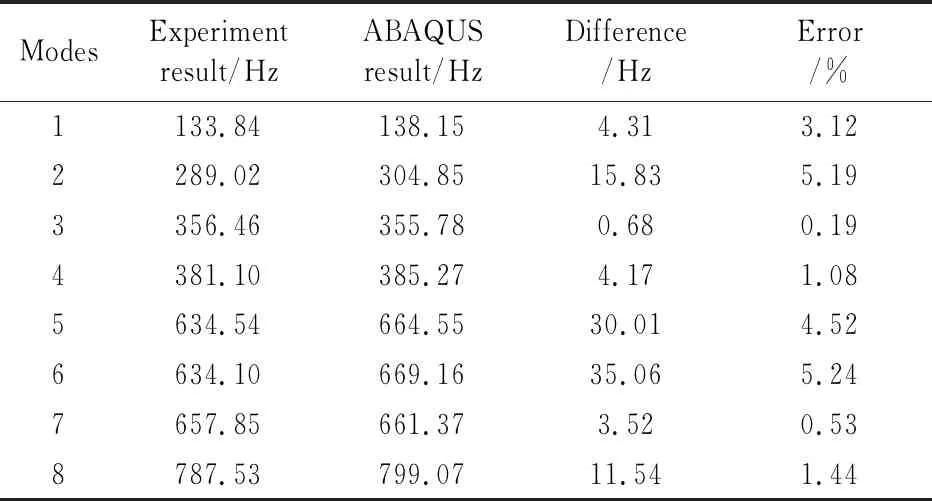
表4 实验模态结果与有限元结果对比

5 结论

本文采用ABAQUS有限元软件建立了对接圆柱壳结构有限元模型，并进行了计算模态分析.采用LMS数据采集分析系统进行了多种悬挂方式下的对接圆柱壳结构实验模态测试，并基于最小二乘复频域法进行了实验模态分析.通过上述模态分析过程及结果，可得以下结论：

(1)实验模态分析结果与计算模态分析结果具有较好的一致性，前者验证了有限元模型及模态分析结果的正确性，所建立模型可广泛运用于对接圆柱壳结构的模态振动分析.

(2)贯穿悬挂方式对于对接圆柱壳结构自由边界条件的实验实现更优.通过该种悬挂方式，可获取较高质量的频响函数，从而获取真实的模态振型及其他模态振动参数.

(3)通过对接圆柱壳结构模态振型的分类讨论，发现其周向的半波数和轴向波数随着频率的增加而呈增加趋势，表现为圆柱壳结构的一般振动特性.但由于结构为对接形式，模态振型呈现出以法兰面为分界的非对称振动，该特性可为结构工程领域的动力学设计提供参考依据.

(4)模态振型MAC矩阵表明，实验模态分析结果准确可靠，基于PolyMAX方法可准确识别模态参数.