多目标交会轨迹优化方法综述*

陈诗雨 宝音贺西

(清华大学 航天航空学院，北京 100084)

引言

在许多航天任务中，航天器需要对目标天体进行环绕、着陆或对目标航天器伴飞，使得航天器与目标相对于中心天体的位置、速度近似一致，这种情形统称为与目标交会.在深空探测中，航天器在单次任务中交会多个目标能获得更多的科学回报.然而与地心轨道相比，日心轨道速度较大，相应地，在深空中与目标交会需要更大的速度增量和更多的推进剂，这对航天器的变轨能力提出了极高的要求.因此，20世纪的深空探测任务大都采用飞越而非交会的形式，以利用有限的推进剂实现对多个目标的探测.例如，“旅行者”1号、2号探测器飞越探测了太阳系各个大行星，“伽利略”号探测器在前往木星的途中飞越了金星、小行星51 Gaspra和243 Ida[1].进入21世纪，电推进技术的兴起促进了多目标交会任务的实现.电推进具有推力小且作用时间长的特点，故又称为连续小推力.电推进发动机比冲通常比传统的化学推进发动机高一个数量级，因此能显著地节省燃料.得益于电推进技术， “黎明号”探测器先后对小行星Vesta和Ceres进行了绕飞，这也是目前唯一成功的多小行星交会任务[2].若将探测器返回地球并着陆视为与地球的一次交会，则采样返回任务也属于多目标交会任务.近年来频繁开展的小行星采样返回任务中，电推进技术亦被广泛地应用，例如“隼鸟”1号、2号小行星探测器[3,4]和我国将于2024年发射的小行星探测器[5]均采用电推进技术.可以预见，随着电推进或更先进的推进技术愈发成熟，未来的深空探测任务将越来越多地采用多目标交会的形式以获取更大的收益.

在近地空间在轨服务领域，包括空间碎片清除和在轨加注等，多目标交会也有广阔的应用前景.近地轨道空间碎片的持续增长正威胁未来空间活动的安全，因此空间碎片清除是近年来的一大研究热点.为了节省任务成本，应使一颗航天器清除尽可能多的目标碎片.目前已提出了几种单航天器清除多目标的解决方案，例如航天器依次捕获数个目标并将它们弹射使其降轨[6]，或分别在每个目标上附着一个降轨设备[7]等.这些方案都需要航天器依次交会各个目标碎片，本质上都是多目标交会任务.空间碎片清除目前尚停留在理论研究阶段，而在轨加注已有工程应用经验.2007年，美国的“轨道快车”任务成功实施，验证了自主交会对接、在轨加注等在轨服务的关键技术.在该任务的应用场景中，服务航天器利用其自身的燃料或者从近地停泊轨道的仓库内获取燃料，与目标航天器依次交会并对其进行服务，是典型的多目标交会任务[8].

总之，在未来小行星探测、在轨服务等领域中将大量开展多目标交会任务，而轨迹优化是开展此类任务要解决的首要问题.多目标交会轨迹优化问题中优化变量众多，其中既有交会时刻等连续变量，也有交会目标等离散变量，且涉及的约束复杂，求解极其困难，因此是航天动力学领域的研究热点之一.国际空间轨道设计大赛(Global Trajectory Optimization Competition, GTOC)为多目标交会轨迹优化的研究起了重要的推动作用.该赛事由欧洲航天局先进概念组的Dario Izzo博士发起，每一到两年举办一届，参赛队伍来自各国的航天机构和高校，可谓国际航天动力学领域一大盛会.每届GTOC主办方都会提出一个解空间极大的轨迹优化问题，各参赛队伍在不到一个月的时间内提交结果，由当届冠军主办下一届比赛.迄今为止，GTOC已举办了10届，表1中列出了其中5届比赛中提出的多目标交会问题，涵盖了多小行星探测、空间碎片清除等任务[9].部分问题涉及多航天器协同的任务规划，进一步增大了解空间，难以找到全局最优解.在求解此类问题时，往往将原本复杂的离散-连续混合变量优化问题分解为全局优化和局部优化两部分[9].所谓全局优化指搜索最优的交会目标、序列及时刻，是一个包含连续变量的组合优化问题；局部优化指交会序列确定后，对每段目标-目标转移轨迹单独进行优化或对多段转移轨迹进行整体优化.

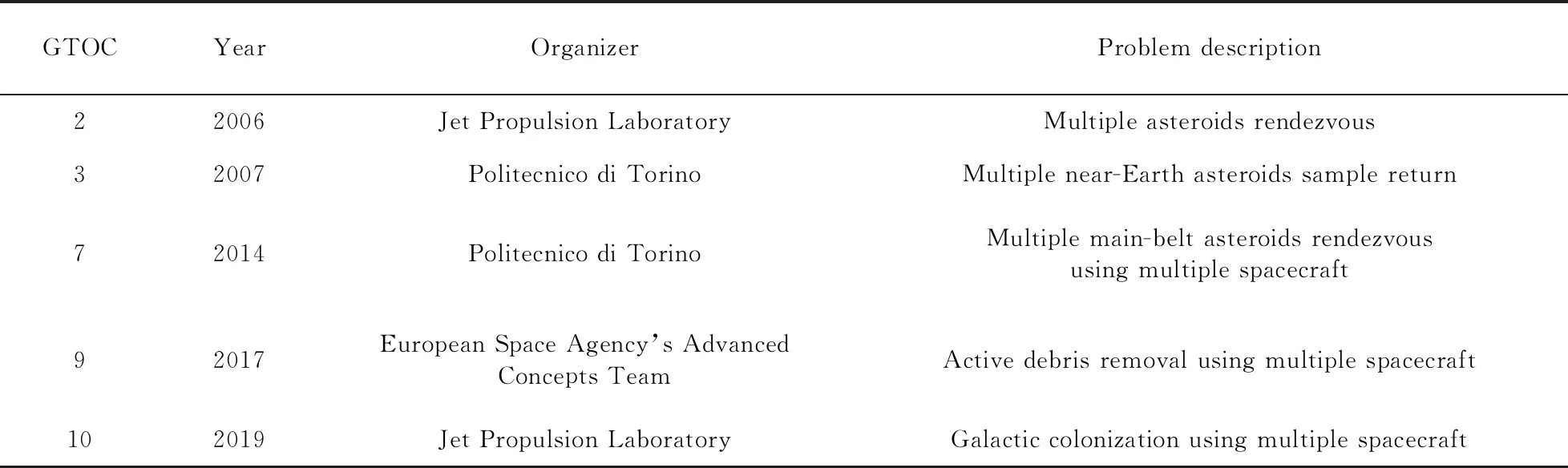
表1 GTOC中的多目标交会问题

在优化交会序列时需不断计算相应的优化指标，而指标和每段转移消耗的速度增量或时间等相关.对于动力学模型较简单的情况，例如二体模型下的脉冲转移，可直接在序列搜索的外层循环中调用局部优化算法求解每段转移的最优轨迹及其代价[10,11].然而当动力学模型较复杂时，例如考虑J2摄动或航天器采用连续小推力，仅优化单段转移轨迹就需耗费较多计算时间，在序列搜索时反复调用轨迹优化算法的计算代价难以接受.因此需简化模型，快速地估计转移消耗的最优代价.

综上，多目标交会轨迹的优化问题可分为三个子问题：转移代价估计、交会序列优化和转移轨迹优化.三者的关系：对转移轨迹优化中的模型简化后得到转移代价估计方法；估计的转移代价在交会序列优化中用于计算指标；对于优化后的交会序列，再精细地优化各段目标-目标转移轨迹.前人针对这三个子问题已做了大量研究，本文对这些研究工作进行总结.

1 转移代价估计方法

为提高序列优化的计算效率，转移代价估计的计算耗时必须短.同时，估计的转移代价决定了交会序列指标的评估，进而影响最优序列的选取.因此估计结果应尽可能接近轨迹优化的结果，以期能准确地评估序列的指标.常用的估计方法可分为数据库法、机器学习法和解析法三类.

1.1 数据库法

数据库法的思路：首先离线生成一个数据库储存所有可行转移的信息，每个可行转移的代价由轨迹优化算法给出，在序列优化中通过在线查询数据库得到所需的转移代价.从而避免了在线进行复杂的轨迹优化计算，同时又能保证估计的转移代价与优化结果之间误差较小.Cerf[12]在生成数据库时将转移的初始时刻和转移时间在一定区间内离散，并通过线性插值得到给定转移的速度增量，时间离散步长越小，数据库包含的可行转移越多，插值估计的速度增量也越准确.Bang和Ahn[13,14]、Petrov和Noomen[15]将数据库中的转移拼接成可行的交会序列，搜索空间的大小由数据库中包含的可行转移的数量决定.可见，数据库中可行转移的数量越多，最终的优化效果越好，但生成数据库消耗的计算时间也越长.文献[12]中生成40320个可行转移耗时112 h，文献[14]中生成23926个可行转移耗时37 h.在第9届GTOC中，冠军JPL生成了包含2.9×108个转移的数据库[16]，这对硬件的计算能力和内存提出了极高的要求.

1.2 机器学习法

近年来一些学者尝试将机器学习方法应用于转移代价的估计.首先使用局部优化算法优化大量转移轨迹，生成数据集，然后利用数据集训练神经网络，最后用训练好的神经网络估计转移代价.Hennes等[17]和Mereta等[18]使用机器学习估计近地小行星间小推力转移的航天器剩余质量，估计精度显著高于Lambert转移近似.Zhu和Luo[19,20]、Li等[21]使用机器学习估计了小行星间小推力转移以及空间碎片间多脉冲转移的速度增量，估计结果的平均相对误差分别约为0.5%和4%.Song和Gong[22]研究了太阳帆航天器交会多个小行星的场景，使用机器学习估计了最短转移时间.采用机器学习方法估计转移代价，只需生成包含上万个转移样本的数据集即可得到较高的估计精度，但生成数据集并训练神经网络仍需耗费数十小时.而且如果神经网络的应用场景与训练时的场景不同，则估计精度可能大幅下降，需重新生成数据集进行训练.

1.3 解析法

要节省离线生成数据库或数据集的时间，并使得转移代价估计方法适用于不同但相似的场景，较为传统的思路是对该类场景的转移轨迹进行解析近似.早在1961年，Edelbaum[23]就已针对近圆轨道的多圈转移场景(假设半长轴、倾角改变量很小)，推导了脉冲和连续小推力转移的速度增量估计公式.Alfano和Thorne[24]针对共面圆轨道间的连续推力转移，给出了最短转移时间的解析估计方法.Kechichian[25]基于Edelbaum的方法和最优控制理论推导了非共面圆轨道间小推力转移的最短转移时间估计公式.Kluever[26]在Kechichian工作的基础上考虑了地球阴影区的影响.Casalino和Colasurdo[27]对Edelbaum的小推力速度增量估计方法做了改进，考虑了推力方向和大小的最优控制，并推广到推力大小和比冲可变的情况.针对一圈以内的共面近圆轨道小推力转移轨迹，Casalino[28]基于Edelbaum的方法提出了最优速度增量半解析估计方法，相对误差不超过10%.Gatto[29]将Casalino的工作推广到了非共面转移的情形.Li等[30]在Edelbaum的小推力速度增量估计公式的基础上考虑了J2摄动，引入升交点赤经漂移带来的速度增量.Shen[31]推导了J2摄动下圆轨道间的小推力速度增量估计公式，考虑了开机-滑行-开机三段式转移，估计结果的相对误差仅为4%.此外，还有学者应用基于形状的方法，将连续推力交会轨迹近似为指数正弦或逆多项式曲线，解析计算速度增量[32-34].可见，许多学者研究了小推力交会轨迹的速度增量估计方法.对于脉冲转移，尤其是考虑J2摄动的速度增量估计，目前研究较少.Shen等[35]和Li等[36]利用升交点赤经的自然漂移，选择航天器与目标升交点赤经之差最小的时刻作为交会时刻，应用Edelbaum的公式估计调整轨道半长轴、偏心率、倾角所需的脉冲大小.Luo等[37]基于Gauss变分方程给出了调整轨道半长轴、偏心率、倾角、升交点赤经所需的速度增量估计公式.但这些脉冲速度增量估计方法的平均相对误差都在20%左右[20]，精度较差.Shen和Casalino[38]提出一种解析估计方法，考虑了升交点赤经漂移率的调整，充分利用轨道面进动来降低速度增量，使得估计的最优速度增量更接近实际值，平均相对误差低于10%.Chen和Baoyin[39]提出了一种解析估计方法，将脉冲转移速度增量的求解近似为求解一系列线性方程组，仿真结果表明此方法得到的速度增量估计值平均相对误差低于4%.Riggi和D’Amico[40]、Huang等[41]提出了半解析的脉冲转移速度增量估计方法，能达到更高的估计精度，但都需要迭代求解非线性方程，计算量远大于解析法.总之，目前解析或半解析的速度增量估计方法很难兼顾估计精度和计算效率.

1.4 小结

上述三类转移代价估计方法中，数据库法和机器学习法适用的范围较广，只要能生成精确转移的数据库就能应用这两类方法，而精确转移轨迹的数值求解方法已经相对比较成熟.解析法需要对精确转移轨迹进行解析近似，针对不同的转移模型需要推导不同的解析近似公式，因此适用范围较窄.从计算效率上看，数据库法和机器学习法在线估计转移代价时具有较高的计算效率，但事先离线生成数据库需耗费大量时间，且应用场景发生变化时需重新生成数据库；解析法无须生成数据库，其在线估计转移代价的计算效率取决于计算过程的复杂程度.从估计结果的精度上看，数据库法和机器学习法通常能获得较高的精度；解析法的估计精度取决于解析近似模型与精确模型的相近程度，两者越相近则精度越高，但计算效率会随之下降.由此可见，针对复杂转移模型，例如在考虑J2摄动等摄动力的情况下，如何提高解析法的估计精度同时保证较高的计算效率是值得研究的方向.

2 交会序列优化方法

多目标交会序列优化是一个包含离散-连续混合变量的优化问题．离散变量包括目标的选取、交会顺序，连续变量主要为交会每个目标的时刻或每段目标-目标转移的时间等.由于交会、飞越、引力辅助等不同探测形式的序列优化问题本质上相同，因此本文将相关的研究一并总结.无论是深空中多天体探测的序列优化，还是近地轨道多空间碎片清除，或是多目标在轨加注的序列优化，所使用的优化方法都是相通的，主要可分为树搜索算法和随机启发式算法两类.

2.1 树搜索算法

树搜索算法从根节点开始，选择当前可交会的目标作为下一级节点，形成搜索树的一个分支.逐级扩展搜索树分支，直到无可交会的目标时搜索结束，从而得到一条交会序列.树搜索算法通常包括深度优先和广度优先两种策略，其原理如图1所示.深度优先策略着重于快速生成可行序列，搜索树的每一级都选择最优节点向下扩展直到搜索结束，然后向上回溯搜索其他分支；广度优先策略在搜索树的每一级穷尽所有可行的分支，本质上属于穷举算法.Barbee等[57]采用深度优先策略，提出了一种最邻近序列搜索方法，在离散的时间网格内搜索最优转移窗口，并选择速度增量最小的目标进行转移，此方法被成功应用于第4届GTOC的多小行星飞越问题[57]和多碎片清除问题[67]的求解.Braun等[68]用广度优先策略求解了多碎片清除问题，从15个最有价值的碎片中穷举4到5个目标组成的交会序列.

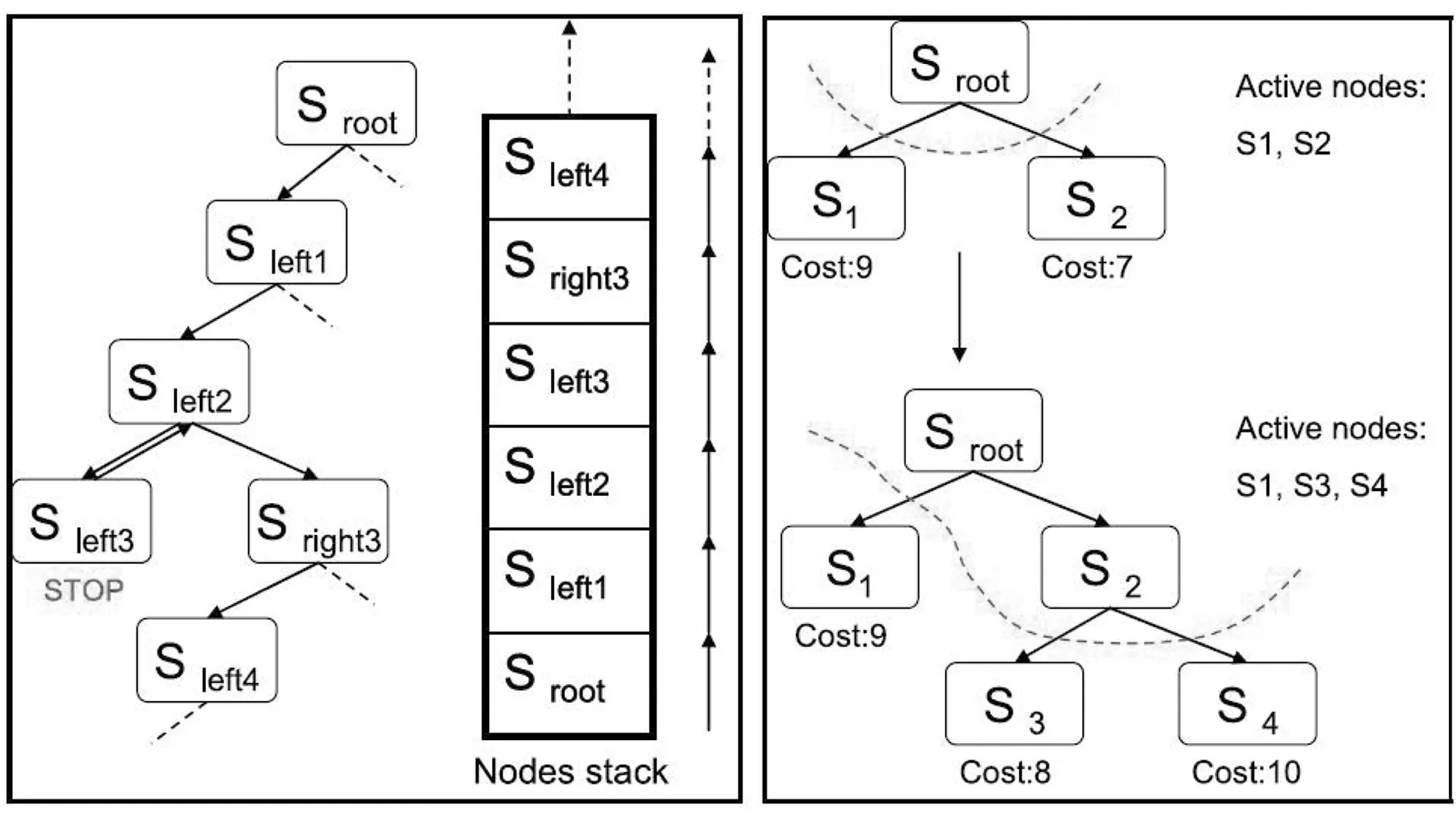
图1 树搜索算法示意图(左：深度优先，右：广度优先)[69]

上述两种搜索策略存在各自的局限性：深度优先策略的搜索空间小，极可能遗漏最优解；广度优先策略搜索空间大，但受限于计算资源，当交会目标过多时，无法穷尽所有分支.因此大多数情况下，采用树搜索算法时会用一种折中的策略：扩展搜索树的每一级分支前对该级所有可选分支进行评估，仅挑选其中一部分分支向下扩展.集束搜索法和分支定界法即采用这一搜索策略，其被广泛应用于多天体探测和多碎片清除序列的搜索中.Izzo等[51]基于集束搜索，提出了一种懒人树搜索算法，使用该算法求解第6届GTOC中的伽利略卫星借力序列优化问题，得到了比当届冠军更好的结果.Izzo等[61]还研究了第7届GTOC中的主带小行星交会问题，提出了一种多目标集束搜索算法优化交会序列.Di Carlo等[63]将分支定界法与差分进化算法结合，优化了主带小行星交会序列和交会时刻.Peloni等[65]使用了分支定界法优化了太阳帆航天器的多小行星交会序列.Cerf[69]研究了从11个碎片中清除5个的问题，使用分支定界法搜索了交会序列.Casalino和Pastrone[70]、Olympio和Frouvelle[71]从大量碎片中选出4到5个进行清除，同样使用分支定界法搜索了交会序列.Li等[30]、Barea等[75]分别采用集束搜索和分支定界算法求解了类似的问题.Madakat等[78]分别采用多智能体协同搜索算法和分支定界法对5个碎片的交会序列进行了优化.Bérend和Olive[84]采用双层优化思路，顶层使用分支定界法求解时变旅行商问题，底层优化多脉冲交会轨迹.

集束搜索法和分支定界法都是确定性的树搜索算法，即根据其剪枝策略保留的每一级分支是确定的，从而最终的搜索结果也是确定的，因此可能遗漏最优解.一种改进的思路是在选择每一级的分支时加入随机因素，从而增大搜索空间.具有代表性的是集束蚁群算法，该算法将蚁群算法中的信息素引入集束搜索中，使得较优的分支在剪枝时有更大的概率被保留下来，同时也不排除保留其他分支的可能性.Simões等[60]使用集束蚁群算法，研究了第5届GTOC中的小行星探测序列优化问题，得到了比确定性集束搜索更优的结果.Li和Baoyin[62]参考集束蚁群算法，提出一种集束进化精英算法，引入精英群体指导信息素的更新，进一步提升了集束搜索的性能.此外，蒙特卡洛树搜索也是一种典型的引入随机性的树搜索算法.Hennes和Izzo[52]使用蒙特卡洛树搜索研究多天体借力问题，得到了“卡西尼-惠更斯”号的借力序列.Fan等[64]研究了小推力多目标交会问题，用傅里叶级数近似小推力转移轨迹，并用蒙特卡洛树搜索优化交会序列.Song和Gong[22]使用蒙特卡洛树搜索优化了太阳帆航天器的多小行星交会序列.

2.2 随机启发式算法

随机启发式算法由于其随机特性，相对于确定性的算法具有更好的全局寻优能力.目前应用于序列优化的随机启发式算法主要有两类：进化类算法和群智能算法.

进化类算法受生物进化的原理启发，将一组可行解抽象为一个种群，通过染色体交叉、变异等机制改变种群个体的适应度，然后淘汰适应度较差的个体，从而使得种群得到进化.此类算法主要包括遗传算法、查分进化算法等.Vavrina[42]研究了多行星借力的小推力轨迹优化问题，首次将遗传算法作为外层循环搜索借力序列.Gad和Abdelkhalik[45]提出一种隐藏基因遗传算法，可在优化借力序列的同时优化借力次数，进而提出种群大小可变的遗传算法[46]，可同时优化借力次数、借力序列、深空机动次数以及发射时刻、到达时刻等连续变量.Darani和Abdelkhalik[47]对隐藏基因遗传算法做了改进，引入等位基因概念并提出了新的进化机制.Englander等[48]同样使用遗传算法优化脉冲轨迹的借力序列，引入空值基因实现优化借力次数的效果，之后又将此方法应用于小推力轨迹的借力序列优化中[49].Napier等[11]应用非支配排序遗传算法(NSGA-Ⅱ)同时优化了多个航天器的借力序列.Morimoto等[55]提出开展多近地小行星交会或飞越的采样返回任务，并使用遗传算法优化了小行星的探测序列和探测时刻.Conway等[56]将遗传算法和分支定界结合，求解了从8颗目标小行星中选择3颗进行飞越的序列优化问题，分别使用了遗传算法结合非线性规划(nonlinear programming, NLP)以及分支定界结合遗传算法两种优化框架对任务进行了优化.Zhang等[58]在混合编码遗传算法的基础上增强了对连续变量的搜索能力，在多小行星交会序列优化问题中该算法的结果优于双层遗传算法.在多碎片清除问题中，Murakami和Hokamoto[66]研究了从5个碎片中清除3个的问题，使用遗传算法优化了目标选择和交会序列.Liu等[73]研究了多目标优化问题，使用遗传算法优化碎片交会序列，使得清除的碎片面积最大，同时消耗的速度增量最小.Li等[76]提出了进化精英算法用于优化碎片清除序列，并进一步提出了混合进化精英算法，可同时优化连续变量.Izzo等[81]提出了带逆转算子的遗传算法，用于求解多碎片清除的旅行商问题，并与最邻近搜索、树搜索算法做了对比.Federici等[83]将碎片清除抽象为时变旅行商问题，将时间等连续变量离散化，如图2所示，然后用遗传算法和差分进化算法优化交会序列和交会时刻.针对多目标在轨加注问题，Zhang等[87]使用混合编码遗传算法优化了考虑时间窗口约束的多目标在轨加注序列.都柄晓[88]提出了多岛遗传算法，求解了基于合作交会的在轨加注序列优化问题.Zhu等[90]将聚类算法与遗传算法结合，优化了多目标在轨加注的交会序列.

图2 离散时间下5目标交会序列示例[83]

群智能算法受生物群体行为的启发，利用群体中个体的经验指导群体行为，最终使群体行为逐渐收敛到最优解上.此类算法主要包括蚁群算法、粒子群算法等.Stuart等[59]使用蚁群算法优化特洛伊小行星探测序列，提出将时间域离散，并行更新时间域上相邻转移对应的信息素.针对多天体借力问题，华鹏[44]使用粒子群算法优化了发射窗口和借力序列.Ceriotti和Vasile[43]将蚁群算法的信息素机制引入到序列搜索中，得到了比遗传算法更优的结果.Vasile等[50]提出了一种类似于蚁群算法的绒泡菌算法优化借力序列，该算法只需调试少量的参数即可达到优异的性能.在多碎片清除问题中，Di Carlo等[72]研究了两种碎片清除方案，在碎片集合中选取尽可能多的碎片进行清除，使用绒泡菌算法优化交会序列.Zhang等[74]在蚁群算法中引入2-优化、嵌入、交换三种局部搜索操作，使用该算法从碎片云中清除多个目标并优化了交会序列，使得清除的碎片面积最大.Shen等[35]使用蚁群算法从155个碎片中清除4个，优化交会序列使得航天器燃料消耗最小.Zuiani和Vasile[77]采用多智能体协同搜索算法对5颗碎片的交会序列进行了优化.Jing等[79]、Stuart[80]等分别使用多目标粒子群算法和蚁群算法对多航天器清除多颗碎片的交会序列进行了优化.在第9届GTOC中，主办方提出了多航天器清除123个太阳同步轨道碎片的问题，要求发射尽可能少的航天器、以最少的燃料清除所有目标[85].该届竞赛的前三名均使用了蚁群算法优化碎片清除序列[16,37,86].针对在轨加注问题，Zhang等[91]、Li和Xu[92]使用蚁群算法优化多航天器多目标在轨加注的交会序列.欧阳琦等[93]使用多目标粒子群算法求解了相似的问题.

除了上述两类算法外，其他智能优化算法如模拟退火算法[12,82,89]、列生成算法[14]等也被应用于多碎片清除和多目标在轨加注等交会序列优化问题中.

2.3 小结

本节概述了交会序列优化问题中使用的树搜索算法和随机启发式算法.树搜索算法中较常用的是集束搜索法和分支定界法，两者均为确定性的算法，搜索空间较小，往往会遗漏最优解.在确定性树搜索算法中引入随机因素，例如集束蚁群算法、集束进化精英算法等，可有效增大算法的搜索空间，提高其全局寻优能力.然而，目前的树搜索算法只能优化交会序列，缺乏对交会时刻等连续变量的优化能力.随机启发式算法中较常用的是遗传算法和蚁群算法.在求解离散-连续混合变量优化问题时，遗传算法可通过引入混合编码、隐藏基因等方式实现对连续变量的优化；而蚁群算法对连续变量的优化能力较弱，一般需要将时间等连续变量离散后转化为组合优化问题进行求解.因此，未来需进一步改进树搜索算法和蚁群算法，使其在搜索交会序列的同时能对交会时刻等连续变量进行优化.

3 转移轨迹优化方法

确定交会序列后需对航天器依次交会各目标的轨迹进行优化，指标通常为燃料消耗或转移时间.若将每段转移轨迹分别进行优化，前人已做了大量相关的研究.Shirazi等[94]对单段脉冲或小推力转移的轨迹优化方法做了详细、系统的总结，因此本节不再赘述，而是考虑对多段转移轨迹整体同时进行优化，总结相关的研究工作.

航天器的推进系统主要包括化学推进和电推进，其机动方式可分别抽象为脉冲和连续小推力，对应着不同的轨迹优化方法.脉冲机动可视为给航天器施加了瞬间的冲量，使其速度发生突变.优化脉冲转移轨迹时，通常以机动次数、施加脉冲的时刻、脉冲矢量的各分量作为优化变量，求解一个参数优化问题.而连续小推力持续施加在航天器上，其推力大小、方向随时间连续变化，相应的转移轨迹优化问题是典型的最优控制问题.

3.1 多段脉冲转移轨迹整体优化

Federici等[95]使用遗传算法优化了多段脉冲转移轨迹，但每段转移轨迹仅简单考虑为双脉冲转移，因此只需优化与各目标交会的时刻.关于多脉冲、多目标交会轨迹整体优化的研究较少，但许多学者研究了多次深空机动、多行星引力辅助的转移轨迹优化方法，差分进化算法[96-98]、粒子群算法[99-101]等算法在该问题的求解中展现出优异的性能.多脉冲、多目标交会轨迹的整体优化与带深空机动的多行星引力辅助轨迹优化类似，都是参数优化问题，且优化变量中都包含脉冲时刻、脉冲矢量等，因此可采用相似的方法进行求解.

3.2 多段小推力转移轨迹整体优化

对于多段小推力转移轨迹的整体优化问题，黄岸毅等[102]使用间接法进行求解，推导了中途交会和飞越的一阶必要条件，优化了与12个主带小行星交会的小推力轨迹.

唐高[103]提出了协态变量转换法，首先单独优化每段转移轨迹，然后引入缩放因子对各段转移的初始协态进行缩放，在不改变控制律的同时使质量协态在中途交会点连续，如图 3所示，从而使得内点约束中的横截条件自然满足.该方法可有效猜测每段转移的初始协态，提升了多段转移轨迹整体优化的求解效率.然而，该方法要求缩放因子为正数，当某段转移的初始质量协态大于1，会出现缩放因子为负数的情况，此时该方法不适用.此外，该方法不能为打靶变量中的中途交会时刻提供初值.Chen等[104]改进了协态变量转换法，取消了其缩放因子必须为正数的限制，扩展了适用范围，并在此基础上引入同伦法降低燃料最优问题的求解难度，但依然不能解决中途交会时刻的初值猜测问题.

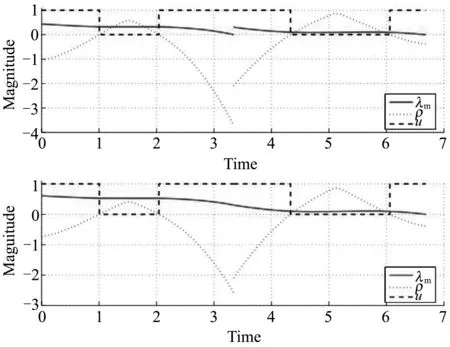
图3 质量协态λm、开关函数ρ、控制变量u在协态变量转换前后随时间的变化曲线(上：转换前，下：转换后[103])

3.3 小结

针对多段转移轨迹的整体优化，目前研究较少.其中脉冲转移轨迹的优化大多采用随机启发式算法求解参数优化问题，但无法保证解满足最优一阶必要条件.采用间接法优化小推力转移轨迹时，需推导一阶必要条件，从而将原问题构造为多点边值问题，然后通过打靶法求解，但如何有效猜测打靶变量的初值目前仍未完全解决，尤其是中途交会时刻的猜测还需进一步研究.

4 结论

本文从转移代价估计、交会序列优化、转移轨迹优化三个方面对多目标交会轨迹优化方法的研究现状进行了综述.转移代价估计中，数据库法和机器学习法的估计精度取决于数据库或训练神经网络所用数据集的大小，且针对不同问题需生成不同的数据库或数据集.解析法的估计精度取决于模型的简化程度，与原问题模型越接近，精度越高，但计算更耗时.针对不同的复杂动力学模型，仍需研究精度高、计算快的转移代价解析估计方法.交会序列优化中，集束搜索算法、分支定界法等树搜索算法和蚁群算法、遗传算法等随机启发式算法得到了广泛应用.目前的研究大多专注于解决单纯的组合优化问题，对于涉及交会时刻等连续变量的问题，还需研究更加高效的优化算法.转移轨迹优化中，多段轨迹整体优化的方法目前研究较少.针对多段脉冲轨迹的整体优化，需探究满足最优一阶必要条件的求解方法；针对多段小推力轨迹的整体优化，需进一步发展打靶变量的初值猜测方法，尤其是中途交会时刻的猜测方法.