立足经验生长 实现解答自然——以一道解析几何定值问题的教学为例

管良梁

(安徽省合肥市第四中学 233000)

解析几何为每年高考考查的热点内容，解析几何的大题基本上以准压轴题的形式出现，常与其他知识交汇命题，主要考查学生的逻辑推理能力和数学运算能力.由于解析几何大题涉及的知识面广、数学运算复杂等原因，导致学生在解答这类题时不知道从哪里下手.因此教师在讲解这类问题时一定要立足学生的经验，从学生最近发展区出发，使得问题的解答流畅、自然，易于学生理解.

1 例题呈现

(1)求椭圆C的方程；

(2)设椭圆C的右焦点为F，直线l与椭圆C相切于点A，与直线x=3相交于点B，求证：∠AFB的大小为定值.

①

②

又因为a2=b2+c2,

③

所以由①②③,得a2=3，b2=2，c2=1.

(2+3k2)x2+6kmx+3m2-6=0.

由Δ=24(3k2-m2+2)=0,得m2=3k2+2.

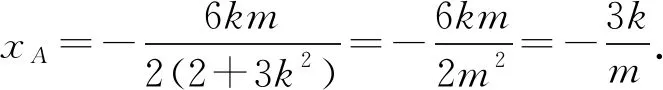
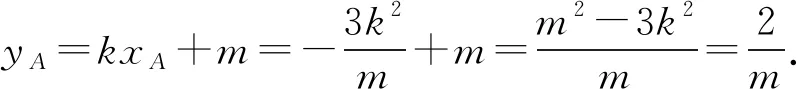
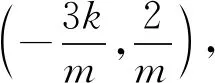
因为右焦点F的坐标为(1,0)，

所以∠AFB=90°.

即∠AFB的大小为定值.

2 途径尝试

2.1 从特殊情况出发

根据题意从特殊情况出发得出一个值(此值一般就是定值)，然后证明定值，即将问题转化为证明待证式与参数(某些变量)无关.

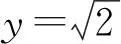
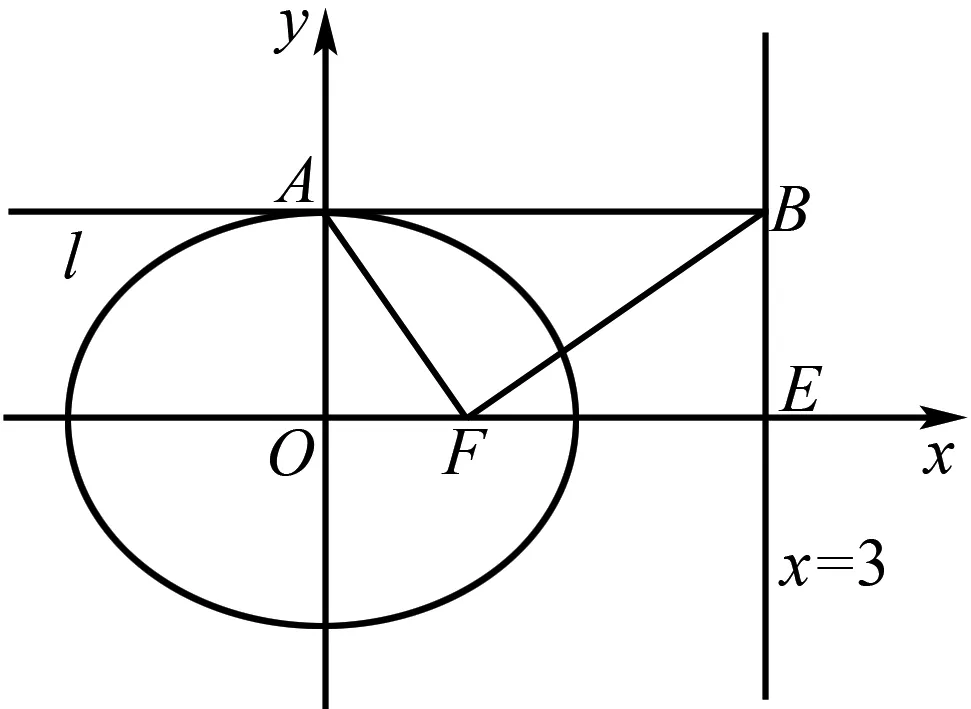
图1

由勾股定理，得

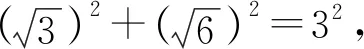
所以|AF|2+|BF|2=|AB|2.

由勾股定理逆定理可得∠AFB=90°.

②当直线l的斜率存在且不为0时，设直线l的方程为y=kx+m，直线x=3与x轴交于点E，如图2所示.以下同资料提供的解答.

图2

综上，∠AFB的大小为定值.

图3

2.2 从问题结论出发

将要证明的结论用动点坐标或动线中的参数表示，再利用其满足的约束条件使其绝对值相等的正负项抵消或分子、分母约分得定值.

|FB|2=4+9k2+6km+m2，

因为m2=3k2+2，

所以|FA|2+|FB|2-|AB|2

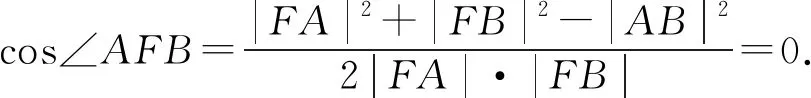
因为∠AFB∈(0°，180°)，所以∠AFB=90°.

点评解法2的思维非常简单，因为要证明∠AFB的大小为定值，所以只需要根据已知条件计算出cos∠AFB的值为定值即可.

3 结论拓展

4 总结反思

4.1 夯实基础知识

平时的教学要立足于课本，强化基础知识.教师应从教材的例题和习题中寻找试题的“根”，加强基础知识的复习，要列出具有典型性和代表性的题目进行讲解分析和训练，而且还要进行一题多变的训练.通过对题目的式子、图形、条件、结论、表达方式等的变化转换，促进学生触类旁通，巩固基础知识.

4.2 强化通性通法

在数学教学中，重视通性通法的使用和理解，通过通性通法揭示问题的本质.只有真正重视通性通法教学，才能使得学生抓住数学问题的本质，学生的核心素养才能得到提高.如解法1中，从直线l的斜率为0时开始研究，这样便于学生理解.

4.3 反思解题过程

在日常的教学中教师要指导学生如何进行反思，帮助学生养成反思的习惯.教师可以和学生一起回忆问题的解答过程，找出问题所在，帮助学生分析不能顺利答题的原因，提出改进方法.教师要带领学生立足已有的经验，从他们的最近发展区出发，思考有没有更简洁、更佳的解决问题的途径.学生在教师的带领反思中领悟方法，学会真正的反思，养成反思的好习惯.在反思中提升自我，提高解题效率.