对2022年高考乙卷理科数学第20题的多角度探析

金 毅

(内蒙古呼和浩特市第二中学 010000)

1 试题呈现

(1)求E的方程；

2 试题探析

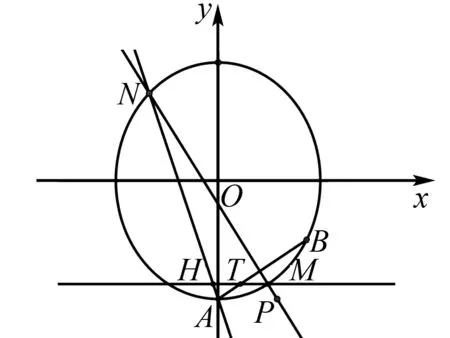
图1

探析1 (常规解法)设M(x1,y1),N(x2,y2)，当直线MN的斜率存在时，其方程可设为y=k(x-1)-2.

(3k2+4)x2-(6k2+12k)x+3k2+12k=0.

所以直线NH方程为

当x=0时，可得

由上可知，直线过点(0,-2).

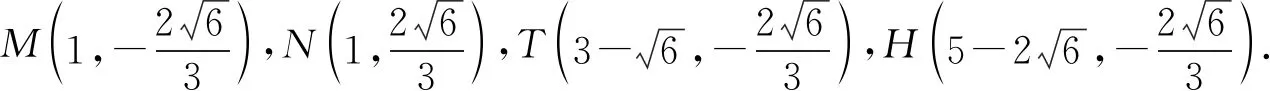
点评常规解法的关键是以点M的坐标为主，用点M的坐标表示点T,H的坐标，进而表示NH的直线方程.故常规解法的根本是要依托几何关系找到相关点的坐标，用坐标表示方程，进而完成解答.

因为点P(1,-2)在此直线上，可得恒等式

①

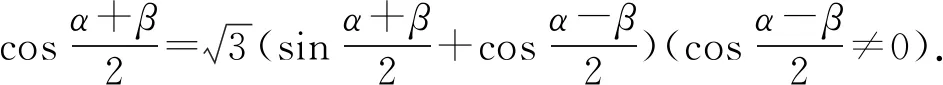
②

可得直线NH的方程为

根据①，事实上

所以直线方程可以写为

当x=0时，根据②，

所以直线过定点(0,-2).

点评本解法从椭圆的参数方程入手，首先用参数方程表示直线MN，因为点P在此直线上，所以可得到两个恒等式，之后写出直线NH方程，借助刚才得到的两个恒等式，化简了直线NH的斜率和纵截距的表达式，最后算出定值.

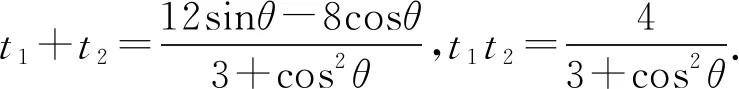
比较系数，可得

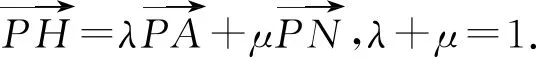
所以点H,A,N共线，直线NH过定点A(0，-2).

点评这个方法较好地发挥了直线参数方程的优势，用带有直线参数的坐标来表示向量.之后，通过对向量的运算以及比较系数，证明了向量线性表达式中系数和为1，进而证明三点共线.

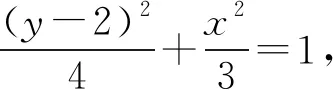
(4m2+3)y2+(8m-12)y+4=0.

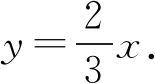
可得直线NH的方程为(y1-y2)x-(3y1-x1-x2)y-(x1y2+x2y1-3y1y2)=0.又x1y2+x2y1-3y1y2=(2m-3)y1y2+(y1+y2)=0.

所以可得NH通过点A(0，-2).

点评本解法的优点在于平移之后简化了直线方程，这直接简化了后续的计算量，比常规解法更加省时省力，解题时不妨一试.

探析5 (仿射变换)在用此方法解题之前，先给出几个引理.为方便证明题目，引理中所涉及点与题目中的点对应一致.

引理1 过圆(x-a)2+(y-b)2=r2(r>0)外一点P′(x0,y0)引圆的切线，切点为A′,B′，则直线A′B′的方程(切点弦方程)为(x0-a)(x-a)+(y0-b)(y-b)=r2.

引理2 给定一组调和点列N′,C,M′,P′，过这条直线外取一点A′，则称射线A′N′,A′C,A′M′,A′P′为一组调和线束.

引理3给定一个圆，以及圆外一点P′，过点P′作这个圆的切线P′A′,P′B′(A′,B′为切点)以及割线P′M′N′，那么A′N′,A′C,A′M′,A′P′是调和线束，从而N′,C,M′,P′是调和点列.

引理4 给定一组调和线束A′N′,A′C,A′M′,A′P′，过点M′作M′K∥A′P′,且M′K交A′C于点T′，则KT′=T′M′.(作任一调和线束的平行线，该线被其它线束平分)

其中，引理1来自于文献[1]，引理2,3,4均来自于文献[2]中定义4、性质4、性质7，限于篇幅，本文不再证明.

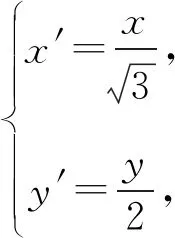
图2

又因为H′T′=T′M′，所以点H′与点K重合.故得到N′，H′，A′三点共线，则根据仿射变换的性质，直线在仿射后仍然为直线，所以N，H，A三点共线.

点评探析5揭示了本题的背景之一：调和点列与调和线束.如果在解决此题之前对这部分知识有相关的了解，那么解决本题时即可提前预知结论.

3 试题推广与探析

根据探析5，我们可以看到，本题与调和点列与调和线束有关，我们将从探析5出发，研究调和线束的一些解析几何性质.

探析6(初步推广，探析斜率关系)

证明命题1可用探析1至4的思路来研究，限于篇幅，我们使用探析4的思路.

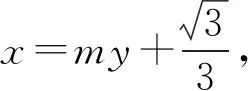
由韦达定理，可得

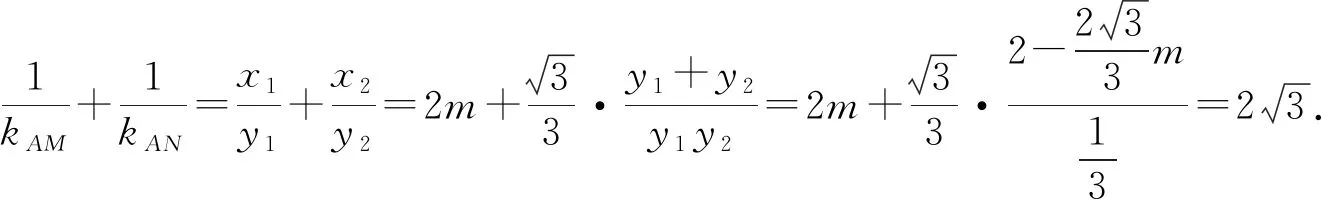
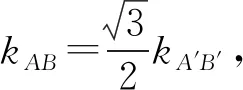
探析7(深入推广，探析一般情形)

图3

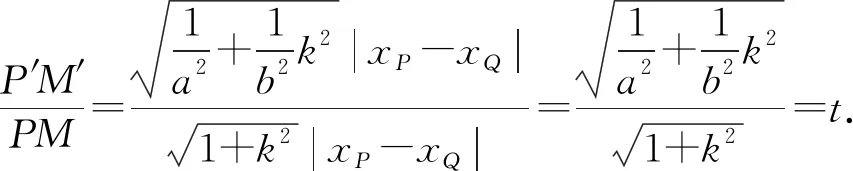
因为调和点列均在同一直线上，

当斜率不存在时易知结论成立，过程略.

点评命题3,4为命题5奠定了基础，命题5将调和点列这种线段的比例数量关系逐渐转化为斜率表达式，斜率本质是用来刻画几何中的位置关系的关键量.

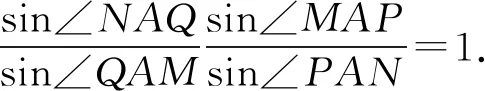
分别设调和线束AN,AQ,AM,AP的倾斜角为θ1,θ2,θ3,θ4，其斜率分别为k1,k2,k3,k4，根据三角形外角关系，

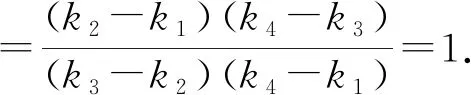
所以(k2-k1)(k4-k3)=(k3-k2)(k4-k1)成立.

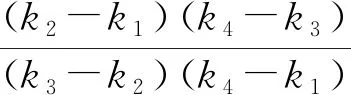
我们还可以得到以下类似结论，作为背景知识，以供大家参考.

4 进一步思考与总结

全国乙卷这道圆锥曲线问题以深刻的背景，清晰的表达，向我们呈现了一个图形鲜明，解法多样，层次多样的数学问题.本题深刻地、综合地考查了学生直观想象、数学运算、逻辑推理等数学核心素养，有较强的区分度.在平常的学习中，要特别注意对于背景结论的挖掘与反思，不能只停留在表面阶段.从几何到代数，再到算理，横向纵向多维比较才能真正做到通一类、会一类，研究透彻一类数学问题.今后的教学应以数学问题为导向，深入挖掘，多面剖析，才能达到真正理解数学问题，提高数学能力的目的.