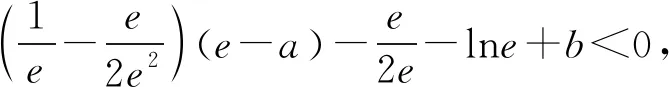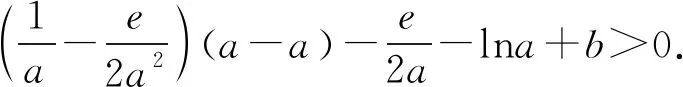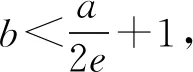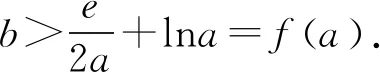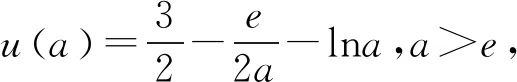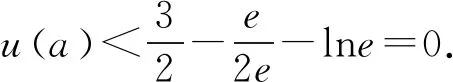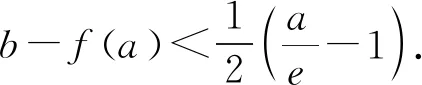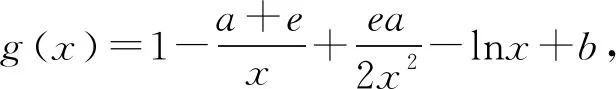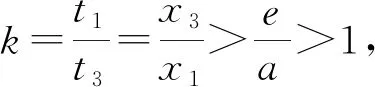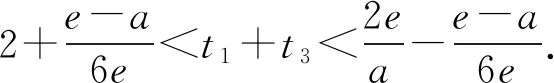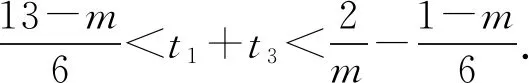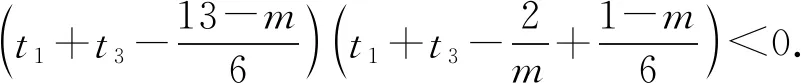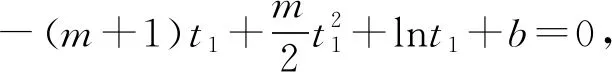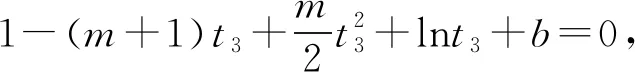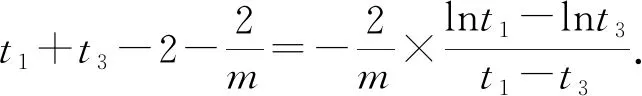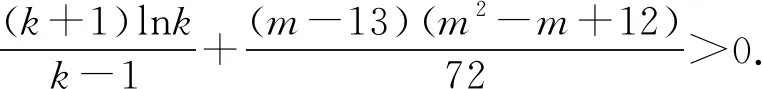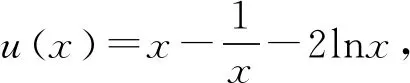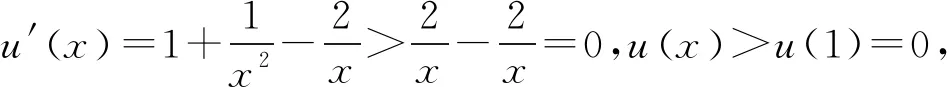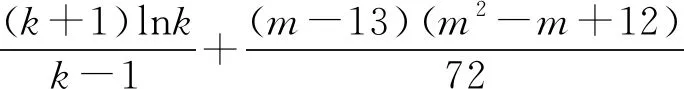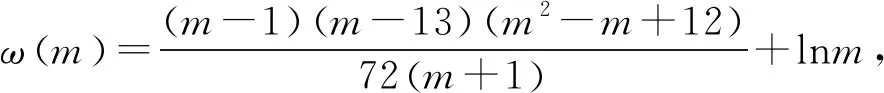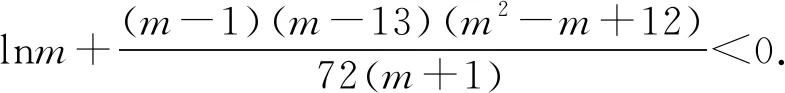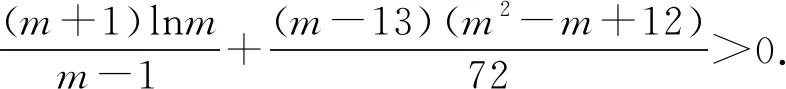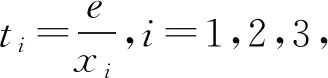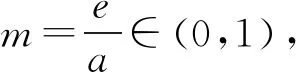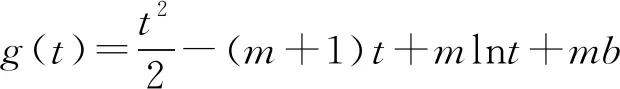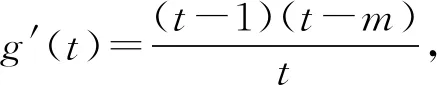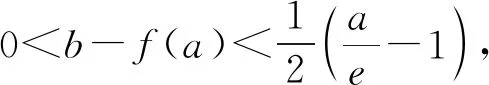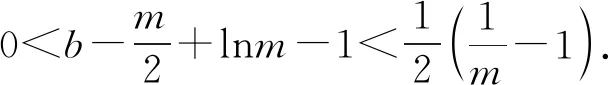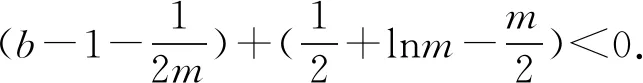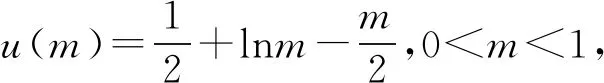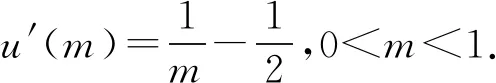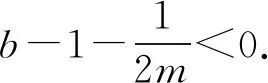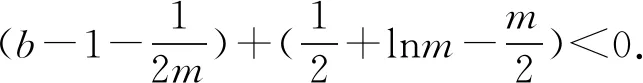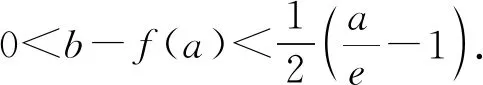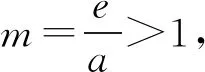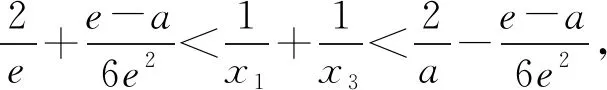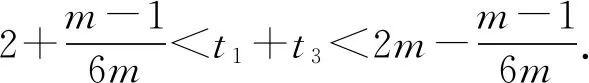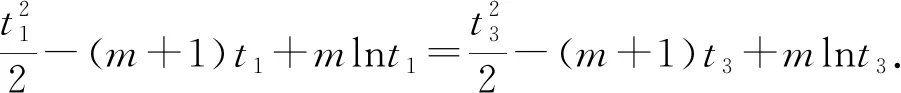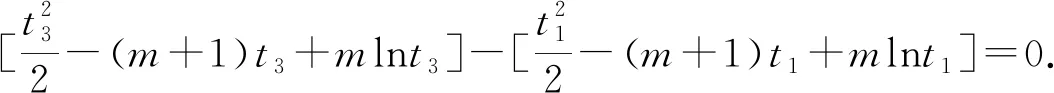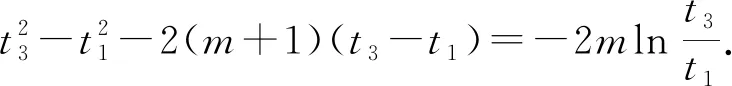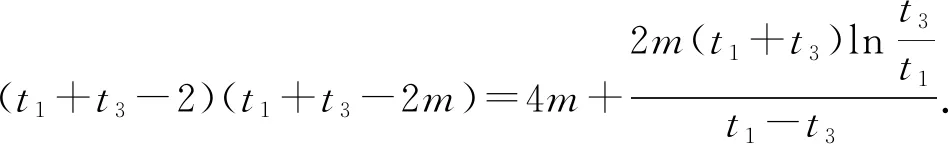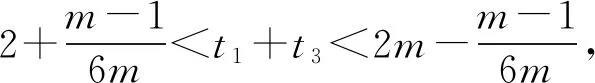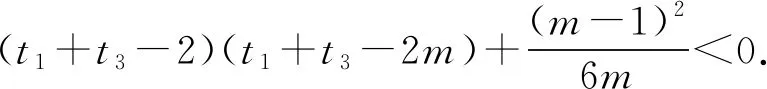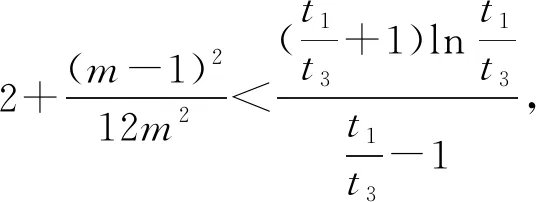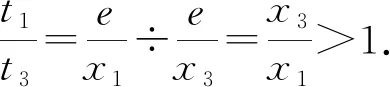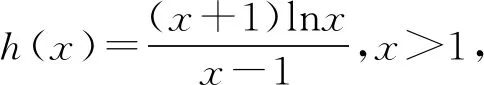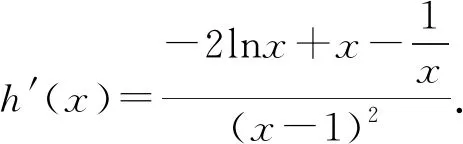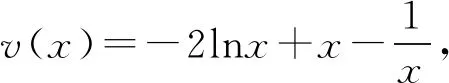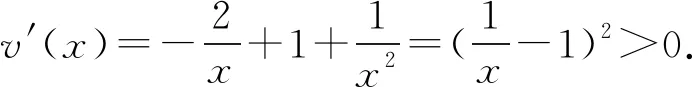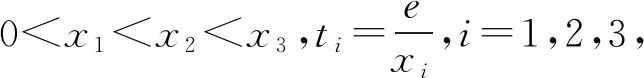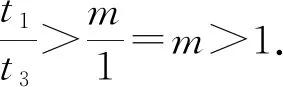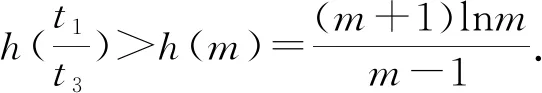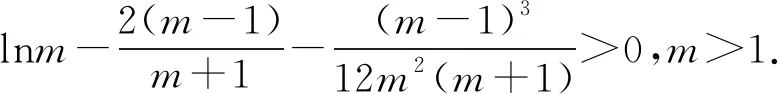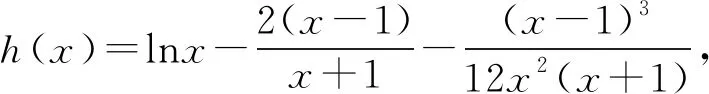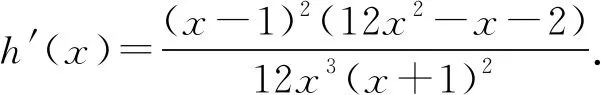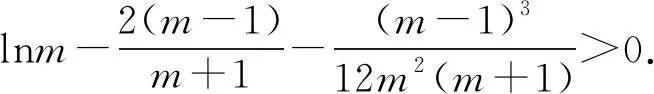2022年浙江卷第22题证法赏析

钟建新

(浙江省春晖中学 312300)

导数在高考中既是热点，又是难点，导数压轴是近几年浙江高考命题的一个特点，此类试题常涉及对考生逻辑推理、数学运算、数据分析等数学核心素养的考查.

1 试题呈现

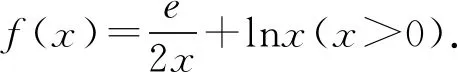
(1)求f(x)的单调区间；

(2)已知a,b∈R，曲线y=f(x)上不同的三点(x1,f(x1)),(x2,f(x2)),(x3,f(x3))处的切线都经过点(a,b)．证明：

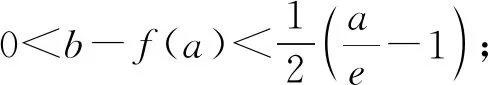
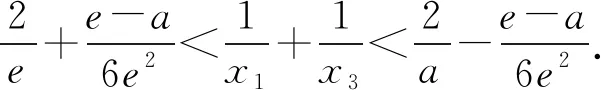
(注：e=2.71828…是自然对数的底数)

2 试题解析

2.1 第(1)问解析

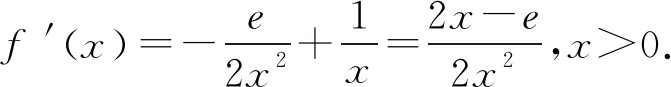
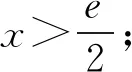
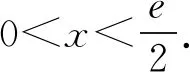
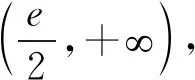
2.2 第(2)问解析

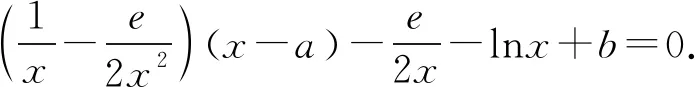
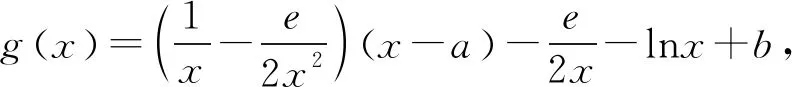
当g′(x)>0时，e

当g′(x)<0时，0a.

所以g(x)在(e,a)上单调递增，在(0,e)，(a,+∞)上单调递减.

因为g(x)有3个不同的零点，

所以需有g(e)<0且g(a)>0.

①

②

一方面结合②式可得b-f(a)>0；

所以u(a)在(e,+∞)上单调递减.

综合以上两方面，故有

(2)当0

因为g(x)有3个不同的零点x1,x2,x3，

故g(a)<0，g(e)>0.

又x1

这两式相减并整理，得

所以当x>1时，φ′(x)>0恒成立.

所以φ(x)在(1,+∞)上单调递增.

又k>1，所以φ(k)>φ(1)；

同理可证φ(x)在(0,1)上也单调递增.

又m∈(0,1)，所以φ(1)>φ(m).

所以φ(k)>φ(m).

所以ω(m)在(0,1)单调递增.

故ω(m)<ω(1)=0.

综上，原不等式得证.

证法2 (1)因为过(a,b)有三条不同的切线，设切点为(xi,f(xi)),i=1,2,3，所以过该切点的切线方程f(x)-b=f′(x)(x-a)有3个不同的根.

因为g(t)有三个零点，故需满足

所以u′(m)>0.所以u(m)

③

由③式即证

所以v(x)在(1,+∞)上单调递增.

所以当x>1时，v(x)>v(1)=0.

所以h′(x)>0恒成立.

所以h(x)在(1,+∞)上单调递增.

所以t1>t2>t3>0.

再结合g(t)在(0,1)，(m,+∞)上单调递增，在(1,m)上单调递减，且g(t)有三个零点可得0

所以当x>1时，h′(x)>0恒成立.

所以h(x)在(1,+∞)上单调递增.

所以h(m)>h(1)=0.

综上,原不等式得证.

点评(2)题的①构造切线方程，根据此方程有3个不同的根去证明不等式成立；(2)的题②用构造函数、分析法和导数去求证不等式成立，且上述两证法都用到了比值代换转化法.

代换法是解答高中数学习题的重要方法之一，在解题中有着广泛应用，通过对相关的数学表达式进行巧妙代换，能更好地揭示出相关参数之间的规律，再积极联系所学知识从而能实现顺利求解.