聚焦函数零点分布的常见题型及求解策略
2022-08-30李波
李 波
(四川省南充高级中学 637901)
1 回归定义,溯本求根

解析令f2(x)-mf(x)+m-1=0,
解得f(x)=1或m-1.
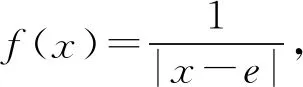

x1=e-1,x2=e+1.
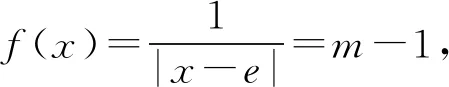
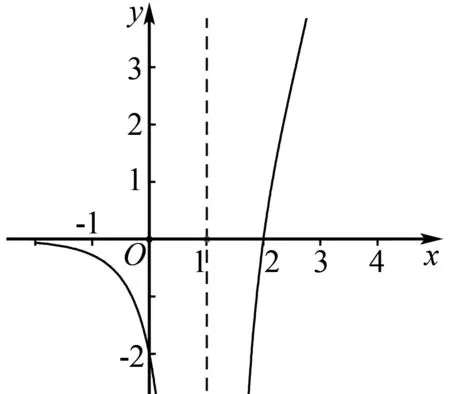
当x=e时,函数解析式f(x)=1,即x5=e.
综上所述x1+x2+x3+x4+x5=5e.

例2 (2019年全国Ⅱ卷文)已知函数f(x)=(x-1)lnx-x-1,证明:
(1)f(x)存在唯一的极值点;
(2)f(x)=0有且仅有两个实根,且两个实根互为倒数.


易知,当x∈(0,x0)时,f′(x)<0,当x∈(x0,+∞)时,f′(x)>0,即f(x)在(0,x0)上单调递减,f(x)在(x0,+∞)上单调递增.
所以当x=x0时,f(x)有极小值.
所以f(x)存在唯一的极值点.
(2)由(1)知,f(x)在x=x0处取得最小值f(x0)=(x0-1)lnx0-x0-1.

因f(e2)=e2-3>0,f(x)在(x0,+∞)上单调递增,所以存在唯一实数m∈(x0,+∞),使f(m)=(m-1)lnm-m-1=0.

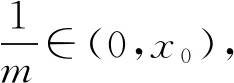
评析求函数零点的常用方法:一是通过解对应方程,求实数解;二是通过作函数图象,利用数形结合求交点横坐标,但需要注意函数的定义域,分段函数的零点检验.
2 巧用对称,不攻自破
例3 (成都树德中学期末考试)已知x1是函数f(x)=xlog2x-2020的一个零点,x2是函数g(x)=x·2x-2020的一个零点,则x1x2的值为____.
解析令f(x)=xlog2x-2020=0,得
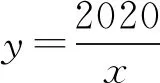
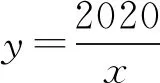
因函数y=log2x与y=2x的图象关于y=x对称,所以点A(x1,y1)与B(x2,y2)关于y=x对称,即y1=x2,y2=x1.
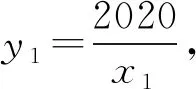
例4(2017年全国Ⅲ卷)已知函数f(x)=x2-2x+a(ex-1+e-x+1)有唯一零点,则a=( ).
解析f(x)=x2-2x+a(ex-1+e-x+1),令t=x-1,则g(t)=f(t+1)=t2+a(et+e-t)-1.
易知g(-t)=g(t),所以函数g(x)为偶函数.
又函数f(x)有唯一零点,所以函数g(x)也有唯一零点.
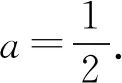
评析解决函数零点不可求的客观题时,要有二个意识:一是会转化,函数零点、方程的根、两个图象的交点三者之间等价转化;二是要有整体观,结合图象的表征深化到图象的对称性:中心对称、轴对称,奇函数或者偶函数的零点关于数轴原点对称,且所有零点之和等于0.
3 合理设参,统一变量
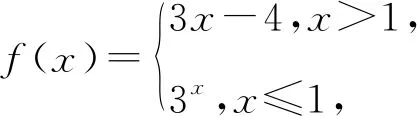
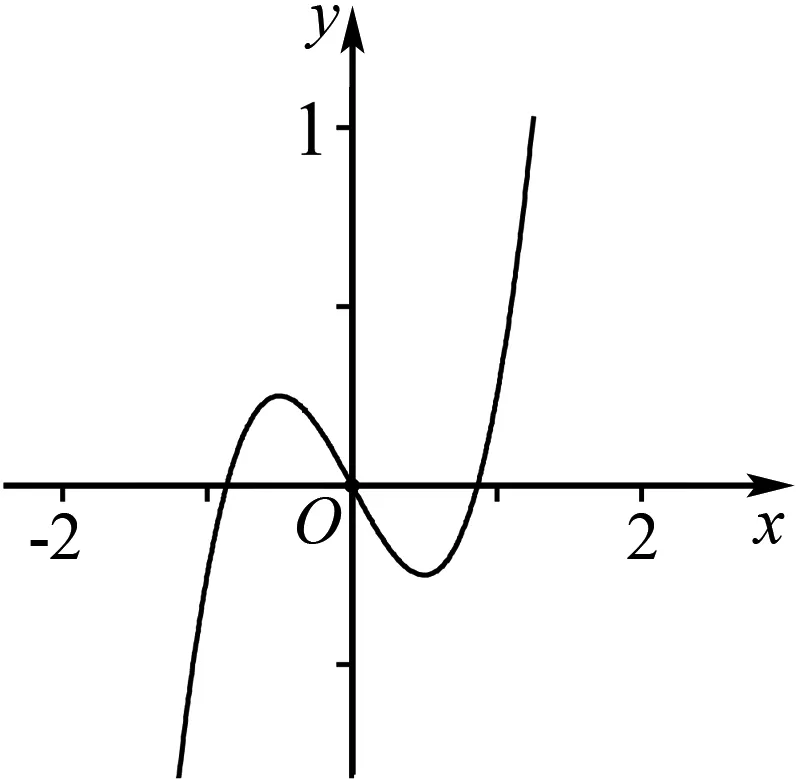
解析函数y=f(x)的图象如图1所示,令f(a)=f(b)=m,a 图1 又f(a)=3a=m,所以a=log3m. 由f(b)=3b-4=m,知3b=4+m. 所以a+3b=log3m+m+4. 构造函数g(x)=log3x+x+4,x∈(0,3],易知g(x)在(0,3]上单调递增. 所以g(x)的值域为(-∞,8]. 即a+3b的取值范围是(-∞,8]. 评析将方程问题转化为图象的交点问题,数形结合找到参数的切入点,联立方程组,将多变量问题转化为单变量问题,方便在化简、求最值时使用均值不等式、配方、构造函数判断单调性、比较大小等,但要注意变形过程的等价性. 解析函数y=f(x)的图象,如图2所示,令f(x1)=f(x2)=f(x3)=f(x4)=m,则m∈(0,1),0 图2 由f(x1)=f(x2),知|log3x1|=|log3x2|. 即-log3x1=log3x2,解得x1x2=1. 由f(x3)=f(x4)=m,知x2-10x+24-3m=0. 由根与系数的关系,得 x3+x4=10,x3x4=24-3m. ① (x3-3)(x4-3)=x3x4-3(x3+x4)+9, 将①式代入上式,得 (x3-3)(x4-3)=3-3m∈(0,3). 评析依据题目条件准确画出函数图象,使复杂的代数问题变得形象直观,结合图象建立等量关系、不等关系,求得零点的分布. (1)求b; (2)若f(x)有一个绝对值不大于1的零点,证明:f(x)所有零点的绝对值都不大于1. 图3 综上所述,当f(x)有一个绝对值不大于1的零点时,f(x)所有零点的绝对值都不大于1. 评析本题考查导数的几何意义、与零点有关的不等式证明,体现了数学运算、逻辑推理的核心素养.运用导数研究函数的零点或者方程的根,是高考热点问题,以函数的单调性为切入点,画出函数大致图象,以便确定函数零点的分布、最值情况,真正体现数形结合的灵活运用. 例8 (2020年浙江卷)已知1 (1)证明:函数y=f(x)在(0,+∞)上有唯一零点; 证明(1)由f(x)=ex-x-a知,导函数f′(x)=ex-1,显然,函数y=f(x)在(0,+∞)上单调递增. 又f(0)=1-a<0,f(2)=e2-2-a>0, 所以函数y=f(x)在(0,+∞)上有唯一零点. 故构造函数g(x)=ex-x-x2-1,x∈[0,1]. 所以g′(x)=ex-2x-1,g″(x)=ex-2. 令g″(x)=0,解得x=ln2. 易知函数g′(x)在(0,ln2)上单调递减,在(ln2,1)上单调递增. 又g′(0)=0,g′(1)=e-3<0,所以,当x∈[0,1]时,g′(x)<0,函数g(x)在[0,1]上单调递减. 所以h′(x)=ex-x-1,h″(x)=ex-1. 因为函数y=f(x)在(0,+∞)上单调递增, 评析本题给人以亲而不近之感,利用导数判断函数的单调性、零点个数,并将不等式的证明与零点的存在性定理完美结合,较好地考查了逻辑推理能力、转化与化归的思想. 例9(2016年全国Ⅰ卷)已知函数f(x)=(x-2)ex+a(x-1)2有两个零点. (1)求a的取值范围; (2)设x1,x2是f(x)的两个零点,证明:x1+x2<2. 由h′(x)>0知,x>1;由h′(x)<0知,x<1. 所以函数h(x)在(-∞,1)单调递减,在(1,+∞)单调递增. 当x∈(-∞,1)∪(1,2)时,h(x)<0; 当x∈(2,+∞)时,h(x)>0. 综上所述,h(x)的大致图象如图4所示. 图4 因为函数f(x)=(x-2)ex+a(x-1)2有两个零点,所以y=-a与y=h(x) 图象有两个交点,即-a<0,解得a>0. (2)由(1)知x1<1,x2>1,不妨假设x1+x2≥2,则x2≥2-x1>1. 由函数h(x)在(1,+∞)单调递增,知 h(x2)≥h(2-x1). 又h(x1)=h(x2),所以h(x1)≥h(2-x1). 整理,得(x1-2)ex1+x1e2-x1≥0,x1∈(-∞,1). 下证对任意的x∈(-∞,1),不等式(x-2)ex+xe2-x≥0恒成立. 令g(x)=(x-2)ex+xe2-x,x∈(-∞,1),则 由x<1知g′(x)>0, 即g(x)在(-∞,1)上单调递增. 所以g(x) 评析已知x1,x2是函数f(x)的零点,证明:x1+x2 函数零点的分布是难点,也是近几年高考的热点,综合性很强,考法灵活多变,解题时应该避重就轻,避实就虚,不失为一种明智的策略,可以考虑以上7种策略.考查了数形结合、分类讨论、函数与方程、转化与化归数学思想,也是解题策略的优化与变通,更是“临渊羡鱼,不如退而结网”的人生境界.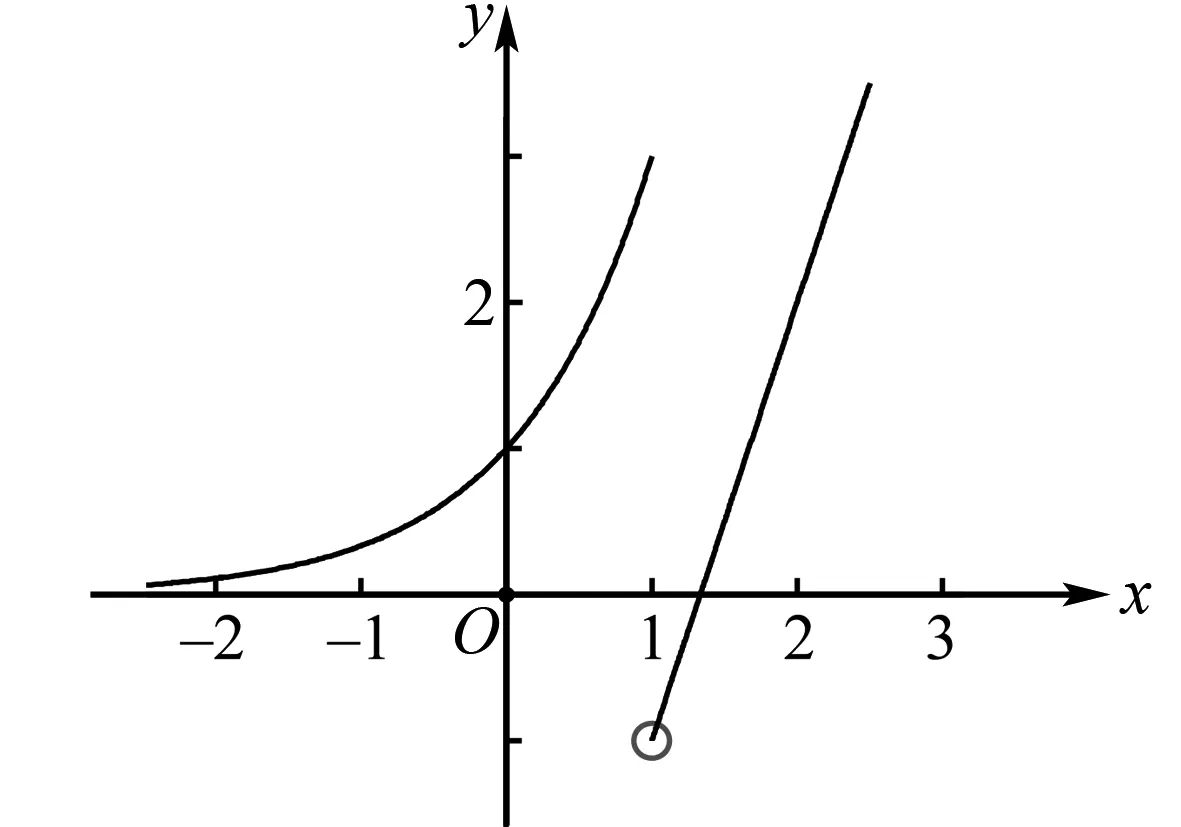
4 巧用模型,化动为静
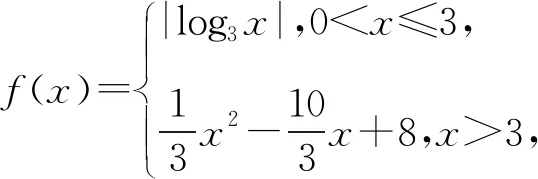


5 数形结合,相得益彰


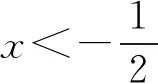


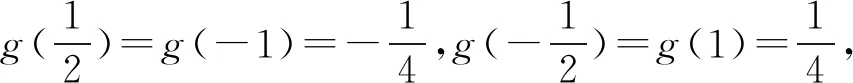
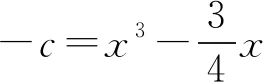
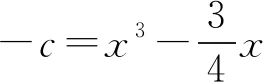
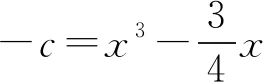
6 以退为进,海阔天空

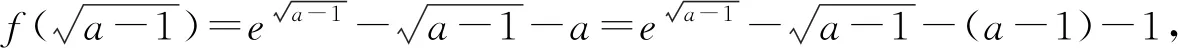

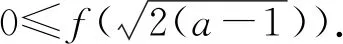
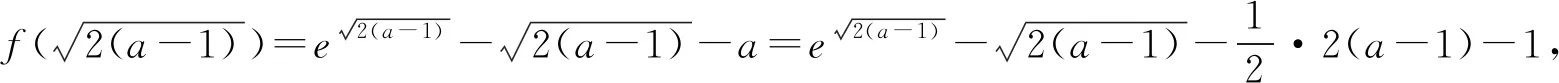
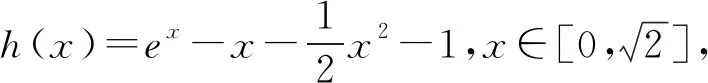
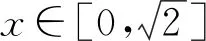

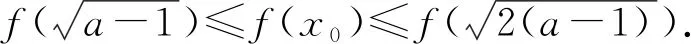

7 反面入手,柳暗花明