滑坡作用下X80腐蚀管道的极限宽度分析

2022-08-30唐雪梅刘思铭

中国地质灾害与防治学报 2022年4期

张鹏，唐雪梅，李虎，刘思铭

（1.西南石油大学土木工程与测绘学院, 四川成都 610500；2.四川省地质工程勘察院集团有限公司, 四川成都 610500；3.西南石油大学机电工程学院, 四川成都 610500）

0 引言

油气管道是国民经济发展的能源大动脉，在国家能源安全战略中居重要地位。截止2020年，我国油气管道总长度为14.4×104km，根据《中长期油气管网规划》，至2025年，国内油气管网规模将达到24×104km[1]。滑坡是引发管道失效的高频率地质灾害，是山区、野外管道防灾减灾的重点研究工作之一，如2017年7月2日，贵州省黔西南州晴隆县沙子镇段的中缅天然气管道在滑坡作用下发生断裂燃爆事故，造成8人死亡，35人受伤[2]，其中顺向层滑坡的稳定性最差、最易变形[3]。腐蚀是影响管道安全运行的危害因素之一，其尺寸和空间位置具有高度不确定性。当滑坡施加在管道上的拉应力、管-土交互作用以及内压荷载三者耦合作用发生在腐蚀处将严重影响油气管道的安全运营。

针对以上问题，学者做了大量研究，1998年，邓道明等[4]将滑坡作用下管道简化为梁，最先推导出拉压当量轴力下管道内力、变形的计算公式。2012年，郝建斌等[5]首次将管道后土体简化为刚性楔体，对横穿滑坡下管道的推力进行了计算，表明滑坡土体、管径、埋深是影响滑坡推力的主要因素。Zahid等[6]考虑管-土耦合作用，建立埋地天然气管道在纵向滑坡作用下的有限元模型，分析了管道的极限轴向应变。2015年，张铄等[7]建立深层圆弧形滑坡作用下埋地长输油气管道的力学体系，并建立数值模拟模型进行管道应力的参数敏感性分析。2016年，Kuppusamy等[8]用数值模拟法对含交互腐蚀管道的屈曲强度进行了研究。2018年，徐鹏飞[9]运用ABAQUS建立含腐蚀管道在滑坡作用下有限元模型，对管道的剩余强度进行讨论。2020年，李非飞等[10]研究了X80单腐蚀管道的失效机理，并建立有限元模型，对管道腐蚀参数进行了分析，拟合了失效压力预测公式。然而，鲜有研究将滑坡宽度用作外部评判指标，以进行滑坡威胁下油气管道安全预警预报分析。

为此，创新性地提出将极限宽度作为一个判定指标，用于确定腐蚀管道的安全状态。针对不同腐蚀尺寸和空间位置，建立了有限元模型用于参数分析，研究了滑坡推力、管-土相互作用、内压下腐蚀管道的力学响应，探究了腐蚀管道的极限宽度随参数变化的敏感性，提出了可用于工程实际的临界滑坡宽度以及腐蚀的边缘影响位置。以期为腐蚀管道在滑坡灾害下的安全预警提供依据。

1 滑坡推力计算和极限宽度定义

1.1 管道及土体本构模型

土体本构模型采用运用最为广泛的莫尔-库仑模型，能较好反映土体本构关系[11]，且需要的土体参数容易测量。管道本构模型采用双折线模型[12]，为给管道提供安全预警和抢修时间，运用第四强度理论（Von Mises）作为管道失效判断准则，如式（1），以管道应力达到许用应力时认为管道失效，如式（2），按《输气管道工程设计规范（GB50251-2015）》[13]可得管道仅在内压下需达到的最小壁厚即计算壁厚，如式（3）所示。

式中：σ1、σ2、σ3——管道三个方向主应力/MPa；

σs——管道屈服应力/MPa；

[σ]——许用应力/MPa；

K—设计系数，埋地直管段的轴向应力与环向应力组合的当量应力时取0.9[14]；

φ——焊缝设计系数；

δ0——计算壁厚/mm；

P——内压/MPa；

D——管道外径/m。

1.2 管道横穿滑坡推力

在以往研究中滑坡推力普遍采用均匀分布[14−16]，忽略了滑坡区域的边缘滑坡力小于中间滑坡力的客观事实。当管道穿越土体分布较均匀的土质顺层滑坡或滑坡后缘呈马蹄形时，可假设管道受滑坡推力呈二次抛物线形状，管道横穿滑坡时，在滑坡区中部管道所受推力最大，则滑坡推力公式为：

式中：x——滑坡段管道位置/m；

q(x)——滑坡推力/（N·m−2）；

qmax——最大滑坡推力/（N·m−2）；

L——滑坡区宽度/m。

根据横穿滑坡时管道的受力特点，可将管道看作受滑坡楔形体的推力作用[5]，如图1所示，则最大滑坡推力公式计算如式（5）：

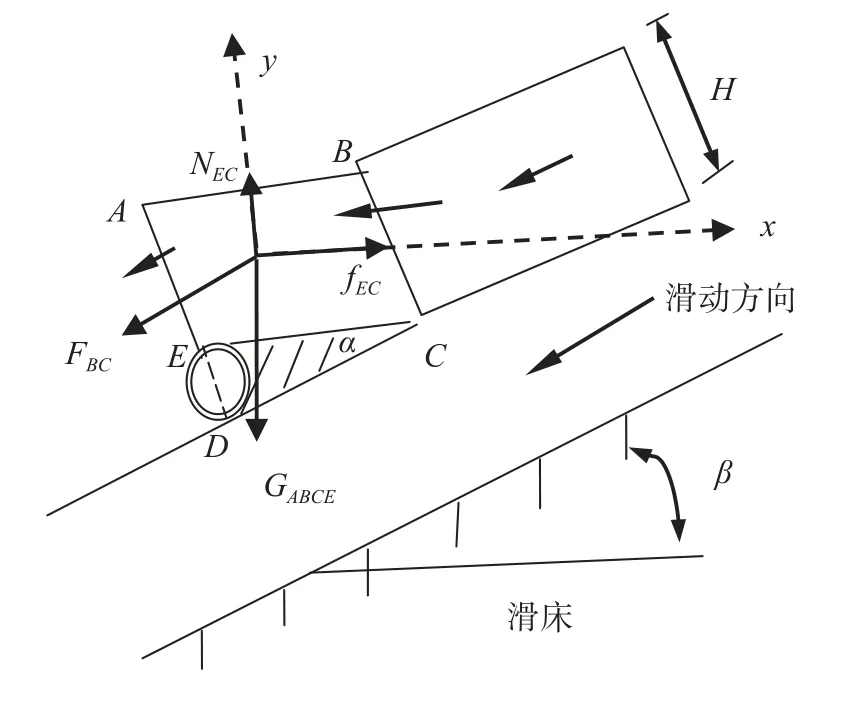
图1 滑坡楔形体受力分析图Fig.1 Force analysis of landslide wedge

式中：fEC——EC面滑坡推力/kN；

NEC——楔形体所受支持力/kN；

GCDE+p——滑块本身所受重力/kN；

α——滑坡水平角度/（°），工程上近似采用α=45°−φ/2；

D——管道直径/m；

φ——土体内摩擦角/（°）；

H——管道底面深度/m；

β——埋地管道与土平面夹角，近似等于该处滑坡倾角/（°）；

c——土体黏聚力/kPa；

t——管道壁厚/m；

γp——管道材料容重/（kN·m−3）；

γi——管输介质容重/（kN·m−3）。

1.3 管-土相互作用

滑坡发生时，滑坡体沿滑坡面向下滑动，推动管道产生应力和变形，但管道和土体的刚度差距较大导致两者变形量不一致，故管道与土体间是非线性接触且不协同变形，符合非线性接触模型。为真实反应管-土间的相互作用，在ABAQUS有限元中运用管-土非线性接触模型进行管-土间相互作用模拟。

1.4 管道的极限宽度定义

为给工程中横穿滑坡的管道安全状态提供一个外部预警指标，将管道应力达到许用应力时管道所能承受的滑坡作用宽度定义为滑坡作用下管道的极限承载宽度L（文中简称极限宽度）（图2）。

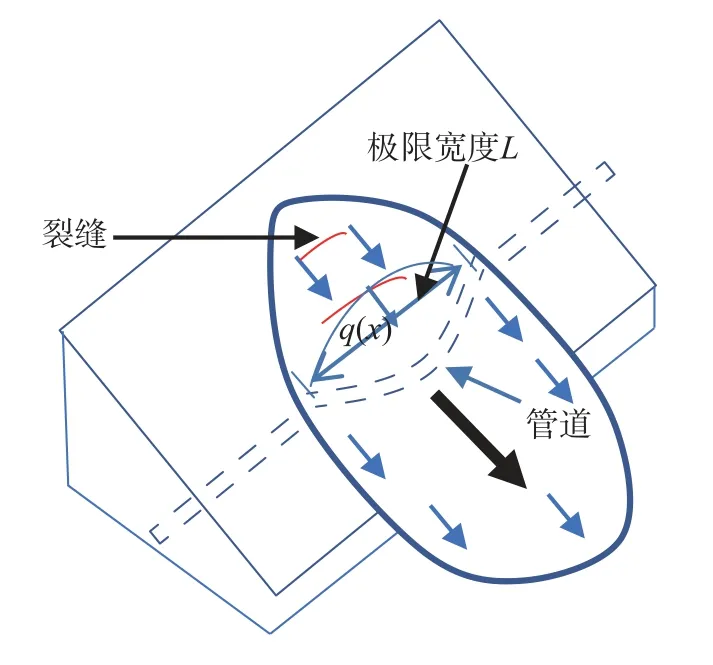
图2 管道极限宽度示意图Fig.2 Schematic diagram of pipe limit width

2 有限元模型建立

中贵线某滑坡平面形态呈马蹄形，滑坡后缘以斜坡陡坎为界，坡度约15°～30°，滑坡体宽度20～28 m，平均长度60 m，平均滑体厚3.0 m，是沿软弱带滑动的浅层土质滑坡，滑坡土体与非滑坡土体性质见表1[12]。X80管道横穿滑坡中部，管道埋深1 m，处于滑坡内部，管道内压为10 MPa，管道具体性质见表2[12]。

表1 土体参数Table 1 Soil parameters

表2 X80管材参数Table 2 X80 pipe parameters

2.1 模型建立

取滑坡坡度为30°，管材为X80管道，按式（2）计算出许用应力为499.5 MPa。建立滑坡作用下腐蚀管道的半模型，土体截面采用8 m×7 m，非滑坡区土体宽度不少于12倍管径[17−18]，取12.20 m，建立三个分析步，模型选取面面接触，管道外表面为主接触面，切线选用罚函数，摩擦系数为0.5，法向选用硬接触，运用式（5）计算出最大滑坡推力为93 709 N/m2，建立呈二次抛物线分布的力荷载q(x)，作用于管道滑坡区域迎滑坡面上，方向如图2所示。

2.2 模型网格敏感性分析

在划分模型网格时，为精确分析腐蚀处力学行为的变化且节约计算成本，需对管道厚度方向和腐蚀处进行网格细化[19]。以腐蚀长20 cm，宽3 cm，深0.2t即3.5 mm，滑坡作用宽度15 m，内压10 MPa为例（工况1），建立敏感性分析模型。

将腐蚀处网格尺寸按0.5 cm进行划分，其余部分按0.25 m进行划分，管道厚度方向网格依次划分为2～6层，且为验证非滑坡区土体宽度取12D时满足模型精度要求，以网格层数4层为例，建立非滑坡区长15D、18D的模型，提取各模型管道腐蚀中点处轴向路径应力，结果如图3所示。

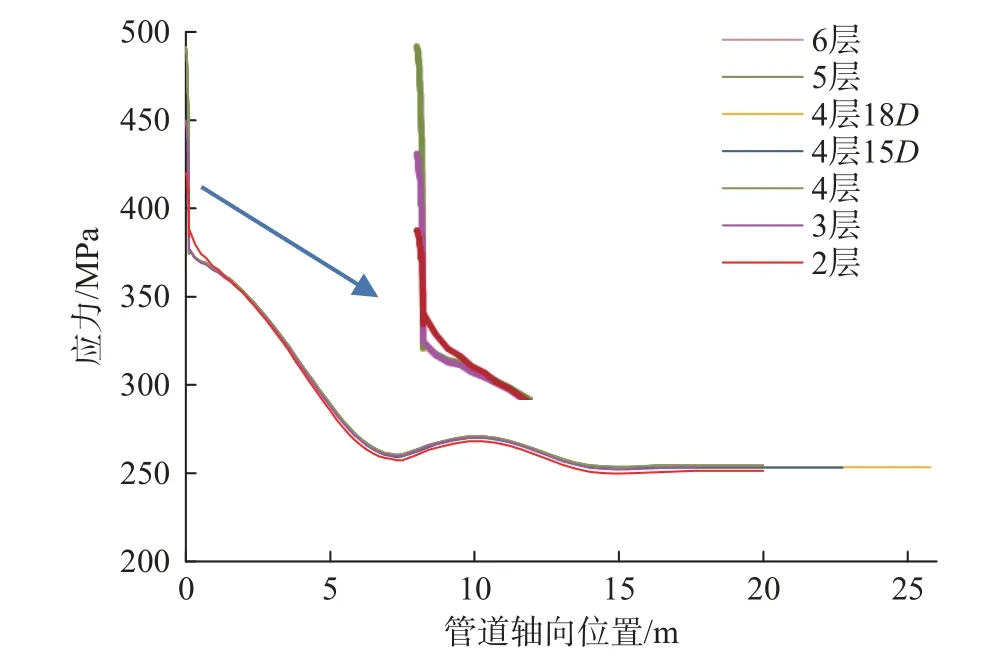
图3 管道厚度层数应力图Fig.3 Stress of pipeline thickness and layers

由图3可知，当管道厚度方向网格层数为2、3层时，网格精度不高，管道应力在腐蚀边缘处发生突变，管道最大应力偏小，曲线与4层时不重合；网格层数5层、6层时管道轴向应力与网格4层时完全重合，故为保证计算精度与节约计算成本可将管道模型厚度方向划分为4层；非滑坡区土体长12D时与土体长15D、18D时的管道最大应力相同，且轴向分布曲线重合，故非滑坡区土体宽度12D时满足模型计算精度要求。

为验证所选网格尺寸满足计算精度，建立网格层数4层，非滑坡区土体宽度12D，腐蚀处网格尺寸0.1 cm，其余部分网格尺寸0.1 m的网格细化模型，提取管道腐蚀中点处轴向路径应力，并与原模型进行对比，其结果如图4所示。

由图4可知，网格细化后的管道轴向路径应力分布与原模型轴向路径应力分布高度重合，管道最大应力偏差只有0.1 MPa，故可认为原模型的网格尺寸满足计算精度要求，后续模型网格尺寸按照腐蚀处0.5 cm，其余部分0.25 m进行划分，最终网格划分结果如图5所示。

图4 管道腐蚀网格宽度应力图Fig.4 Pipeline corrosion grid width stress diagram

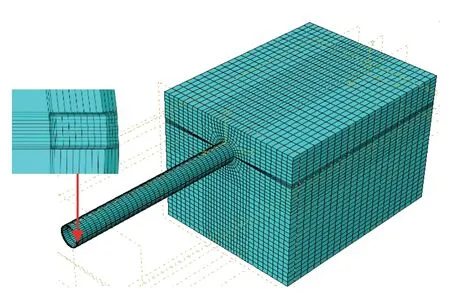
图5 模型网格划分Fig.5 Model meshing

3 腐蚀管道极限宽度分析

3.1 腐蚀尺寸影响

3.1.1 确定腐蚀尺寸

由于滑坡区中部管道所受推力最大，故将腐蚀建于管道滑坡区中部，以此研究腐蚀尺寸对管道极限宽度的影响。相关文献[11−12]研究表明，腐蚀宽度对管道承载能力影响较小，故暂不考虑腐蚀宽度对管道极限宽度的影响。按照《钢制管道管体腐蚀损伤评价方法（SY/T6151-2009）》[20]，管道腐蚀坑深度为壁厚的10%至80%时为2类腐蚀，可限期修复。按式（4）计算出管道的计算厚度为10.16mm，接近腐蚀深度达壁厚40%时的剩余壁厚10.5mm，管道腐蚀程度详细评价可见表3，结合研究[21]知，壁厚10%～30%的腐蚀最具有工程研究价值。

表3 管道腐蚀程度评价指标[22]Table 3 Evaluation index of pipeline corrosion degree

以坡面角度为30°，管道内压10 MPa为例，建立管道内腐蚀宽度为3 cm[12]，深度按壁厚的10%至30%间距5%确定，宽度取10 cm到30 cm间距5 cm的一系列模型进行腐蚀尺寸对管道的影响分析。

3.1.2 不同腐蚀尺寸的影响

为分析腐蚀尺寸和滑坡作用宽度对管道应力的影响，选取腐蚀深度0.2t即3.5 mm，建立不同滑坡作用宽度的管-土模型，对不同滑坡宽度下管道的应力进行分析，结果如图6所示。

图6 腐蚀深度0.2t时管道应力曲线Fig.6 Stress curve of pipeline with 0.2t corrosion depth

由图6可知，在达到屈服应力之前，随着滑坡宽度的增加，管道的应力不断增长；随腐蚀长度的增加，管道的应力也不断增加，且增幅减小，这是由于腐蚀长度增加时整个腐蚀面积增大，管道在腐蚀处的应力集中程度相对减弱；在接近屈服强度后，随滑坡宽度的增加，管道的应力缓慢增长；选用达到许用应力时的滑坡宽度为管道的极限宽度，为管道应力达到屈服应力时留有3m左右的安全裕度，可用于工程中在管道应力达到屈服前对滑坡进行处理或对管道腐蚀进行修复，并可对滑坡作用下的管道安全做出评判与预警。

为分析不同腐蚀尺寸对管道极限宽度的影响，以工况1为例，计算出腐蚀管道的极限宽度如图7所示。

由图7知，运用ABAQUS计算出无腐蚀管道的极限宽度为21.2 m，故无腐蚀管道的临界滑坡承载宽度为21.2 m；腐蚀深度为0.1t，长度为10 cm、30 cm时管道极限宽度分别为19.1 m、18.7 m，0.3t时分别为14.2 m、4.5 m，较0.1t时分别减小了0.35倍、3.16倍。可知随着腐蚀尺寸的增加，管道极限宽度不断减少，且管道的极限宽度对腐蚀深度表现出高敏感性。这是由于腐蚀深度的增加，导致管道壁厚的减薄，剩余壁厚逼近管道的计算壁厚，管道在内压与滑坡推力下容易直接爆管，故工程中应着重关注管道的腐蚀深度。

由图7还知，腐蚀深度为0.25t、宽度30 cm时，管道的极限宽度为10.4 m，腐蚀宽度越大，管道的极限宽度越小。工程中绝大部分滑坡的宽度均超过10 m，宽度小于10 m的滑坡在管道路线选取时可进行设置挡土墙或水泥护壁等处理，可忽略其影响，故建议在工程中应控制管道腐蚀深度不超过0.25t。

图7 管道极限宽度变化曲线Fig.7 Variation curve of pipeline limit width

3.2 腐蚀空间位置的影响

3.2.1 腐蚀径-环向位置影响分析

为研究腐蚀在不同径向位置、环向位置对管道力学行为及管道极限宽度的影响，以工况1为例，建立内、外腐蚀以迎滑坡面中点截面为0°，45°为间距逆时针变动的一系列模型，如图8所示，计算得到内、外腐蚀在不同环向位置管道力学行为，如图9所示。

图8 腐蚀环向位置示意图Fig.8 Schematic diagram of circumferential position

由图9知，随着腐蚀环向位置的变化，腐蚀位于迎滑坡面中点即0°时管道应力最大；内腐蚀管道应力始终大于外腐蚀管道应力，且曲线变化趋势一致，沿滑坡推力面中轴线呈对称分布；管道应力在0°～90°减小，90°～180°增大，这是由管道截面不同环向位置所受滑坡推力大小变化而致。即当腐蚀位于管道环向迎滑面中点处时，管道迎滑面受到滑坡推力作用使得管道发生挤压变形，应力变化最大，而背滑面则主要是由管道发生弯曲造成的管道背滑面处应力变化，未直接受到土体挤压作用，其应力变化相对于迎滑面较小，而管道上下两边则主要受到管道弯曲变形幅度最小，故而应力变化最小。且管道最大应力位置及管道最危险位置始终位于腐蚀处。

图9 管道内外腐蚀应力对比图Fig.9 Comparison of corrosion stress of internal and external pipeline

为分析腐蚀不同位置下管道与无腐蚀管道的环向详细的应力分布，提取无腐蚀和内腐蚀环向位置为0°～180°，滑坡宽度15 m时管道滑坡区中部内壁面的应力值，如图10所示，以及以腐蚀宽度20 cm，深度0.2t为例分析不同内、外腐蚀环向位置下管道的极限宽度变化规律（图11）。

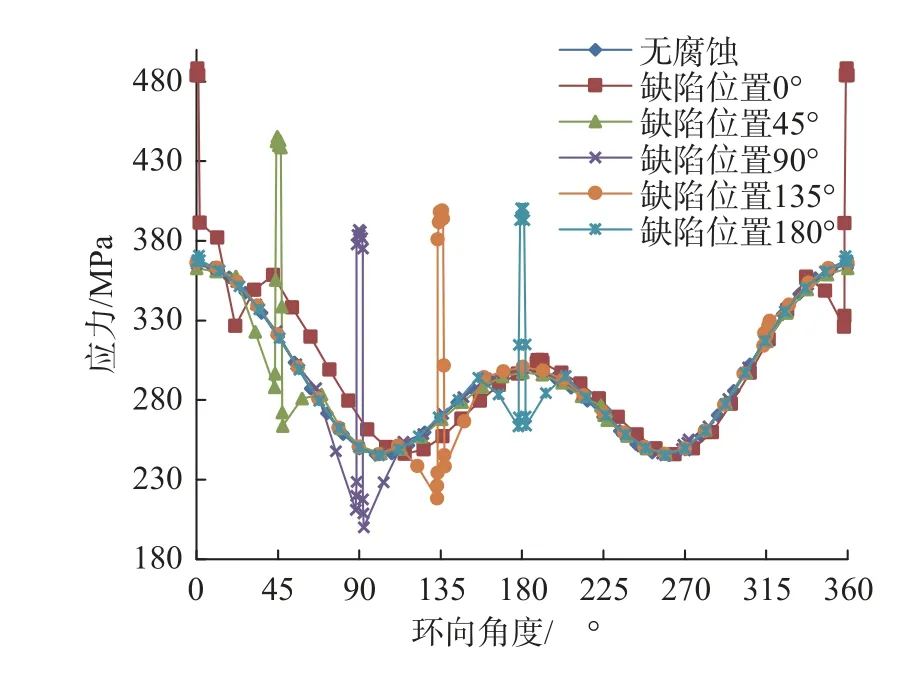
图10 管道环向应力路径图Fig.10 Pipeline circumferential stress path diagram

由图10可知，腐蚀管道沿环向上的等效应力在腐蚀处发生了突变，且应力远超相同滑坡宽度下无腐蚀管道的最大应力，故最大应力位置始终在腐蚀处，腐蚀两侧管道应力比无腐蚀管道应力小，其余位置处的应力及其变化趋势皆与无腐蚀管道相同，这由工况1的腐蚀深度较大导致。

由图11知，随着腐蚀在管道环向位置的变化，腐蚀位于迎滑坡面中点即0°时管道极限宽度最小，外腐蚀管道的极限宽度始终大于内腐蚀，即管道内腐蚀更加敏感。随着腐蚀位置沿管道环向变化，管道的极限宽度变化曲线成M型，沿滑坡推力面中轴线呈对称分布，即当腐蚀位于管道环向迎滑面中点处管道的极限宽度最小。随着腐蚀位置由管道环向迎滑面中点向两侧交界处移动，管道的极限宽度增大，由两侧交界处向背滑面中点移动，管道的极限宽度减小，最大与最小极限宽度值相差5.4 m。

图11 管道内外腐蚀极限宽度对比图Fig.11 Comparison diagram of limit width of internal and external corrosion pipeline

3.2.2 腐蚀轴向位置影响分析

为研究腐蚀在管道不同轴向位置下的力学行为及管道极限宽度的变化规律，以工况1为例，建立腐蚀由管道滑坡区中部向滑坡边缘移动，管道滑坡中部是0 m，间距为0.5 m的一系列模型，得到管道最大应力和极限宽度的变化规律，结果如图12所示。

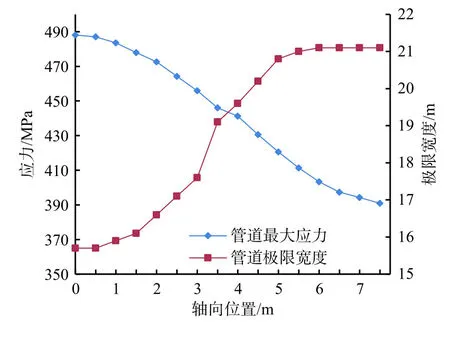
图12 不同轴向位置腐蚀管道的最大应力和极限宽度曲线Fig.12 Maximum stress and limit width curves of corroded pipes at different axial positions

由图12可知，腐蚀位置在管道滑坡区中部时，管道最大应力为488.1 MPa，比腐蚀在滑坡边缘时管道最大应力大97.2 MPa。可知随腐蚀轴向位置由滑坡中部向边缘移动，管道应力不断减小，减小速度先增大后减小，且最大应力位置始终处于腐蚀处，这是由所采用的腐蚀尺寸较大导致，对于较小腐蚀尺寸时，最大应力位置的变化情况可再进一步分析。

由图12还知，在腐蚀位置距管道滑坡区中部的距离不断增加的过程中，管道的极限宽度不断增加，且增速先增大后减小，增速在3.5 m处发生突变，当腐蚀位于管道滑坡区中部位置时，管道的极限宽度最小，为15.7 m；当腐蚀距管道滑坡区中部3.5 m时，管道的极限宽度为19.1 m，增量是腐蚀距管道滑坡区中部3 m时的3倍，且此后管道的极限宽度缓慢增加至稳定；当距管道滑坡区中部6m时，管道极限宽度为21.1 m，与无腐蚀管道极限宽度值相近。可知在腐蚀距管道滑坡区中部的距离小于3.5m时腐蚀对管道安全的危害较大，3.5 m至6 m腐蚀的危害不断减小，距管道滑坡区中部距离大于6 m的腐蚀对管道的极限宽度的影响可以忽略，工程中在管道铺设时应加强滑坡区中部左右6 m管道的防腐处理。

为充分分析无腐蚀和不同腐蚀轴向位置下管道的应力分布，提取管道轴向路径应力值，结果如图13所示。

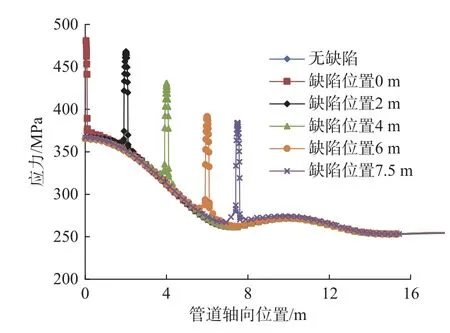
图13 管道轴向应力路径图Fig.13 Pipeline axial stress path

由图13可知，腐蚀管道轴向上应力在腐蚀处发生了突变，且始终大于相同滑坡宽度下无腐蚀管道的最大应力，分别为无腐蚀管道最大应力的133.8%、128.3%、118.23%、107.3%、105.4%，故管道最危险位置始终在腐蚀处，且由于滑坡作用使管道弯曲，距离滑坡中部越近，管道应力越大。结合图10、13可知，腐蚀仅影响管道在缺陷处的应力，对管道其余位置应力的影响可以忽略。

由以上不同腐蚀尺寸和空间位置下管道的极限宽度对比实际工况下管道受到的滑坡宽度，可初步判断管道的安全性。