水-力耦合及干湿循环效应对浅层残积土斜坡稳定性的影响

许旭堂，鲜振兴，杨 枫，刘道奇，简文彬，徐 祥，邵连金

（1.福建农林大学交通与土木工程学院, 福建 福州 350108；2.福州大学岩土工程与工程地质研究所, 福建 福州 350108）

0 引言

福建山区公路建设中存有大量的高陡边坡，路基的变形、稳定及病害处治等备受关注[1]。天然浅层土体长期受季节性气候变化的影响，土体原生结构发生改变，导致其抵抗外荷载的能力显著下降[2]。残积土滑坡作为福建省最主要的地质灾害，易受降雨的影响。雨水入渗过程中，因边坡内部水/气两相流发生运动，导致土体的微观结构、力学特性和有效应力状态发生改变，弱化土体的持水性能、渗流特性及边坡稳定性，引起坡体不可逆变形的发生以及滑面的形成与贯通。因此，开展水-力耦合及干湿交替对浅层非饱和残积土坡稳定性影响的研究，对此类路基边坡灾害防治与减灾研究具有重要的科学意义和现实意义。

非饱和土中的基质吸力对土的抗剪强度及路基边坡的稳定性有贡献。雨季浅层土坡失稳与湿润峰迁移引起的吸力损失有关，降雨条件下边坡暂态饱和区分布特征与演化规律以及地下水位变动所引起的坡体内基质吸力减小、抗剪强度降低和孔隙水压力提高是影响边坡稳定性的主要因素[3−8]。Song等[9]基于一维降雨入渗模拟试验，研究不同降雨强度作用下边坡内部岩土体基质吸力变化规律；曾铃等[10]研究了降雨入渗条件下坡体暂态饱和区的形成条件及多因素影响下暂态饱和区的分布；邱祥等[11]基于饱和-非饱和渗流理论，分析了不同降雨强度、饱和渗透系数、表面吸力、坡度条件下边坡降雨入渗影响区与暂态饱和区变化规律。

部分学者采用水-力耦合方法来考虑渗流过程中的土体变形。郑开欢等[8]建立温度场-渗流场-应力场耦合有限元模型，结合排土场边坡渗流场、应力场以及稳定性响应规律，提出基于边坡危险滑动带来讨论非均质边坡失稳特征。张良以等[12]基于膨胀应变与基质吸力增量的线性关系，在非饱和流-固耦合模型中引入膨胀性指标，建立一种适用于膨胀土工程的非饱和渗流场-应力场-膨胀应变场的多场耦合数值计算方法；熊勇林等[13]建立了一个基于有限元-有限差分理论的水-土-气三相渗流-变形耦合有限元数值分析程序，该程序可反映降雨入渗引起的边坡变形，边坡破坏先由坡趾面开始，逐渐向坡顶延伸最终形成连贯塑性剪切带。

以上研究都是基于非饱和土力学理论开展相关的渗流分析和水-力耦合分析，但对干湿循环效应下土体的变形和耦合行为对残积土边坡稳定性的影响仍需进一步解释。因此，本文利用Geo-studio软件的SIGMAR/W模块和SEEP/W模块模拟长时小雨下典型残积土边坡的水-力耦合及渗流效应，重点分析水-力耦合及干湿循环条件下坡体内部孔隙水压力、湿润锋及边坡安全系数的时空演变规律，以期为残积土边坡的长期稳定性评估提供参考。

1 浅层滑坡稳定性计算方法

降雨诱发浅层土坡失稳的滑面常平行于斜坡表面，考虑滑面具有较大的长深比，可进一步假定破坏的土块沿滑动方向无限延伸，按无限边坡进行分析。因此，可将斜坡的安全系数定义为土体的抗剪强度与滑面上的下滑应力的比值。

非饱和土抗剪强度中考虑用体积含水率函数来描述基质吸力对强度的贡献，形式如下[14]：

式中：τf——土体抗剪强度/kPa；

σn——法向应力/kPa；

ua、uw——孔隙气压力/kPa和孔隙水压力/kPa；

c'——有效黏聚力/kPa；

φ'——土体的有效内摩擦角/（°）；

θw、θr、θs——土体的体积含水量、残余体积含水率和饱和体积含水率。

根据式（1）及图1的计算简图[15]，无限边坡安全系数可表示为：

图1 无限边坡计算简图[15]Fig.1 Calculation diagram of infinite slope

式中：γ——土体重度/（kN·m−3）；

β——坡角/（°）；

z——坡体深度/m。

公式（2）表明边坡安全系数由与土体有效黏聚力、有效内摩擦角和基质吸力相关的变量组成。饱和状态下，uw≥0，且 ( θw−θr)/(θs−θr)=1，此时，土体非饱和状态下的抗剪强度向饱和状态时的抗剪强度转变，有效应力准则仍然适用。因此，对于处于水位以下的滑面仍然可以采用公式（2）对其进行边坡稳定性分析。

水-力耦合分析采用Geo-Studio中的Seep/W及Sigma/W模块完成。Seep/W基于加权余量的伽辽金有限元法，可对土体稳态或瞬态渗流进行分析，降雨条件下坡体内渗流场时刻改变，涉及饱和区和非饱和区的土体，需考虑瞬态渗流分析。Sigma/W可以使用一个完全耦合来求解土的固结问题，完全耦合分析需要对每个网格中的节点求解应力-变形和渗流连续性方程，以此给出位移和孔隙水压力的变化。Seep/W和Sigma/W数值分析所需的相关方程可参考相应手册[16−17]。

2 工程概况及计算参数

研究区位于福州福清福政大道至福人大道公路工程，该地段属剥蚀低丘，沿路线呈波状起伏展布，间夹宽缓的沟谷。该填方路堤段在原有基础上最大填筑高度约7 m，最终可形成一高12 m左右的高边坡，坡率为1∶1.5，钻孔资料显示该地段以残积黏性土为主，地下水位线位于2 m高程，该填方边坡典型剖面如图2所示。现场及室内模型试验表明[1,18]：土坡失稳破坏的范围集中在1.5～3.0 m。因此，选择0～3 m的浅层土坡作为分析对象，并将边坡简化为单一土层。

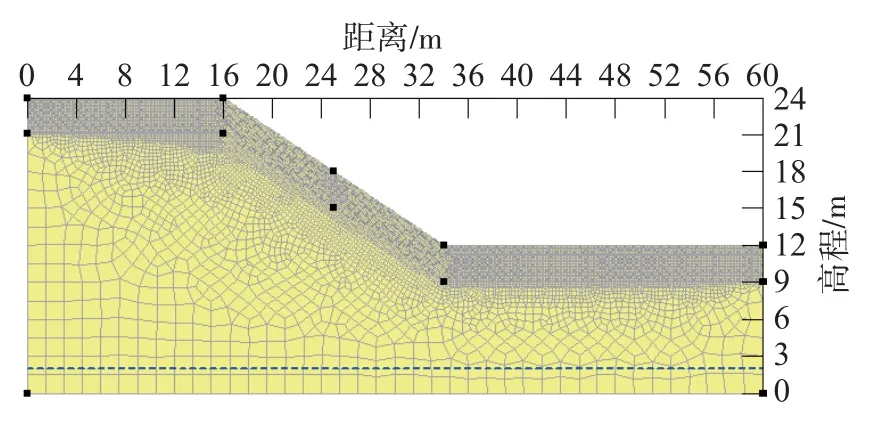
图2 路堤边坡典型剖面图Fig.2 Typical section of embankment slope

2.1 计算参数

X射线衍射表明残积黏性土体以石英、高岭石、钾长石等为主，残积土的颗粒级配曲线及孔径分布曲线见图3，土体液、塑限分别为43%、24%。干湿循环条件下残积土土-水特征曲 线（Soil WaterCharacteristic Curve，SWCC）可由应力相关的SWCC压力板仪系统测得（图4），天然浅层土体含水率变化大，现场勘查显示残积土质量含水率在17%至饱和含水率之间。残积土SWCC测定时，先对抽真空饱和后的原状土加压至1 000 kPa（此时对应的含水率约为17%），待试样排水稳定后，逐渐降低气压，此时土体缓慢吸水，重复上述步骤，直至完成目标干湿循环次数（1、2、3、5次循环）。整个干湿循环试验过程中，记录数据频次为每隔12 h一次，当24 h内试样吸水或排水的体积不超过土样体积的0.05%时，可认为吸力达到平衡[19]。渗流分析所需的渗透系数函数（HCF）由室内试验成果及参考类似工程[20−21]综合确定（图4），数值分析所需的参数见表1。土体SWCC曲线受孔径分布的影响，浅层土体长期处于湿热环境，土体裂隙发育，土体的孔径分布曲线（图3）表明其为双孔隙结构，土体内部所包含的大孔隙（裂隙）和小孔隙（土颗粒胶结孔隙）导致SWCC曲线呈典型的双峰特性（图4）。既有研究表明[22−26]：随着干湿交替的进行，土体饱和渗透系数（ksat）逐渐增加、有效黏聚力（c'）波动下降，而有效内摩擦角（φ'）则基本保持不变。由文献[19，22，23，25]及室内试验可得考虑水-力耦合及干湿循环的数值计算参数（表2），不同干湿循环次数数值计算所需的HCF函数与图4形式一致，这里仅考虑因干湿交替引起土体开裂而导致饱和渗透系数的变化。

图3 残积土颗粒级配曲线与孔径分布曲Fig.3 Particle gradation curve and pore size distribution curve of residual soil

图4 残积土土-水特征曲线及渗透性函数Fig.4 SWCCs and hydraulic conductivities of residual soil

表1 数值计算所需参数取值Table 1 Parameter value required for numerical calculation

表2 考虑水-力耦合及干湿循环的数值计算方案Table 2 Numerical calculation scheme considering hydrauliccoupling and dry-wet cycle

数值分析所需的非饱和条件下杨氏模量需通过构建孔隙比与双应力状态变量之间的关系曲面确定，但对于文中所研究的低渗透性的黏性土，建立上述曲面需耗费大量的时间。因此，文中基于SWCC曲线，采用文献[27]的半经验模型来预测杨氏模量随吸力的非线性变化，具体如下：

式中：Eunsat——非饱和条件下的杨氏模量/kPa；

Esat——饱和条件下的杨氏模量/kPa；

ua−uw——基质吸力/kPa；

Pa——用于维持方程左右两端单位一致的大气压力/101.3 kPa；

Sr——土体饱和度；

α、β——拟合参数。

根据文献[28]给出的不同土体特性及应力条件下拟合参数α、β的取值，低应力条件下拟合参数α介于0.05～0.15。因此，综合考虑土体塑性指数（文中为17）及文献[28]的经验取值建议，当拟合参数α和β定为0.1和1.2时，可较好的估算残积黏性土的杨氏模量（图5）。

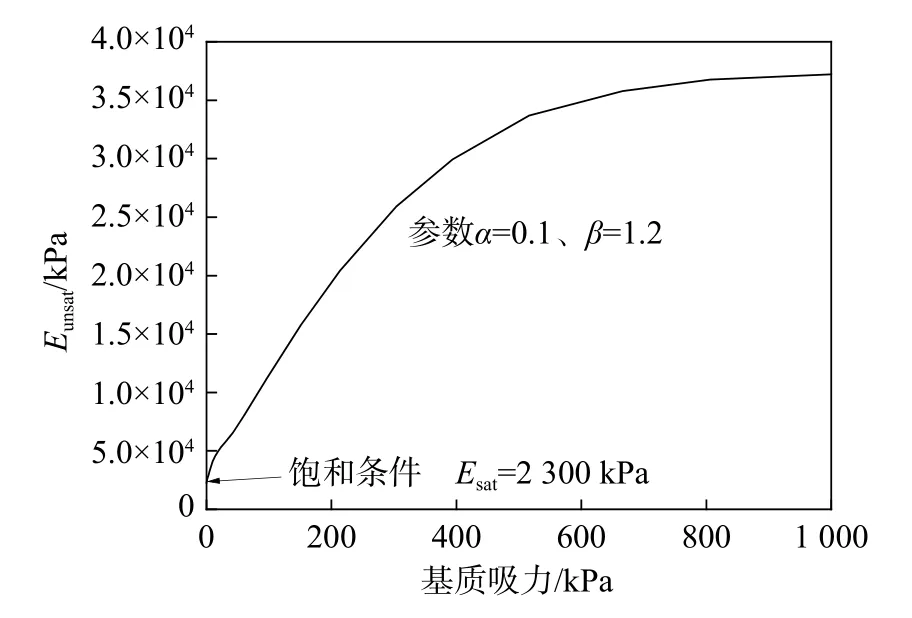
图5 半经验模型下土体Eunsat随吸力的变化曲线Fig.5 Variation curve of soil Eunsat with suction under semi-empirical model

由公式（3）可知：耦合分析中所用的杨氏模量具有时空效应，该模量随深度及降雨入渗时间的不同而不同。目前的SIGMA/W商业软件无法直接定义Eunsat随吸力的变化，Eunsat随吸力变化的精确解可通过数值积分技术（如：Euler积分求解）来获取，这里采用类似于有限元数值分析中非线性材料的切线刚度方法来实现Eunsat随基质吸力的变化。首先，将浅层土体分割成多个细土层（这里划分每个土层厚度为0.15 m，见图2）；其次，利用公式（3）计算上述各划分土层孔隙水压力时空分布曲线所对应的杨氏模量Eunsat的大小（图6）；最后，将图6的不同降雨时刻下Eunsat随基质吸力的变化结果更新于耦合分析中，以上耦合非线性方程的近似增量求解方法可较为准确的体现Eunsat与基质吸力的关系。为便于后续分析，本文选取的计算点有（图2）：上部、中部和下部土层，坐标范围依次为：（16，24）～（16，21）、（25，18）～（25，15）、（34，12）～（34，9）。

图6 中部土体Eunsat随时间和深度的变化曲线Fig.6 Variation curve of soil Eunsat with time and depth

2.2 计算工况及边界条件

依据气象部门对研究区的月降水量统计（图7），该地区年总降雨量为1 530 mm，降水主要集中于梅雨季和台风季，其中每年的5—8月（降雨量约占年总降雨量的55 %）为滑坡、崩塌、泥石流易发时段，尤其是经历长时梅雨季节后（前期有效降雨），后续更易出现台风暴雨诱发型滑坡[19，29]。因此，将年平均降雨量的55%（雨强大小约为2.4×10−3m/d）和3个月持时（梅雨季节为3—5月）作为耦合（考虑干湿循环效应）分析的流量边界（简化雨强略大于土体饱和渗透系数，按流量边界考虑，流量为简化雨强大小）。模型两侧饱和区（地下水位线以下范围）作为水头边界条件，模型两侧非饱和区为零流量边界，模型底部为不透水边界。长时小雨过程中，可能在坡表处形成暂态饱和区，即：地下水渗流可能沿着坡表溢出，因此坡表可定为渗流面。

图7 研究区月降雨量柱状图Fig.7 Histogram of monthly rainfall in study area

3 数值计算结果分析

3.1 干湿循环及耦合条件对孔隙水压力的影响

图8为考虑耦合及干湿循环次数下浅层土体孔隙水压力随时间和深度的变化趋势图。长时小雨条件下，边坡上部土体吸力显著下降，局部易出现暂态饱和区。降雨60 d后（图8），不同干湿循环次数下的边坡表面负孔隙水压力均增加至零，而坡体下部土层仍保留部分静水条件下的吸力。同一深度下（如：深度1.95 m处），干湿循环次数N=1，2，3，5对应的土体吸力分别为（图8）：81.5 kPa、56 kPa、26.5 kPa、10.2 kPa，这表明高干湿循环次数下湿润表层土体所需的时间更少。

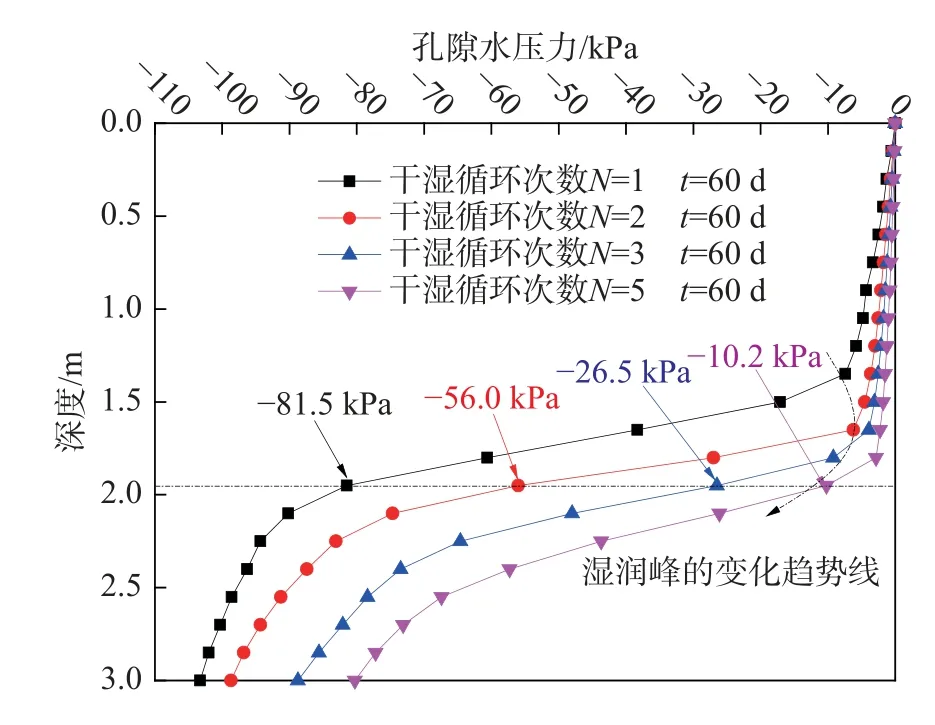
图8 干湿循环对浅层土体孔隙水压力空间分布的影响Fig.8 Influence of dry-wet cycles on the spatial distribution of pore water pressure in shallow soils

60 d降雨后，中部土体在1.95 m处的体积含水率变化更快，此时干湿循环次数N=1，2，3，5对应的土体体积含水率依次为：0.318 2，0.311 8，0.325 3，0.378 6（图9），由于干湿交替引起土体内部结构损伤，导致不同体积含水率对应的土体基质吸力不一样，如N=1，2时，虽然第二次的体积含水率小于第一次，但第一次干湿循环下土体的内部吸力却大于第二次干湿循环；随着干湿循环的推进，边坡土体逐渐软化，坡体内部体积进一步改变，从而引起土体吸力大幅度下降，导致湿润锋推进得更快（图9）。因此，在同一时间段内，随着干湿交替的进行，湿润锋的快速推进可引起越深位置的坡体孔隙水压力发生改变。

图9 干湿循环对浅层土体体积含水率空间分布的影响Fig.9 Influence of dry-wet cycles on the spatial distribution of shallow soil volumetric water content

3.2 耦合条件下干湿循环次数对湿润锋的影响

图10为不同降雨历时及不同干湿循环次数下土层湿润锋推进变化曲线。随着降雨的持续进行，雨水可逐渐入渗至土层深处，如干湿循环次数N=1，5时，整个降雨周期内湿润锋的位置依次为：0.45 m→0.75 m→1.2 m→1.35 m→1.65 m→1.95 m、0.75 m→1.2 m→1.65 m→1.95 m→2.4 m→2.55 m。干湿循环次数下越大，整个降雨周期内湿润锋可推进至更深位置，如：降雨历时为75 d时，干湿循环次数N=1，5时湿润锋的值依次为：1.65 m、2.4 m，增加幅度为45.5%。不同降雨持时后（15 d、30 d、60 d、75 d、90 d）干湿循环，湿润锋推进范围内的土体基本达到饱和状态，如整个降雨和干湿循环周期后，坡体的暂态饱和区域由0～0.45 m发展至0～2.55 m；而湿润锋前沿土体的吸力损失随着降雨和干湿循环的进行而快速丧失，土体含水率逐渐处于较高水平。

图10 干湿循环对湿润锋推进的影响Fig.10 Influence of the dry-wet cycle on the wet front propulsion

图11为不同降雨时刻下中部土层湿润锋处基质吸力随深度的变化曲线，Line1和Line2分别为降雨历时60 d和30 d时湿润锋的推进曲线，Line3为同一深度处（即：降雨历时60 d湿润锋所处的位置）土体的基质吸力值。同一时间下，干湿循环次数下土体润湿前深度所具有的基质吸力较低（Line1和Line2）；同一湿润锋深度下，随着降雨时间的推进以及干湿循环次数的增加，基质吸力下降的时空分布更为显著（Line2和Line3），如：湿润锋为1.75 m、1.95 m时，坡前吸力变化分别为：91.3 kPa→6.2 kPa、75.1 kPa→10.2 kPa。综上可知，雨水入渗速度与干湿循环次数有关，随着干湿循环次数的增加，湿润锋前沿更深，因湿润锋深度附近的基质吸力下降可导致安全系数进一步降低。

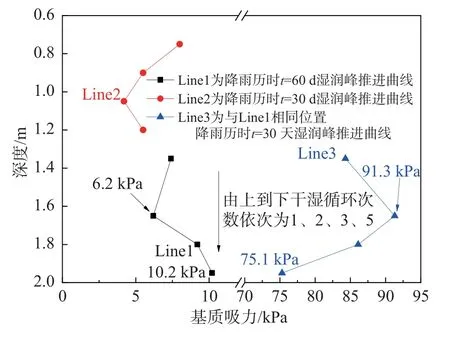
图11 不同降雨时刻土层湿润锋处吸力随深度的变化曲线Fig.11 Change curve of suction at the wet front of the soil layer with depth at different rainfall moments

3.3 耦合条件下干湿循环对边坡安全系数的影响

图12为不同降雨时刻下干湿循环次数对边坡安全系数的影响。整体上看，同一干湿循环次数下，湿润锋处的边坡安全系数随着降雨的进行而持续降低，但降幅有所减小，如：第1次干湿循环，整个降雨周期内边坡湿润锋处的安全系数分别为：4.92→3.11→2.24→1.96→1.66→1.53，降幅依次为：36.8%、27.9%、12.3%、15.5%、7.8%。同一降雨时刻下（降雨初期），湿润锋处的边坡安全系数随干湿循环次数的增加呈持续下降趋势，但在降雨后期，边坡安全系数降幅减小，如：降雨15 d、90 d，干湿循环次数N=1，2，3，5对应湿润锋处的安全系数分别为：4.92→4.26→2.94→2.16、1.53→1.28→1.12→1.02，下降幅度依次为：13.4%→30.9%→26.5%、16.3%→12.7%→9.0%，尤其是第5次干湿循环后，边坡安全系数为1.02（湿润锋推进的位置为2.55 m），处于临界失稳状态。

图12 干湿循环对边坡安全系数的影响Fig.12 Influence of dry-wet cycle on slope safety factor

降雨60 d时，不同深度的边坡安全系数随干湿循环次数的变化曲线可见图13。由图13可知：上部土层因应力水平低而具有相对较高的安全系数，随着降雨的持续进行，湿润锋逐渐向坡体内部推进，安全系数随之下降；受干湿交替的影响，雨水入渗引起湿润锋的推进速度和深度更快，直至可能出现局部最低的安全系数。值得注意的是：第1次干湿循环时，土体湿润锋处的安全系数为1.964，但整个浅层边坡的最低安全系数仍然处于最深处，由于土层上覆应力的影响，深部土体的剪应力更高，当雨水入渗不足以引起加剧土体强度的迅速下降时，此时边坡的安全系数由土体所具有的初期应力水平决定；但随着干湿交替的加剧，此时因雨水入渗引起深部土体基质吸力的大幅度下降，导致边坡的安全系数可在湿润锋的推进处达到最低值。

图13 边坡安全系数随深度的变化曲线Fig.13 Variation curve of slope safety factor with depth

4 讨论

Li等[30]指出降雨入渗下，只有当土体的有效内摩擦角小于边坡坡角时，湿润锋的迁移才可能导致浅层边坡的失稳破坏。当边坡坡角增加时，边坡浅层土体的稳定性会显著下降，即：陡坡可加大浅层滑坡的发生。由于湿润锋推进的过程中孔隙水压力为负值，因此，浅层边坡失稳破坏的条件为有效黏聚力和有效内摩擦角（式（2）的前面两项）对安全系数的贡献小于1。图14为式（2）前两项计算出的安全系数与深度关系曲线以及边坡破坏（Fs=1）所需的孔隙水压力大小，由图14可知：因湿润锋迁移导致边坡失稳所处的位置为2.4 m以下（区域3）。在区域3中，深度越大，边坡破坏所需的基质吸力也越大。在区域2内（深度范围1.65～2.4 m），正的孔隙水压力（地下水位上升）可导致边坡失稳破坏。在区域1内（深度范围0～1.65 m），由于边坡破坏所需的正孔隙水压力大于静水条件下的孔隙水压力，区域1范围内的边坡处于稳定状态。

图14 降雨诱发土坡失稳的破坏机制（第3次干湿循环）Fig.14 Failure mechanism of soil slope instability induced by rainfall(third dry-wet cycle)

图15为干湿循环次数对降雨诱发土坡失稳机制的影响。第1次干湿循环下，地下水位逐渐上升，此时非饱和区域逐渐向饱和区域过渡，土坡可因边坡内正孔隙水压力的增加而失稳（区域2，即：坡体位置为2.4～2.7 m）；随着干湿循环次数的增加，边坡失稳破坏不仅可因正孔隙水压力增加引起，还可因湿润锋快速推进、土体基质吸力损失而产生（即：区域3），并呈现区域3范围逐渐扩大的特点。第2、3、5次干湿循环下，区域3的范围依次为2.7～3.0 m、2.4～3.0 m、1.95～3.0 m，区域2的范围依次为：1.8～2.7 m、1.65～2.4 m、1.35～1.95 m，区域1的范围分别为：0～1.8 m、0～1.65 m、0～1.35 m，区域1和区域2的范围随干湿循环次数的增加而减小，表明边坡的长期稳定性应由湿润锋的迁移所引起的基质吸力和土体抗剪强度损失所控制，此时湿润锋前缘的安全系数为过渡区域内的局部最小值。因此，可以将其作为控制边坡长期稳定性的临界值。

图15 干湿循环次数下降雨诱发土坡失稳机制Fig.15 The mechanism of soil slope instability induced by rainfall under the effects of dry-wet cycles

综上所述，当湿润锋传播至区域3时，文中所分析的边坡才可能发生破坏；此外，破坏滑动面越深，所需的负孔隙水压力越小。因此，湿润锋迁移的速率对于浅层土坡的稳定性起着关键性的作用，湿润锋前沿越早入渗至区域3，土坡失稳所需的时间就越短。以上分析进一步解释了耦合效应及干湿循环次数对边坡长期稳定性的不利影响，单一考虑水力耦合效应而不考虑干湿交替的影响会过低的估计湿润锋的传播速度，导致具有更高的安全系数。同时，也应注意到土体所处实际湿热（或风干）环境，易引起其表层产生干缩裂缝，有利于雨水入渗，因此，采用压力板仪试验（即：封闭环境）获取的残积土干湿循环水力特性数据与实际有出入，由此计算得到的边坡浅层稳定性会较高。

5 结语

（1）第1次干湿循环下，坡体深处因具有高水平的剪应力而具有更低的安全系数。降雨过程中，湿润锋推进深度内边坡安全系数随着深度的增加而减小，与数值分析得到的孔隙水压力变化一致。

（2）随着干湿循环次数的增加，湿润锋的迁移速度进一步加快，孔隙水压力显著增加，水-力耦合分析下浅层残积土边坡更易失稳。干湿交替初期边坡可因正孔隙水压力(雨水入渗引起的地下水位上升)的增加而失稳，而干湿交替后期边坡可因湿润锋的快速推进(吸力损失)而破坏。

（3）干湿循环后期，耦合分析条件下的湿润锋迁移速率更快，土坡失稳所需的时间越短。边坡的长期稳定性受湿润锋迁移所引起的吸力和强度下降控制，可将湿润锋前缘的安全系数（局部最小值）作为评估边坡长期稳定性的临界值。

（4）文中虽然考虑了干湿循环次数的增加引起土体的开裂，进而导致饱和渗透系数变化，但未考虑体积变化对土体水力传导特性的影响。降雨入渗过程，土体孔隙比的变化可增加土体的透水性。因此，在耦合分析中，湿润峰前沿深度的增长速度可能更快。此外，可进一步开展降雨-蒸发循环条件（实际风干环境下）残积土边坡破坏机理试验研究，结合相似理论及数值模拟结果，对比分析湿润锋迁移速率及其引起基质吸力和强度下降规律，明确水力耦合及干湿循环条件下浅层残积土边坡的失稳机制。