标新而不立异 简约而不简单——从一道中考压轴题谈初高中衔接

广东省广州市第二中学(510040) 唐 琦

1 试题呈现

(广东中考第25 题)已知二次函数y=ax2+bx+c的图象过点(-1,0),且对任意实数x,都4x-12 ≤ax2+bx+c≤2x2-8x+6.

(1)求该二次函数的解析式;

(2)若(1)中二次函数图象与x轴的正半轴交点为A,与y轴交点为C;点M是(1)中二次函数图象上的动点. 问在x轴上是否存在点N,使得以A,C,M,N为顶点的四边形是平行四边形. 若存在,求出所有满足条件的点N的坐标;若不存在,请说明理由.

2 试题特色

第二小题是平行四边形的存在性问题,一般可用平移法或对角线法(中点法)解决问题. 在中考第二轮专题复习的教学中,教师也会设计一些特殊的几何图形的存在性复习专题,包括等腰三角形的存在性问题,直角三角形的存在性问题,平行四边形的存在性问题,或者特殊的平行四边形(如矩形,菱形,正方形)的存在性问题等. 本文主要针对第一小题分析.

2.1 问题新颖,条件简约

待定系数法求函数的解析式是初中函数教学的一个重要知识点, 也是考试中最常考的题型之一. 一般的问题设计都是函数图象经过特定具体的点, 将这些点的坐标代入到函数解析式中列出方程或方程组求出函数解析式中的待定系数. 本题先给出二次函数最常见的一般解析式y=ax2+bx+c,其图象过一个简单的点(-1,0),这一部分的条件比较常见,学生非常熟悉. 然后,马上又给出了一个连不等式,并且是一个任意性命题,超出考生的预料,让人觉得有些“猝不及防”. 有点像听一首歌曲前面平淡熟悉,突然曲风一转,引人入胜,耳目一新. 但条件依然简约,就一个解析式,一个点,一个练不等式,甚至不像第二小题那样题目条件变得更加复杂.

2.2 来源课本,初高衔接

从题目的形式看,让学生和老师“猝不及防”的原因可能有几个: 一是连不等式在平常的教学中不多见;二是二次不等式在初中数学的教学要求并不高;三是含参数的不等式在初中的思维性比较高;四是不等式的恒成立问题或者任意性问题在初中平常教学中不太常见,甚至有些老师也怀疑这是否超纲. 其实这些问题虽然不是常考的类型,但仍来源于课本. 以人教版为例,七年级下册课本第130 页习题4 中出现了连不等式的求解(如图1),第6 题的“盈不足”实际问题列出连不等式更加容易解决问题(如图2),九年级上册课本第47 页第5 题通过画二次函数图象的方式来求解二次不等式(如图3),九年级上册课本第17 页第13 题是有关含参二次方程的任意性问题(如图4).

图1

图2

图3

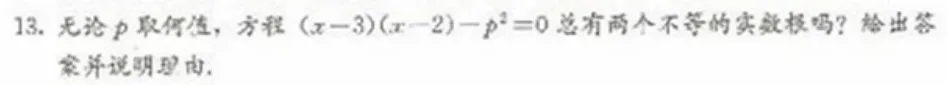
图4

通过和教材溯源比较,这些我们有些“猝不及防”的知识也都是在教材上的重点习题中出现,也更是初高中衔接的重点内容. 其中根据二次函数的图象来判断二次函数解析式中字母系数的特征,二次方程,二次不等式,二次函数这三个“二次”的结合问题都是初高中衔接知识的热点和重点问题.

3 解题分析

分析因为二次函数y=ax2+bx+c的图象过点(-1,0),所以首先肯定将(-1,0)代入解析式y=ax2+bx+c中,得到

接下来处理连不等式4x- 12 ≤ax2+bx+c≤2x2- 8x+ 6 这个条件了, 当然, 中间的二次函数的解析式ax2+bx+c参数较多, 不好直接处理, 反倒是第一个代数式4x-12 和第三个代数式2x2-8x+6 是确定的.首先我们就有一个思考, 对于任意的实数x, 根据不等式的传递性, 应该有4x-12 ≤2x2-8x+6, 但真的会这样吗? 不免就要产生要验证这个不等式的想法. 可以从“数”的角度验证, 我们使用作差法, 将2x2-8x+6 与4x-12相减,得到2x2-12x+18,即2(x-3)2,结果是非负数,所以4x-12 ≤2x2-8x+6 成立, 特别的, 当x= 3 时, 差为0, 即当x= 3 时, 4x-12 = 2x2-8x+6 = 0. 这时,0 ≤ax2+bx+c≤0,所以,当x=3 时,ax2+bx+c=0.

而另一个角度就是从“形”出发, 作出y= 4x-12和y= 2x2- 8x+ 6 的图象, 如图5, 根据图象我们可以发现,除了点(3,0),抛物线y= 2x2-8x+6 的其它各点都在直线y= 4x-12 上方. 也就是抛物线y= 2x2-8x+6 与直线y= 4x-12只有一个交点(3,0), 也就是抛物线y= 2x2-8x+6 与直线y= 4x-12 相切于(3,0). 根据连不等式4x-12 ≤ax2+bx+c≤2x2-8x+6 可知,二次函数y=ax2+bx+c的图象在抛物线y=2x2-8x+6 与直线y=4x-12 两者之间,且必然过点(3,0),直线y= 4x-12 同样也是抛物线y=ax2+bx+c的切线.

图5

而这个结果就令人喜出望外,根据前面的分析,必然有当x=3 时,ax2+bx+c=0,即

对这个不等式是一次不等式还是二次不等式进行讨论. 当a= 0 时,不等式就变成-4x+12 ≥0,不能对任意的实数x成立, 所以有a ̸= 0. 而当a ̸= 0 时, 不等式为二次式, 将ax2-(2a+4)x+(12-3a)看作一条抛物线的解析式,那么这条抛物线的点就要在x轴上或上方, 也就是抛物线与x轴只有一个交点或者没有交点, 画示意图可知:a ＞0 且Δ ≤0,即(2a+4)2-4a(12-3a)≤0,整理后得

两边约去16 得到a2-2a+1 ≤0, 即(a-1)2≤0. 而由平方的非负性(a-1)2≥0, 所以只能(a-1)2= 0, 非常巧妙甚至是巧合的得到a= 1, 所以二次函数的解析式为y=x2-2x-3.

从函数的图象来看,如图6,二次函数y=x2-2x-3的图象在抛物线y= 2x2-8x+6 与直线y=4x-12 两者之间, 且都过公共点(3,0),直线y= 4x- 12 同样是抛物线y=x2- 2x- 3 和y=2x2-8x+6 的切线.

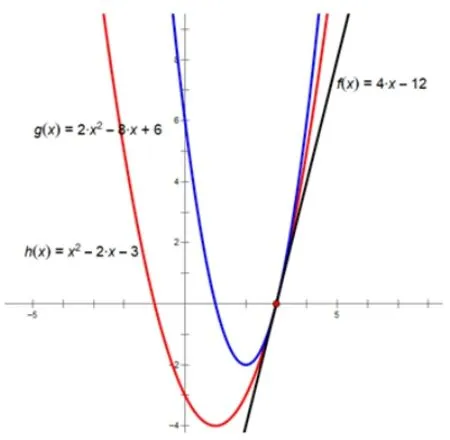
图6

当然, 从不等式③的分析看上去a= 1 的这个结果有些巧合, 自然我们也会考虑如果是从不等式④入手会不会更自然一点. 不妨试试看, 对任意的实数x都有ax2-2ax-3a≤2x2-8x+6,即

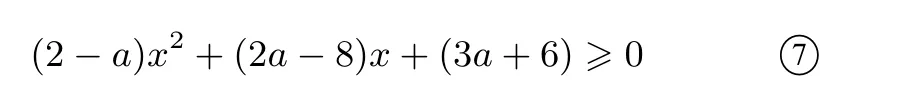
同样这个不等式是一次不等式还是二次不等式进行讨论. 当a= 2 时, 不等式变为-4x+ 12 ≥0, 同样不能对任意的实数x成立(这个结果和上述不等式③的结果竟然相同) . 而当a ̸= 2 时, 不等式⑦为二次式, 将(2-a)x2+ (2a- 8)x+ (3a+ 6) 同样看作一条抛物线的解析式,那么这条抛物线的点还是要在x轴上或上方,也就是抛物线与x轴没有交点或者只有一个交点,即2-a ＞0且Δ ≤0,也即a ＜2 且(2a-8)2-4(2-a)(3a+6) ≤0,整理得

(这个结果和上述不等式③的结果还是相同, 即不等式⑦⑧相同) , 后面的部分同理, 我们可以得到二次函数的解析式为y=x2-2x-3.

4 从高中数学的角度分析

以上在讨论不等式

两部分的过程中, 都非常巧合的出现了部分相同的运算结果, 如当分类讨论为一次不等式时, 两者都化为-4x+ 12 ≥0, 即4x- 12 ≤0, 而4x- 12 也恰好都是连不等式4x-12 ≤ax2+bx+c≤2x2-8x+6 的第一不等号前面的部分. 而当分类讨论为二次不等式,两个不等式的判别式⑦⑧也是相同,都为Δ=16a2-32a+16,从而根据非负性得到a= 1. 数学中一般不存在这种“巧合”的偶然性,应该有着必然性. 也就是这道题的数学本质是什么? 其实,如果从高中的观点来分析这道题的话,会更加容易挖掘这道题背后蕴含的内涵和本质.

我们再来看原题中最重要的这个连不等式条件: 对任意实数x, 都有4x-12 ≤ax2+bx+c≤2x2-8x+6.结合前面的分析, 我们不难发现: 如果不考虑二次函数y=ax2+bx+c的图象过点(-1,0)这个条件, 其实二次函数y=ax2+bx+c的图象是一条与直线y= 4x-12相切于(3,0) 的抛物线. 而且这条抛物线是夹在抛物线y=2x2-8x+6 与直线y=4x-12 两者之间.

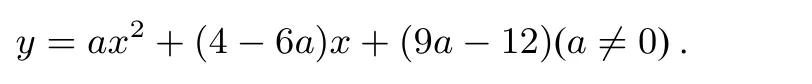
再来看抛物线还要满足是夹在抛物线y=2x2-8x+6与直线y= 4x-12 两者之间, 即满足对任意实数x, 都满足4x-12 ≤ax2+bx+c≤2x2-8x+6 的不等关系. 可根据图象与y轴的位置来处理,直线y= 4x-12 与y轴交于(0,-12),抛物线y=ax2+bx+c与y轴交于(0,c),抛物线y= 2x2-8x+6 与y轴交于(0,6),所以我们可以得到-12 ≤c≤6. 而c= 9a-12, 则-12 ≤9a-12 ≤6,解得0 ≤a≤2. 又a ̸= 0, 则0＜a≤2. 即对任意实数x, 都满足4x-12 ≤ax2+bx+c≤2x2-8x+6的二次函数y=ax2+bx+c(a ̸= 0) 的解析式为y=ax2+(4-6a)x+(9a-12)(0＜a≤2).

从高中数学的观点来看这道题, 我们可以归纳: 对任意实数x, 都成立

4x-12 ≤ax2+bx+c≤2x2- 8x+ 6 的二次函数y=ax2+bx+c的图象就是与直线y= 4x- 12 相切于(3,0) 的抛物线系. 而且这些抛物线是夹在抛物线y=2x2-8x+6 与直线y=4x-12 两者之间(如图7).

图7

这个抛物线系的解析式可以表示为y=ax2+(4-6a)x+(9a-12)(0＜a≤2). 当a= 0,y=ax2+bx+c的解析式就退化为一次函数y= 4x- 12. 当a= 2 时,y=ax2+bx+c的解析式就是y=2x2-8x+6.

5 教学导向

5.1 关注课本,“以本为本”

教科用书是集众多数学教育家和教育工作者智慧的结晶,其权威性和科学性毋庸置疑. 虽然作为教学的补充,市面上会出现各种让人眼花缭乱的教辅用书,还有随着信息技术的发展,各种超大容量的电子题库也层出不穷. 然而,越来越多有识之士达成的共识都是要把数学从题海中跳出来,我们的数学教学不只是简单机械的刷题,而是要更关注培养学生的学科核心素养,让学生养成终生学习,自主学习所必备的数学思想方法. 所以我们更应该追本溯源,回归课本. 课本中的每个知识的呈现, 每道例题和习题的设计都是大有深意,都是专家们在深思熟虑后最好的统筹. 我们在教学中可以在课本中挖掘更多的教学资源, 并且以课本为教学核心资源,不要被所谓的“学案”和“题库”牵着鼻子走,失去自己的教学节奏.

5.2 关注初高中衔接

中考作为初中生学业水平考试,也是学生进入高中学习的最重要选拔考试,逻辑的压轴题中更是成为一种新的趋势.从数学史的角度,数学学科知识的产生与发展和学生认知的过程不完全一致, 所以在教学中数学学科知识的呈现是以“螺旋式上升”的方式让学生更容易接受. 像小初衔接中的正负数,简易数轴,简易方程,简易不等式,几何图形初步,简单的统计等等. 而如果说初中的一般的教学内容难度为1 个单位,高中的相关数学内容难度为2 个单位,那么在中考的压轴题中对初高中衔接的考查设计到1.5 个难度单位,完全是可行而且是有必要的. 所以我们要加大初高中衔接的内容的重视度和关注度,在教学中,特别是压轴题的教学中,加大初高中知识融入和整合教学. 而从高中数学更高的角度来看初中数学,让我们对初中数学有更深入的理解和思考,教学教研上就可以有更充分的挖掘.

5.3 落实数学核心素养

教育的最终目的就是为了让受教育者能自主的学习. 数学教学不仅仅是教会学生数学知识,教会学生做题,更重要的是提升学生的思维逻辑水平, 培养学生的数学思想方法,落实数学学科素养. 而学科素养并不是一招一式中获取,也不是一课一时之中,而是在不断的积累中,在探究问题,分析问题,解决问题中最终落实. 这对我们老师对课程设计,教学活动组织,问题探究,资源整合提出了新的要求. 而从高观下,或者说另一个角度来理解教学,理解数学,就来更容易抓住教育教学的本质,更有针对性的培养学生的核心素养.