基于数学问题培养数学抽象素养的“U 型”教学模式*——以高三数学“数列重构”微专题复习课为例

广东省广州市荔湾区教育发展研究院(510375) 蔡 琳

《普通高中数学课程标准(2017 年版)》指出: 数学抽象是数学的基本思想,是形成理性思维的重要基础,主要表现为: 获得数学概念和规则, 提出数学命题和模型, 形成数学方法与思想,认识数学结构与体系.《标准》同时指出: 数学抽象素养的培养,要通过数学情境的创设、问题的驱动、过程的展开调动学生各种认知心理活动的参与[1]. 显然,“去情境”、“去过程”、“去反思”的表层教学模式,是无法促进数学抽象素养达成的,教师要积极构建深度教学模式,使学生的学习从浅层学习向深度学习转化,以使数学抽象素养落地.

“U 型”[2]是基于深度学习理论提出的, 深度学习理论认为, 学习是一个复杂的过程, 这个复杂的过程包括“下沉”、“潜行”与“上浮”三个阶段,这个过程像个“U 型”. 数学抽象与“U 型”十分契合,这种契合不仅表现在抽象的过程是一个“U 型”,更重要的是对学习结果的诉求都是素养. 故此,基于数学问题培养数学抽象素养,首先要经过“下沉”,进入知识内部结构,接着通过“潜行”经历抽象过程,认识结构,体悟学科思想方法,最后再通过上浮生成意义,如图1:

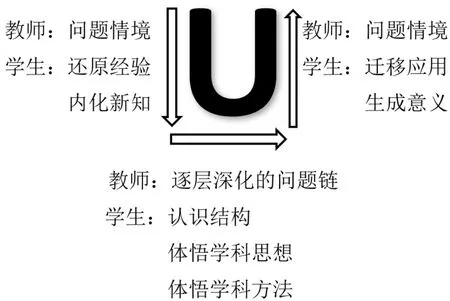
图1

本文以一节高三数学“数列重构”微专题复习课为例,谈谈如何落实基于数学问题培养数学抽象素养的“U 型”教学模式.

1 下沉：创设情境,直入知识内部结构

深度学习理论认为,知识的结构由内部结构和外部结构两部分组成,外部结构指知识的符号表征,内部结构包括学科思想方法和意义系统. 基于数学问题的“下沉”要以问题情境为载体,以问题为驱动,直入知识内部结构.

题组1 (1)若数列{an}满足a1=1,an-an-1=2n-1,求数列{an}的通项公式.

2 潜行: 认识结构,体悟学科思想方法

“潜行”发生在“U 型”底部,是一个“层进式”学习的过程. 基于数学问题培养数学抽象素养,教师需要遵循学生认知结构和知识内在结构,设计逐层深化的问题链,学生围绕问题经历观察与类化、抽象与概括、一般化与符号化等系列化的探究活动,在获得结构,体验与感悟学科思想方法的过程中发展数学抽象素养.

题组2 (1)若数列{an}满足a1=0,an+an-1=2n-1,求数列{an}的通项公式.

(2)若数列{an}满足a1=1,an+an-1=n2+1,求数列{an}的通项公式.

(3)若数列{an}满足a1= 1,an+an-1= 3·2n,求数列{an}的通项公式.

问题2 类比题组1 及其解题方法的获得,你觉得应该怎样找到题组2 解法的突破口呢?

师生活动: 学生在独立思考的基础上作答,师生共同明确: 题组2 解题的切入口需要根据研究数列的一般观念“运算”,计算特殊项找规律获得.

[设计意图] 以问题情境题组2 为载体,以问题2 为驱动,把学生的认知导向更深层——学科的“一般观念”. 章建跃博士指出: 学生如果能自觉地运用一般观念指导数学学习与探究活动,是学生学会学习的标志. 同时通过类比题组1 及其解题方法,引导学生观察与类化,这是数学抽象的基础.

问题3 完成表1,表2,表3,通过运算你发现了什么规律?

表1

表2

表3

师生活动: 学生独立完成表格的基础上,小组交流作答.

隔项作差,奇数项成公差为2 的等差数列(后项减前项),偶数项亦如此.

隔项作差,相邻奇数项的差成公差为4 的等差数列,然后累加(后项减前项),偶数项亦如此.

隔项作差,相邻奇数项的差成公比为4 的等比数列,然后累加(后项减前项),偶数项亦如此.

师生共同总结归纳表格内容和规律: 隔项作差,奇偶分组求通项.

追问1 你是通过怎样的运算发现规律的?

师生活动: 学生独立思考作答. 师生共同明确: 通过运算找规律,可以尝试相邻项或隔项作加、减、乘、除四则运算.

[设计意图] 问题3 借助表格直观, 引导学生运算与思考、探究与交流, 在观察与类化的基础上, 进行抽象与概括,并用自然语言予以表达,学生亲身经历探究活动,体验从特殊到一般, 从具体到抽象的数学思想和方法, 实现了“知其然”到“知其所以然”. 追问1 则实现了“何由以知其所以然”的跨越.

问题4 你能用数学符号语言表达隔项作差的结构吗?并完成题组2 的完整解答.

师生活动: 学生独立思考作答,师生共同明确: 把n赋为n-1,两式作差,可得隔项作差的新结构an-an-2=d(d为常数),或an-an-2=f(n),学生独立完成解答.

(2) 形如an+an-1=pn2+q,p,q为常数, 把n赋为n-1,两式作差,可得an-an-2=2pn-p,当n为奇数时,

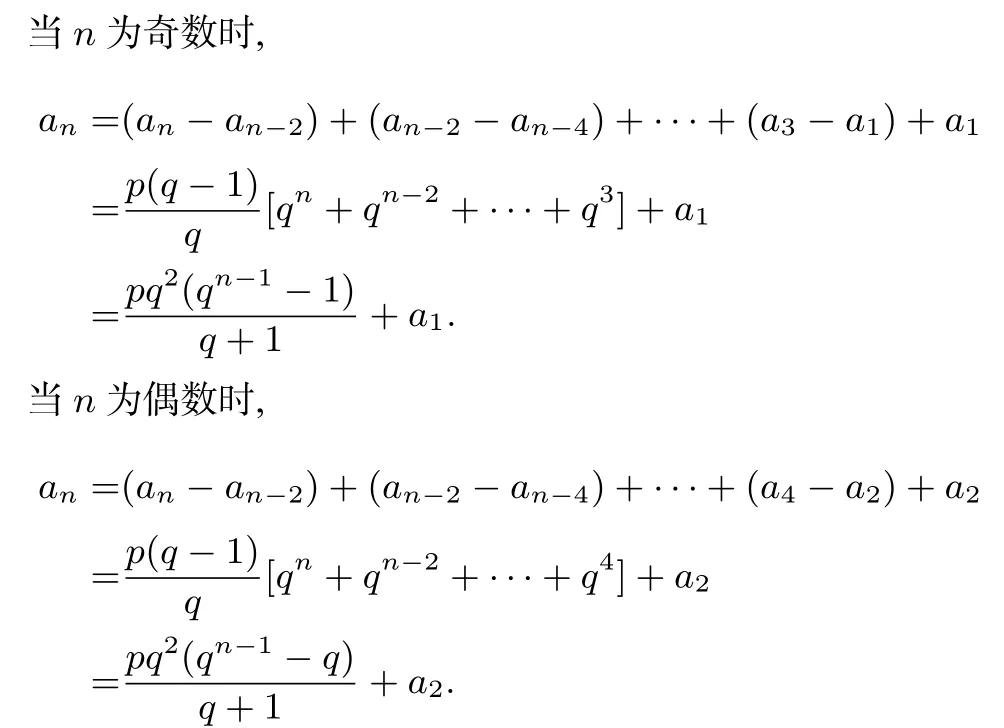
[设计意图] 追问1 把问题一般化、符号化,不但显现了一阶和式结构an+an-1=f(n)的本质,也是更高一级的抽象. 同时,数学问题一般化和符号化表达是数学具有高度抽象性的表现之一,在抽象与概括的基础上,学生需要展开一定的数学思维才能达到一般化和符号化的抽象高度,问题4为实现这一高度搭了一个脚手架.

问题5 回忆解决问题的过程,用到了哪些思想方法?

师生活动: 学生独立思考作答,师生共同总结归纳: 一阶和式结构an+an-1=f(n),需要把n赋为n-1,两式作差,重构新结构an-an-2=d(d为常数),或an-an-2=f(n),再奇偶分组求通项,在这个过程中,用到了从特殊到一般,从具体到抽象的数学思想和方法,积累了代数中把“运算”作为一般观念指导学习活动的经验.

[设计意图] 通过问题5,引导学生对知识进行联系性,结构化的梳理,深化学生对新知的理解和认知,有利于认知结构的改造和重组,形成稳定的认知图式. 同时深刻挖掘知识背后的数学思想方法,有利于核心素养的达成.

3 上浮: 迁移应用,生成意义

上浮是个体对学到的知识进行个人意义的升华和表达,是一个反思性思维和批判性思维形成的过程[3],经过这一过程,学生对知识进行反思,获得知识的内核,生成意义,从而感受知识背后的理性思维的力量,这也是数学学科育人的功能之一.

题3 若数列{an}满足a1= 1,anan-1= 2n,求数列{an}的通项公式.

题4 若数列an=2n,记bm为{an}在区间(0,m](m ∈N*)中的项的个数.

(1)求数列{bm}的前10 项和S10.

(2)你能提出更一般的问题吗? 并作答.

[设计意图] 题4(1)检测学生是否有意识能够在新的情境中选择和运用从特殊到一般的数学思想方法解决问题,属于思想方法的迁移,涉及较高级别的抽象. 题4(2)要求学生能够在综合情境中抽象出问题,并进行一般化、符号化,同时能用符号语言予以表达,涉及更高级别的抽象.

教师点评: 题4(1),从学生解答可以看出,学生能够通过运算,运用从特殊到一般的思想方法找到解题突破口,基本上能够做出解答:b1对应的区间为: (0,1],则b1= 0;b2,b3对应的区间分别为: (0,2],(0,3],则b2=b3= 1,即有2 个1;b4,b5,b6,b7对应的区间分别为: (0,4],(0,5],(0,6],(0,7],b4=b5=b6=b7= 2,即有22个2;b8,b9,b10对应的区间分别为: (0,8],(0,9],(0,10],则b8=b9=b10=3,即有3 个3;所以S10=1×2+2×22+3×3=19.

题4(2)是一个开放的问题,学生答案不唯一,下面是一位同学提出来的问题,并给出的解答.

问题求数列{bm}的前2t+1-1 项和S2t+1-1(t ∈Z+).

解答由S2t+1-1=1×2+2×22+3×23+···+t×2t,

错位相减,求得S2t+1-1=(t-1)2t+1+2.

从这位学生提出的问题和解答可以看出,该生不但具备了数学思想方法迁移的能力,而且具备了较强的概括能力和抽象水平,数学思维品质得到发展,数学抽象素养得以落实.

4 结束语

“U 型”模式是素养导向的教学模式,是数学抽象素养落地的有效路径. 要注意的是,核心素养水平的达成不是一蹴而就的,数学抽象素养的培养亦是如此,教师要有意识把“U型”教学模式渗透到每一节课,当然不是每节课都只有一个“U 型”过程,可以是多个“U 型”循环,若学习内容不完整,也可以多节课一个“U 型”,学生在经历一个个“U 型”的过程中,核心素养特别是数学抽象素养就潜移默化、润物细无声地得到落实了.