圆柱壳体振动陀螺高精度频率检测方法*

于亚龙，孙小燕，胡友旺

(高性能复杂制造国家重点实验室 中南大学 机电工程学院，湖南 长沙 410083)

0 引 言

圆柱壳体振动陀螺是一种哥式振动陀螺，它利用谐振子振动产生的驻波相对于谐振子本身的滞后效应，且滞后的角度与转速成正比的原理进行工作[1]，具有精度高、能耗低、启动快、抗干扰性好、制造难度低等优点，极具发展潜力[2～6]。由于材料不均匀、加工误差、电极粘贴误差以及谐振子安装误差等的存在，陀螺会产生频率裂解、振型偏移和阻尼分布不均匀等性能不足，进而引起一定的零偏漂移和陀螺灵敏度的降低等问题[7,8]。要提升陀螺的性能，需要通过频率修调工作来降低它的频率裂解。频率裂解降得越低，陀螺的性能越高；而频率裂解需要高精度的检测技术来作为支撑。

英国的通用电气航空电子设备有限公司较早进行了圆柱壳体振动陀螺的研究[9]，但目前在圆柱壳体振动陀螺的研究和制造方面处于领先地位的是Watson公司和Innalabs公司[10,11]。国防科技大学陶溢等人从结构、制造工艺以及振动理论方面对圆柱壳体振动陀螺进行了系统分析，为国内圆柱壳体振动陀螺的研究奠定了基础[1]。此后，谢笛等人通过数字化测控技术实现了对于圆柱壳体振动陀螺的控制[12]，虽然他们的测控技术较为成熟，但都是基于陀螺的整体工作系统的控制,并不是直接应用于频率修调工作，不具有针对性,且系统较为复杂。

针对圆柱壳体陀螺的频率修调工作，本文提出一种基于FPGA、单片机和MFC程序的用于圆柱壳体振动陀螺频率及裂解值的精确检测方法，为频率修调提供重要支撑技术，为圆柱壳体振动陀螺技术发展奠定基础。

1 频率检测整体方案设计

本文采用相位控制技术结合自动增益控制(automatic gain control,AGC)技术的方式使圆柱壳体振动陀螺的谐振子产生自激振动，信号流图如图1所示，其中Ri为谐振子等效电阻，Li为谐振子等效电感，Ci为谐振子等效电容，C0为压电电极的静电容，ni为流控电流源的转移电流比[1]。在信号流图1中，谐振子、压电电极、移相器、AGC、放大器和带通滤波器组成环路，当环路满足自激振荡的条件时，谐振子将产生谐振，其谐振环路输出的信号为正弦信号。

图1 自激振动信号流图

针对谐振子电极的输出信号，本文采用一种基于现场可编程门阵列(field prgrammable gate array,FPGA)和单片机的检测方法。FPGA的时序逻辑能力较强，将其作为信号的频率测量模块，单片机作为控制模块。谐振子电极的输出信号为一正弦波，不能直接接入FPGA的引脚，需要将其通过波形整形转为TTL信号再接入FPGA。FPGA将测得的频率数据通过spi与单片机通信，将数据传输给单片机。单片机对其进行计算得到频率值，并实时显示在液晶屏上，同时通过串口通信将频率值上传给PC端。

2 测频原理

等精度法测频原理是一种测量精度与被测频率无关的测频电路,图2(a)为等精度法的模块图,其中CNT1和CNT2均为可控的多位高速计数器，ENA1和ENA2分别为它们的计数使能端，CLK1和CLK2分别为标准信号fs和被测信号fx的输入端,原理图如图2(b)所示。

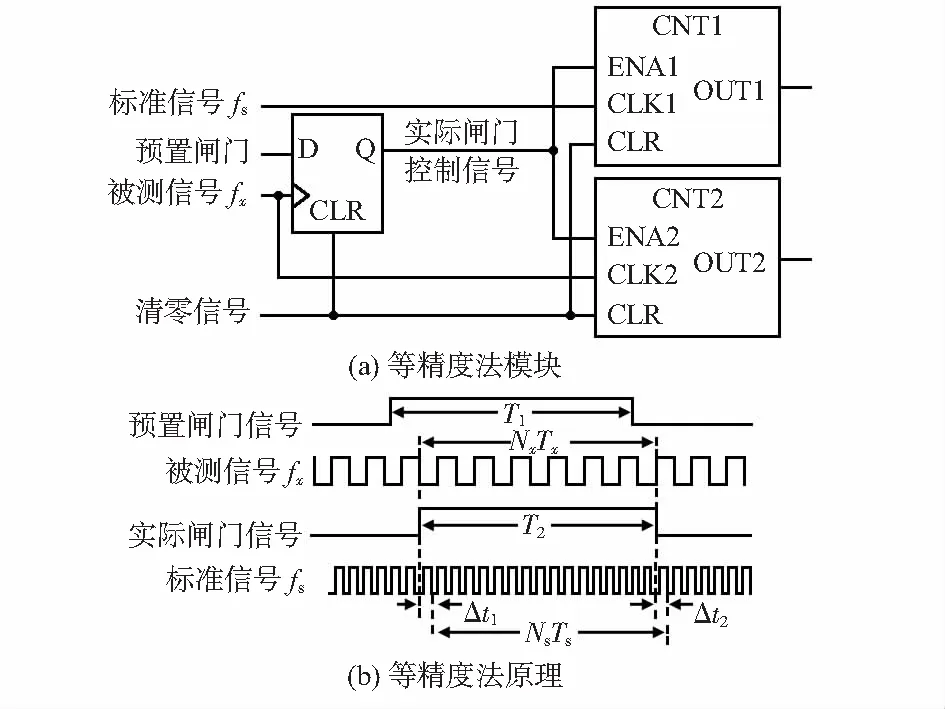
图2 等精度法模块与原理

开始测频前，需要通过清零信号CLR将两个计数器和D触发器清零。在测频未开始时，预置闸门信号处于低电平状态，D触发器的Q端输出低电平，计数器CNT1和CNT2不工作。测频开始时，预置闸门信号上升沿到来，此时计数器并未开始计数，而是等到被测信号的上升沿到来时，D触发器的Q端才变为高电平，2个计数器开始计数。当经过T1秒后，预置闸门信号下降沿到来时，2个计数器并不会马上停止计数，而是等到被测信号的上升沿到来时，才通过D触发器将2个计数器同时关闭，一次测频结束。在测量过程中，因为fx计数的开始和结束时间都是由被测信号自身的上升沿触发的，所以，在闸门开启时间T2内对于被测信号周期数的计数值Nx无误差。若将一次实际闸门时间T2中的被测信号计数值记为Nx，标准频率信号的计数值记为Ns，则有fx/Nx=fs/Ns。鉴于标准频率fs的误差很小，忽略fs误差的情况下，等精度测频的相对误差可表示为[11～15]

(1)

其中,fxe为被测信号频率的准确值。由式(1)可知等精度法测量频率的相对误差只与闸门时间和标准信号的频率有关，而与被测信号的频率大小无关。闸门时间越长，标准频率越高，则被测频率的相对误差越小。

若闸门时间为500 ms,标准信号频率为150 MHz,则相对误差为

(2)

由于等精度测频法与被测信号的频率无关,所以，无论被测信号频率为多少,测量的相对误差均为0.000 001 3%。

3 FPGA和单片机模块设计

3.1 FPGA模块设计

FPGA的总体程序模块原理如图3所示，包含锁相环倍频模块、等精度测频模块、数据锁存模块和spi通信模块。

图3 FPGA模块原理

锁相环倍频模块用于将外部晶振时钟的频率信号进行倍频，以产生更高频率的标准信号来作为系统的时钟。本文FPGA的外接晶振为50 MHz的有源晶振，经过倍频模块的3倍频将产生150 MHz的时钟，该时钟用于整个系统工作的系统时钟。

等精度测频模块主要功能是通过FPGA程序实现上述的等精度测频原理，其主要包括延时消抖模块、待测信号选择模块、闸门时间控制模块和计数模块。当正弦信号通过比较器转换为TTL信号后,信号可能会产生边缘抖动,该抖动信号的频率较高(脉宽较窄),因此可以利用此特性,通过延时来消除信号的抖动。在延时消抖模块中，通过寄存器来实现延时,同时达到消除抖动的目的。闸门时间控制模块主要用于控制闸门的打开时间，而闸门的打开时间直接影响测量的精度，因此，闸门时间控制模块是整个等精度频率测量模块的核心部分。同时，闸门时间控制模块也控制着计数模块计数器的计数进程。计数模块则主要用于测量待测信号和标准信号在闸门时间内的周期个数，并将这些数据传给计数值接口供其他模块使用。

3.2 单片机模块设计

单片机程序流程为：端口初始化，系统时钟初始化，液晶初始化，串口初始化，从FPGA读数据，计算和显示频率，频率值上传。单片机上电之后对端口、系统时钟、串口以及液晶屏进行初始化，然后通过spi从FPGA读取数据，并利用数据计算得到频率值，最后将频率值显示并上传给PC端。单片机从FPGA获取的数据为闸门时间内待测信号的周期数Nx和标准信号的周期数Ns，通过公式fx/Nx=fs/Ns可计算得到待测信号的频率fx，其中,fs为已知的标准信号频率即FPGA的系统时钟频率150 MHz。

4 PC端数据接收与处理程序

频率检测过程中，由于陀螺谐振子所处环境的温度、湿度等因素的变化，其频率值会有一定的波动，进而对频率检测产生影响。为了能够得到更为可靠的数据，并实现数据的存储功能，开发了一种基于C++的MFC程序。该程序的主要功能包括：串口数据接收和转换、数据去干扰、最小二乘处理和数据导出。其流程框图如图4(a)所示。程序开始运行后，从串口读取数据并将其转换为十进制数据，然后判定数据是否为干扰数据，如果是干扰数据则重新读取数据，如果是非干扰数据则进行存储。当数据存储到了120个时，用这120个数据进行最小二乘拟合，判断最小二乘拟合的标准差是否超过设置的标准差极限，如果小于极限值则把最小二乘拟合的频率值进行显示和记录。FPGA每500 ms测一次频率值，那么使用120个数据进行最小二乘拟合可以得到60 s内的稳定频率值，可以降低外部环境对于频率的影响。

程序界面如图4(b)所示，主要包含串口选择、标准差极限设置、实时频率显示区、稳定频率显示区、标准差上限设置区、清除缓存按钮和数据导出按钮。该程序可以实时显示接收到的数据以及最小二乘处理后的稳定频率数据，同时还能将接收的数据导出存储。

图4 MFC程序框图及界面

5 实验结果

等精度测频实验平台由圆柱壳体陀螺、激励电路板、FPGA—单片机模块、信号调理模块、TTL-USB模块等组成。其中，FPGA—单片机模块为集合了FPGA和单片机的功能板，TTL-USB模块起到连接单片机串口和PC端的USB接口的作用。打开直流电源将谐振激励电路上电，谐振子起振，待振动稳定后，打开FPGA—单片机电源。谐振信号从谐振环路引出,经整流模块转换为TTL信号。TTL信号接入FPGA的引脚，FPGA—单片机模块对TTL信号进行频率检测，并将频率值显示在液晶显示屏上，同时将频率数据通过串口经TTL-USB模块上传到PC端。

用上述实验平台分别对陀螺的模态A和模态B进行频率检测，每隔1 min从MFC程序界面读取一次稳定频率数据，每40个数据作为一组。图5为同一陀螺在不同时间检测得到的4组数据的频率变化曲线图，表1为4组数据的统计学分析结果。

图5 陀螺谐振频率数据

表1 频率数据统计学分析 Hz

由表1可知，4组数据的各模态频率的极差最大值为0.002 9 Hz，标准差最大值为0.000 633 Hz，频率裂解值保留3位小数均为0.014 Hz。从频率变化曲线图中可以看出，陀螺的频率值在随着时间波动，但波动范围小于0.002 9 Hz。分析其原因为外部环境的扰动和谐振电路的细微波动而引起的频率波动。因为陀螺频率的细微波动导致不能直接显示每个模态的准确频率值，所以，把每个模态的数据平均值作为该模态的准确频率值，以方便计算，如图5中虚线所示。对于同一模态，在不同时间进行频率检测，其频率数据的平均值不同，但每次测量的2个模态频率值的差值均为0.014 Hz，即4次频率检测的频率裂解值均为0.014 Hz。

6 结 论

根据圆柱壳体振动陀螺的谐振原理，本文搭建驱动环路，得到了稳定的正弦信号，再根据圆柱壳体陀螺的频率范围选择了适合的测频原理，该测频原理的相对误差为0.000 001 3 %。然后通过FPGA、单片机和MFC程序结合的方式对谐振信号进行频率检测，实现了频率值和频率裂解值的稳定精确检测。实验结果表明：本文所提出的检测方法所得频率数据的极差小于0.002 9 Hz而标准差小于0.000 663 Hz，说明数据的波动性小且很稳定，能够精确稳定地测得圆柱壳体振动陀螺的频率值。在不同时间对于同一陀螺检测的频率裂解值均为0.014 Hz，证明本方法可以稳定地检测到10-3Hz量级的频率裂解。综上所述，使用本文所提供的频率检测方法可以精确稳定地检测圆柱壳体振动陀螺的频率值和频率裂解值，可以为圆柱壳体振动陀螺的研究以及频率修调工作提供技术支持。