俯仰机构电动缸推力与俯仰角度关系分析
2022-08-30李汉林
李汉林,陈 君
(中国船舶集团有限公司第八研究院,江苏 扬州 225101)
0 引 言
车载电子设备为满足公路铁路运输条件,通常需将天线阵面倒伏撤收后进行运输,工作时再展开至所需角度。目前阵面展开/撤收执行单元主流采用电动缸和液压缸。电动缸因结构简单、伺服相应迅速等优点而被广泛应用。
倒伏过程中,阵面受力状态随倒伏角度变化而动态变化,电动缸推力也随之变化。分析电动缸推力与俯仰角度之间的关系能更准确地判断电动缸支点选择是否合理,并能确定电动缸主要参数,指导电动缸设计。
本文就某一倒伏机构电动缸推力与俯仰角度之间的关系进行了详细分析。
1 问题描述
某阵面采用电动缸执行倒伏运动,如图1所示,运输时阵面水平布置,工作时翻转到指定角度,相关参数如下:

图1 倒伏机构外形图
(1) 几何参数
阵面重量:500 kg;阵面最大迎风面积:=1.2 m×1 m。
(2) 运动参数
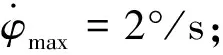
(3) 环境参数:风速=25 m/s。
电动缸额定推力是电动缸设计的重要指标之一,直接决定俯仰机构能否正常工作。故根据上述条件计算出电动缸推力,明确电动缸推力变化趋势,并根据变化趋势推断电缸支点位置是否合理是本机构设计的核心问题之一。
2 计算过程
2.1 电缸力臂与俯仰角关系分析
将上述结构进行简化,俯仰机构运动简图如图2所示。图2中,点为阵面回转点,为电缸支点,是电缸起始位置,是电缸终点位置,是电缸在运动过程中的任意位置,为阵面俯仰角度。

图2 俯仰机构运动简图
在图2中:===1.055 m;=51.5°;=0.879 m;=0.355 m;0°≤≤70°。
令为电缸行程,则:
=+
(1)
根据余弦定律,在Δ中:
=+-2···cos(+)
(2)
将式(1)代入式(2),得:
(+)=+-
2···cos(+)
(3)
由式(3)求得:
=[+-2···
cos(+)]-
(4)
在Δ中,有:
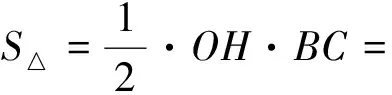
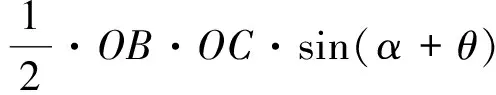
(5)
求得:
=··sin(+)=
··sin(+)(+)
(6)
将式(4)代入式(6),得出电缸对转轴的力臂与阵面转角之间的关系:
==()=··sin(+)/
[+-2···cos(+)]
(7)
2.2 俯仰轴力矩计算
2.2.1 整体分析
对于不在行进中工作的车载设备,一般均为平台调平后进行工作,本阵面亦是如此。故本阵面俯仰过程中,作用在俯仰轴上的力矩主要为重力矩、惯性力矩、风力矩和摩擦力矩。运动过程中,俯仰轴力矩随俯仰角度变化而变化,如都按最大值进行计算,则会导致计算值大于实际推力,导致成本和空间的浪费。俯仰过程中阵面受力状态如图3所示。

图3 阵面受力状态
2.2.2 重力矩
如图3所示,阵面重心绕俯仰轴回转,重力对俯仰轴产生的力矩为:
=··sin(+)=
···sin(+)
(8)
式中:为阵面质量;为重心回转半径;为重心与回转点连线与轴之间的起始夹角。
2.2.3 惯性力矩
理论计算中,阵面相对于俯仰轴的惯性矩为内部各单元相对于俯仰轴的总和,即:
=∑
(9)
随着CAD技术的发展,详细的三维模型能较为精确地反应设备物理属性,可以节省大量的计算时间。根据三维模型计算,本阵面相对于俯仰轴的惯性矩=240 kg·m,则惯性力矩为:

(10)
2.2.4 摩擦力矩
不计电动缸自身产生的摩擦力矩,阵面俯仰过程中摩擦力矩主要来自俯仰轴承,本机构两点支撑,其中一点采用“深沟球轴承+四点接触球轴承”组合形式,另一点采用石墨铜套。
石墨铜套本质为滑动轴承,据相关资料显示,其摩擦系数<0.16。轴承摩擦力矩根据式(11)确定:

(11)
式中:为摩擦系数;为轴承载荷;为轴承内径。
2.2.5 风力矩
经典风力矩计算公式中,风力矩为静态风力矩和动态风力矩之和:
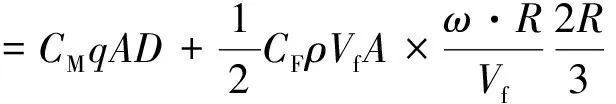
(12)
式中:为设备风阻系数,取经验值,或为某一特定设备在风洞中的实测数据。
设备外观与参照物差异会导致按上述公式计算的理论值与实际值相差较大。随着CAE技术的发展,利用计算机确定的风力矩与实测值相差较小,此方法得到了广泛的应用。
根据式(12)可知,风力矩与迎风面积成正比,阵面俯仰过程中,迎风面积与俯仰角成正弦关系变化,理论上在90°时达到最大值。故利用仿真软件对阵面在90°时对俯仰轴的风力矩进行仿真分析,仿真结果如图4所示。

图4 阵面风力矩仿真
经仿真分析,作用在俯仰轴上的最大风力矩=500 N·m,则任意位置风载荷对俯仰轴的力矩为:
=·sin
(13)
2.2.6 总力矩
作用在俯仰轴上的总力矩为:
=+++
(14)
2.3 电动缸推力计算
结合式(7)、(14)得出电动缸推力与俯仰角度之间的关系:
=()=[···sin(+)+
·sin++]/{··
sin(+)/[+-2··
·cos(+)]}
(15)
将数据代入式(15),取值为:0°≤≤70°,利用数学软件进行求解,得出电缸所需最大推力为7 724 N,电缸推力曲线如图5所示。

图5 电动缸推力曲线
从图5可以看出,电动缸推力随俯仰角度变化趋势较为平稳,近似于线性变化,没有出现推力大小、方向的突变,这对电缸的设计很有利,也间接表明本结构电缸支点的选择较为理想。
3 结束语
本文利用几何原理推导出电动缸力臂与俯仰角度间的数学关系,利用CAD、CAE软件详细分析了阵面在俯仰过程中俯仰轴的受力情况,推导出电动缸推力与俯仰角度之间的数学关系,用数学软件对函数求解,得出推力曲线指导电动缸设计。经实物验证,按此算法确定的电动缸完全满足使用要求。本文对此类结构中电动缸推力计算具有一定的参考意义。
