一种基于数字正交变换的频率估计算法

杨 坡，韩光威

(中国船舶集团有限公司第八研究院，江苏 扬州 225101)

0 引 言

在对周期信号的分析中，频率用来表征信号在某段时间内的大致特征。对于典型的周期信号，正弦信号的频率一般定义为其周期的倒数；而对于非周期信号，虽然没有固定的周期，但是可以通过傅里叶级数将非周期信号转换成多个不同频率正弦信号的加权组合，进而可以通过分析各个不同频率正弦信号的特征得到原信号的总体特征。

频率估计是指通过对获得的信号采样值进行变换以及计算，从而估计出淹没在背景噪声下的信号的频率。信号的频率估计在雷达定位、语音信号处理等领域应用广泛。例如当雷达获取了一段辐射源的信号后，通过对其频率的精确估计，可以大致知晓其飞行特征，甚至可以推算出其速度及距离等信息。

本文提出了一种基于数字正交变换的频率估计算法，该算法首先利用数字正交变换获得解析信号，再利用解析信号的相位信息进行频率估计，突破了传统算法分辨率的限制，算法简单，易于实现。

1 基于数字正交变换的频率估计算法

1.1 Welch算法

1965年，Cooley和Turkey在《计算数学》杂志上提出了快速傅里叶变换(FFT)算法，使得FFT和频谱分析得到了快速发展，周期图的谱估计方法得到了广泛应用；1967年，Welch提出的修正周期图法是工程实践中应用最为广泛的经典谱估计方法，该算法在平均周期图法的基础上进行了改进，可以在保持原算法谱估计性能的同时改善其分辨率。对数据分段处理后分别加窗，再计算平均周期图，此方法改善了因分段数增加给分辨率带来的影响，另外各段可以使用不同的窗函数，这样可以改善由于矩形窗旁瓣较大所产生的谱失真，从而保证得到的谱是渐进无偏的估计。Welch算法步骤如下：

(1) 假设随机信号()有个观察点，则信号的傅里叶变换为：

(1)

(2) 对式(1)进行谱估计可得：

(2)

(3) 把()平均分为段，每段数据长度为点，分别对段数据计算其周期图，段与段之间部分重叠，由此可以得到功率谱表达式为：

(3)

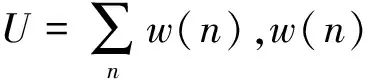
(4) 对式(3)的功率谱进行搜索，找到最大值并记下其索引号，则Welch算法的频率估计为：

(4)

为了较好地估计出功率谱，加窗处理和平均处理都需要同时兼顾减小随机起伏和保证一定的谱分辨率2个方面：由于Welch算法将各段数据进行了重叠处理，从而使得数据段数得到了增加，大大改善了估计的方差，相当于减小了数据的随机起伏，可是各段数据的不相关性也由于数据的重叠而减小，因此估计的方差不会减小到理论的程度。

1.2 基于数字正交变换的频率估计算法

Welch算法是基于功率谱的频率估计，仅仅利用了频谱的幅度信息，而利用相位信息也能提高频率估计精度。

通常接收到的信号往往是实正弦信号的形式，这就需要通过对信号进行正交变换从而得到解析信号和信号的相位信息。最为常用的获得解析信号的方法是数字Hilbert变换，该方法的正交性能由滤波器的阶数决定，通常只有当滤波器的阶数达到上百阶时才能获得较好的滤波性能，这限制了该方法的应用范围。基于数字正交变换的频率估计算法首先利用数字正交变换获得解析信号，再利用解析信号的相位信息进行频率估计，突破了传统算法分辨率的限制，算法简单，易于实现。算法的原理和步骤如下：

(1) 已知一个实信号()，将其解析形式表示为：

(5)

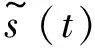
(6)

解析信号与其原信号在频域上的关系为：

(7)

由式(7)可以看出，通过如下方法可得到原信号的解析信号：对原信号作FFT，将双边谱的负频率部分置0，再将正频率部分的频谱扩大2倍，最后求反快速傅里叶变换(IFFT)。这样得到的解析信号避免了对原信号的Hilbert滤波，克服了Hilbert滤波器带来的幅、相不平衡。由于其利用了FFT/IFFT的固有特性，结构规整，运算速度较高，能够满足频率估计的实时性要求。

根据瞬时频率的定义可知，信号的瞬时频率为信号的相位对时间的导数，则信号的频率估计为：

(8)

2 仿真与分析

2.1 目标直线运动

实验参数：目标的初始速度为10 m/s，初始航向为20°(与轴正方向的夹角)；采样率为2 000 Hz，信号频率为284.519 Hz，初相为π/3。目标的运动方式如下：0～100 s作匀速运动；100～110 s作匀加速运动，加速度为0.01 m/s；110 s～200 s作匀速运动。观测数据长度为4 000点。

图1是信噪比为0 dB时Welch算法和基于数字正交变换的频率估计算法对信号频率的跟踪性能；图2和图3是不同信噪比下Welch算法和基于数字正交变换的频率估计算法100次频率估计的均方根误差和估计偏差。

图1 算法对信号频率的跟踪

图2 不同信噪比下的均方根误差

图3 不同信噪比下的估计偏差

2.2 目标曲线运动

实验参数：目标的初始速度为10 m/s，初始航向为20°(与轴正方向的夹角)；采样率为2 000 Hz，信号频率为284.519 Hz，初相为π/3。目标的运动方式如下：0～20 s作匀速运动；20～60 s作匀速圆周运动，半径为800 m；60 s～200 s作匀速运动。观测数据长度为4 000点。

图4是信噪比为0 dB时Welch算法和基于数字正交变换的频率估计算法对信号频率的跟踪性能；图5和图6是不同信噪比下Welch算法和基于数字正交变换的频率估计算法100次频率估计的均方根误差和估计偏差。

图4 算法对信号频率的跟踪

图5 不同信噪比下的均方根误差

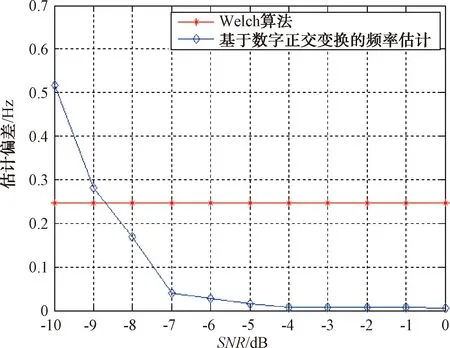
图6 不同信噪比下的估计偏差

由图1和图4可以看出，在一定的信噪比下，基于数字正交变换的频率估计算法能够较好地跟踪信号频率，同时突破了Welch算法的频率分辨率的限制；由图2、图3、图5和图6可以看出，在信噪比为-7 dB～0 dB时，基于数字正交变换的频率估计算法性能好于Welch算法，且该算法不需要频率的粗略估计，实现较为方便，当信噪比低于-7 dB时，算法的估计精度不及Welch算法，且随信噪比的降低性能急剧下降。

3 结束语

分析比较了Welch算法和基于数字正交变换的频率估计算法，前者是基于功率谱的频率估计算法，后者是基于相位信息的频率估计算法。仿真表明，相位差法估计精度较高，但稳定性相对较差；基于数字正交变换的频率估计算法在信噪比较高时表现优异，且算法实现最为简单，并且算法突破了频率分辨率的限制。