关于2022 届佛山市二模第20 题的解法探究

广东省佛山市教育局教研室(528000) 彭海燕

佛山市顺德区罗定邦中学(528300) 龙 宇

在解答立体几何问题时,都可通过向量法以及几何法进行求解. 学生在求解的过程中首先要学会识别图形,明确题目要求. 当用几何法求解时,需结合线面间的位置关系以及空间角的定义作出相关图形;当利用向量法求解时则需要进行适当地转化,将空间关系转化为向量间的运算,两种方法都体现了学生空间想象能力,是考察学生直观想象核心素养的主要载体. 作为一道优质的立体几何试题,必须要图形结构清晰,选择恰当地条件作为推理的逻辑基础. 其次则是可通过多角度进行运算,让擅长不同方法的学生都可进行求解.2022 届佛二模第20 题就是一道优质的立体几何解答题,该问题入口宽、起点低,立意深远,也为后续的高三备考指明的方向. 笔者在研究过程中,深深地被命题者的巧思所折服,现将探究的过程整理如下,以飨读者.

1. 题目及分析

图1

(1)求证: ΔPAD为直角三角形;

(2)若AD=PB,求直线PD与平面PBC所成角的正弦值.

2. 解法呈现

解法一(向量法1: 构建坐标系求解)如图2,以点P为原点,PB为x轴,PA为y轴,过点P作平面PAB的垂线为z轴建立空间直角坐标系.

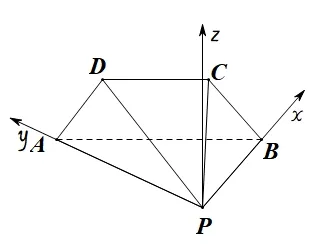
图2

评析 利用空间向量基本定理,避免了建系以及点的坐标等运算,弱化了对空间能力的要求,加强了对代数运算方

解法四(几何法2)在图3 中,过点D作PE的垂线,垂足为M,利用三垂线定理可得DM⊥平面PEB. 可知DM的值即为点D到平面PBC的距离,同时可得∠DPE为直线PD与平面PBC所成角,具体如图4.

图3

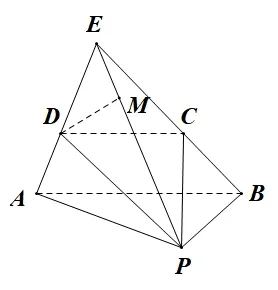
图4

解法六(几何法4: 三面角[1]模型)如图6,三面角是由具有公共端点的不共面的三条射线,以及任两条射线所成的角的内部构成的空间图形. 公共端点称为三面角的顶点,射线称为三面角的棱,两棱所夹的平面部分(角)称为三面角的面(角). 过每一条棱的两个面所成的二面角称为三面角的二面角.

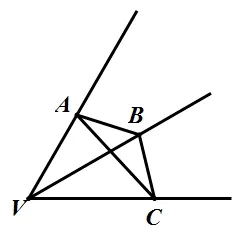
图6

设射线V A与平面V BC所成角为θ,记∠AV C,∠AV B分别为β,γ,记二面角A-V C-B,二面角A-V B-C分别为C,B. 则可得sinθ=sinβ·sinC或sinθ=sinγ·sinB成立,证明过程请看下文.

在图5 中, 考虑三面角P-DEB, 设直线PD与平面PBC所成角θ,设二面角D-PE-B为E,利用上述结论可得sinθ=sin ∠DPE·sinE.

图5

3. 模型分析及推广

在上述求解过程中, 分别从不同的视角解决了该问题.特别地,在解法五及解法六中还总结出了两个一般化的结论.现描述如下:

结论1 在三棱锥P-ABC中,设直线PC与平面ABC和平面PAB所成角分别为:α,β, 则有SΔABC ·sinα=SΔP AB ·sinβ.

利用等体积法即可证明,过程从略.

结论2 在三面角V-ABC中,射线V A与平面V BC所成的角为θ, 记∠AV C,∠AV B分别为β,γ, 记二面角A-V C-B, 二面角A-V B-C分别为C,B, 则可得:sinθ=sinβ·sinC或: sinθ=sinγ·sinB.

证明 如图7,过点A作平面V BC的垂线,垂足为O,连接V O. 过点O作V C的垂线,垂足为C,连接AC,则可得∠AV O为射线V A与平面V BC所成的角.

图7

根据三垂线定理可得:V C⊥AC,则可得∠ACO为二面角A-V C-O的平面角,根据三面角中的标记方法记该角为∠C.

在不同的三角形中,