圆锥曲线中一类定值问题的简证和拓广

深圳市龙华区教育科学研究院附属外国语学校(518109) 钟文体

文[1]用较长的篇幅证明了圆锥曲线的如下三个定值性质(表述略作改动):

命题1 设G为平面有限点集Ω ={A1,A2,··· ,An}的重心, 则以G为中心的椭圆(双曲线) 上任意一点到A1,A2,··· ,An距离的平方和与该点到椭圆的两焦点距离的乘积的n倍之和(差)为定值.

命题2 设G为平面有限点集Ω={A1,A2,··· ,An}的重心,则以G为焦点的抛物线上任意一点到A1,A2,··· ,An距离的平方和与该点到其准线距离的平方的n倍之差为定值.

以上性质是圆的相应定值性质的推广. 本文将用较简单的方法证明上述性质并对结论作一些拓展.

一、问题简证

方法二 设椭圆离心率为e,椭圆上任意一点P的坐标为(x0,y0),则

二、逆命题

本节证明上述各命题的逆命题. 为此,先证明以下引理.

引理3 (三角形中线长公式)设三角形ABC的边BC的中点为D,则AB2+AC2=2AD2+2BD2.

证明 用向量法可简洁地证明此引理. 如图1,

图1

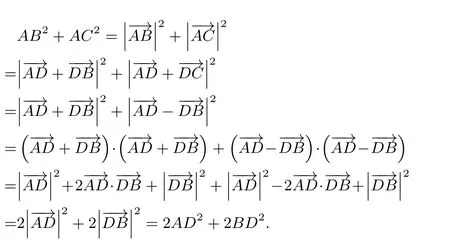
引理4 设F1和F2为平面上不同两点,O为F1F2的中点. 动点P(不在线段F1F2上)到点O距离的平方与该点到点F1和F2距离的乘积之和为定值K,则点P的轨迹是以F1和F2为焦点的椭圆.

证明 以O为坐标原点, 直线F1F2为x轴建立平面直角坐标系. 设F1(-c,0),F2(c,0),P(x,y). 由条件可知PO2+PF1·PF2=K,则

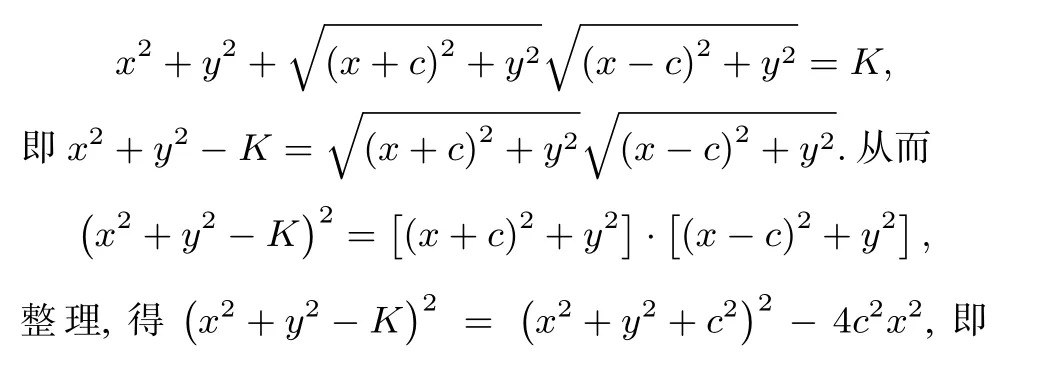
引理5 设F1和F2为平面上不同两点,O为F1F2的中点. 动点P(不在线段F1F2的垂直平分线上,也不在从直线F1F2挖去线段F1F2得到的两条射线上)到点O距离的平方与该点到点F1和F2距离的乘积之差为定值K,则点P的轨迹是以F1和F2为焦点的双曲线.

证明 以O为坐标原点, 直线F1F2为x轴建立平面直角坐标系. 设F1(-c,0),F2(c,0),P(x,y). 由条件可知PO2-PF1·PF2=K,则

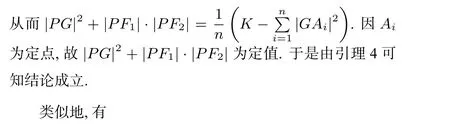
命题5 设G为平面有限点集Ω ={A1,A2,··· ,An}的重心,线段F1F2的中点为G. 动点P(不在线段F1F2的垂直平分线上,也不在直线F1F2挖去线段F1F2得到的两条射线上)到A1,A2,··· ,An距离的平方和与该点到F1和F2距离的乘积的n倍之差为定值K,则点P的轨迹是以F1和F2为焦点的双曲线.

以下考虑命题2 和命题3 的逆命题.

引理6 给定直线l和直线外一点O. 动点P到点O的距离的平方与该点到直线l的距离的平方的λ(λ ＞0)倍之差为定值K. 则点P的轨迹是圆锥曲线. 当λ ＜1 时,轨迹为椭圆;当λ= 1 时,轨迹为抛物线;当λ ＞1 时,轨迹为双曲线.

证明 以O为坐标原点建立平面直角坐标系, 使得直线l与x轴垂直. 设直线l的方程为x=m, 点P坐标为(x,y), 则x2+y2-λ(x-m)2=K, 化简得(1-λ)x2+y2+2λmx=K+λm2,故引理成立.

命题6 设G为平面有限点集Ω ={A1,A2,··· ,An}的重心,l是不经过G的定直线. 动点P到A1,A2,··· ,An距离的平方和与该点到直线l的距离的平方的nλ(λ ＞0)倍之差为定值K. 则点P的轨迹是圆锥曲线. 当λ ＜1 时,轨迹为椭圆;当λ= 1 时,轨迹为抛物线;当λ ＞1 时,轨迹为双曲线.