上海市高考中的绝对值问题

华东师范大学第二附属中学(201203) 戴中元

上海高考中有许多有趣的绝对值问题,如2020 年的压轴题,它们和函数、数列的单调性密切相关. 解决绝对值问题最基本的方法是根据绝对值内函数的零点来进行分情况讨论,但有时也可以先将绝对值符号打开,然后填上正负号来处理. 本文就以笔者在2020 年命制的两道上海市浦东新区高考模拟题为例,来分析解决这类绝对值问题的思路和方法,并将这种方法用于解答向量中的绝对值问题.

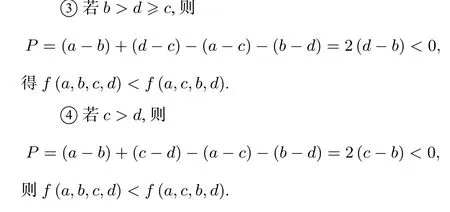
解法2 利用绝对值不等式,由作差法可知f(a,b,c,d)-f(a,c,b,d) =|a-b| +|c-d|-|a-c|-|b-d|, 由a ＞b ＞c或a ＜b ＜c, 知|a-b|-|a-c| =-|b-c|, 故|c-d|-|b-d|≤|b-c|,所以f(a,b,c,d)-f(a,c,b,d)≤0,即f(a,b,c,d)≤f(a,c,b,d). 并且当b ＞c时,d≥b可以取等号,当c ＞b时,若d≤b可以取等号,所以等号可以取到.

(3)分析: 若求波动强度的最小值,设其中最大项为ai,最小项为aj,不妨设i ＜j,则

f(a1,a2,··· ,an)

=|a1-a2|+|a2-a3|+···+|an-1-an|

≥|ai-ai+1|+|ai+1-ai+2|+···+|aj-1-aj|

≥|(ai-ai+1)+(ai+1-ai+2)+···+(aj-1-aj)|

=|ai-aj|=ai-aj,

由不等式取等条件可知当数列{an}从小到大或从大到小排列时波动强度最小,此时的波动强度为最大值减去最小值.

如果要求波动强度的最大值,根据(2)的结论可知若有相邻三项成单调数列,那么可以调整其中两项的顺序(可以从左向右调整,也可以从右向左调整),此时波动强度不会减小, 最终可以调整为任意相邻三项都不是单调数列的情况,要求波动强度的最大值只需考虑这样的数列. 例如1,3,4,2可以调整为1,4,3,2,再调整为1,4,2,3,如图1.

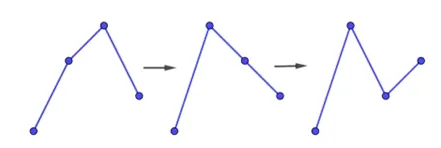
图1

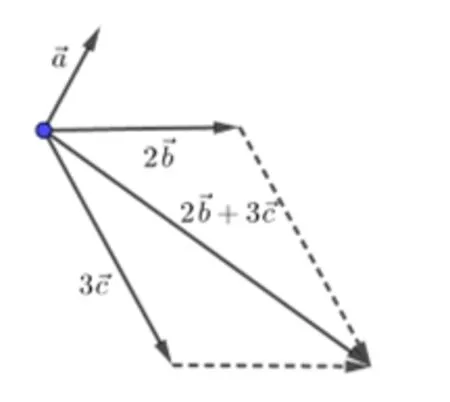
图2

分析 因为内积的结果是实数, 所以式子|a·e| +2|b·e| + 3|c·e| 中的“||”符号是绝对值, 所以可以将|a·e| + 2|b·e| + 3|c·e| 的绝对值符号去掉, 添上±, 变为±a·e±2b·e±3c·e,原式的取值便是这8 种情况中的1种,要求±a·e±2b·e±3c·e=(±a±2b±3c)·e的最大值,也就是要求|±a±2b±3c|的最大值,而|a+2b-3c|=|-a-2b+3c|,所以8 种情况本质上只有4 种,所以只需求出|±a±2b+3c|的最大值.