双输入面齿轮分流-并车传动系统固有特性分析

莫帅，宋裕玲，冯志友，宋文浩，岑国建，黄云生

(1. 广西大学机械工程学院，广西 南宁，530004；2. 天津工业大学机械工程学院，天津，300387；3. 江苏万基传动科技有限公司，江苏 泰州，225400；4. 宁波中大力德智能传动股份有限公司，浙江 宁波，315301；5. 深圳市合发齿轮机械有限公司，广东 深圳，518100)

高性能航空旋翼机齿轮传动系统对于提升整个装备的负载能力和动力传输速度具有重要意义。经研究发现，面齿轮在传动领域较传统齿轮具有更大的潜在优势，其不受径向力的作用，对轴向误差不敏感，传动容差能力强，具有极其广阔的应用前景。此外，面齿轮和直齿轮的配合可以实现动力分流和换向，具有稳定的高减速比。针对高性能航空旋翼机传动系统重大型号需求，国外学者提出了一种航空双输入面齿轮分流-并车传动系统构型，以进一步提高旋翼机的性能和负载能力，该构型具有功率密度高、承载能力强、振动噪声小、服役寿命长等优点。本文以该系统为研究对象，对其固有特性进行研究。

近年来，国内外学者对齿轮系统的固有振动特性进行了深入研究。许华超等[1]建立了柔性直齿内齿圈的振动分析模型，归纳总结了其振动模式。靳广虎等[2]获得了影响一种新型的面齿轮和圆柱齿轮组合传动系统负载分配的敏感性参数。莫帅等[3]采用集中参数理论建立了面齿轮-行星传动串联系统的动力学模型，并对该系统的固有频率进行求解。TAN等[4]研究了考虑电磁刚度的双馈风力涡轮机传动系统的模态形状、模态能量和幅频响应。DONG等[5]研究了飞机用面齿轮双动力分流传动系统的动态均载性能，找出了影响最大的因素。张俊等[6]考虑了内齿圈柔性，建立了行星齿轮传动刚柔耦合动力学模型，并对其自由振动特性进行了理论分析。宋轶民等[7]通过计算得到了经典的3K-II型直齿行星齿轮传动系统的固有频率和振型。MO 等[8-9]建立了双螺旋星形齿轮系统和人字齿轮行星系统精细的动力学模型，并利用该模型对振动和固有特性进行分析。李同杰等[10]在考虑滑动轴承因素基础上，运用数值分析法研究了齿轮副啮合冲击特性的变化规律。张栋林等[11]分析了共轴对转封闭差动轮系中固有频率对刚度和质量的参数灵敏度以及频率变化轨迹中的模态跃迁现象。满维伟等[12]运用数值方法得到了齿轮副的动态传动误差和振动加速度等振动响应。XIAO等[13]揭示了应用在月球采样器上的行星齿轮系统的固有振动特性。YAN 等[14]对两级直齿锥齿轮传动系统的非线性振动响应进行了理论分析，并对具有陀螺效应的传动系统的固有频率、模态振型和临界转速进行计算。魏静等[15]将实验条件更新为飞行状态下非惯性环境，探究了各构件的动力学行为。WANG 等[16]构建了考虑多种因素的齿轮传动涡扇发动机变速箱的非线性动力学模型，并研究了其动态响应特性。刘利等[17]揭示了系统刚度变化对固有频率的影响规律以及固有频率变化过程中的模态跃迁现象。LIU等[18]研究了在不同力矩和速度条件下柔性支撑对行星齿轮系统振动的影响。

从已有文献来看，国内外学者对传动系统的动力学特性研究主要集中于经典行星和星型齿轮传动，对包含混交面齿轮系统的分析甚少。为此，本文作者以一种新型的双输入面齿轮分流-并车传动系统为研究对象，建立其动力学模型和运动微分方程，并对系统的固有频率和模态能进行分析。

1 动力学模型

图1 所示为双输入面齿轮分流-并车传动系统构型。该系统为新型复杂齿轮传动，结合了面齿轮和直齿轮的优点，由2 个输入级、4 个分扭级和2 个并车级齿轮副组成，左右对称。2 台发动机动力分两路独立传递到圆柱齿轮上并成一定夹角分支传动，输入圆柱齿轮同时与正交面齿轮和非正交面齿轮耦合啮合实现“一拖二”输入端分流传动，分为左右两支动力输入端。同正交面齿轮和非正交面齿轮同轴相连的上分支圆柱齿轮同时分流至与其啮合的下分支圆柱齿轮，上下两层各4个直齿轮将四支动力汇流合并到大面齿轮上实现“四合一”输出端汇流并车传动，最后所有动力汇流经大面齿轮输出到与其连接的螺旋桨。同时，各传动级齿轮之间由分扭轴或双联轴连接固定。分扭轴上连接有面齿轮、分流主动轮和上直齿轮，双联轴的一端是分流从动轮，另一端是下直齿轮。

图1 双输入面齿轮分流-并车传动系统Fig.1 Double input face gear split-parallel transmission system

图2所示为基于集中参数法建立的双输入面齿轮分流-并车传动系统简易动力学模型。图2 中，T0为输入扭矩；T1为输出扭矩。K，C和e分别为刚度、阻尼和啮合误差，其对应的下标含义如下：u 表示大面齿轮；si表示第i个与大面齿轮啮合的上直齿轮；hi表示第i个与大面齿轮啮合的下直齿轮；sj表示输入齿轮；lj表示输入级的正交面齿轮；pj表示非正交面齿轮；gk_j表示主动轮齿轮副，qk_j表示从动轮齿轮副；对于连接轴，支撑lj，g1_j和si的轴命名为分扭轴Ⅰ；支撑pj，g2_j和si的轴命名为分扭轴Ⅱ；支撑q1_j和hi的轴命名为双联轴Ⅰ；支撑q2_j和hi的轴命名为双联轴Ⅱ。其中，i=1，2，3，4；k=1，2；j=L，R；L表示左侧部分的构件，R表示右侧部分的构件。通过分析各齿轮的运动规律和自由度，得到系统的广义位移矩阵X为

图2 双输入面齿轮分流-并车传动系统简易动力学模型Fig.2 Simplified dynamic model of the double input face gear split-parallel transmission system

式中：x，y和z分别为每个齿轮沿相应坐标轴的位移；θ为扭转角位移。

在动力学模型中，圆柱齿轮和输入级正交面齿轮有3 个自由度，大面齿轮和非正交面齿轮有4个自由度，同时为每个齿轮建立坐标系，其中，在大面齿轮理想中心处建立固定坐标系OuXuYuZu，O1X1Y1Z1为建立于传动系统左分扭轴Ⅱ和左双联轴Ⅱ上的齿轮坐标系，O4X4Y4Z4为建立于右分扭轴Ⅱ和右双联轴Ⅱ上的齿轮坐标系，O2X2Y2Z22为建立于左分扭轴Ⅰ和左双联轴Ⅰ上的齿轮坐标系，O3X3Y3Z3为右分扭轴Ⅰ和右双联轴Ⅰ上的齿轮坐标系。在此系统中，分扭级各齿轮坐标系设置相同，上、下并车级各直齿轮坐标系在大面齿轮固定坐标系中存在位置角，定义为Asi和Ahi，沿逆时针排列，依据各个齿轮在坐标轴上的振动位移进行运动微分方程的建立和求解。

2 动力学方程

2.1 相对位移

分扭级圆柱齿轮副的动力学模型描述了处于啮合状态的齿轮副的受力情况和相对位置关系，如图3所示。图4所示为并车级和输入级齿轮副啮合力的相互作用关系。根据理论分析可知，在齿轮啮合过程中，齿轮副在啮合点处会因振动位移和误差产生微位移，在计算齿轮副的啮合力和啮合阻尼力时，需要将每个齿轮的微位移投影到啮合线上，以获得齿轮副相对位移。

图3 分扭级圆柱齿轮副动力学模型Fig.3 Dynamic model of cylindrical gear pair of the spilttorque stage

图4 面齿轮副啮合力的相互作用Fig.4 Interaction relationship of the meshing forces of the face gear pairs

此系统中，上、下并车级各齿轮副的相对位移δusi和δuhi分别为：

输入级各齿轮副的相对位移δslj和δspj分别为：

分扭级齿轮副的相对位移δgqk_j为

式中：rbsi，rbhi和rbsj分别为并车级上直齿轮、并车级下直齿轮和输入齿轮的分度圆半径；ru，rlj和rpj分别为大面齿轮、正交面齿轮和非正交面齿轮啮合齿面间的法向动载荷与转动中心之间的距离；αus，αuh，αls，αps和αgqk分别为大面齿轮和上直齿轮、大面齿轮和下直齿轮、正交面齿轮和输入齿轮、非正交面齿轮和输入齿轮，分流齿轮副的压力角；eusi，euhi，elsj，epsj和egqk_j分别为大面齿轮和上直齿轮、大面齿轮和下直齿轮、正交面齿轮和输入齿轮、非正交面齿轮和输入齿轮以及分流齿轮副的综合传递误差。

在齿轮的加工和装配过程中不可避免地存在误差，如基节偏差、齿形误差和偏心误差等，用近似的简谐函数对总的综合传递误差进行模拟，其表达式为

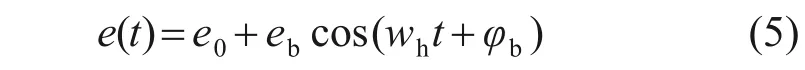
式中：e0为齿轮副综合传递误差；eb为综合传递误差变化幅值；wh为啮合频率；φb为初始相位角。

根据受力分析，结合相对位移可以得到该传动系统中齿轮之间的啮合力F和啮合阻尼力D：

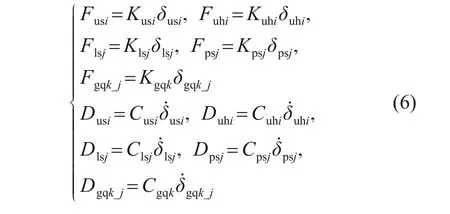
式中：Kusi，Kuhi，Klsj，Kpsj和Kgqk_j分别为大面齿轮和上直齿轮、大面齿轮和下直齿轮、正交面齿轮和输入齿轮、非正交面齿轮和输入齿轮、分流齿轮副之间的啮合刚度；Cusi，Cuhi，Csj，Cpsj和Cgqk_j分别为大面齿轮和上直齿轮、大面齿轮和下直齿轮、正交面齿轮和输入齿轮、非正交面齿轮和输入齿轮、分流齿轮副之间的啮合阻尼。

2.2 动力学方程

分析各构件的受力情况，依据牛顿第二定律建立各齿轮的运动微分方程(式(7)～式(14))，其中，m为质量；J为转动惯量；T0和T1分别为作用于输入齿轮和大面齿轮上的输入扭矩和输出扭矩。

大面齿轮的运动微分方程为

上直齿轮的运动微分方程为

下直齿轮的运动微分方程为

输入齿轮的运动微分方程为

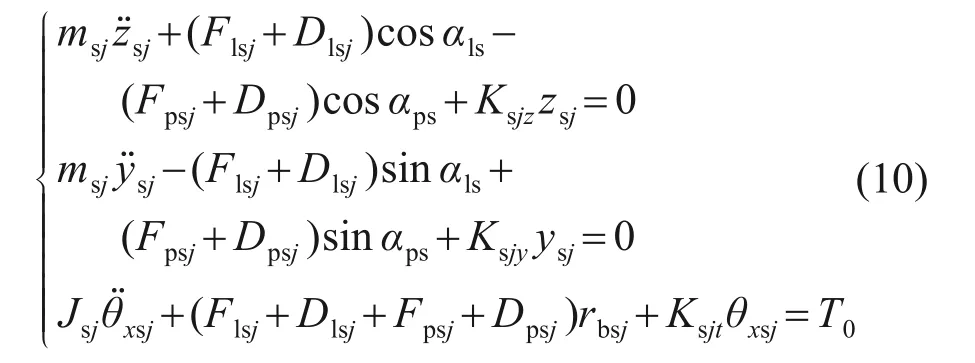
正交面齿轮的运动微分方程为

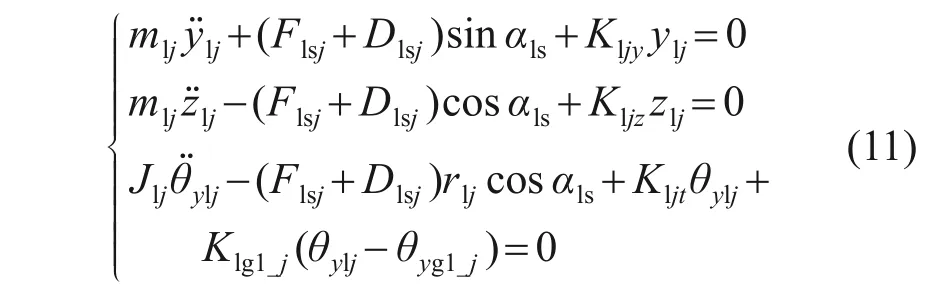
非正交面齿轮的运动微分方程为

分流齿轮副中主动轮的运动微分方程为

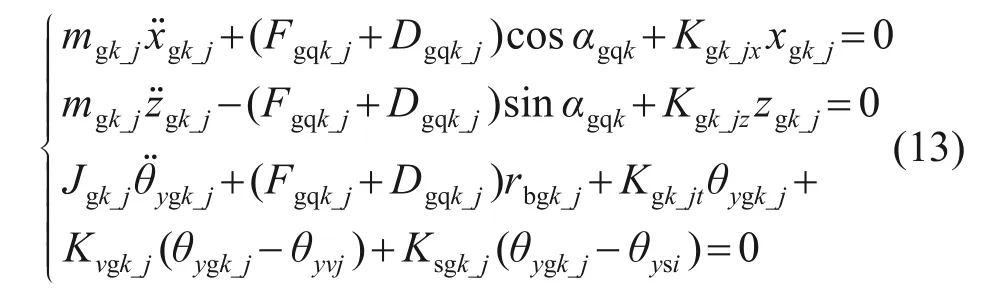
分流齿轮副中从动轮的运动微分方程为

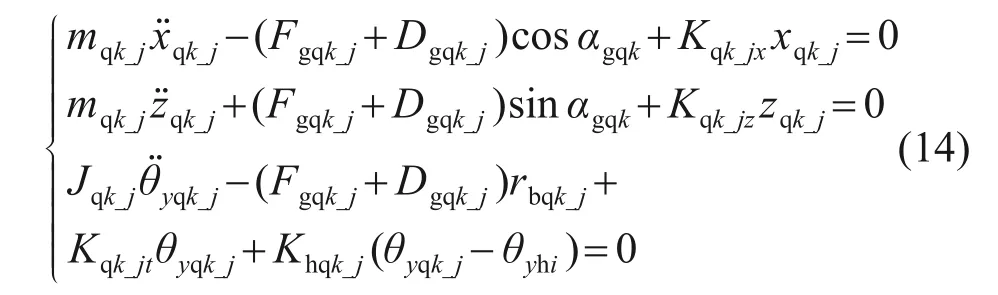
式中：Ksgk_j为分扭轴中连接并车级上直齿轮和分流主动轮段的扭转刚度；Khqk_j为双联轴的扭转刚度；Kvgk_j为分扭轴连接输入级面齿轮和分流主动轮段的扭转刚度，其中，v=l，p，分别表示正交面齿轮和非正交面齿轮。

3 固有特性分析

3.1 固有频率求解

通过求解动力学方程的特征值，即可获得系统的各阶固有频率和相应振型。采用表1所示技术参数设计传动系统，并对其固有特性进行研究。

表1 传动系统技术参数Table 1 Technical parameters of the transmission system

固有频率是系统固有特性的反映，只由系统本身决定。忽略惯性力以及内外激励，利用运动方程可以得到系统简化的无阻尼自由振动方程以及特征值方程，从而对系统的振动模态进行分析：

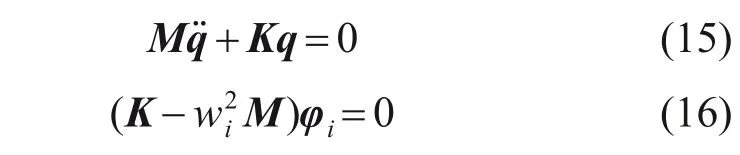
式中：M为质量矩阵；q为系统广义位移矩阵；K为刚度矩阵；wi为第i阶固有圆频率，对应固有频率fi(fi=wi/2π)；φi为对应的振型矢量(i=1，2，…，72)。传动系统的各阶固有频率和重根数见表2。

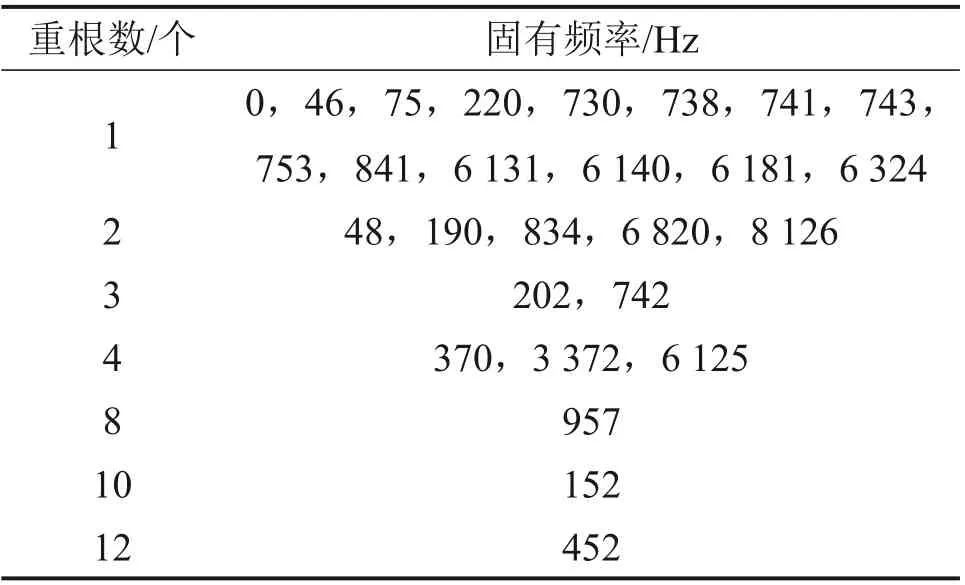
表2 传动系统的各阶固有频率和重根数Table 2 The natural frequencies and number of multiple roots of the transmission system

振动模式可以反映各构件的振动情况，有利于分析系统的动态特性。根据系统特征值的重根数，将对应的振型矢量进行分类，可以得到系统的振动模式。经过归纳总结，发现所研究的双输入面齿轮分流-并车传动系统包含多个振型，在7种重根对应的72 阶固有频率中，每一传动级齿轮均存在独特的平移振动模式和扭转振动模式，如与固有频率452 Hz(12重根)对应的振型矢量中，系统表现为分扭级直齿轮绕中心轴线作扭转振动，其他齿轮无位移，故可定义为分扭级直齿轮扭转振动模式；与固有频率152 Hz(10重根)对应的振型矢量中，存在2种振动模式，即输入级面齿轮平移振动模式和分扭级直齿轮扭转振动模式；与固有频率957 Hz(8 重根)对应的振型矢量中，振动模式为并车级直齿轮平移振动模式；而在重根数相同的固有频率对应的振型矢量中，多种振动模式并存。

3.2 模态能分析

3.2.1 模态应变能

模态应变能反映了齿轮变形程度，包括啮合应变能、支撑应变能以及扭转应变能。因大面齿轮的质量和尺寸比其他齿轮的大，其应变能和动能也较大，故忽略其模态能。

齿轮径向平移振动产生的支撑应变能Uf为

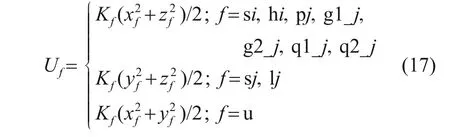
齿轮轴向平移振动产生的支撑应变能Ufz为

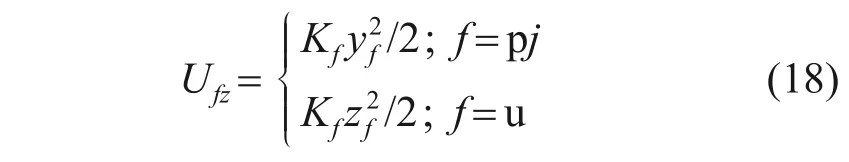
齿轮扭转振动产生的扭转应变能Ufθ为

齿轮啮合变形引起的啮合应变能Uij为

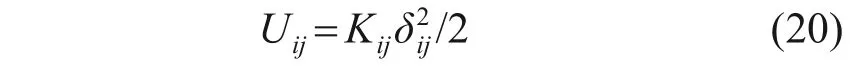
式中：Kij为各齿轮副的啮合刚度；δij为各齿轮副的相对位移。

由式(17)～式(20)可以得到整个传动系统在第i阶模态的应变能Ui为

双输入面齿轮分流-并车传动系统中各阶固有频率下的模态应变能分布状态见图5。从图5(a)可见：第46 阶固有频率对应的啮合应变能Uu_h2和Uu_h3是所有啮合应变能中最高的。从图5(b)可见：除大面齿轮外，其余齿轮第12 阶固有频率对应的径向支撑应变能UpL是所有平移振动应变能中最高的，这说明并车级啮合刚度Ku_h2，Ku_h3对第46 阶固有频率影响最大，左非正交面齿轮径向支撑刚度KpL对第12阶固有频率影响最大。传动系统中产生轴向平移振动的是大面齿轮和非正交面齿轮。由图5(c)可见：左、右非正交面齿轮的轴向支撑应变能在第3～15 阶固有频率中变化，且轨迹相似。由图5(d)可见：系统正常运行过程中，第46 阶频率下的总应变能最大，此时系统整体变形最大。

图5 系统模态应变能Fig.5 Modal strain energy of the system

3.2.2 模态动能

模态动能反映的是齿轮振动的剧烈程度，由平移动能和扭转动能构成。

齿轮径向平移振动产生的动能Ef为

齿轮轴向平移振动产生的动能Efz为

齿轮扭转振动产生的动能Efθ为

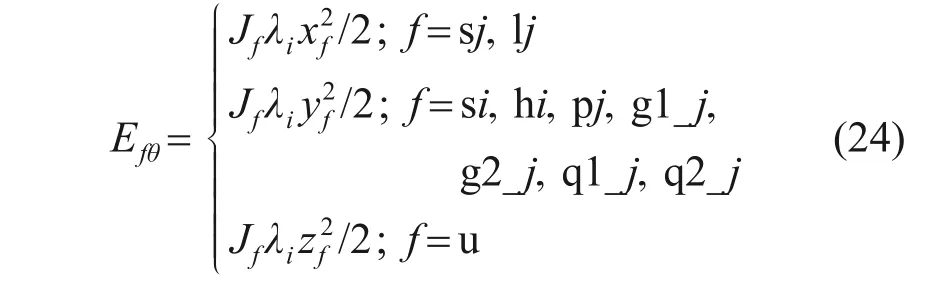
由式(22)～式(24)可以得到整个传动系统在第i阶模态的动能Ei为

图6所示为系统模态动能在各阶固有频率下的分布状态。从图6(a)可见：第72 阶频率下的输入齿轮扭转动能最大，此时扭转振动最剧烈。从图6(b)可见：第69 阶频率下的输入齿轮平移振动最剧烈，这说明输入齿轮的质量对第69 阶固有频率影响最大，转动惯量对第72 阶固有频率影响最大。从图6(c)可见：左、右非正交面齿轮的轴向平移动能均在第3～15 阶固有频率中变化，且轨迹相似。从图6(d)可见：在系统正常运行过程中，第60阶频率下的总动能最大，此时系统振动最为剧烈。

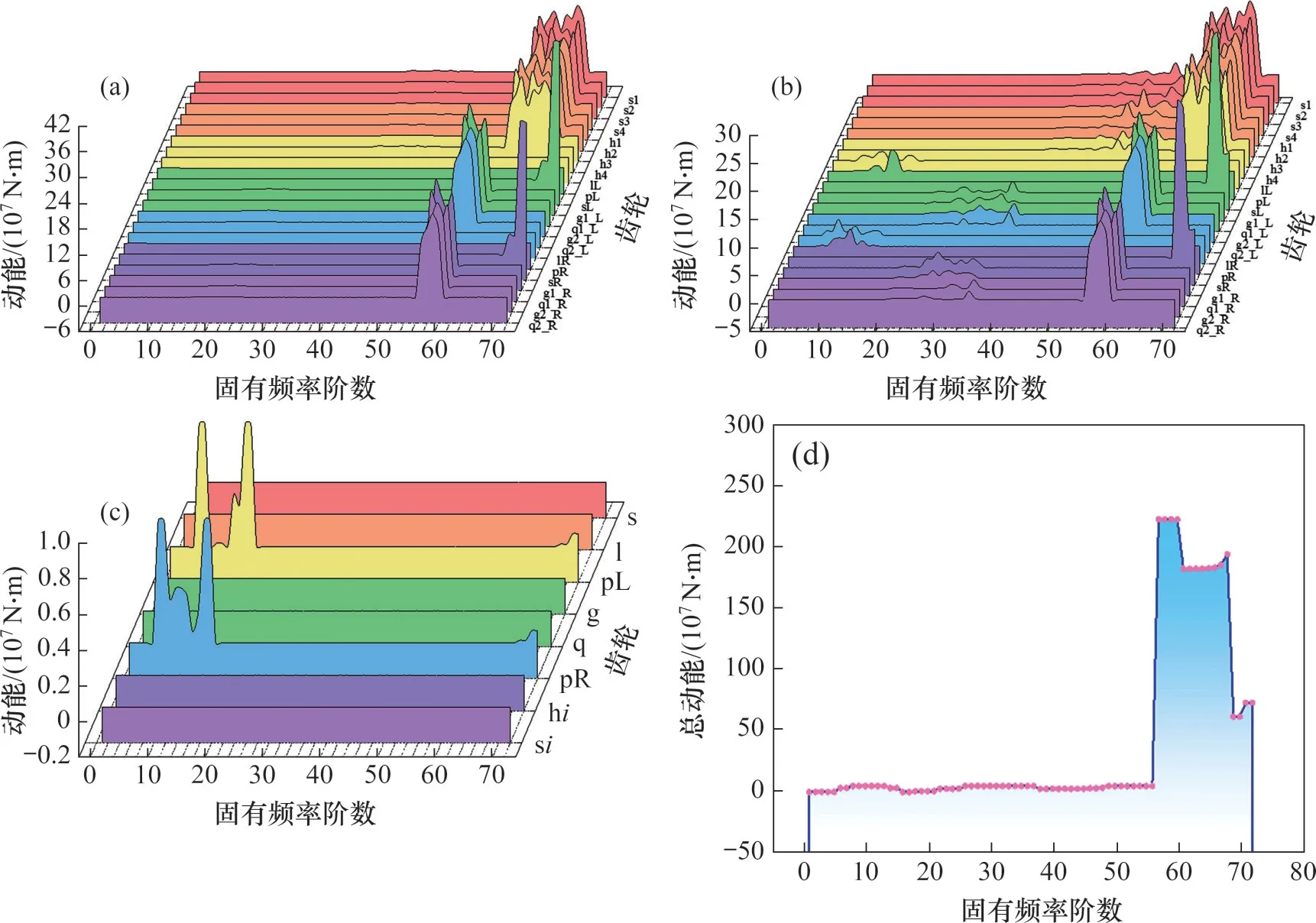
图6 系统模态动能Fig.6 Modal kinetic energy of the system

4 系统刚度对固有频率的影响

4.1 啮合刚度对固有频率的影响

保证系统中其他参数不变，若改变各齿轮副的啮合刚度，则系统的固有频率随之变化，结果如图7 所示。由图7(a)和图7(b)可见：输入级正交面齿轮副和非正交面齿轮副啮合刚度和固有频率的关系曲线变化规律相似。随着啮合刚度逐渐增大，第61阶和62阶的固有频率先是不断增大，然后基本不再发生变化；第68～70阶的固有频率则先是基本不变，然后不断增大，增大到一定程度后不再发生变化；第71阶和72阶的固有频率始终呈现出上升的趋势。

由图7(c)可见：随着啮合刚度从1×109N/m 逐渐增加到1×1010N/m，第59 阶和60 阶的固有频率先是不断增大，然后不再发生变化；第66～72阶的固有频率则先是基本不变，然后不断增大，增大到一定程度后不再发生变化，其中频率阶次越高，前期固有频率保持不变的时间越长，后期增幅也越大。由图7(d)可见：第61～64阶固有频率只在初始变化时有小幅增加，之后便保持不变；第65～68阶的固有频率持续增大，且变化明显；第69～72阶的固有频率先是不变，后逐渐增大。由图7 可知：传动系统的各齿轮副啮合刚度主要对高阶固有频率有影响，使其增大，对低阶固有频率无影响。

图7 齿轮副啮合刚度对固有频率的影响Fig.7 Influences of gear meshing stiffness on the natural frequencies of the system

4.2 支撑刚度对固有频率的影响

系统中传动轴支撑刚度对固有频率的影响如图8 所示。设置支撑刚度从1×108N/m 增加到1×1010N/m，由图8可以发现分扭轴Ⅰ和Ⅱ以及双联轴Ⅰ和Ⅱ的支撑刚度对固有频率的影响均相似，即低阶频率基本无变化，中高阶频率随之增大而增加。

低阶固有频率在支撑刚度初始变化时有小幅增大，之后便保持不变；在中高阶频率中，随着支撑刚度增大，第49～50和53～58阶的固有频率持续增大，且变化范围相当；第51和52阶的固有频率先逐渐增加，后保持不变，整体变化不大；第61和64阶的固有频率基本无变化；第65和66阶的固有频率先基本不变，然后不断增大，增大到一定程度后不再发生变化；第67～70阶的固有频率持续增加，但中间短暂保持不变；第71和72阶的固有频率先基本不变然后不断增大。

双联轴和分扭轴的不同体现在第45～48阶固有频率上，前者始终保持不变，后者在刚度增加时有微小的上升趋势。由图8可知：支撑刚度对高阶频率影响更大，当支撑刚度达到一定数值时，频率随阶数增大依次逐渐增加。

图8 支撑刚度对系统固有频率的影响Fig.8 Influences of support stiffness on the natural frequencies of the system

4.3 模态跃迁现象

当系统刚度改变时，受影响的固有频率曲线逐渐接近，然后在距离很近的位置以较大的曲率迅速分离，这种现象称为模态跃迁。本文以双联轴Ⅰ支撑刚度和扭转刚度、分扭级齿轮副啮合刚度和并车级面齿轮副啮合刚度为例，取第57 阶至72阶固有频率，探究固有频率变化轨迹中的模态跃迁现象。图9 所示为刚度对各阶固有频率的影响。由图9 可见：随着刚度增大，固有频率变化明显，且在遇到相近频率时产生模态跃迁现象。

由图9(a)可见：当双联轴Ⅰ支撑刚度在1×108～1×1010N/m区域内变化时，在A，B，Q，D和E处的2 组固有频率在逐渐靠近后又以不同的曲率分离，均发生了模态跃迁；由图9(b)可见：当双联轴Ⅰ扭转刚度以几何倍数增加时，固有频率逐渐上升，且在F和G处出现模态跃迁；由图9(c)可见：当分扭级齿轮副啮合刚度增加时，系统在H，I和J处产生了模态跃迁现象；由图9(d)可见：受影响的第63和64阶频率以及第71和72阶频率在T处逐渐接近后迅速分开，第61 和62 阶频率和第69 和70 阶频率在L处逐渐接近后迅速分开，均出现模态跃迁。同时，通过对系统刚度变化过程中振动模式的对比分析，发现模态跃迁现象出现时2组固有频率对应的模态振型发生交换，之后维持不变，直至再次遇到频率接近时才发生模态跃迁。

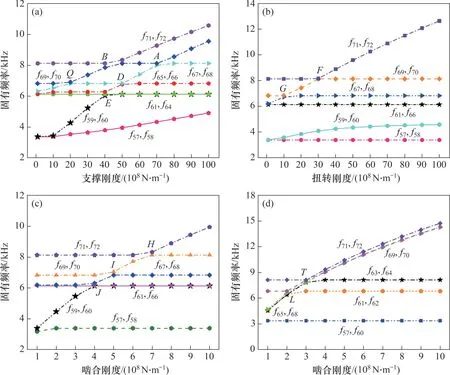
图9 刚度对系统固有频率的影响Fig.9 Influences of stiffness on the natural frequencies of the system

模态跃迁会增加系统动力学行为的复杂性，在系统动态设计中应使刚度尽量避开模态跃迁点，进而避免系统产生多阶次共振现象。

5 结论

1)在7种重根对应的72阶固有频率中，1重根对应的固有频率数最多，且多包含高阶频率；系统包含多个振型，每一传动级齿轮均存在独特的平移振动模式和扭转振动模式，重根数相同的固有频率对应的振型矢量中，多种振动模式并存。

2)在系统正常运行过程中，第12 阶固有频率下的非正交面齿轮支撑弹性变形最大，第46 阶频率下的并车级齿轮副啮合变形最大，第69 阶频率下的输入齿轮平移振动最剧烈，第72 阶频率下的输入齿轮扭转振动最剧烈；对于总的系统模态能，第46 阶频率下的总应变能最大，此时，系统整体变形最大；第60 阶频率下的总动能最大，此时，系统振动最剧烈。

3)系统的固有频率和各齿轮副啮合刚度呈正相关，其中，高阶频率对啮合刚度变化更为敏感，增幅更显著；系统中分扭轴Ⅰ和Ⅱ以及双联轴Ⅰ和Ⅱ对固有频率的影响相似，随着刚度增大，低阶频率基本无变化，中高阶频率随之增加，且当刚度达到一定数值后，频率随阶数增大而逐渐增加。

4)系统刚度的变化会使固有频率在遇到相近频率时产生模态跃迁现象，此时，2组固有频率对应的模态振型发生交换，之后维持不变，直至再次遇到频率接近时才会再次发生模态跃迁；模态跃迁现象的产生意味着系统振动模式的突变，应在动态设计过程中尽可能避免该现象的发生。