面向多核的并发HTM空间池算法

牛德姣，周时颉，蔡 涛，杨 乐，李 雷

(江苏大学 计算机科学与通信工程学院，江苏 镇江 212013)

E-mail：djniu@ujs.edu.cn

1 引 言

层级时序记忆(Hierarchical Temporal Memory，HTM)是一种模拟新大脑皮层结构和功能的机器学习技术[1]，通过对数据空间特征和时序特征的提取及稀疏分布表征(Sparse Distributed Representation，SDR)学习将复杂问题转化为模式匹配与预测，实现数据流的在线分析和预测[2].

与现有人工神经网络模型相比，HTM更接近于人脑认知世界的方式，是受脑启发的新型认知计算模型.传统机器学习算法适合于处理静态数据，以迭代的方式优化给定的训练目标；而HTM依赖于存储的大量模式序列，通过实时感知数据并学习数据的时序依赖进行预测，特别适合于时序、动态数据的在线学习.目前已成功应用于许多数据智能处理领域，如交通流量预测[3]、股票交易数据预测[4]、异常检测[5]等.

HTM模型实现了对脑皮层不同层次功能的模拟，其核心算法包括空间池(Spatial Pooler，SP)算法和时间池(Temporal Memory，TM)算法，其中空间池算法完成输入模式的识别和稀疏离散表征学习，时间池算法完成时序关联模式学习并预测输出[6].通过分析我们发现，在HTM时间池训练中，不仅包含重叠值、近端突触持久值的计算任务，为了学习输入数据的稀疏分布表征，激活与输入模式相匹配的微柱必须搜索整个模型空间，当HTM规模较大或所处理的数据集不断增长时，查找操作将成为影响训练性能的瓶颈.同时，空间池中微柱数量巨大，但是其涉及的计算相对单一且各微柱相互独立，现有的串行计算方式没有针对空间池算法的特点进行优化.当前，多核处理器已经成为主流配置，传统HTM训练方式无法有效利用多核处理器的并行计算能力，导致模型训练时间开销较大.

针对以上问题，本文提出了一种高效的面向多核的并发HTM空间池算法，利用处理器中的多个计算核心优化空间池训练过程.该算法将HTM的微柱区域划分成多个分区，各个分区独立、自主完成分区内微柱选择和近端突触调整，同时利用多核处理器的并发计算能力，并行执行各分区的训练任务，有效利用计算资源，降低空间池训练的时间开销，提高模型的可扩展性和适应能力.

本文的主要贡献点可以总结如下：

1)针对HTM空间池算法训练效率低、无法并行计算，以及其训练过程中存在的大数据问题，提出面向多核的并发HTM空间池算法.利用多核处理器的并行计算能力优化现有HTM空间池的训练，减少模型训练的时间开销，并增强HTM的适应能力.

2)设计基于分区的空间池稀疏表征学习策略，针对空间池算法特点，引入HTM区域分区机制，解决全局搜索活跃微柱速度慢、计算复杂度高的缺点，为空间池算法的并发实现打下基础.

3)引入面向多核处理器的大数据处理方法，利用大量CPU核心的并发计算能力、以及GPU单个核心所不具备的逻辑控制能力，实现并发的活跃微柱选取和突触连接权值调整，提高HTM空间池算法的训练和执行效率.

4)在多核大数据平台Phoenix上，实现了并发HTM空间池算法的原型，并使用NAB、NYC-Taxi和MNIST数据集进行了测试与分析.实验结果表明面向多核的并发HTM空间池算法能大幅减少空间池训练的时间开销，并提高预测准确率.

2 相关工作

首先，我们分析了目前HTM的相关研究工作及神经网络的加速训练技术，并介绍了多核计算平台框架.

2.1 HTM

HTM作为新型的神经形态机器学习算法，模拟了新脑皮质层的组织结构和运作机理，能够以在线方式学习连续的数据流序列.近些年来，研究者针对HTM理论和应用方面展开了深入研究.Yuwei Cui等人[7]将HTM应用于物联网流式数据的学习任务中，满足了实时、连续、在线检测的需要，相较于传统的人工神经网络展现出了更加优异的性能.James Mnatzaganian等人[8]将HTM中空间池的计算过程数学形式化，探索了空间池的学习机制并演示了如何将空间池用于特征学习，所提出的数学形式化框架可用于优化HTM专用硬件的设计.Jeff Hawkins等人[9]的研究表明HTM在噪声环境下执行分类任务时能够保持优秀的鲁棒性，并验证了SDR相较于传统表征方式所具备的优势.Scott Purdy等人[10]使用HTM在流式数据异常检测任务中取得了优异的性能表现，并提出流式数据分析的基本目标是以无监督的方式对每个数据流进行建模，而流式数据本身表现出概念漂移，这需要算法能够实时而不是成批的处理数据.David Rozado等人[11]扩展了传统的HTM模型，添加了一个顶层节点用于存储表示输入模式序列的时空结构实例，这种扩展的HTM模型在一些传统机器学习任务上取得了更好的性能表现.Farzaneh Shoeleh等人[12]提出了使用单编码HTM作为弱分类器的集成学习框架，在不同规模多变量数据库上的实验结果表明单编码HTM在异常检测任务中能取得更好的性能.

以上研究为HTM提供了充分的理论支持，实际应用也展现出其准确性、容错性和鲁棒性等方面优势，但当前研究缺乏针对HTM训练算法的优化，特别是如何利用多核计算架构合理、有效组织HTM训练中的计算任务，进一步提高模型的训练效率和可扩展性还有待深入研究.

2.2 神经网络加速技术

针对神经网络中存在的训练时间开销大的问题，研究人员对模型的加速训练进行了深入研究.目前，神经网络加速训练方法主要包括算法优化、新型架构和专用硬件.

算法优化主要指基于软件的加速训练方法，研究者先后提出了随机梯度下降(SGD)[13]、Momentum[14]、AdaGrad[15]、RMSProp[16]、Adam[17]等参数更新方法，在不改变神经网络模型规模的情况下，依据严格的数学理论，通过优化梯度下降的速度，以更少的时间开销求解损失函数从而达到减少训练时间的目的.另外，模型压缩也是加速神经网络的重要方法，参数修剪和共享[18]、低秩分解[19]、迁移/压缩卷积滤波器[20]和知识精炼[21]等技术已经广泛应用于深度神经网络的压缩与加速.

系统架构方面，利用分布式系统实现异构平台下神经网络的并行式或分布式训练也是提高神经网络训练速度的一种方法.分布式训练分为模型并行[22]和数据并行[23]两种，前者利用分布式系统中的不同机器(Worker Node)分别负责网络不同部分计算，而后者不同的机器保存整个模型的完全拷贝，各计算节点只获得部分数据，参数计算结果通过服务节点(Server Node)整合汇总.Martin Abadi联合谷歌公司提出了TensorFlow[24]，一个灵活的基于数据流的编程模型以及该编程模型的单机和分布式实现.TensorFlow本身提供了并行机制，可以在多种异构系统上执行，最大化地利用硬件资源加速计算.

专用硬件方面，GPU[25]、TPU[26]、FPGA[27]等技术被广泛采用.其中，GPU 和 TPU 针对高度并行化的矩阵运算进行了优化.此外，中国科学院陈天石团队的Diannao家族[28]、普渡大学的Scaledeep[29]、MIT的Eyeirss[30]、HP实验室的基于忆阻器的ISAAC[31]等硬件加速器结构被先后提出.

在HTM加速训练方面，Olga Krestinskaya等人[32]针对HTM计算特点提出了使用数字和混合信号的电路实现，优化了HTM的处理速度和计算资源消耗.Sebastian Billaudell等人[33]在电子微电路中模拟HTM神经元功能结构，将HTM模型移植到集成多个HICANN芯片的海德堡神经形态计算平台上，有助于构建更大规模的HTM并提升计算效率.Abdullah M.Zyarah等人[34]提出了包含空间池和时间池的完整HTM神经形态硬件结构，实验结果表明相比HTM软件实现取得1364倍的加速.

目前，对于HTM的训练优化多集中于利用合适的硬件器件实现加速计算，缺少对于模型结构和计算方式的改进，特别是没有有效利用现有的通用处理器资源.

2.3 多核计算平台

单芯片多处理器(Chip multiprocessors，CMP)，也称多核心，是提高处理器性能的主要技术，现在已成为计算系统的标准配置.然而，利用多个硬件内核进行基于线程的并行编程依然十分困难.Phoenix[35]作为在共享内存的体系结构上的MapReduce实现，可在系统运行时自动管理并行程序的同步、负载平衡和局部性，其目标是在多核平台上，使程序执行得更高效，且使程序员不必关心并发的管理.相较于传统MapReduce框架的分布式实现方式可能会带来额外的通信开销，Phoenix基于多核心和共享内存的特点可以有效避免此问题，因此本文利用Phoenix平台实现了并发HTM空间池训练算法.

3 HTM空间池分析

HTM空间池接收编码器处理后的输入数据并输出SDR作为计算结果，实现输入空间到新特征域的映射，为后续时间池对序列时序关系的学习提供基础，在HTM中发挥着重要作用.空间池算法主要由活跃微柱选取和近端树突调整两个阶段组成，其中活跃微柱选取包括重叠值计算和抑制，是空间池训练中最耗时的部分.

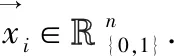
微柱重叠值定义为连接到活跃输入位的连通突触个数.第i个微柱重叠值αi通过如下公式(1)计算：

(1)

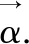
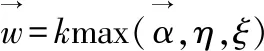
(2)

其中，η表示预设定的微柱稀疏度，kmax方法选取抑制半径ξ内重叠值位于前k大的所有微柱.在空间池学习结束后，这些微柱将被激活，标记为1，未被激活的微柱标记为0，所有微柱的状态构成空间池的SDR输出.

在空间池的学习过程中，依据Hebbian规则调整活跃微柱近端树突上的突触持久值，连通到活跃输入位的突触将增加预设定的持久值，连通到非活跃输入位的突触将减少持久值，以此使输入空间到特征域的映射关系逐渐稳定，实现从输入空间到新特征域的映射，为后续HTM时间池学习输入模式间的时序关系打下基础.

图1给出了HTM空间池的基本结构，图中仅展示了单层的HTM结构.各微柱通过近端树突片段上的突触与输入空间某一局部区域相连接(图中实线与虚线)，连接持久值超过阈值的突触为连接突触(实线)，低于阈值的为潜在突触(虚线).在训练HTM空间池时，微柱是否被激活取决于当前输入下微柱的重叠值及是否受邻近微柱的抑制作用，那些与输入关联越紧密的微柱越有可能被激活.由于抑制作用的存在，在确定激活微柱时需要遍历整个HTM空间池找到重叠值较高的部分微柱，这种线性搜索的时间开销将随着HTM模型规模的增大急剧升高，成为影响空间池训练效率的瓶颈.同时，HTM空间池算法通过抑制机制实现了激活微柱的稀疏分布，并保证所有微柱都有机会参与学习，但在空间池规模较大时，稀疏的活跃微柱仍有可能集中在局部区域，稀疏分布表征强调了微柱分布的稀疏性，但不能保证活跃微柱分布的均匀性.

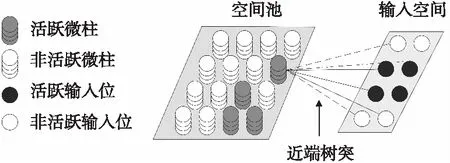
图1 HTM空间池示意图Fig.1 Schematic diagram of HTM spatial pooler

另外，我们发现与深度神经网络普遍采用GPU等硬件进行加速不同，HTM空间池训练中最耗时的并不是重叠值计算等任务，而是为找到活跃微柱需要搜索整个HTM空间，查找、排序操作无法有效借助GPU提高执行效率，并且操作的时间复杂度与模型规模成正比.当前多核处理器已经成为主流，现有HTM空间池算法缺乏相应的优化策略，导致难以发挥多核计算机系统的性能优势提高HTM的训练效率.

为了有效利用多核处理器中大量的计算核心，我们根据HTM空间池算法的特点，引入大数据思维设计了新型的HTM空间池算法.

4 面向多核的并发HTM空间池算法

在第3节分析现有空间池算法局限的基础上，从如何快速选择活跃微柱和高效调整突触持久值两方面改进训练方法，设计面向多核的并发HTM空间池算法.

4.1 基于分区的微柱激活策略

改变当前空间池算法全局选择激活微柱的方式，首先将HTM区域划分为若干个分区，在各分区内独立查找并激活微柱，提出基于分区的微柱激活策略.

如图2所示，将HTM空间池的微柱集合划分为n个分区，在各分区内分别独立控制完成重叠值计算、抑制和微柱激活.对应的过程如算法 1所示：

图2 基于分区的微柱激活策略示意图Fig.2 Schematic diagram of the partition-driven mini-column activation

算法1.The Partition-driven Mini-Column Activation Algorithm

1.partitions=divide(columns，n)

2.forallpartitions∈HTMdo

3.forallcol∈partition.columnsdo

4. col.overlap=0

5.forallsyn∈col.connected_synapses()do

6. col.overlap=col.overlap+syn.active()

7. mo=kmax_overlap(partition.columns，k)

8.forallcol∈partion.columnsdo

9.ifcol.overlap>0andcol.overlap ≥mothen

10. col.active=1

11.else

12. col.active=0

其中，partitions代表所有分区，columns代表HTM所有微柱，divide()方法将所有微柱按照分区数量n分别划分入不同的分区，col代表单个微柱，col.connected_synapses()方法返回所有近端树突上的活跃突触，突触持久值大于阈值则被认为是活跃突触，反之则为非活跃突触，无法参与到重叠值计算过程中.syn.active()方法中，若活跃突触所连接的输入位为“1”，则返回值为“1”，若活跃突触所连接的输入位为“0”，则返回值为“0”.kmax_overlap(C，k)方法返回微柱集合C中重叠值第k大的微柱，mo既是分区中重叠值第k大的微柱，也将作为分区内所有微柱的活跃阈值.参数k指期望的活跃微柱稀疏度，即单个抑制区域内活跃微柱的数量.执行分区操作对应算法 1中第1行，微柱重叠值计算对应2-6行，抑制与激活过程对应7-12行.

与现有HTM空间池全局搜索选择激活微柱的策略不同，基于分区的微柱激活策略将重叠值计算，排序搜索、抑制计算等操作分布在各分区中独立完成.由于分区的规模远小于整个HTM区域规模，排序、搜索的速度大大提高，保证算法时间复杂度有效降低.另外，由于各分区独立选择激活的微柱，能够使学习到的稀疏分布表征在空间池分布得更加均匀，避免了可能出现的局部稠密，有利于提高SDR的表征能力和HTM模型的抗干扰能力；同时各分区的执行流程相对独立，也为利用分布式和并行计算技术提高HTM空间池的训练效率打下基础.

4.2 并发的近端树突调整算法

各分区完成微柱激活后，空间池进一步学习并调整活跃微柱与输入空间相连的近端树突突触持久值.为了提高学习效率，充分发挥计算机系统中多核处理器的计算优势，在基于分区的微柱激活策略基础上，设计并发的近端树突调整算法.

如图3所示，将空间池各分区的训练任务分布到多核处理器中的不同计算核心上，使用多个计算核心并发完成微柱的近端树突调整的任务，执行流程如算法2所示：

图3 并发的近端树突调整Fig.3 Concurrent proximal dendrite adjustment

算法2.The Concurrent Proximal Dendrite Adjustment Algorithm

1.forallpartitions∈HTMdo

2.forallcol∈partition.columnsdo

3.ifcol.activethen

4.forallsyn∈col.synapsesdo

5.ifsyn.active()then

6. syn.p=min(1，syn.p+syn.psyn_inc)

7.else

8. syn.p=max(0，syn.p-syn.psyn_dec)

其中，syn.p指突触syn的持久值，max和min保证持久值位于[0，1]范围内，常量syn.psyn_inc和syn.psyn_dec分别表示突触持久值的增加量和减少量.

并发的近端树突调整算法需要将不同分区的微柱激活和学习任务分布到多核处理器的不同计算核心中，但通常情况下分区数量与计算核心数并不相等，通过以下步骤计算HTM空间池的分区数量.

1)当设定的活跃微柱数量n小于或等于计算核心数m时，HTM将被划分为n个分区，从每个分区中选取1个活跃微柱.

2)当设定的活跃微柱体数量n大于计算核心数m时，取n与m的最大公约数k，将HTM空间池划分为k个分区，每个分区中选取n/k个活跃微柱.

并发的近端树突调整算法能利用现代计算机系统中常见的多核计算核心，由不同核心独立控制对应分区中的计算任务，并发进行突触调整完成学习，减少空间池训练的时间开销；同时，HTM空间池学习算法的并行化有助于提高模型的鲁棒性和可扩展性，使得在有限的训练时间内扩大HTM规模成为可能.

5 原型系统与测试

5.1 原型系统的实现

Phoenix是Stanford大学提出的针对多核计算机的MapReduce平台，可利用多核计算机系统中众多计算核心高效处理数据.我们在Phoenix上实现了面向多核的并发HTM空间池算法，构建了相应的面向多核的并发HTM(Multicore Concurrent Hierarchical Temporal Memory，MCHTM)的原型系统.使用服务器搭建了测试环境，系统配置如表1所示.相同环境下构建了HTM系统，表2给出了HTM和MCHTM的主要参数.由于HTM模型主要用于序列数据的分析与预测，所以我们还使用循环神经网络LSTM模型和HTM、MCHTM进行比较，表3中给出LSTM的主要参数.

表1 原型系统测试环境的软、硬件配置Table 1 Configurations of the prototype test system

表2 HTM原型系统的主要参数值Table 2 Main parameters of the prototype system HTM

表3 LSTM原型系统的主要参数值Table 3 Main parameters of the prototype system LSTM

使用Numenta Anomaly Benchmark(NAB)、New York City Taxi(NYC-Taxi)、 MNIST手写体数字3个数据集，通过序列预测和图像分类两个类型的任务对HTM与MCHTM空间池的时间开销，HTM、MCHTM和LSTM的准确率(Accuracy)和均方根误差(RMSE)等进行测试，每项测试进行10次，取10次测试的平均值作为最终结果.

准确率(Accuracy)通过计算模型产生的预测活跃微柱和下一时刻的实际激活微柱的匹配度得到，两者的重叠率越高说明预测的准确率越高.计算方式如公式(3)所示，C′c表示预测活跃正确的微柱数量，C′p表示预测活跃的微柱数量，Cw表示未被正确预测活跃的微柱数量，Ca表示活跃微柱数量.

(3)

均方根误差(RMSE)计算模型预测值和真实值之间的差异，计算方法如公式(4)所示，T代表序列长度，y′j和yj分别代表预测值和真实值，RMSE值越小表明预测准确度越高.

(4)

5.2 NAB数据集

NAB数据集是美国明尼苏达州交通部采集的车辆通行数据，给出了以10分钟为单位的明尼苏达州双子城都会区每个月所有车辆的平均通行时间，每条数据由时间戳和数值型数据组成，共2500条.

5.2.1 时间开销测试

使用表2中的参数设置，设置活跃微柱数量分别为微柱总数的5%、10%、15%和20%，即20、40、60和80.测试不同迭代次数下HTM与MCHTM空间池的训练时间开销，结果如表4所示.HTM-20、HTM-40、HTM-60和HTM-80分别表示HTM空间池活跃微柱数量为20、40、60和80，MCHTM-20、MCHTM-40、MCHTM-60和MCHTM-80分别表示MCHTM空间池中活跃微柱数量为20、40、60和80.

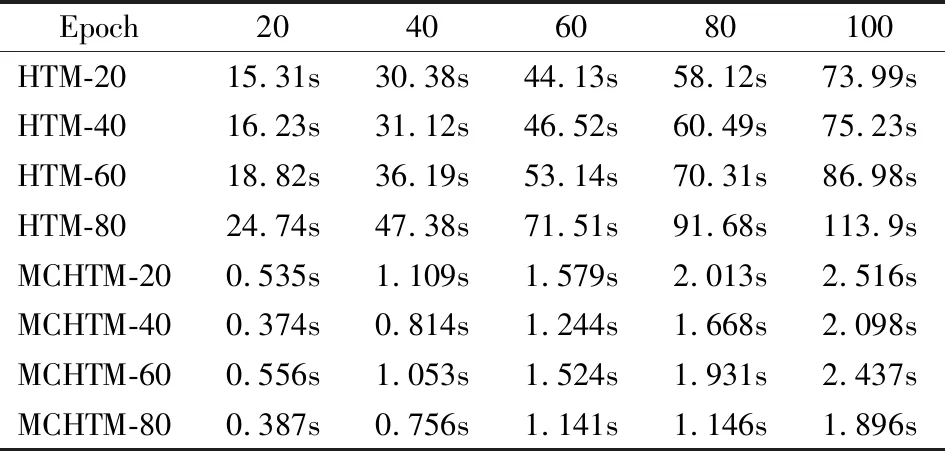
表4 NAB数据集上的训练时间开销测试Table 4 Training time test on NAB dataset

通过表4发现，MCHTM在采用分区结构和并发近端树突调整算法的情况下，相比HTM大幅减少了空间池训练的时间开销.HTM空间池在不同活跃微柱数量下平均训练时间分别为37.72秒、38.57秒、45.25秒和59.21秒，而MCHTM空间池在同等数量活跃微柱下的平均训练时间为1.363秒、1.042秒、1.263秒和1.051秒，训练时间开销显著降低，平均降低了96.39%、97.31%、97.22%和98.23%，表明MCHTM具有明显的效率优势.

同时可以发现，HTM中时间开销与活跃微柱数量呈正比，活跃微柱数量越多，训练时间越长，表明查找活跃微柱是空间池训练时间开销的主要来源，而在MCHTM中，随着活跃微柱数量的增加，训练时间无较大变化.当活跃微柱为40和80时，其时间开销低于微柱数量为20和60时，原因主要在于原型系统测试环境中计算核心数量为40个，当活跃微柱数量设定为20和60时，Phoenix将创建20个并发线程；而活跃微柱数量设定为40和80时，Phoenix将创建40个并发线程.

5.2.2 准确性测试

使用表2中的参数设置，设置活跃微柱数量为微柱总数的5%、10%、15%和20%，即20、40、60和80.测试不同迭代次数和选取不同活跃微柱数量下的HTM和MCHTM在预测任务中的准确率，如图4(a)图所示.选取HTM、MCHTM和LSTM训练时间相近时的RMSE测试结果进行对比，时间开销近似值分别以20、40、60、80、100秒为基准，如图4(b)图所示.

通过图4可以发现，采用了并发空间池算法的MCHTM在极大缩短空间池训练的时间开销的同时，准确率较HTM也有所提升，其原因主要在于采用分区机制后所激活的微柱在HTM区域内分布更加均匀，得到的稀疏分布表征具有更好的表达能力，因此预测准确率有所提高.当活跃微柱数量分别为20、40、60、80时，MCHTM的准确率相比HTM平均上升了4.2%、3.1%、2.7%、2.1%.同时可以注意到每次活跃微柱数量增加所提升的准确率逐渐降低，这主要是因为随着活跃微柱在所有微柱中的占比不断提升，HTM和MCHTM的稀疏均匀水平差距逐渐缩小；MCHTM在激活20个微柱时的准确率仍然高于HTM中激活80个微柱，表明MCHTM利用较少的活跃微柱就可以达到甚至略高于HTM使用较多活跃微柱时的准确率.RMSE值的测试结果与准确率结果类似，MCHTM的RMSE基本低于HTM，当MCHTM激活20个微柱时的RMSE值小于HTM中激活80个微柱的RMSE值，这表明MCHTM在保持与HTM相同准确率的同时，还可以通过减少所需激活的微柱数量进一步减少训练空间池所需的训练时间开销.

图4 NAB数据集上准确率和RMSE测试Fig.4 Accuracy and RMSE test on NAB dataset

随着激活微柱数从20逐步增加到80，每次增加后与前一次相比，HTM的平均准确率分别提高了1.7%、1.1%、0.9%，MCHTM的平均准确率分别提高了0.8%、0.6%、0.3%，HTM的平均RMSE分别下降了1.2%、1.0%、0.5%，MCHTM的平均RMSE分别下降了0.8%、0.6%、0.4%，这表明相较于HTM，MCHTM具有更好的稳定性，改变激活微柱的数量对准确率的影响较小，且在启用较少的活跃微柱时就能达到达到较为理想的准确性.随着活跃微柱数量的增加，MCHTM和HTM准确率的提高幅度以及RMSE的降低幅度都逐渐减少，说明了活跃微柱数量的增加可有效提升HTM的准确性，但提升的幅度有限且会逐渐减少直至收敛.可以认为使用较多或较少的活跃微柱，对于准确率的影响并不明显，在注重准确率的场景下可以启用更多的活跃微柱，而在时间开销敏感的场景下只启用较少的活跃微柱依然可以达到较为理想的准确率.

通过图4中的(b)图还能够看出，在相近的训练时间开销条件下，MCHTM的RMSE均低于HTM和LSTM，这验证了本文所提出的MCHTM算法的有效性，能够在相同的训练时间开销下达到更优的性能表现.此外HTM的RMSE也低于LSTM的，说明了HTM在序列预测任务中相较于LSTM所具有的优势.

5.3 NYC-Taxi数据集

NYC-Taxi是根据纽约市交通管理局实时采集的纽约出租车乘客数量构造的一个数据集，将每隔30分钟的乘客量进行累加，形成共包含10320 条数据的连续数据流.该数据流包含了不同时间尺度下的多种模式，既包括以小时为单位的信息，也包括以天、星期和季度为跨度的信息.相比于NAB数据集，NYC-Taxi数据集的规模更大.以预测未来5个时间步(2.5小时)出租车乘客数量为任务测试模型性能.

5.3.1 时间开销测试

使用表2中的参数设置，设置活跃微柱数量为微柱总数的5%、10%、15%和20%，即20、40、60和80.测试不同迭代次数下HTM与MCHTM空间池的时间开销，结果如表5所示.

表5 NYC-Taxi数据集上的训练时间开销测试Table 5 Training time test on NYC-Taxi dataset

由表5可知，HTM空间池在不同活跃微柱数量下平均训练时间为173.36秒、176.84秒、207.99秒和231.46秒，而MCHTM空间池在同等数量活跃微柱数量下平均训练时间为6.18秒、4.76秒、5.82秒和4.54秒，相较于HTM空间池，MCHTM空间池训练时间开销平均降低了96.44%、97.31%、97.21%和98.04%.NYC-Taxi数据集的规模约为NAB数据集的4倍，但实验结果表明MCHTM仍然保持了较高的训练时间开销降低比率，与NAB数据集中的测试结果基本一致.

5.3.2 准确性测试

使用表2中的参数设置，设置活跃微柱数量为微柱总数的5%、10%、15%和20%，即20、40、60和80.测试不同迭代次数和选取不同活跃微柱数量下HTM和MCHTM在预测任务中的准确性，取5个时间步预测结果平均值，如图5(a)图所示.选取HTM、MCHTM和LSTM训练时间相近时的RMSE进行对比，训练时间开销近似值分别以100、200、300、400、500秒为基准，如图5(b)图所示.

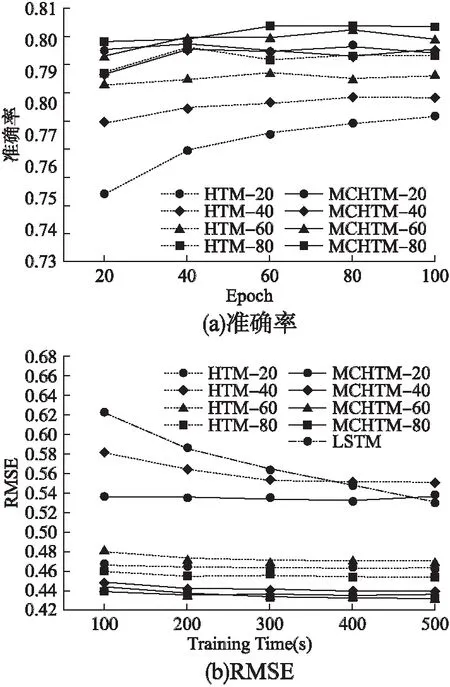
图5 NYC-Taxi数据集上准确率和RMSE测试Fig.5 Accuracy and RMSE test on NYC-Taxi dataset

通过图5可以发现，当活跃微柱数量分别取20、40、60、80时，相较于HTM，MCHTM的平均准确率分别提高了3.6%，1.6%，1.4%，0.7%，RMSE平均分别下降了3.9%，1.5%，0.9%，0.4%，准确性的提升效果略低于NAB数据集，MCHTM在较大数据集上的准确率提升表现没有小数据集上的优异，但准确率依然高于HTM.MCHTM在激活20个活跃微柱时的准确率和RMSE均与HTM激活80个微柱时相当，表示MCHTM具有更好的可扩展性.

NYC-Taxi数据集的实验结果表明，相较于较小规模的NAB数据集，MCHTM在较大数据集场景下准确率的提升幅度虽然略有降低，但整体上依然具有较高的准确率，特别是能够大幅提高空间池的训练效率，在使用较少活跃微柱的情况下即可达到和HTM激活较多微柱时相当的性能.

除HTM和MCHTM的对比分析所能得到以上结论外，通过图5中的(b)图的实验结果还可以看出，在NYC-Taxi数据集上可得到的结论和NAB数据集所得结论基本一致，验证了本文所提出的MCHTM算法相较于HTM以及LSTM的优势.

5.4 MNIST数据集

MNIST数据集由60000个训练样本和10000个测试样本组成，每个样本都是一张28×28像素的灰度手写数字图片.从60000个训练样本中随机抽取数字图片0-9分别各100个，共1000个数字图片作为训练集，以原有的10000个测试样本作为测试集.

5.4.1 时间开销测试

设置活跃微柱数量为微柱总数的5%、10%、15%和20%，即20、40、60和80.测试不同迭代次数下HTM与MCHTM的空间池的训练时间开销，结果如表6所示.

通过表6发现，基于MNIST数据集的时间开销测试中HTM空间池在不同活跃微柱数量下平均训练时间为183.8秒、197.8秒、215.1秒和233.7秒，而MCHTM空间池在同等数量活跃微柱数量下平均训练时间为8.99秒、5.41秒、9.98秒和6.03秒，相较于HTM空间池，MCHTM空间池训练时间开销平均降低了95.11%、97.27%、95.37%和97.42%.基于MNIST数据集上的实验结果表明MCHTM仍然保持了较高的空间池训练时间开销降低比率，与NAB和NYC-Taxi数据集中的测试结果基本一致.

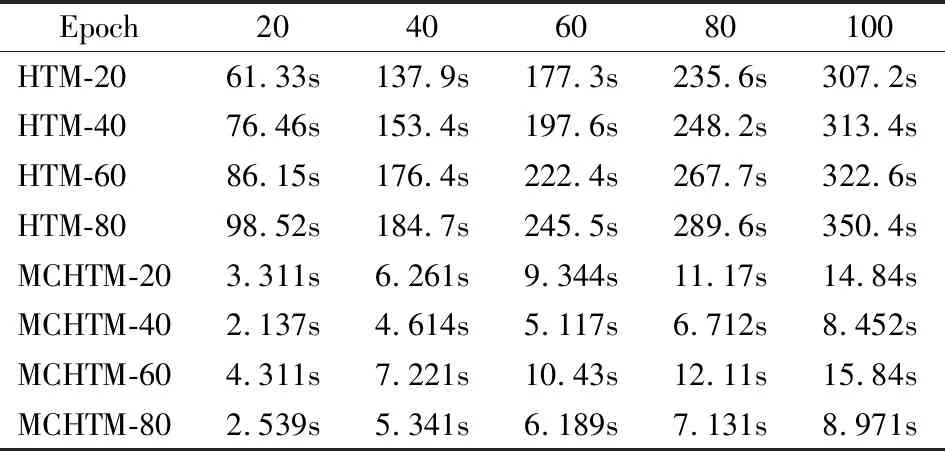
表6 MNIST数据集上的训练时间开销测试Table 6 Training time test on MNIST dataset

5.4.2 准确率测试

设置活跃微柱数量为20、40、60和80，测试HTM、MCHTM和LSTM训练时间相近时的准确率进行对比，时间开销近似值分别以100、200、300、400、500秒为基准，如图6所示.

图6 MNIST数据集上的准确率测试Fig.6 Accuracy test on MNIST dataset

通过图6可以发现，当活跃微柱数量分别取20、40、60、80时，相较于HTM，MCHTM的平均准确率分别降低了0.61%、0.94%、0.45%、0.54%.在相同的迭代次数下，MCHTM在图像分类任务中的准确率相较HTM有所降低.但在相同训练时间的条件下，由于MCHTM能够完成更多次的训练迭代，从而使得MCHTM的准确率优于HTM.同时还发现时间开销相同的条件下，HTM在图像分类任务中，其准确率低于LSTM，而MCHTM利用自身多核并发的计算特点，在相同时间内完成了更多次的训练迭代，从而达到了优于HTM和LSTM的准确率性能表现，从而验证了本文所提出的MCHTM所具备的效率和性能优势.

6 总结与展望

针对现有HTM空间池训练算法时间复杂度高的问题，提出了一种高效的面向多核的并发HTM空间池算法，包含基于分区的微柱激活策略和并发的近端树突调整算法.通过将HTM区域进行分区，在各分区内独立完成训练任务，从而降低搜索活跃微柱巨大的时间开销，同时分区策略还能够有效利用CPU中大量的计算核心，使空间池的训练能够在多个核心上并行完成.利用Phoenix多核计算平台实现了算法原型，在NAB、NYC-Taxi和MNIST这3个数据集上针对训练时间开销、准确率(Accuracy)和均方根误差(RMSE)进行了测试与分析，实验结果表明在多核平台上基于分区的并发HTM空间池算法能够降低96.39%～98.32%的训练时间开销，同时模型准确率平均提升了0.7%～4.2%，验证了所提出算法的有效性.

本文的研究重点在于改进现有HTM空间池的基本结构和计算方式以提升训练效率，在接下来的研究工作中，我们将进一步思考如何将并发思想应用到更复杂的HTM时间池计算中，提高整个HTM模型的训练效率.