求解时变凸二次规划的变参积分动态学习网络

陆荣秀，黄 伟，杨 辉，张智军

1(华东交通大学 电气与自动化工程学院， 南昌 330013)

2(江西省先进控制与优化重点实验室， 南昌 330013)

3(华南理工大学 自动化科学与工程学院，广州 510640)

E-mail：1583395293@qq.com

1 引 言

时变二次规划(quadratic programming，QP)问题在诸多领域，如约束最小二乘问题求解[1]、非线性优化问题[2]、经济数学[3]、系统分析[4]等中都发挥着至关重要的作用.一般而言，QP问题的求解方法都是基于迭代计算思想求解，如拉格朗日法[5]、Lemke算法[6]、内点法[7]等.然而，这些方法即使依靠高性能计算机，求解依然需要较长时间，特别是在求解大规模的实时问题时表现较差.因此，寻找更加高效的求解方法始终是研究人员的目标.

近年来，人工神经网络因其自我学习，快速寻优的特点被广泛应用于求解最优化问题.基于人工神经网络的特点，研究者希望利用神经网络加速QP问题求解过程以缩短求解时间.基于梯度下降理论，文献[8]提出了梯度神经网络 (gradient-based neural network，GNN)，该网络主要用于求解静态凸QP问题[9].然而面对时变QP问题时，GNN无法实时追踪理论解而无法收敛.针对这个问题，张雨浓[10]等人提出了零化神经网络(zeroing neural network，ZNN).该网络能实时追踪时变QP问题并保持收敛，极大地提高了计算效率，被广泛应用于求解时变问题，如求解时变Sylvester方程[11]，时变动态矩阵反演[12]，时变二次规划问题[13]等.然而，ZNN虽然弥补了GNN无法实时追踪时变问题理论解的缺点，但也有收敛时间过长的不足之处.为了克服ZNN的这一缺点，文献[14]提出了一种变参收敛微分神经网络(varying-parameter convergent differential neural network，VP-CDNN) 以加快计算速度，缩短收敛时间.VP-CDNN比ZNN有更快的指数级收敛速率，被应用于解决许多最优控制问题，如冗余关节角漂移[15]，时变Sylvester方程[16]等.然而，囿于硬件而参数较差时，VP-CDNN表现也并不理想，所以寻找更快更好的神经网络依然是研究者的目标.

因此，本文提出了一种新型变参积分动态学习网络(varying-parameter integral dynamic learning network，VP-IDLN).与传统的微分神经网络不同，VP-IDLN采用误差积分法设计，控制策略灵活，具有超指数级收敛速率，收敛性质和鲁棒性良好.实验证明VP-IDLN在参数设置较差时，也有较好收敛速率，下限较高.与GNN、ZNN和VP-CDNN相比，收敛时间是其几十分之一，收敛速率提升显著.

2 时变凸QP问题的数学形式

受线性约束时变凸QP问题的数学形式为：

minimize：xT(t)J(t)x(t)/2+kT(t)x(t)
subject to：D(t)x(t)=l(t)

(1)

为求解式(1)中x(t)，定义拉格朗日函数：

L(x(t)，λ(t)，t)：=xT(t)J(t)x(t)/2+kT(t)x(t)
+λT(t)D(t)x(t)-λT(t)l(t)，t∈[0，+∞)

(2)

式中λ(t)∈Rm表示拉格朗日乘子，x(t)是未知变量.由拉格朗日乘数法[17]可知，当L(x(t)，λ(t)，t)的偏导数连续且存在时，凸QP问题(1)有最优解.则方程(2)满足以下条件：

(3)

为使式(3)更为简洁，可写为分块矩阵形式：

P(t)y(t)=q(t)

(4)

式中P(t)是一个可逆的方阵以保证式(4)有且仅有唯一解.

为逼近时变QP问题的最优解，定义以下误差函数：

H(t)：=P(t)y(t)-q(t)

(5)

当H(t)收敛至零时，方程(5)等价于方程(4).

3 变参积分动态学习网络

3.1 变参积分动态学习网络设计

基于神经动力学设计经验[18]，提出一种新型误差积分公式：

(6)

式中H0=H(0)=P(0)y(0)-q(0)代表方程(6)在t=0时的初始值.其中P(0)，q(0)，y(0)分别是P(t)，q(t)，y(t)的初值.由神经网络理论[19]，于式(6)中引入相关系数和激活函数，获得新的误差积分神经动力学公式：

(7)

式中α，β>0是用来控制收敛速率的固定值标量参数，exp(-(t+5))是时间t有关的指数型时变量.此外，Φ(·)：Rm×n→Rm×n代表了单调递增的奇函数.值得一提的是ω是方程(7)的初值且ω=βΦ(H(0)).

把方程(5)代入方程(7)可得：

(8)

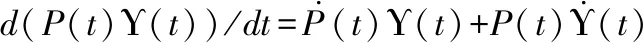
(9)

将方程(9)代入方程(8)，可得变参积分动态学习网络(VP-IDLN) 的数学模型：

(10)

根据VP-IDLN的数学模型，绘出相应的系统流程图如图1所示.

图1 VP-IDLN数学模型的系统流程图Fig.1 System flow chart of VP-IDLN mathematical model

3.2 VP-IDLN的收敛性分析

在本节进一步探讨分析VP-IDLN的收敛性质.

定理1.已知时变系数矩阵J(t)，k(t)，D(t)，l(t)，使用VP-IDLN求解时变凸QP问题且其激活函数为单调递增奇函数Φ(·)时，状态变量y(t)总是可以收敛至理论解y*(t).

(11)

(12)

其次，为方便推导，写出方程(7)的标量形式：

(13)

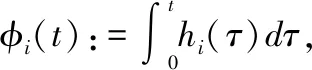
(14)

由李雅普诺夫理论[22]，构建一个新的李雅普诺夫函数为：

vi(t)=(ωi-αφi(t))2/2

(15)

对vi(t)求导有：

(16)

考虑到φi(t)的定义并结合方程(14)，可得：

=-αβe-(t+5)hi(t)φ(hi(t))

(17)

证明成立.

本文使用的激活函数如图2所示，分别是linear，power和leaky relu函数.

图2 求解时变QP问题VP-IDLN所用激活函数Fig.2 Activation function for solving the time-varying QP problem with VP-IDLN

Linear：φ(x)=x式中x代表了标量或矩阵且定义不变；

Power：φ(x)=xu，u≥3且是奇数；

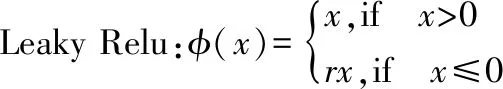
事实上，leaky relu函数是一种特殊的单调递增奇函数，除了不满足-f(x)=f(-x)在数值上的要求，具有其他奇函数的一切性质.

定理2.已知时变凸QP问题的系数矩阵J(t)，k(t)，D(t)，l(t)，VP-IDLN的状态变量y(t)在使用linear激活函数时可以收敛至唯一理论解y*(t)，收敛速度能达到超指数级，其具体收敛速率为(αet+5-5β-βt)/βt.

证明：当选择linear函数φ(x)=x，x∈R为激活函数，方程(7)变为：

(18)

方程(18)是一个典型的一阶线性微分方程，其通解为：

(19)

对φi(t)求导，得hi(t)为：

(20)

(21)

综上所述，VP-IDLN使用linear激活函数时有超指数级的收敛性质，其收敛速率为(αet+5-5β-βt)/βt.

证明成立.

定理3.已知时变系数矩阵J(t)，k(t)，D(t)，l(t)，使用power函数作为激活函数求解时变凸QP问题时，VP-IDLN的状态变量y(t)可以收敛至唯一理论解y*(t).其具体的收敛性质如下所示：

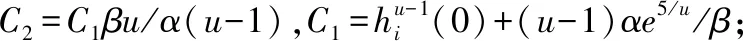
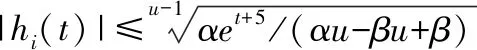
(22)

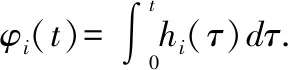
(23)

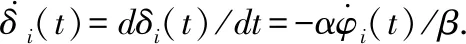
(24)

将式(24)改写成可分离变量形式，有：

(25)

对式(25)两边同时积分，得到一个关于时间t的方程：

(26)

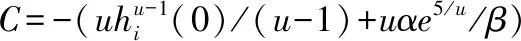
(27)

由δi(t)的定义可得φi(t)为：

(28)

(29)

因为u>1所以有(u-1)e(t+5)/u/u2>0.根号内-α(u-1)e(t+5)/u/βu+C1是一个单调递减函数.当α(u-1)e(t+5)/u/βu=C1时其收敛时间为Tcon=ulnC2-5，其中C2=C1βu/α(u-1).由单调递减函数的性质可知，当t∈[0，Tcon]时，函数-α(u-1)e(t+5)/u/βu+C1≥0.当t∈(Tcon，+∞)时，hi(t)<0，方程(29)在实数域内无解.这是因为u是大于1的奇数，所以u-1必为偶数，而偶数方根内数必须为非负数，其互相矛盾而无解.

综上所述，hi(t)在t≥Tcon时可收敛至零.

(30)

总而言之，VP-IDLN的收敛性质可以表述为：

至此，证明了VP-IDLN可以在有限时间内收敛，接下来讨论其收敛速率.

由方程(30)不能直接获得hi(t)收敛速率，因而通过与linear激活函数比较来判定其收敛速率.

由式(22)可知，VP-IDLN使用power函数时hPi(t)为：

(31)

式中hPi(t)的下标P代表power函数.然后对hPi(t)求导得其导数为：

(32)

类似的，通过对方程(18)求导能够得到VP-IDLN使用linear激活函数时hLi(t)导数为：

(33)

式中L是hLi(t)的下标，代表使用了linear函数时hi(t)的值.为了方便比较linear函数和power函数的收敛速率，假定存在某时刻满足hPi(t)=hLi(t)=hi(t)，然后有以下不等式：

(34)

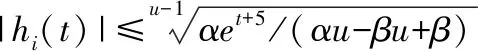
证明成立.

定理4.已知时变凸QP问题的系数矩阵J(t)，k(t)，D(t)，l(t)，当使用leaky relu激活函数时，VP-IDLN能够以超指数级的收敛速率完成收敛.当hi(t)>0时，收敛速率为(αet+5-5β-βt)/βt.当hi(t)≤0时，收敛速率为(αet+5-r5β-rβt)/rβt.式中r是一个很小的正数.

证明：leaky relu函数本质上与linear函数差别不大，仅在hi(t)≤0时多了一个系数r，为节省空间，证明过程可参见定理2，在此不再赘述.

3.3 VP-IDLN的鲁棒性分析

当模型出现扰动误差时，VP-IDLN的数学模型可写为：

(35)

式中ΔO(t)∈Rm×n代表的是模型中扰动误差.

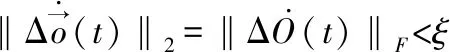
证明：为便于推导，将方程(35)改写为如下矢量形式：

(36)

(37)

类似于收敛性证明，根据李雅普诺夫稳定性定理，先定义一个适当的李雅普诺夫函数.则先定义函数：

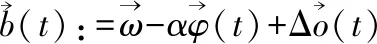
(38)

(39)

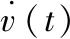
(40)

(41)

结合公式(41)与李雅普诺夫稳定性理论，对以上两种情况进行细致分析.特别地，|hi(t)|是非负数且φ(·)是单调递增的奇函数.所以αφ(|hi(t)|)是一个非负数.

(42)

将不等式(42)代入方程(12)，得到状态解y(t)和理论解y*(t)间的误差‖(t)‖2为：

(43)

综上所述，即使VP-IDLN中存在干扰误差，VP-IDLN也具有良好的鲁棒性，能排除干扰，快速收敛到一个稳定值.

证明完毕.

4 实验与分析

本节首先通过仿真实验验证不同参数α，β对VP-IDLN收敛速率的影响.其次进一步分析参数改变对VP-IDLN鲁棒性的影响.最后，在使用linear，power与leaky relu激活函数的情况下，将VP-IDLN与传统的微分神经网络(即GNN，ZNN，VP-CDNN)进行比较，证明VP-IDLN具有更好的收敛性能和更短的收敛时间.

4.1 时变凸QP问题的系数矩阵

在进行仿真实验前，不失一般性，参数矩阵J(t)，k(t)，D(t)，l(t)分别设为：

(44)

式中Ci=cos(i*t)且Si=sin(i*t).此外，时变凸QP问题理论解y*(t)和状态解y(t)可以写成：

(45)

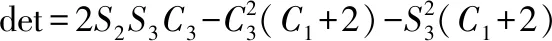
式中ya，yb，yc都是随机数.

4.2 参数选择

本部分将探究不同参数值α和β对VP-IDLN收敛性质的影响，详实的实验结果数据如表1、图3和图4所示.不失一般性，本部分实验选用linear函数为激活函数，使用控制变量法，固定一个参数，不断改变另一个参数，进行六次独立重复实验.

表1 使用linear激活函数，VP-IDLN不同参数对应收敛时间Table 1 Convergence time of VP-IDLN with linear-type activation function and different parameters α and β

首先，由图3(a)可知，当α=1，β=0.01时，状态变量y(t)收敛至唯一理论解y*(t)的时间为0.0028s.当α=1，β=0.1时，从图3(b)可知，误差‖(t)‖2的收敛时间为0.0057s.当α=1，β=1，根据图3(c)，状态分量y1(t)，y2(t)收敛至理论解分量和时间是0.032s.其次，由图4(a)，当α=0.1，β=0.1时，状态变量y(t)在0.031s内收敛至理论解y*(t).当α=1，β=0.1时，如图4(b)所示，状态分量y1(t)和y2(t)能在0.0057s内从随机初值收敛至理论解分量与当α=10，β=0.1时，根据图4(c)，误差‖(t)‖2完成收敛过程需要0.0025s.因此，可知VP-IDLN的收敛速度受参数α，β影响，保持参数α不变，增大β，VP-IDLN收敛时间也随之变大；保持参数β不变增大α，VP-IDLN的收敛时间缩短.

最后，基于图3和图4的数据和实验，作出了关于VP-IDLN不同参数所对应的收敛时间表1.由表1可知，当参数α=1时，增大β而减少参数比值α/β(具体值为100，20，10，2，1)，VP-IDLN的收敛时间会逐渐增大 (为0.0028s，0.0031s，0.0057s，0.018s，0.032s).保持β=0.1，增加α的值而增大比值α/β(具体值为1，5，10，50，100)，VP-IDLN的收敛时间逐渐变小 (分别为0.031s，0.006s，0.0057s，0.0047s，0.0025s).

图3 保持α不变，增大β时VP-IDLN的计算误差‖(t)‖2Fig.3 Computational error‖(t)‖2of the VP-IDLN when parameter α remains unchanged and β becomes larger

图4 保持β不变，增大α时VP-IDLN的计算误差‖(t)‖2Fig.4 Computational error‖(t)‖2of the VP-IDLN when parameter β remains unchanged and α becomes larger

综上所述，VP-IDLN的收敛时间与参数α和β的比值密切相关，α/β的值越大，其收敛时间越短，收敛速度越快.值得一提的是，即使在参数设置较差的情况下，VP-IDLN最长的收敛时间依然小于0.04s，比传统微分神经网络在参数较好下的收敛时间还要短(参见4.4节图7(a)中linear激活函数GNN，ZNN和VP-CDNN的收敛时间).可见，VP-IDLN在参数设置不佳时也有很快的收敛速率，拥有较高的下限.

4.3 鲁棒性分析

与收敛性实验类似，在使用linear激活函数的前提下，使用控制变量法，固定一个参数，改变另一参数，进行6次独立重复实验.本次实验中，干扰误差为：

ΔO(t)=[0.02cost，0.03sin2t，0.02sin4t]T

其实验结果如图5、图6和表2所示.综合图5和图6可知，模型中存在误差VP-IDLN也能较好的消除其影响，快速收敛并趋于稳定，收敛曲线几乎没有振荡.其收敛性质与4.2节分析一致.但其缺点也较明显，参数选择较差时VP-IDLN的误差无法完成收敛，会趋于一个较为稳定的值.事实上，这个稳定值也不可能是一条直线，仔细观察，其有极小幅度的波动.选择该曲线最大波动值称为最大误差来衡量其波动幅度.由图5可知，保持α不变，增大β，VP-IDLN 的误差‖(t)‖2的最大误差变化极小.从图5(a)-图5(c) 可知，β的增大对VP-IDLN最大误差影响微乎其微，其最大误差近似相等，其值在0.157 左右浮动，更多详细数据可见表2.

图5 保持α不变，增大β且模型中存在扰动误差时VP-IDLN的计算误差‖(t)‖2=‖y(t)-y*(t)‖2Fig.5 Computational error‖(t)‖2of the VP-IDLN when parameter α remains unchanged and β becomes larger with disturbance

图6 保持β不变，增大α且模型中存在扰动误差时VP-IDLN的计算误差‖(t)‖2=‖y(t)-y*(t)‖2Fig.6 Computational error‖(t)‖2of the VP-IDLN when parameter β remains unchanged and α becomes larger with disturbance

表2 使用linear激活函数，VP-IDLN不同参数对应最大误差Table 2 Maximum error of VP-IDLN with linear-type activation function and different parameters α and β

与之相对，保持β不变，增大α，VP-IDLN的最大误差有显著变化.当α=1，β=1时，由图6(a)可知，VP-IDLN的最大误差是0.165.当α=5，β=1时，根据图6(b)，最大误差降至0.031.当α=10，β=1时，从图6(c)可得，VP-IDLN的最大误差已经满足收敛要求，为0.015. 综上所述，保持β不变，增大α，VP-IDLN 的最大误差会不断下降，直至满足收敛要求.

除此之外，根据图5和图6与实验数据，制作了数据详实的表2.显而易见，在模型中存在干扰误差的情况下，参数α，β对其鲁棒性的影响各不相同，当α=1，β=0.01，0.05，0.1，0.5，1时，VP-IDLN的最大误差分别为0.154，0.156，0.157，0.159，0.161.当β=1，α=1，2，5，8，10时，VP-IDLN 的最大误差为0.167，0.076，0.033，0.018，0.015.综上所述，两个参数中α对VP-IDLN 的鲁棒性影响较大，α的值越大，其鲁棒性也就越好，收敛速度越快，抗干扰能力越强.现实生活中，可以根据需要，选择合适的参数.

4.4 与传统微分神经网络比较

本小节，在使用linear，power和leaky relu函数的情况下，将VP-IDLN与传统的微分神经网络进行比较，以验证VP-IDLN具有更好的收敛性质与更快的收敛速率.在本次实验中，3种神经网络都选用了一样的系数矩阵和相应的激活函数.此外，还保证了微分神经网络GNN，ZNN和VP-CDNN的参数γ=10等于VP-IDLN的α/β.特别地，leaky relu函数中r=0.1.其实验结果见图7.

由图7(a)-图7(c)可知，无论使用何种激活函数，VP-IDLN的收敛速率总是最快，其收敛时间是GNN，ZNN，VP-CDNN的十分之一，甚至更快.如图7(a)所示，当激活函数为linear函数时，VP-IDLN，ZNN，VP-CDNN都能在有限时间内完成收敛，而GNN保持大幅度的震荡无法收敛.然而，VP-IDLN能够在0.005s内完成收敛，而VP-CDNN与ZNN需要0.55s，差距较为明显.当power函数作为激活函数时，从图7(b)可知，VP-IDLN依然有最快的收敛速率，在0.005s内完成了收敛.与之相对的是GNN，ZNN与VP-CDNN都无法在2s内完成收敛.GNN因其不能实时追踪时变解依然保持大幅度的震荡，而ZNN与VP-CDNN虽然有下降的趋势，但收敛速度过慢而无法在2s内结束收敛.在使用leaky relu函数时，其差别也更大.VP-IDLN依然可以在0.005s内完成收敛，但其他神经网络都无法在2s内完成收敛，尽管把时间尺度放大到10s，VP-CDNN依然需要3.9s才能完成收敛.ZNN虽然有收敛的趋势，但无法在有限时间内完成收敛.GNN一如既往保持振荡，无法实时追踪理论解，效果较差.

图7 在使用不同激活函数求解时变凸QP问题时，VP-IDLN的误差‖(t)‖2与传统微分神经网络GNN，ZNN和VP-CDNN的比较Fig.7 Online solutions to convex QP problem and the computational error‖(t)‖2=‖y(t)-y*(t)‖2 of VP-IDLN with different activation functions compared with GNN，ZNN，VP-CDNN

综上所述，在保持参数一致的情况下，无论选用何种激活函数，拥有超指数级收敛速率的VP-IDLN的收敛性能总是好于传统的微分神经网络GNN，ZNN和VP-CDNN.

5 结束语

为了求解受约束的时变凸QP问题，本文提出了一种新型的变参积分动态学习网络 (VP-IDLN).首先，该神经网络设计参数为指数型，具有时变、灵活和自适应调整的特点.其次，通过理论分析，证明了VP-IDLN具有全局收敛性，在选用不同激活函数时拥有超指数级的收敛速率，实现了超指数率收敛.然后，分析证明了VP-IDLN具有良好的鲁棒性，抗干扰能力较强.最后，通过仿真实验证明了VP-IDLN具有良好的收敛性能，即使在参数不佳的情况下也有良好的表现，下限较高.除此之外，相同参数设置下VP-IDLN的收敛速率也远快于传统微分神经网络GNN，ZNN 与VP-CDNN.