非互易Aubry-André 模型的经典电路模拟*
2022-08-28成恩宏郎利君2
成恩宏 郎利君2)†
1)(华南师范大学物理与电信工程学院,广东省量子调控工程与材料重点实验室,广州 510006)
2)(华南师范大学量子物质研究院,广东省核物质科学与技术重点实验室,广州 510006)
非厄米的引入扩展了传统厄米量子系统中的概念并诱导出许多新奇的物理现象,比如非厄米系统所独有的非厄米趋肤效应,这使得对非厄米量子模型的模拟成为大家关注的热点.相比于量子平台,经典系统具有成本低廉、技术成熟、室温条件等优势,而其中的经典电路系统则更加灵活,原则上可以模拟任意维度、任意格点间跃迁、任意边界条件下的量子紧束缚模型,已经成为模拟量子物态的有力平台.本文利用经典电路通过SPICE 成功模拟了一个重要的非厄米量子模型——非互易Aubry-André 模型——的稳态性质,此模型同时具有非互易的格点跃迁和准周期的格点在位势.以此为例,详细介绍了如何建立经典电路的拉普拉辛形式与量子紧束缚模型哈密顿矩阵在不同边界条件下的映射,尤其是如何利用电流型负阻抗变换器构建模型的非互易性.然后,根据电路的格林函数,通过AC 电流驱动并测量电压响应的方式,用SPICE 模拟了周期边界条件下的复能谱和相应的能谱缠绕数,以及开边界条件下的趋肤与局域模式的竞争.其中,为了使电路的响应不发散,本文还解析地给出辅助元件的设置原则.结果显示,SPICE 模拟与理论计算很好地符合,为进一步的实验实现提供了详细的指导.由于本文电路设计与测量方案的普适性,原则上可以直接应用于其他非厄米量子模型的电路模拟.
1 引言
近些年,非厄米物理[1]引起了物理学各个领域的广泛关注,它除了传统上可以描述经典系统中增益损耗带来的现象,还被用来描述量子开放系统的性质[2].不同于封闭系统的厄米哈密顿量,非厄米的引入扩展了传统量子力学的范式[3],如复数能谱、双正交基等,这诱导出许多新奇现象: 手征-时间反演对称性(PT 对称性)的破缺[4-9]、非厄米简并点[10,11]、模式转换(mode switching)[12]等.非厄米性同样扩展了大家对拓扑态的理解.一个典型的反常是,在厄米拓扑系统中作为基本原则的体-边对应关系在非厄米系统中不总是适用[13-26],而仅在非厄米系统中存在的非厄米趋肤效应[16,23]被认为是此原则失效的一个重要原因.非厄米趋肤效应的发现引发了对传统的厄米量子效应与其竞争关系的广泛研究,如与安德森局域化的竞争[27-33]和与Hubbard相互作用的竞争[34-39]等.
鉴于非厄米物理的重要性,在实验上模拟非厄米模型及其独有的新奇现象就显得格外重要.相比传统的量子平台(如冷原子系统[8,9,40]),经典系统对于模拟非厄米模型有着天然的优势,除了成本低廉、技术成熟等特点,它可以非常直接地利用自身的增益和损耗实现非厄米性,并已成为模拟非厄米系统的有力平台,如光学系统[7,41-45]和机械系统[46,47]等.其中,经典电路系统因其不受限的网络形式和高度的调控自由度,原则上可以模拟任意维度、任意格点间跃迁、任意边界条件下的量子紧束缚模型,成为量子系统模拟的有力竞争者.目前在电路系统下已经成功实现了很多非厄米的量子模型及其现象,如PT 对称性破缺[48,49]、非互易Su-Schrieffer-Heeger (SSH)模型[50,51]、二维非互易陈绝缘体[52,53]、非互易高维模型[54,55]、非互易狄拉克模型[56]及非厄米异常线[57]等.
对于非厄米趋肤效应与准无序的竞争关系,文献[27]提出了非互易(non-reciprocal)Aubry-André(AA)模型:
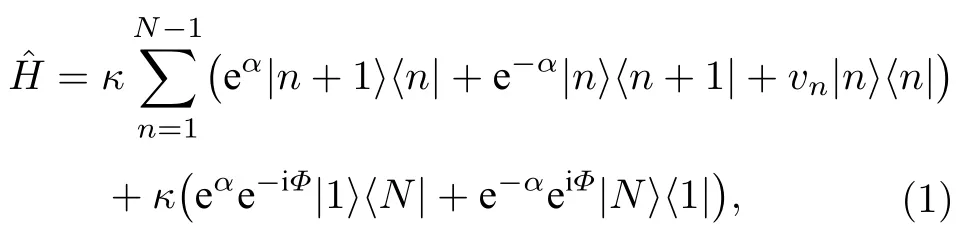
其中,κe±α描述最近邻格点间的跃迁强度,如0表示前后两方向的跃迁强度不相等,即跃迁具有非互易性;vn2λcos(2πβn)表示在位的准周期/无序势,λ表示无序强度,β一般取无理数.对于有限尺寸的系统,可以取格点数NFs且βFs-1/Fs以保证准周期势的周期与格点的周期在系统尺寸内不匹配,其中Fs表示斐波那契数列的第s个值.为清楚表示有限尺寸下的边界条件,在(1)式中特别将首尾之间的跃迁项显示写出(第二个圆括号内),并且可以表示在整个一维环中间加入磁通Φ后的哈密顿量(取特定规范后).为方便后面的电路模拟,以格点态{|n〉}为基矢写出哈密顿量的矩阵形式:

此模型的非厄米拓扑性质以及趋肤效应与局域化的竞争关系,文献[27]已经在理论上详细讨论,这里简单回顾下主要结论: 在周期边界条件下,准无序强度较弱(λ<max{eα,e-α}≡λc)时,系统的本征态为扩展态,其本征能谱在复平面上为绕原点的圈,表明处于非厄米拓扑相,可由能量缠绕数ν±1 表征;随着准无序强度的增强,当λ>λc时,系统的本征态经历从扩展态到局域态的转变,与此同时,本征能谱收缩成实轴上的一条线,表明处于拓扑平庸相,相应的能量缠绕数ν0 .有趣的是,拓扑相变与局域相变点完全一致,这是由于局域化改变了系统的本征能谱在复平面的分布,进而影响了能量缠绕数.相应地,在开边界条件下,因为局域的转变使系统对边界不再敏感,系统具有同样的相变点,区别只是拓扑相区的本征态由于趋肤效应变为趋向某一边缘(由α的正负决定哪个边缘),且本征能谱变为实数;局域相区的本征态两边的衰减长度变得不同.
本文的主要目的是通过对非互易AA 量子模型的经典电路模拟,详细介绍如何用电路的拉普拉辛形式模拟量子紧束缚模型,便于感兴趣的读者利用类似方法模拟其他量子模型,以及为实验实现提供详细指引.剩下的内容安排如下: 第2 节详细介绍如何构建经典电路的拉普拉辛形式与量子紧束缚模型的映射,第3 节具体给出实现不同边界条件下非互易AA 模型的电路设计方案,第4 节和第5 节利用SPICE 分别模拟非互易AA 模型在周期边界条件下的能谱和能量缠绕数以及在开边界条件下趋肤与局域模式的竞争,最后一节进行总结.
2 经典电路的拉普拉辛形式与紧束缚模型的对应
任意经典电路组成的网络都可以用一个图(graph)来表示,其节点和边分别对应电路的连接点和元件[48,58,59].如由电阻、电感和电容(RLC)等被动元件组成的电路,元件各自的物性方程为

这里的V和I分别表示元件两端的电压差和通过元件的电流,(R,L,C)分别为元件的电阻、电感和电容.根据基尔霍夫电流定律,利用以上物性方程,可以得到图中每个节点关于时间t的微分方程:

其中,In(t)和Vn(t)分别代表电路节点n的外界输入电流和对地电压,这里用 (Rnm,Lnm,Cnm)分别表示从节点n到节点m(下标 g 代表接地)的等效电阻、等效电感和等效电容,以便描述更一般的具有非互易特性的元件,通常的被动RLC 元件为互易的,即RnmRmn ≡R,LnmLmn ≡L,CnmCmn ≡C.上述方程可以写成更紧凑的矩阵形式:

其中,I(t)和V(t)分别表示节点输入电流和对地电压的列矢量,(R,L,C)分别为等效电阻、等效电感和等效电容构成的系数矩阵,矩阵元分别为

对于微分方程(5),考虑具有固定频率ω的AC电流源I(t)及其电压响应V(t),其形式为
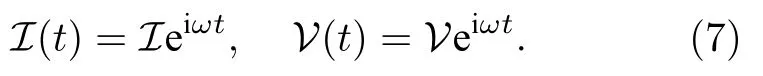
将它们代入方程(5),得到不含时的矩阵方程:
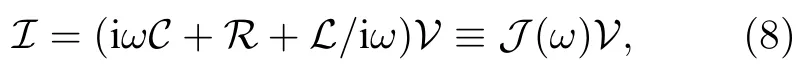
这里定义的J(ω)被称为电路的拉普拉辛矩阵或基尔霍夫矩阵[48],具有导纳的量纲,其矩阵元一般为复数,并且依赖于驱动频率ω.如果没有外界电流输入,即J(ω)V0,则 detJ(ωc)0 决定了电路的本征频率谱{ωc}.另外,也可以将(8)式的两边求逆,得

其中,G(ω)≡J-1(ω)被称为电路格林函数,具有阻抗的量纲.
实际上,对于具有(7)式形式的稳态解,任意电路网络都可以表示为拉普拉辛的形式,如包含放大器的主动电路[49,50,53]和具有非线性元件的非线性电路[60,61]等.
为了利用经典电路系统模拟量子紧束缚模型,可以将电路拉普拉辛矩阵J(ω)直接与紧束缚模型在实空间的哈密顿量矩阵H相对应[59],且拉普拉辛J(ω)的本征方程

可以直接对应哈密顿量矩阵的定态薛定谔方程.这里,jn(ω)为拉普拉辛矩阵的第n个本征值,构成本征导纳谱,可以完整模拟H的能谱.特别地,由detJ(ωc)0 可知,本征频率ωc使至少一个本征导纳为零,即jn(ωc)0 .由于J(ω)一般为非厄米矩阵,即J†(ω)(ω),相应的本征矢通常包含本征右矢和本征左矢利用电路的交流分析,可以得到J(ω)的右本征模式从而模拟H的右本征态;左本征态可以用J†(ω)模拟.通过元件以及驱动频率的设计和调节,J(ω)具有高度可控性,原则上可以模拟任意维度、任意边界条件、非线性和非厄米等非常广泛的量子模型的稳态性质.
接下来,应用以上电路的拉普拉辛形式构建J(ω)与非互易AA 模型哈密顿量矩阵H的对应关系,从而对其稳态性质进行模拟,包括周期边界条件下的能谱和缠绕数以及开边界条件下趋肤和局域模式的竞争.
3 非互易AA 模型的电路拉普拉辛
在交流驱动下,被动元件往往呈现出互易性,这是由最基本的基尔霍夫电流定律决定的,如电容与电感的导纳JC(ω)iωC和JL(ω)1/(iωL)均不依赖于正向或反向测量即可表征.而根据(8)式的描述,要实现拉普拉辛矩阵的非互易性Jmn(ω)(ω),则需要电路中某一元件的导纳值依赖于测量的方式,这通常需要引入主动元件,如电流型负阻抗变换器(INIC)[53].如图1(b)所示的INIC由放大器和若干线性元件构成,根据基尔霍夫电流定律,容易得出两端的输入电流分别为

图1 (a)上图: 非互易AA 模型的电路模拟示意图,包含 N 个有效电压节点 Vn (n=1,···,N),节点间元件 C0和I NIC(b) 模拟格点间的耦合,其中 I NIC(b) 用于实现关键的非互易耦合,其定义见图(b);接地元件 (L0,R0,C0,r,n)模拟格点的在位势;X相关模块和开关控制对不同边界条件的模拟.下图: X相关模块的定义.(b)I NIC 元件的内部电路图,由理想放大器、阻抗 Z±和目标元件 CI (没有 Xb )构成,可以实现 Vl,r 两端不同方向的导纳不同;I NICb 仅需将INIC 中的目标元件 CI 再并联一个 Xb 即可.(c)负阻抗模块[49],左右图分别实现对地单端口和自由两端口间的等效负阻抗 -Z,其中理想放大器上的标记表示输出电压与输入电压的关系.各元件的具体功能描述详见正文.Fig.1.(a)Upper panel: Sketch of an electrical circuit simulating the nonreciprocal AA model.It includes N voltage nodes Vn (n=1,···,N)with elements C0 and I NIC(b) simulating the intersite couplings,where I NIC(b) defined in panel (b)is the key element to realize the nonrecprocity,and the grounded elements (L0,R0,C0,r,n)simulating the on-site potentials;X modules and the switches control the simulation of boundary conditions.Lower panel: Definitions of X modules.(b)The internal circuit of the INIC,constructed by the ideal operational amplifier (opamp),impedance elements Z±,and the targeted element CI (without Xb),which can realize unequal effective input inductances from the two different ports Vl,r;I NICb is defined by adding an extraXb module in parallel with CI in INIC.(c)Modules of negative impedance[49].The internal circuits of the grounded one-port and the floated two-port negative impedances -Z for the left and right panels,respectively,where the labels of the ideal opamps represent the relation of the output voltage to the input voltages.See relevant texts for the detailed description of each element.

这表明一般情况下INIC 两端不同方向的导纳不相等:

为方便起见,理论上选取INIC 中的阻抗满足Z+Z-,使得元件两端流向放大器的电流大小相同方向相反,即IlIr,从而得到两个方向符号相反的导纳:Jl(ω)-Jr(ω).
另外,这里会用到具有负值的元件(如负电阻等),其两种实现形式如图1(c)所示[49],它们通过放大器分别实现了对地单端口和自由两端口的等效负阻抗(导纳).根据基尔霍夫定律,可得对地单端口电路(图1(c)左图)的输入阻抗为
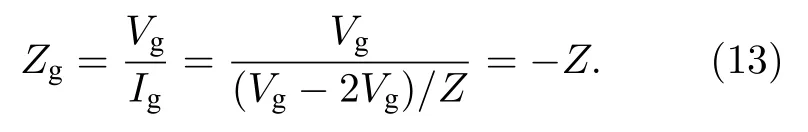
类似地,自由端口电路(图1(c)右图)两端的输入阻抗分别为
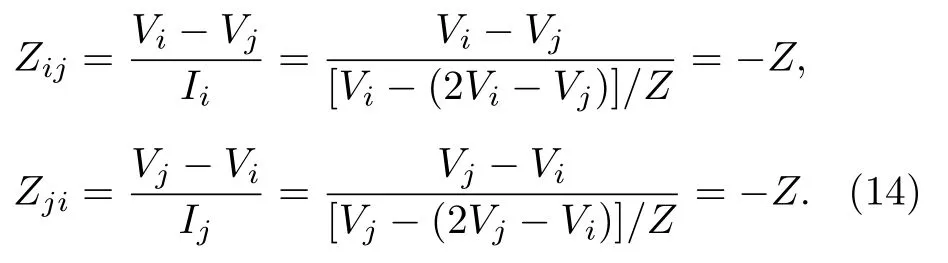
即,ZjiZij-Z.
利用以上关键元件,在由电感L0和电容C0组成的左手传输线离散模型(lumped-element circuit model for a left-handed transmission line)[62]的基础上,设计了如图1(a)所示的非互易AA 模型的电路模拟示意图,由RLC和INIC 等元件组成,包含有N个有效电压节点,对应模拟模型的N个格点.根据方程(8),容易写出此电路的拉普拉辛矩阵:

其中,
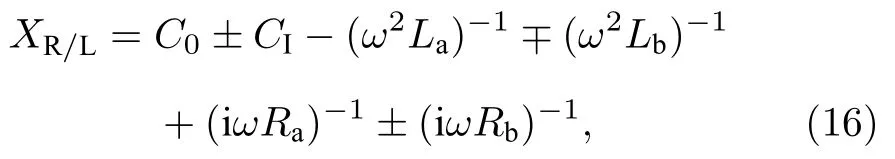
电容Cn,I、电感La,b、电阻Ra,b和R0在图1 中定义,E为单位矩阵;边界条件由图1(a)中 X相关模块与开关控制: 当两端的开关同时接入端口 o 并且 X相关模块(Xa,b和Xl,r)均开路时,系统对应于开边界条件;当两端的开关同时接入端口 p 时,下文中将会看到,通过 X相关模块参数的调节可以模拟具有磁通的周期边界条件.
将此电路的拉普拉辛矩阵(15)与非互易AA模型的哈密顿量矩阵(2)相比较,可以建立除D(正比于单位矩阵E)外两者间的映射A ⇔H,并利用对应的无量纲化参数得到如下等式关系.
对于电路的主体部分(不包含边界),由

可得
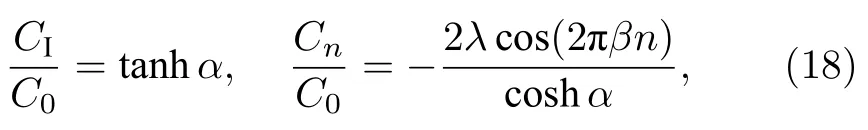
这里将C0作为参考电容.由此可以理解电路主体各元件的作用: (C0,Cr,L0)构成紧束缚模型的整体参考势((15)式中的D部分),C0还承担格点间互易耦合的作用,非互易耦合和变化的在位势由INIC 中的电容CI和接地电容Cn分别实现;随后可以看到,电阻R0和电容Cr的引入是为了使电路的响应不发散,它们仅使导纳谱在复平面内作整体平移.需注意的是,Cn随着节点n的变化会被要求为负数,等效负电容可以使用图1(c)的方案实现.
对于边界部分,同样利用对应的无量纲化参数关系

可得
4 周期边界条件下能谱和缠绕数的模拟
众所周知,即使在周期边界条件下,无序系统也不再具有平移不变性,因而无法通过将哈密顿量变换到动量空间的方法计算系统的缠绕数,而通常的办法是在链环中心加入磁通量为Φ的磁场,此时系统变为Φ的周期函数(周期为 2π),从而进行计算.对于非厄米系统,由于能量一般为复数,可以定义复能量在复平面的缠绕数来刻画非厄米系统的拓扑相[17,27]:
其中,θ(Φ)是detH(Φ)的幅角.对于非互易AA 模型,由文献[27]可知,不同的缠绕数表示不同的拓扑相: 在周期边界条件下,ν0 表示拓扑平庸的局域相,ν±1 表示两种拓扑非平庸的扩展相.
为了通过电路模拟并测量非互易AA 模型的缠绕数ν,利用两者的对应关系可以将定义(21)式中的H用拉普拉辛矩阵(15)中的A/C0替换(这里除以C0是为了保证 ln 等函数的作用对象是无量纲的,整体的倍数并不会影响ν的结果).因此,只要能从实验上测量出不同Φ下的A(Φ)矩阵,即可计算出相应的缠绕数.
本文利用电路的格林函数形式(9)进行SPICE模拟.对于具有周期边界(将图1 所示电路两端的开关均置到 p 端口)的电路,仅在第n节点接入频率为ω的AC 电流源,测量所有N个节点的电压响应,并除以输入电流强度,即可得到电路的格林函数矩阵G(ω)的第n列矩阵元;每个节点均操作一次,便可得到整个电路的格林函数矩阵.然后根据关系J(ω)G-1(ω)得出拉普拉辛矩阵以及相应的矩阵A[63].得到实验测量的拉普拉辛矩阵J(ω),就可以计算其导纳谱及相应的左/右本征矢量,以及由此定义的一切物理量,从而和理论相比较.
需要注意的是,上述分析是基于电路系统在AC 电流驱动下的稳态响应,即(7)式.而事实上,在驱动频率接近本征频率时,除了会产生明显的共振响应外,还会激发电路系统的其他本征模式,这类响应通常被称为暂态响应.实验上获得稳态响应的方法一般是进行延时测量,待暂态响应消逝后再使用锁相放大器实现对稳态响应信号的捕捉.而在周期边界条件下,非互易AA模型的本征能量会出现复数,相应地,此电路的本征频率ωc一般也为复数(图2(b)、2(c)左图),这就意味着此频率下的暂态响应会随着时间发散 (I m[ωc]<0)或衰减(I m[ωc]>0 ).对于以频率ω∈R 为驱动频率的系统,发散的产生不利于系统响应的稳定,因此必须考虑对暂态响应的抑制,这里通过选取合适的R0达到此目的.
可以采用无磁通(Φ0 )的电路(此时的A与ω无关)计算本征频率的虚部,从而估算出所需要的R0.将公式J(ωc)V0 写成本征方程的形式:

可以求出本征频率ωc满足

其中,rCr/C0;an表示矩阵A/C0的第n个本征值,在周期边界条件下一般为复数[27].因此,只要选取合适的R0以及Cr使所有本征频率的虚部都不小于0,即 m inn(Im[ωc,n])≥0,则系统的响应不会随时间发散.当系统以特定频率ω驱动时,系统的稳定响应将以ω模式为主[27].根据附录的推导,可以得出使电路响应不发散的条件为

另外,为了尽可能多地诱导出本征模式,驱动频率需要处于本征谱中间.由于非互易AA 模型H的能谱分布于复平面的原点附近,相应地,矩阵A(Φ0)/C0的本征值an也具有同样的特点,所以根据(23)式,设γan0 可以得到合适的驱动频率这样的取值同时可以保证(15)式中D尽可能简洁.除特别说明外,以下计算保持ω的取值.
利用SPICE 模拟周期边界条件下含有N21个节点的电路(图1(a)),基本的元件取值为(L0,C0,R0,Cr)(10µH,0.4µF,5 Ω,1.6µF),即ω00.5MHz和(r,γ)(4,1),驱动频率选为ω0.2 MHz,其他元件的取值(CI,Cn,La,b,Ra,b)根据(18)式和(20)式由模型参数确定,准周期势的周期参数选为β13/21 .利用以上方案,对理论相图(图2(a))中的3 个典型区域进行SPICE 模拟.在ν±1的拓扑区,模拟的A/C0本征谱在复平面内是绕原点的圈(图2(b)右图),而在缠绕数ν0的局域区,则变成了实轴上的直线(图2(c)右图);用模拟得到的A(Φ)/C0计算相位θ(Φ)detA(Φ)/C0随Φ的变化(图2(d)),可以得到相应缠绕数的模拟值.结果显示,模拟结果与理论结果符合得很好.
5 开边界条件下趋肤与局域模式竞争的模拟
文献[27]里证明了非互易AA 模型在开边界与周期边界条件下的相图一致,只是拓扑相区的态在开边界条件下表现出趋肤态,而在周期边界条件下表现为扩展态.本节将同样利用电路的拉普拉辛方法模拟开边界条件下趋肤与局域模式的竞争.
在电路的设计上,只需要将图1(a)中两端的开关同时接入端口 o 并且令 X相关模块均开路,即可实现开边界条件.同样地,可以利用与第4 节周期边界条件类似的方法,通过SPICE 模拟重构出开边界条件下的电路拉普拉辛矩阵以及相应的矩阵A/C0,然后用此矩阵计算出相应的本征左/右矢,即可看到趋肤和局域模式在不同参数下的竞争关系.这里将采用一个相对简单的方法,无须将AC 电流源依次接入每个节点也可以达到此目的.

电路的格林函数形式(9)可以用拉普拉辛的本征左/右矢表示为这里,趋肤或局域模式表现为本征左/右矢矩阵元的分布是趋向于一端还是局域在某个中间位置.可以简单地在单一节点接入AC 电流源,测量相应的电压响应,根据(25)式可知,此电压响应是同一相区下所有本征右矢按系数线性叠加的结果,所以必然表现为趋肤或局域效应.
取与周期边界条件时相同的元件参数,除了γ0 (即R0开路),这是因为开边界条件下所有的本征频率都是实数,如图2(b)和图2(c)所示,不存在响应发散的问题,所以不需要用电阻抑制发散.另外,需要拉普拉辛矩阵中的D(ω)0,否则当此项很大时,所有本征值jn(ω)趋向于常数j,由(25)式可知V →j-1I,其正比于输入电流,无法反映出竞争关系,这也是取γ0 的一个原因.
用SPICE 同样模拟了开边界条件下N21个节点的电路系统,在节点ni11接入频率为ω的AC电流源,然后测量每个节点频率为ω的电压幅值,得到如图3(a)和图3(b)所示结果,可以清楚地看出,在拓扑相区时,响应电压分布在右/左边界附近,表现为右/左趋肤态;在非拓扑相区时,响应电压始终分布在驱动节点附近,表现为局域态.为了表征相应电压的局域化程度,定义倒参与率(inverse participation ratio,IPR):

图3(c)和图3(d)显示IPR 最低的点与理论相变点很接近,因为趋肤和局域态都有较大的局域性,对应较大的IPR 值,而相变点附近扩展性最强,对应的IPR 值都很小.在左右趋肤的相边界(即ν±1之间的边界),对应于互易模型,因为趋肤效应消失,所以其本征态为扩展态;在趋肤与局域的相边界(即ν±1 与ν0 之间的边界),对应于趋肤与局域竞争的平衡,同样为扩展态.

图3 (a),(b)由SPICE模拟得到的电压响应(已经归一化)在节点上的分布,分别对应图2(a)中α=0.5和λ=0.5的两条虚线.频率为ω=ω0/的AC电流源接在第11个节点上.(c),(d)分别为由图(a)和(b)中的电压分布根据(26)式计算的IPR,其中菱形为模拟值,虚线为理论值,箭头指的是最小模拟值,虚线标出的是理论相变值.Fig.3.(a),(b)Node distributions of voltages (normalized)simulated by SPICE along dashed lines of α=0.5 and λ=0.5 in Fig.2(a),respectively.The AC current source with ω=ω0/ is connected to the 11 th node.(c),(d)IPRs of the voltage distributions in panels (a)and (b),respectively,calculated by Eq.(26),where diamonds (dashed lines)are the simulation (theoretical)results.The arrows indicate the minima of simulated IPRs,while the dashed lines indicate the phase transition points in theory.
6 结论
本文通过构建经典电路,将其拉普拉辛矩阵与非互易AA 模型的哈密顿量矩阵对应,利用SPICE成功模拟了非互易AA 模型重要的稳态性质,包括周期边界条件下体现系统非厄米拓扑性质的复能谱和能谱缠绕数,以及开边界下非厄米趋肤效应与准无序局域化的竞争.其中,详细讨论了电路参数的设置原则和理论依据,为进一步的实验实现提供了具体的指导方案.由于方案的普适性,本文所讨论的设计原则和理论可以直接应用于其他量子紧束缚模型的模拟和实验,如文献[27]中提到的非互易AA模型的对偶模型,仅需将图1 中的电路方案适当修改,去除节点间的INIC 元件以实现互易跃迁,并调节相应的接地元件以实现准周期复在位势即可.
本文中的SPICE 模拟使用了LTspice 软件.为了更接近于理论结果,采用的电容、电感和电阻均为理想线性器件,并且将INIC 中放大器的开环增益倍数与输入阻抗分别设置为 500 G和500 G Ω用于模拟理想放大器.由于实际器件的非理想性,模拟或者实验结果可能会有一定偏差,需要根据情况具体分析.
本文只涉及对量子紧束缚模型稳态性质的模拟,实际上,经典电路也可以用于对动力学性质的模拟.对于非互易AA 模型,文献[27]已有讨论.另外,由于电路元件的丰富特性,同样可以利用非线性的电路元件实现对非线性量子系统的模拟[64].所以,对于模拟量子系统而言,经典电路是一个成本低廉、技术成熟、模拟范围广的有力平台.
附录
根据本征频率的表达式(23),如使电路响应不发散,需要满足≥0,即


两边再平方并化简,得
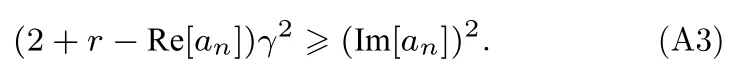
由于不等式右方为非负数,所以必须要求

且

因为需保证所有本征频率都满足以上条件,所以要求

