面向量子计算的拓扑超导体材料、物理和器件研究*

2022-08-28姜达余东洋郑沾曹晓超林强刘伍明2

物理学报 2022年16期

姜达余东洋郑沾曹晓超林强† 刘伍明2)‡

1)(浙江工业大学理学院＆前沿交叉科学研究院,杭州 310014)

2)(中国科学院物理研究所,北京 100190)

鉴于“摩尔定律”已经逼近极限,众多替代传统计算的方法被提出,其中量子计算是最受关注和研究最广泛的一种.由于量子体系的不可封闭性,外界大量不可控的因素会导致量子耗散和退相干,为了尽可能避免量子叠加态的退相干,制备具有鲁棒性的量子比特成为了关键环节之一.马约拉纳零能模是拓扑和超导复合体系中涌现的准粒子,具有非阿贝尔统计性质,它的时空编织受到非局域的拓扑性质保护,因此,以马约拉纳零能模构造的拓扑量子比特对量子退相干具有天然的鲁棒性.虽然经过全球范围内各个实验组艰苦卓绝的探求,目前关于马约拉纳零能模的实验验证仍然扑朔迷离.本文回顾了量子计算的发展历程和主要的技术手段,重点介绍了拓扑超导态/体的理论、可观测的实验现象、以及最新的实验研究进展,并对此做出了分析和评述.最后对拓扑超导态/体在量子计算领域的应用前景进行了展望.

1 引言

1.1 何为量子计算

信息是现代科学的一个核心基本概念,它已影响到生活的各个方面.在经典信息论中,信息的内容和形式以二进制方式加载在一连串的确定状态0 或1 上.由于内容和形式可以有不同的表达,现代科学更关心信息的度量,而非信息本身的价值.信息量的基本单位是比特(bit).计算(compute)在拉丁语里由“com”和“putare”构成,指的是处理信息并将其简化为数据.量子计算,相对于经典计算而言,是指计算的物理实现遵循的是量子物理的规律,而非经典物理的规律.因此,在计算过程中量子计算会用到量子物理的非经典性质,如态的叠加、纠缠、非局域性等.一般情况下,量子态不可进行克隆,测量也将导致量子态坍缩.这两个事实使得量子计算过程中往往无法进行复制和反馈,这也意味着量子计算和经典计算必然存在巨大的差异.

对照经典计算,量子计算也可分为软件和硬件两大部分: 软件部分包括算法分析和设计、量子编程语言、软件等;硬件包括量子芯片、量子存储器等.从处理信息的形式来分,量子计算又可分为离散变量型和连续变量型.量子计算也可从计算模型角度来区分.在众多的计算模型中,当下最受学界重视的方案有量子门阵列、单向量子计算、绝热量子计算和拓扑量子计算等四种.

尽管量子计算领域发展快速,但受限于量子计算的理论研究,人们尚不知道量子计算机的最终设计方案.需指出的是: 目前所谈论的量子计算机往往指的是对特定问题能达到指数级别加速的处理器,而非一个独立完成计算任务的装置设备;相应地,目前所谈的量子计算其实是一种异构运算,它将需要加速的代码在量子芯片上执行并返还给经典计算机协同完成计算任务.

1.2 量子计算的意义

由于对数据处理量和计算速度要求的不断提高,芯片的集成度不断提高,运算产生的热已限制元件的性能和寿命.尽管多处理器和分布式计算能部分缓解该方面的压力,但无法从本质上克服困难,也无法降低计算的能耗.目前智能手机3 nm芯片即将进入使用,在该尺度及更小的尺度下,经典物理的规律将不再准确,必须考虑量子效应.因此,基于量子规律的量子芯片、量子存储器设计方案,以及相匹配的计算方案自然地成为了普遍关注的科学问题.

由于用于计算的量子态可以和电位的高低没有关系,量子比特位诸如翻转等演化没有产生焦耳热的机制,原则上讲,量子计算元件密集程度(性能和寿命)应不受散热条件的限制.

经典计算使用确定的宏观状态0和1 进行运算.量子计算,以离散变量型为例,则以复Hilbert空间的微观量子比特(qubit)计算基矢|0〉和|1〉进行处理.与经典物理不同的是,量子态一般处在这两个基矢的叠加态上.一个位上的量子态,以Bloch球来表示,其分布可布满整个球面,而|0〉或|1〉则为球面的两个极点.由此可知,一个qubit 可以有无穷多种存在方式,这意味着量子计算具有高度的并行性和几乎无限的信息承载能力.具体地说,由于一个经典的二进制存储器只能存储0 或1 中的一个数,n个经典的二进制存储器只能存储2的n次方个排列中的一个数,而由于量子叠加原理,n个量子二进制存储器可以存储2n个排列的所有的数.可见,量子存储器的容载量是呈指数增长的.当n很大时,比如n=275,量子存储器可存储的数据量比宇宙中的原子总数(上限约为1082个)还要多.由此可知,基于经典物理原理设计的存储器无法胜任很大规模下的信息处理.此外,由于哈密顿算符是线性算子,量子叠加态的演化是并行的,且相互间不需要进行通信.同样地,由于态叠加原理,在各个量子比特位上可以同时进行多个数据的写入,或者同时进行多个数据的读出.因此,量子计算的高并行性特点原则上可展现出更快的计算速度.再考虑到量子比特间的纠缠等特性,一些特殊制备的量子源在特定问题上,有着超越经典计算机方案的处理速度和能力.

量子计算未来有十分巨大的应用前景,尤其在与大数据量相关的一些研究和应用上,比如:

1)大数据科学.使用量子计算可以更全面、快速、准确地找到需要的海量数据检索,用于检索商业信息,方案的优化,信息的整合和预测,比如便捷的线上贸易、私人定制的(健康、金融等)信息服务、投资组合优化和风险预测、犯罪分子的快速发现和追踪.

2)量子模拟.工业生产前期往往需要利用行业软件进行大规模高精度的模拟,当前的模拟对软硬件要求很高,但仍无法得到很高的精度.使用量子计算有望在更大的规模、更长的演化时间上来研究相关的工业过程,得到更精确的结果,因而能带来巨大的经济效益.比如,应用量子计算改善催化剂,用于实现高效无害高质量的生产方式来生产氯乙烯和氨肥(或对应替代物),则分别对绿色环保和粮食增产起到重要作用.从科学和新技术角度来看,量子计算在化学合成、高分子新型药物的研制、生命现象等领域将发挥巨大的作用.比如,医学技术水平有望进入到原子、亚原子级别;意识和生死,作为涌现现象,有望通过大规模的模拟来进行初步地研究.

3)人工智能.量子计算有助于提高机器学习的广度、速度和复杂度,提高视觉识别、语音识别、模式识别等来模仿和实现更复杂的人类智能行为,进而执行更为复杂的任务,比如地道的语言翻译、准确的医学诊断、严格的数学证明、有效的危险识别和规避等.得益于更快的计算速度,人工智能有望对一些微观物理化学过程进行"实时"反馈和调控,提升人类对微观粒子的操控能力.

4)数字主权及安全.数据在现代社会中起着重要作用,数据的安全性是大家十分关心的问题.比如密码学的基本工作原理是大数分解成两位大质数的乘积,由于高的计算复杂度,经典计算要找出结果需很长的时间,而量子计算的高度并行性使得计算在极短的时间内就可以完成,因此,量子计算的成熟应用必然要求彻底改变现代密码系统,尤其是涉及敏感信息的国防系统和金融系统.同样地,数字货币也可能需用更安全的量子数字货币代替.基于量子计算的安全协议变得十分重要.考虑到通信的绝对安全性,结合量子计算的高度并行性,量子计算用于网络时,可能使得网络攻击呈现范围大,攻击密集,实时性强等特点.无论是进行网络攻击和防御的手段,对国家安全而言都是重要的.

1.3 量子计算的发展历程

20 世纪初,随着对微观世界的探索发现,量子物理在争议声中快速发展,人们认识到微观世界的规律,可以完全不同于经典的经验;同一期间,Gödel,Church和Turing 提出三种计算模型,带动了数字电子计算机的高速发展.通过对非传统计算方法开展研究,后来人们认识到: 这三个模型都包含了与计算量相关的不合理的物理假设,即某些物理过程并不能通过计算模拟出.1970 年,Park[1]提出量子态不可克隆定理,该定理在1982 年被Wootters和Zurek[2]重新发现.1973 年,Bennett[3]提出了可逆图灵机的方案.

1980 年到1999 年期间,科学家主要在理论方面开展研究,侧重点是量子逻辑门(CNOT 门,Fredkin 门),量子图灵机和一些算法的方案.其中比较著名的有: 1980 年,Benioff[4]基于可逆图灵机提出了量子图灵机模型,Manin[5]也提出了量子计算机的想法.Feynman 在1981 年建议建造量子计算机,在1982 年指出所有经典计算机模拟量子系统都存在指数变慢的现象,而基于量子原理的模拟器则可能无此变慢.1985 年,Deutsch 提出了第一个通用量子计算机模型.1992 年,Deutsch和Jozsa[6]提出了指数加速的Deutsch-Jozsa 算法.1993 年,Bennett等[7]提出了量子隐形传态方案.1994 年,Shor[8]提出了Shor 算法,在量子计算机上该算法对于大数分解的计算速度远远快于表现最好的经典算法.1995 年,Monroe等[9]用俘获的离子首次实现CNOT 门.1996 年,DiVincenzo[10]提出了构建量子计算机的若干判据;Grover[11]提出了一种以平方幂次加速的量子搜索算法.1997 年,Kitaev[12]提出拓扑量子计算的方案,该方案可有效地对抗退相干.1998 年,第一个量子计算机(2 比特NMR 量子计算机)诞生,并在其上成功实现了Deutsch 算法[13];Omer 提出了量子计算编程语言.

2000 年以后,量子计算在理论和实验方面都开始有了突破.2000 年,Pati和Braunstein[14]证明了量子不可删除定理,它表明量子信息既不能被制造也不能被销毁.2001 年,基于单光子的光学量子计算模型[15]和基于测量的量子计算模型[16]出现.2003 年,Pittman[17]和O’Brien[18]两个组独立地演示了基于线性光学元件的量子CNOT 门.2004 年,科学家实现了量子隐形传态[19].2005 年,Chanelière等[20]演示了两个量子存储器间信息交换.2007 年,单原子单光子服务器出现[21].2008 年,基于量子光学频率梳的大规模量子计算方案出现[22].2009 年,Lloyd等[23]提出HHL 量子算法,对于求解线性系统能达到指数加速效果;Schoelkopf等[24]制造了第一个固态量子处理器;O'Brien等[25]制造了光子芯片,并演示了15=3× 5 的Shor 算法;首个面向原子光学开发的拓扑簇态量子架构出现[26].

自2010 开始,量子计算从软、硬件两方面都得到了快速的发展,众多芯片方案均在实验上得到了验证,商用的量子计算机也被制造出来.2010 年出现了双光子芯片[27].2011 年,14 比特的量子注册机[28]制造了出来;Aaronson等[29]提出了玻色采样理论方案;D-wave 制造并售出了量子淬灭机.2012 年,世界第一家量子计算软件公司1 QB 量子技术成立.2013 年,量子态可达到小时级别的相干时间[30,31].2014 年,基于钻石的大规模量子计算架构方案[32]出现;基于隐形传态技术,科学家实现了高保真、米级的数据传输[33].2016 年,在基于离子阱的量子计算机上实现了Shor 算法[34],IBM 开放了量子云计算平台Quantum Experience[35],Google利用9 个超导比特对氢气分子进行了量子模拟[36].2017 年,科学家在微芯片上产生了两个纠缠的比特,共含100 个态分量(每个比特上有10 个态分量)[37];微软发布量子编程语言Q Sharp;第一个用于商业量子计算机的用户交互式操作系统出现;反事实量子通信方案通过实验验证[38],量子信息交换有望不通过携带者或隐形传态方式直接完成.2018 年,三光子态用于加速量子计算[39];硅基双比特量子处理器通过测试[40];用于连续变量量子信息处理的集成光子平台出现[41];IonQ 公司制造了基于离子陷俘的首台商用量子计算机.2019 年,IBM制造了它的第一台商用量子计算机,奥地利科学家在量子计算机上模拟了晶格模型[42];谷歌声称量子计算机实现了量子优越性;IBM 研制出了53 个qubit 构成的量子计算机;潘建伟团队实现了多光子玻色采样[43].2020 年,科学家提出并给出了一个量子布线问题的解决方案[44],对纠缠声子对进行测量后实现了测量信息的量子搽除[45],利用谷歌公司的量子求解器研究了氢链的结合能和二氮烯的异构机制[46],在城际级别实现了8 用户量子通信网络[47].潘建伟团队使用(峰值为76 个光子比特)九章玻色采样机实现了量子优越性[48].2021 年,中国科学家建立了世界最大的综合量子通信网络,实现了地面和卫星的连接[49];在无人机间成功传输了纠缠的光子,标志着量子网络的研究进入可移动的阶段[50];制造出了目前世界上最强的量子计算机祖冲之2,它是一台66 比特可编程超导量子计算机.国外研究人员展示了用于分布式量子计算机的第一个量子逻辑门的原型[51];奥地利、德国和瑞士的研究人员展示了两台19 英寸机架的量子计算演示器[52].在量子比特数目方面,研究也取得了较大突破: 可编程的量子模拟器可操作的量子比特数达到256个[53],基于Rydeberg 原子的量子模拟器的原子数也达到196个[54].另外,滑铁卢大学利用量子计算机对重子进行了模拟[55].到目前,量子计算的各个方面都在蓬勃发展.

2 量子计算的理论基础

2.1 量子比特

比特是计算的基本单位,在传统计算机中,一般用低电平0和高电平1 编码二进制数据位.类似地,在量子计算中,其物理对应可以是任意的一个二能级比特体系,比如把低能级标记为|0〉态,高能级标记为|1〉态.一个量子比特,即量子双态系统组成的态矢空间,就是一个二维Hilbert 空间.理论上一次量子操作可以同时实现2n个叠加的数据进行并行运算,这相当于电子计算机进行2n次操作.基于量子力学的量子计算提供了一种从根本上实现并行计算的模式,具备远超过经典计算机运算能力的前景.

值得指出的是,传统图灵机的架构同样适用于量子计算,可以对量子比特执行可编程的逻辑操作,实现通用的量子运算,从而获得计算能力的指数级加速提升.作为比较,每秒运算万亿次的电子计算机对一个300 位的大数质因数分解需要10 万年以上,而利用同样运算速率、采用数学家Shor提出的量子分解算法的量子计算机只需要1 s[8],这对经典信息安全体系将带来深远的影响.

2.2 叠加态

经典计算机中每个比特只能表示0 或者1 中的一种状态,经过逻辑门运算之后得到的结果也是如此.对于量子比特而言,遵循量子力学的定律,不仅可以是|0〉态或|1〉态,也可以是|0〉和|1〉的任意线性叠加态:α|0〉+β|1〉,其中α,β都是复数,且满足归一化条件|α|2+|β|2=1.一个量子比特可以同时包含|0〉态和|1〉态的信息,这体现了量子力学中特有的相干性.目前单量子比特可以用Bloch 球表示,如图1 所示,多量子比特则用张量乘积来描述.根据Feynman 关于态叠加原理的解释,如果一个系统处在叠加态,在不破坏这个态的前提下,原则上没有任何物理手段可以确定或区分在这个态中系统究竟处于|0〉态还是|1〉态.量子体系与外界环境的作用会导致叠加态的分布和相位信息丢失,使编码量子态退化为经典态,即量子退相干现象,这是目前量子计算遇到的关键难题.

图1 经典比特(左)和量子比特(右)图示.量子比特可以代表|0 〉态和|1 〉态的叠加态Fig.1.Classic bit (left)and qubit (right).Qubit presents the superposition of |0 〉and |1 〉 .

作为态叠加原理应用在多体量子系统时的特有性质,量子纠缠代表不同体系之间的非局域、非经典关联[56],在数学上表现为复合系统的量子态无法写成子系统之间的直积.目前光子纠缠源的产生有两个主要方法: 基于自发参量下转换技术[57]和单个原子自发辐射产生的确定性单光子[58],纠缠光子在量子通信及量子计算中有着重要的应用价值[59,60].

3 实现量子计算的主要技术路线

3.1 超导体

超导体是实现量子计算的又一条有效技术路线,是通过超导系统的量子态来实现量子计算[61].超导量子计算的一个重要优势是与现有的半导体工业技术兼容,可以在技术上很顺利的从传统计算过渡到量子计算,而它的劣势则是需要在低温下才能工作.

在超导电路中实现量子比特的基本元器件是具有非线性特性的约瑟夫森结(Josephson junction),它是两个超导体之间夹一个绝缘体薄层的三明治结构(如图2 所示).在超导态时,库珀对可以隧穿绝缘层造成的势垒形成超导电流,这就是约瑟夫森效应,这里的超导电流满足以下两个方程:

图2 约瑟夫森结示意图.Fig.2.The schematic of Josephson Junction.

其中I是流经约瑟夫森结的电流;Ic是临界电流;φ是绝缘层两侧超导体的相位差;V是两侧超导体的电势差;Φ0h/2e是磁通量子.这就是约瑟夫森效应方程.由约瑟夫森效应方程(1)和方程(2)可以推导出约瑟夫森结本身存储的能量:

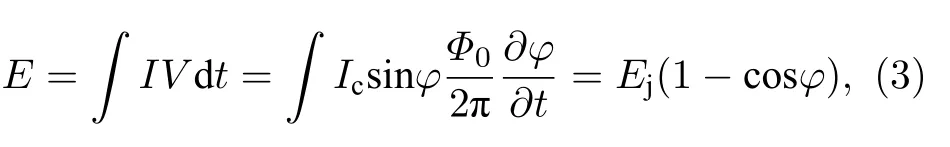
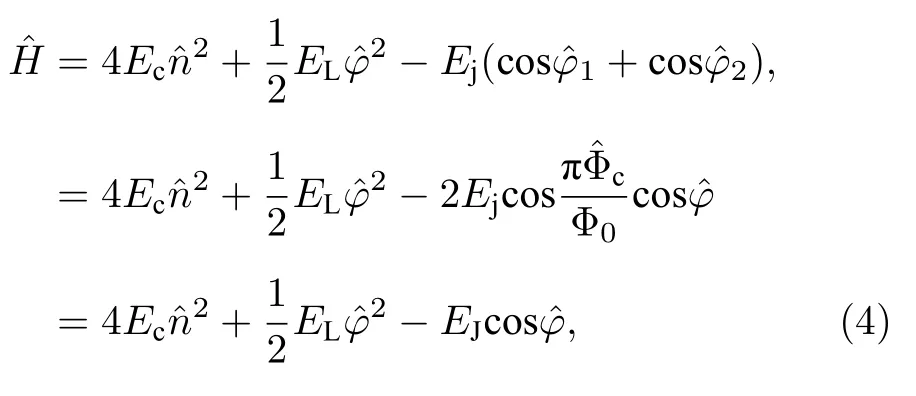
从约瑟夫森结的哈密顿量出发,基于约瑟夫森结的电路可以设计出三种量子比特结构: 电荷量子比特 (charge qubit)、磁通量子比特 (flux qubit)及相位量子比特 (phase qubit).

电荷量子比特当Ec≥EJ时,电荷能量占据优势,电感可以忽略,超导体中的库珀对数目可以作为量子比特的量子态,这种类型的量子比特称为电荷量子比特,也称为Cooper-pair box[62].

磁通量子比特当EJ＞Ec时,电容可以忽略,电路由电感和约瑟夫森结组成,通过磁场调节约瑟夫森结的中间势垒高度,改变约瑟夫森结两边势阱的最低能级跃迁,产生两个超导电流方向,分别对应着量子比特中的|0〉和|1〉量子态,这种类型的量子比特称为磁通量子比特.

相位量子比特当EJ≫Ec时,与磁通量子比特类似.通过外加直流偏置电流,使得势阱中只存在几个有限的能级,将最低两个能级作为量子比特的|0〉和|1〉量子态,这种类型的量子比特称为相位量子比特.

超导量子计算中所用到的超导体分为两大类,一类是以铝为代表的传统超导体;另一类是存在马约拉纳准粒子的拓扑超导体.

3.1.1 传统超导体

谷歌、IBM、英特尔、本源量子、浙江大学、南京大学、北京量子信息科学研究院等国内外企业和科研机构采用的是传统超导体来实现量子计算的技术路径.2019 年美国谷歌公司研制的53 个量子比特的Sycamore 处理器首次实现了“量子优越性”[63],制备该处理器的材料是生长在硅片上的常规超导体铝膜,通过紫外曝光和电子束曝光进行14 次光刻过程完成,该研究成果具有里程碑式的意义;2021年,中国科技大学潘建伟院士团队推出了62 个量子比特的超导处理器“祖冲之号”[64],该处理器同样也是利用传统超导铝模制备,通过Al/AlOx/Al 结构来制备约瑟夫森结,从而实现量子比特;同年,浙江大学也发布了利用传统超导体铝模制备的“莫干1 号”和“天目1 号”超导量子芯片学术成果[65].传统超导量子计算已经逐渐成为实现量子计算的主要技术路径之一.但是传统超导量子计算存在一些无法忽视的问题,除了需要在低温下工作外,由于量子体系的不可封闭性,外界大量不可控的因素会导致量子耗散和退相干,即量子叠加态的坍塌,因此传统超导量子计算机的相干时间较短,远短于用光学方法制备的量子计算机.

3.1.2 拓扑超导体

为了尽可能避免量子叠加态的坍塌,制备稳定的量子比特成为关键环节之一.解决这个问题的一个有效方法就是使用马约拉纳零能模构造的拓扑量子比特.马约拉纳零能模只在具有非平庸拓扑的超导体中可能出现,然而,目前关于拓扑超导体的研究面临理论不完善、材料工艺要求奇高、制备复杂、探测手段匮乏等困境.微软、荷兰代尔夫特大学、清华大学、北京大学、中国科学院物理研究所等国内外企业和研究机构都在拓扑超导体中尝试基于拓扑量子比特的量子计算路径.目前,关于拓扑超导态和拓扑超导体的理论研究已经非常丰富,在超导异质结和拓扑超导体等体系都观察到了马约拉纳零能模的间接信号,新的拓扑超导材料研发及其器件的制备等仍然有待进一步提高.在后面的第4、第5 章节将详细介绍面向量子计算的拓扑超导体理论和实验上可观测的现象;第六章将详细介绍目前面向量子计算的拓扑超导体材料的实验研究进展.

3.2 半导体

硅基半导体集成电路技术是现代工业文明的基石,据此发展起来的技术和工艺丰富多样,因而与现代硅基半导体集成电路技术兼容的半导体量子点量子计算方案始终受到广泛的关注.根据研究,为了实现能够容错的量子计算,单比特和双比特的相干时间(退相干时间)要尽可能的长,而操控时间要尽可能的短,它们成为衡量一个量子计算平台的两个重要物理指标[66].早期的半导体量子计算研究利用电子的自旋作为量子比特,主要材料是Ⅲ/Ⅴ主族材料体系[67],如GaAs 量子点,InSb 纳米线等.由于受到材料核自旋的超精细相互作用的随机影响,这些异质结中的电子自旋量子比特退相干时间都较短,使得在半导体工艺中构造高保真度量子比特困难重重.近年来,基于Ⅵ族的Si和Ge材料得到了迅速的发展,尤其是同位素纯化技术使得人们能够制备出无核自旋28Si和72Ge 的量子点,配合诸如动力学解耦脉冲(dynamical decoupling pulse)等技术,人们大幅提高了半导体中的量子比特的相干时间.类比于经典计算机,量子计算机的任意程序也可以分解为有限次的逻辑量子比特的连续操作,比如三个单量子比特Hadamard 门,Pauli-Z 门和T 门,以及一个让两个量子比特纠缠的双比特门,如CNOT 门或门或CZ 门等[68].但是,由于不可避免的耗散和环境相互作用,半导体量子点平台的量子比特始终具有有限的保真度(fidelity),微弱的错误会在后续的计算中叠加和累计直到量子比特完全被损坏.一种基于纠错码的容错量子比特方案即Surface 码在2012 年提出,该方案指出只有单比特门和双比特门的保真度均超过99%时才能够构造一个大规模的量子计算平台[69].

其中ω,ω0γB0和ωRγB1分别是微波脉冲、拉莫尔和拉比频率.基于自旋的量子比特读取需要通过自旋/能量依赖隧穿或者自旋阻塞实现自旋-电荷转换,从而读取自旋量子比特.比如通过自旋/能量依赖隧穿技术,人们实现了对硅附近束缚电子自旋的单次读取[71].自旋阻塞效应需要辅助量子比特协助以实现对量子比特的读取,Harvey-Collard等[72]借助charge-state latching 技术实现了99.86%的受控测量保真度.半导体材料如29Si 的超精细相互作用的随机涨落会导致其中的量子比特相干时间很短,通过使用同位素纯化(28Si)以及电偶极自旋共振等技术,2017 年Yoneda等[73]实现了退相干时间20 µs,操控时间17 ns,受控保真度达到了99.6%的良好成绩.而自Kane 提出Si:31P系统核自旋可以用作量子比特以来,Si:31P 系统得到了深入的研究,2014 年Muhonen等[74]实现了99.99%的受控保真度以及达600 ms 的退相干时间.除了使用自旋量子比特以外,人们也使用电荷,自旋-电荷杂化系统作为量子比特,相关的研究都取得了很好的进展.

双比特量子比特门主要依靠三种方式耦合两个单量子比特而实现,包括交换相互作用(近邻,次近邻等)、库伦相互作用以及腔量子电动力学,特别地,交换相互作用因为控制简单而研究最多.近年来,一种新的双比特门—“CROT 门”—得到了深入的研究,它结合了CNOT 门和一个单比特门,而且它不需要操控交换相互作用的强度便能实现一次CROT 门操作,有效减少了环境噪声的影响.在2018 年,Huang等[75]实现了CNOT 门高达98%的保真度.Gate-set tomography 技术能够将Hamiltonian error和随机错误分离,因而使得人们能够纠正控制错误、门依赖错误等,从而提高保真度[76].2022 年初,三个小组同时报道了单比特门和双比特门均超过99%临界保真度的小规模量子点量子计算系统,包括在磷31P 掺杂的28Si 材料中实现的1 个电子2 个核自旋量子比特系统[77]、同位素纯化的硅基半导体量子点[78]和同位素纯化的28Si/SiGe 异质结[79],此三项工作标志着半导体量子计算迈上了新的台阶.继续优化和发展制备、操控和测量等工艺和技术,进一步实现可扩展的更大尺度的量子点量子计算系统便成为下一步最为紧迫的方向.

3.3 光学

近20 余年来,基于量子光学的量子计算方向获得了很多有意义的进展,涉及的物理系统主要包括离子阱[80]、腔QED 系统[81]、极性分子系统[82]、光晶格[83]等.离子阱的特点是与外部环境耦合较弱,相干时间长,并且在量子比特的光学读取上具有很大优势.光学腔QED 利用原子与腔场的相互作用控制原子内部状态,以光子作为飞行量子位进行量子计算.极性分子体系则集合了中性原子与离子的特点,它通过微波控制量子位翻转,不影响双光子拉曼过程中激发态的布居,由于分子间偶极相互作用远小于离子间的库仑力,更容易俘获操控.在光晶格系统里,通过调节激光场可以操控占据同一格点的玻色子之间的相互作用强度及其在不同格点之间的隧穿概率.2002 年,慕尼黑大学的Greiner等[84]利用光晶格体系模拟了从超流态到Mott 绝缘态的相变,成果被量子物理专家Cirac和Zoller[85]认定为量子计算的首次实际应用.2021 年,清华大学的段路明研究组[86]通过精确调控施加在一维光晶格中的超冷原子所在位置的磁场,首次在实验上实现了量子中继协议中的两个中继模块间的高效纠缠连接(见图3).2022 年初,麻省理工学院物理系的Hartke等[87]利用激光干涉形成二维网状势阱,捕获了大约400对冷原子,并成功在每个钾原子对中观测到了两种不同量子振荡行为的叠加态,这是一种全新的量子比特.芝加哥大学的Bernien 团队[88]设计了一个由中性铷原子和铯原子构成的原子阵列,实现了首个由512 个量子位组成的中性原子体系.两种元素可以分别用作量子存储器和量子计算,扮演计算机中的RAM(随机存取存储器)及CPU(中央处理器)角色,对新的量子协议具有重要启发意义.

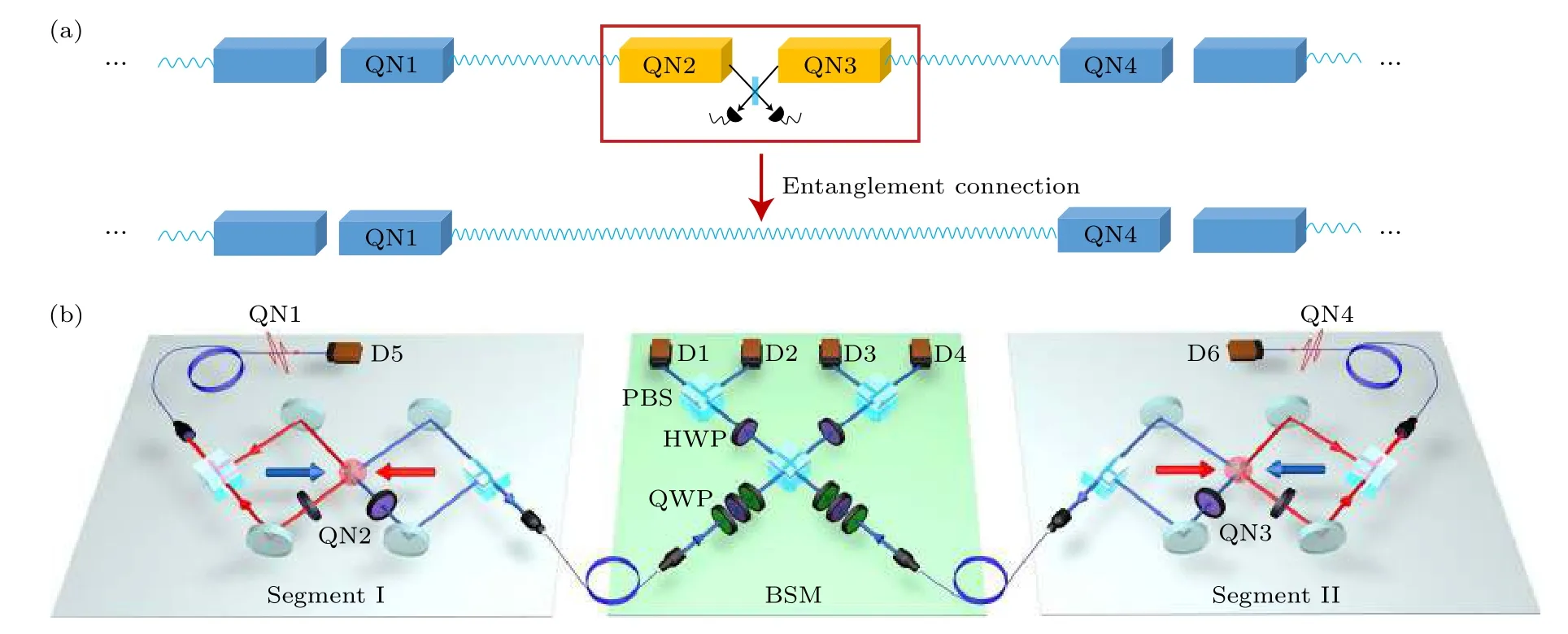
图3 (a)量子中继协议中的纠缠连接示意图[86];(b)量子中继模块之间的纠缠连接的实验系统示意图[86]Fig.3.(a)A sketch of entanglement connection (swapping)in the quantum repeater protocol[86];(b)the whole experimental set-up[86].

光子是传递电磁相互作用的玻色子,该“飞行比特”作为量子处理单元的物理载体和“链接”多个量子系统的桥梁,优点是抗环境噪声干扰能力强,是实现长距离量子网络和分布式量子计算的最佳载体,缺点是调控手段相对复杂.目前,科学家们已经成功利用光子的偏振[57]、路径(透射路和反射路)[89]、轨道角动量[90]、频率[91]等自由度作为量子比特编码.基于现有的光量子比特的制备和操控技术[92],国内外学者们先后展示了特定功能的量子计算平台.2013 年,意大利、英国、奥地利、澳大利亚等四个国家的研究团队分别采用单光子源和集成光学芯片展示了3 光子玻色采样[93-96].2017 年,中国科学技术大学的潘建伟研究组[97]利用一种共振激发的量子点单光子源产生的高品质光子,首次在国际上实现5 光子玻色采样(见图4).2018 年,上海交通大学的金贤敏团队[98]利用“飞秒激光直写”技术制备出节点数达49×49 的光量子计算芯片,创造了当时的世界纪录.2021 年,日本科学家Kashiwazaki等[99]研制出新型光纤耦合量子压缩光源,标志着人类向通用计算机的目标迈出了坚实的一步.

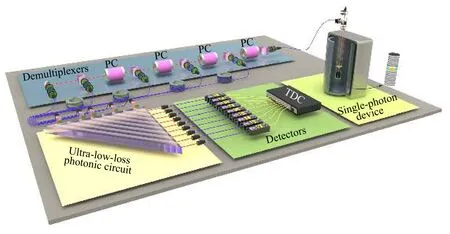
图4 多光子玻色采样实验装置图[97]Fig.4.Experimental set-up for multiphoton boson-sampling[97].

目前光量子计算机在解决特定问题时的计算速度已经远超经典计算机,在相关实用前景还需要进一步验证.光量子计算的优势是信息存储相对容易,另一方面,它面临的关键技术难点是高品质纠缠光学的制备和光子多自由度调控技术,光量子比特和其他系统之间的相互耦合也存在一些挑战.此外,光子数解析探测器及光学芯片制造技术也决定着光量子计算机的应用前景.

4 面向量子计算的拓扑超导体理论

4.1 粒子-空穴对称

凝聚态物质的主要组分是电子,电子是自旋为1/2 的费米子,并满足狄拉克-费米统计,即每一个量子态只能最多占据一个电子,因此,自由电子气的基态将是电子从低能到高能依次填满的费米海.在传统的Bardin-Cooper-Schrieffer(BCS)超导理论中,晶格的声子元激发能够在电子之间间接诱导微弱的吸引相互作用,该吸引相互作用导致费米海表面附近(费米面)的电子失去稳定性,形成无数的Cooper 对,从而形成超导现象.超导体的单粒子激发需要破坏Cooper 对束缚态,将电子从费米海内“踢出”去,即一个“空穴型”元激发和“粒子”元激发同时产生,粒子型元激发带正电,空穴型元激发带负电,因此,超导体的单粒子激发是粒子型元激发和空穴型元激发的相干叠加并呈电中性,超导体一般具有粒子-空穴对称性(PHS).粒子-空穴对称性显著地改变了凝聚态物质的拓扑性质,使得在一、二和三维都能够存在拓扑非平庸的拓扑超导体.特别需要指出的是,开放非厄密系统成为近年来的研究热点[100],北京师范大学Zhao等[101,102]和Jing等[103]研究了非厄密Kitaev 链,他们发现非厄密特性会破坏粒子-空穴对称性,从而导致非厄密系统的马约拉纳零能模显著区别于厄密系统,比如不完全马约拉纳零能模等.下面我们简单介绍单带常规超导体(厄密系统)中的粒子-空穴对称性.

众多电子构成的多体系统可以由以下哈密顿量描述:

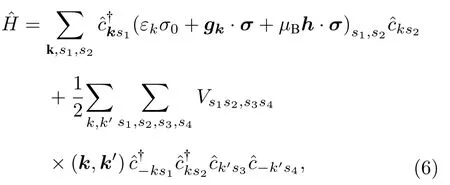
其中第一项是电子的单粒子性质,包括动能εk(如二次抛物型εkℏ2k2/2m*,m*为电子有效质量)、自旋轨道耦合效应gk·σ(spin-Orbit coupling,如二维体系中的Rashba型kxσy+kyσx),以及磁场h诱导的塞曼能等;第二项描述了电子之间的有效的相互作用,它们包括电子之间的库伦相互作用、由晶格振动以及反铁磁涨落等引起的有效吸引相互作用等.在BCS 理论中,假设对关联效应较弱,平均场近似依然较为准确,得到Nambu 表象下的平均场哈密顿量:

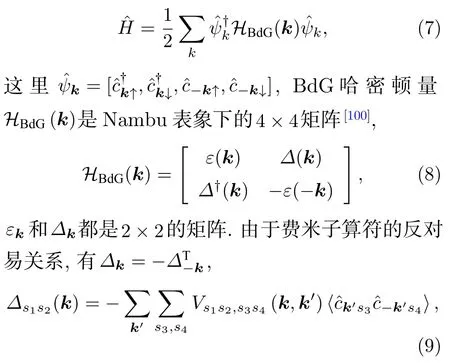
上述哈密顿量能够被波戈留波夫变换HBdG(k)[uj(k),vj(-k)]TEj(k)[uj(k),vj(-k)]T所对角化,其本征谱为Ej(k).定义粒子-空穴变换,

其中 12×2是2×2的单位矩阵,是厄密共轭算符.HBdG(k)在该粒子-空穴变换下有如下关系,

4.2 拓扑超导与马约拉纳准粒子

根据一般的拓扑理论,在没有特殊对称性(如时间反演对称性、中心反演对称性等)的情况下,一维和三维是不能够支持拓扑非平庸的拓扑物态的[104].但是,正是粒子-空穴对称性的出现,它显著改变了拓扑物态的性质,使得在一、二和三维都能够定义拓扑非平庸的物态.比如,在一维情形下,Kitaev于2001 年提出了一个最简单的无自旋p 波超导模型.当参数合适时,体系处于拓扑非平庸状态,该拓扑状态由缠绕数Z2描述,此时在纳米线两端涌现两个空间分立的马约拉纳零能模,它受到体系的体态的拓扑性质保护,不受局域的杂质等影响[105].

由于超导体具有粒子-空穴对称性,它的负能级均被填满,而正能级往往是空的,与绝缘体相似,正因如此,绝缘体的拓扑分类理论也能类似地应用到对传统超导体的拓扑分类,该理论指导人们构造和发现了为数众多的拓扑超导体.拓扑超导体近年来得到广泛的研究,一个重要的原因是它能够产生具有非阿贝尔统计的任意子,任意子(anyon)的拓扑保护特性使得它能够运用于抗退相干的拓扑量子计算.根据拓扑物态的体-边对应关系,拓扑非平庸的超导体具有无能隙的元激发,该元激发的色散关系在能带交叉点附近往往是线性的;同时,在布里渊区的一些高对称点上,如Γ,K点等,该元激发能量为零,此时粒子元激发的波函数与空穴元激发的波函数相同:即该零能准粒子的反粒子是其自身,该零能模被称为马约拉纳零能模(Majorana zero mode,MZM),是一种特殊的马约拉纳费米子(Majorana Fermion).在基本粒子物理中,马约拉纳费米子是Dirac 方程的实数解,由意大利物理学家马约拉纳二十世纪三十年代提出,至今仍然没有找到哪种基本粒子是马约拉纳费米子.但是,正如前面所述,在凝聚态物理中,拓扑超导体的元激发有可能具有马约拉纳零能模,它由体系的体态拓扑性质保护,能够抵抗局域微扰,因此能够用于抗退相干的拓扑量子计算[106,107].

目前,实现拓扑超导的主要机制有两种方案:一,自旋三重态配对机制[108];二,自旋轨道耦合[109-111].从实现拓扑超导的材料而言,有本征拓扑超导体和人造超导异质结两种材料,特别地,人造超导异质结为人们构造、探测和操控马约拉纳零模提供了非常好的理论和实验平台,吸引了全世界众多研究小组的注意历和大量投入.2001 年,Kitaev 提出一维无自旋的p 波超导体链能够在两端产生马约拉纳零能模,该马约拉纳零能模受到体态非平庸拓扑保护因而对微弱的局域扰动免疫,该模型在众多文章中均已详尽描述,因此这里就不再赘述.1999 年,Read和Green 提出在px+ipy无自旋二维超导体的涡旋中心能够产生MZM[112],在之后的长时间里,研究人员一直为找到一个具体物理模型实现px+ipy无自旋超导而苦苦寻找而不得,直到2008年傅亮和Kane 才首次提出超导/拓扑绝缘体异质结能够实现该模型[113].紧接着,Sato等[114]甚至提出一个具有强的Rashba 自旋轨道耦合的体系也能等价于px+ipy无自旋超导体模型(见图5),其BdG 哈密顿量如下,

图5 (a),(b),(c)展示了在x 方向为有限边界而y 方向为周期性边界时的能级结构,从(a)到(c)缓慢增加磁场h 的大小,当满足+(0,0)2＜h2＜ψs2 +(0,π)2 时,即(c),边界涌现了两个无能隙的边界模,表明发生了拓扑相变[114]Fig.5.(a),(b),and (c)The band energy of the lattice Hamiltonian with edges at x direction.The magnetic field increases from Figure (a)to Figure (c).The red thin line indicates a gapless chiral edge mode localized on the one side and green thick line a gapless chiral edge mode on the other side.They appear for+(0,0)2＜h2＜ψs2 +(0,π)2 at Figure (c),which indicates the occurrence of topological phase transition[114].

这里,gk2λ(sin(kyd),-sin(kxd))描述Rashba 自旋轨道耦合的强度,σ(σx,σy)是泡利矩阵,h为沿着z轴的塞曼场强度,εk是单粒子的色散关系.Sato 等人观察到上述哈密顿量能够通过一个幺正变换U变换为另一个哈密顿量UHBdG(k)U†,

这里

它等价于s 波和p 波超导配对混合模型,新的s 波“序参量”为-εk和p 波“序参量”dk矢量为gk,因此当gk足够强时,该模型就等价于px+ipy无自旋超导体模型,具体的计算表明:当+ε(0,0)2＜h2＜+ε(0,π)2时,此时拓扑不变量陈数等于1,体边对应关系要求出现两个无能隙的边带模,如下图所示.此时,有一个零能解,满足γ†γ,即马约拉纳零能模.虽然,由于轨道的去配对效应,Sato 等的模型还不能应用到凝聚态物理而更适合应用到超冷原子气体量子模拟等领域.但是,傅亮和Kane、以及Sato 等的工作启发了寻找马约拉纳零能模的一个非常重要的方向,即通过强自旋轨道耦合效应诱导超导体产生自旋三重态配对.

4.3 马约拉纳准粒子的非阿贝尔统计

拓扑物态的体态具有非平庸拓扑性质,在不同拓扑物态的交界处波函数必然出现奇点,该奇点表现为无能隙的边界模,d维拓扑非平庸的体态与(d—1)维边界态之间的这种对应关系被称为体-边对应关系.当超导序参量出现后,由于粒子空穴对称性,无能隙的边界态往往表现为马约拉纳零能模,比如,在二维无自旋p 波超导体的涡旋中心就有马约拉纳零能模,因为涡旋是拓扑超导态与正常态的边界.近年来,前述的一阶拓扑绝缘体概念被推广到高阶拓扑绝缘体,即d维的拓扑非平庸体态拥有(d—n)维的边界态(n＞1).在2016 年到2017 年间,先后有四个小组通过不同的方案提出了高阶拓扑物态的概念,比如,三维拓扑绝缘体拥有一维的或者零维的无能隙边界模[115-118].高阶拓扑绝缘体概念很快被推广到高阶拓扑半金属和高阶拓扑超导体.利用混合超导,如s+id超导配对,便能够在具有Rashba 自旋轨道耦合的铁基超导体/半导体/高温超导体异质结中诱导出高阶拓扑超导体[119];利用高阶拓扑绝缘体/s 波超导体异质结,在无外加磁场情形下便能够实现高阶拓扑超导,形成马约拉纳零能模[120,121].虽然,目前关于高阶拓扑超导体的实验研究还处于初级阶段[122],但是,关于高阶拓扑超导体的理论和实验研究为模拟马约拉纳零能模开辟了新的方向.

由于马约拉纳零能模的存在,拓扑超导体的基态具有2N重简并度(2N为马约拉纳零能模的个数),并且与激发态具有有限大小的能隙.由于费米子(电子)粒子数宇称守恒(Fermion number parity),每一个空间局域的马约拉纳准粒子(马约拉纳准粒子之间相距足够远以至于它们之间完全没有耦合)都能够绝热地被移动,比如绕某一个马约拉纳准粒子绕一圈.该绝热演化将会导致马约拉纳准粒子的世界线(worldline,即时空中的轨迹)在时空中发生缠绕,数学表示为:ψf(T)Ufiψi,Ufi为定义在拓扑超导体的简并基态子空间的幺正矩阵,T为编时算子,为了保证绝热演化,要求操作时间T ≫h/|Δgap|,Ufi也是辫子群B2N的群元,一般地,不同的群元是不对易的,故马约拉纳准粒子满足非阿贝尔统计[106,107,123],下面我们以一维马约拉纳准粒子详细说明.

当交换两对不同的近邻马约拉纳准粒子时,与交换顺序无关,如果|k-l|≥2 时,Bk,k+1Bl,l+1Bl,l+1Bk,k+1;而当两次交换涉及同一个马约拉纳准粒子时,两次交换不对易,详细的代数计算表明:

这就是马约拉纳准粒子的非阿贝尔统计性质.如果相邻的三个马约拉纳准粒子交换三次(|k-l|1),有Yang-Baxter 方程:

方程左右两边的拓扑等价.马约拉纳准粒子的世界线编织受到哈密顿量的拓扑性质保护,因此,任意局域的微弱退相干机制都不能够破坏马约拉纳准粒子,从而实现具有高度鲁棒性的拓扑量子比特,这是拓扑量子比特和拓扑量子计算区别于所有其他量子计算平台的最大不同点和最大优势.一旦实现了可扩展的拓扑超导量子比特,实现相同逻辑量子比特数所需要的物理量子比特数将显著少于其他非拓扑保护的量子计算平台,如半导体量子计算平台.因此,拓扑超导量子计算一直是量子计算领域非常前沿的和具有革命性突破的研究方向.

5 面向量子计算的拓扑超导体在实验上可观测的现象

根据上述对拓扑超导体理论的研究,可以预言一些面向量子计算的拓扑超导体在实验上可观测的现象,通过在实验上探索这些现象又可以反过来表征拓扑超导体.

5.1 马约拉纳零能模和零偏置电导峰 (zerobias conductance peak)

马约拉纳准粒子是拓扑超导体中涌现的非局域准粒子,它的反粒子是其自身.在粒子物理中,马约拉纳准粒子对应于马约拉纳费米子,它由意大利物理学家埃托雷·马约拉纳于1937 年提出.自理论提出之后,科学家们试图在现实材料中寻找到这种准粒子,因为马约拉纳准粒子无论是在基础研究还是应用研究都有深远的意义,它满足非阿贝尔统计,可用来实现容错的拓扑量子计算.2008 年,傅亮和Charles Kane 通过理论计算,预言在拓扑绝缘体和超导体的界面上可能会出现马约拉纳准粒子[113],拓扑超导体由此走入科学家们的视线.由于马约拉纳准粒子的空间非局域性,实验探测变得特别困难,一个间接探测其存在的简易工具是观测其零偏置电导峰.如第4 章所述,在固体材料中,马约拉纳准粒子在拓扑缺陷上的产生湮灭算符满足自共轭关系,这就是马约拉纳零能模,对多个马约拉纳准粒子进行交换编织操作能够形成量子比特.

以一维的拓扑超导纳米线为例,在纳米线的两端各有一个马约拉纳准粒子,它引起的隧穿电导为

其中I是隧穿电流;V是偏置电压;Г是谱的宽度.由此公式可见,在偏置电压为零的时候,有一个电导峰,如果用扫描隧道显微镜 (STM)研究它,会在电子隧道谱上观测到在零能时有个电导峰,即零偏置电导峰,在0 K 温度时,马约拉纳零偏置电导峰的高度为量子化电导值(2e2/h)[124].因此通过实验直接观测马约拉纳零偏置电导峰高度接近2e2/h是证实马约拉纳零模存在的关键证据之一.最近几年多个材料体系在实验上观测到了高度为量子化电导值的零偏置电导峰(详见第6 章节).需要指出的是,对于三维拓扑超导体,在理论上,隧穿极限下的零偏置电导是零[125],在实验上观测到的在零偏置时的电导峰并非真正的零偏置电导峰,往往是由以下一个或几个原因导致[126]: 1)隧穿势垒较低;2)马约拉纳准粒子与正常态存在于表面的狄拉克费米子的能量色散纠缠;3)体材料的超导能隙中有节点或者节线;4)在绝对零度以上,热致宽效应导致零偏置时的凹陷被抹平.

5.2 热导和量子化热霍尔效应 (quantized thermal Hall conductivity)

除了STM 外,输运测量同样可以为马约拉纳准粒子或拓扑超导体的存在提供实验证据.由于在超导态电阻为零,电输运无法用来研究超导态的准粒子,而热输运可以.在超导态时,导电的库珀对无法进行热传导,系统中只有马约拉纳费米子具有热导能力,因此在超导态时测量系统边界的热导就能很好的证实马约拉纳准粒子的存在.

前文中提到,在三维拓扑超导体系统中,无法观测到零偏置电导峰,因此证实三维的拓扑超导体必须要有其他的实验证据.由马约拉纳准粒子的热导出发,科学家们预言在三维拓扑超导体中存在量子化的热霍尔效应[126,127].

科学家们设计出了如图6 所示的材料体系,在三维拓扑超导体的表面覆盖传统s 波超导体.由于近邻效应,三维拓扑超导体表面具有了s 波配对和相位为π 的约瑟夫森结,由此可以在马约拉纳准粒子的狄拉克点处打开能隙.

图6 三维拓扑超导体测量量子热霍尔效应的实验示意图[127]Fig.6.Illustration of the experimental setting for the measurement of quantum thermal Hall effect in the 3D topological superconductor[127].

图6 中红色箭头方向为手性马约拉纳准粒子沿着结的方向扩散产生的量子化热流,它的理论大小为

其中N为三维体材料的拓扑量子数,它和手性马约拉纳准粒子的数量有关,T是趋近于0 K 的温度.从方程(19)可以推算出霍尔热导率为

因此当实验上观测到这样的量子化热霍尔效应同样可以证实在三维拓扑超导体中存在马约拉纳准粒子.目前从这个角度研究拓扑超导体尚不多见.

5.3 反常约瑟夫森效应

不同于常规超导体,拓扑超导体的相位改变既不会破坏对称性,也不会出现临界行为,只会改变相应的拓扑不变量和连续系统的边界特性[128],由此可以设计基于拓扑超导体的约瑟夫森结来观测它的反常约瑟夫森效应.理论上认为,将时间反演不变的拓扑超导体和常规s 波超导体组成约瑟夫森结会出现不同寻常的约瑟夫森效应: 由于配对对称性不同,结上常规的约瑟夫森耦合会非常的弱,但马约拉纳表面态会产生一个非平庸的约瑟夫森耦合[129],这种耦合会出现反常的电流-相位关系[126,129].在拓扑超导体和常规s 波超导体的相位差φ为0 或者π 的时候,受时间反演对称保护,马约拉纳表面态保持无能隙;在相位差φ不为0 或者π的时候,马约拉纳表面态的能隙打开从而降低能量[129].一般约瑟夫森结上电流J和相位差φ之间的关系可以描述为[126,130]

其中Jn和In随着n的增大而减小.由于时间反演对称,J(φ)-J(-φ),因此In0,在此情况下,

考虑到镜像对称,会出现新的约束条件:J(φ)J(π+φ),由此可以推出J2n+1I2n+10 .在这种情况下,J(φ)～sinφ消失了,出现了异常电流-相位关系:

同时,约瑟夫森结的电流-相位关系也可以确定配对势的宇称[130-132].如果配对势的宇称为奇,则系统具有拓扑性;反之,如果配对势的宇称为偶,则系统不具备拓扑性.

因此反常的电流-相位关系可用于确定拓扑超导体的配对对称性,是实验上可以观测到的拓扑超导体的一个重要特征.

5.4 奇频库珀对 (odd-frequency Cooperpairs)

奇频库珀对的概念由Berezinskii[133]于1974 年提出,用于更好的理解非常规超导和超流.在拓扑超导体中,奇频库珀对引发的异常邻近效应导致了基于马约拉纳准粒子的各种奇异现象[134],尤其是零偏置电导峰.

马约拉纳准粒子与奇频库珀对的关系可以通过基于px波超导体的约瑟夫森结的格林函数来分析.当|E|≪Δ(配对势),格林函数可以写作:

马约拉纳准粒子和奇频库珀对通过这个关系式联系起来.(χ*)2f(E;x,x′)的实部是关于E的奇函数,代表了库珀对的奇频对称;(χ*)2f(E;x,x′)虚部是关于E的偶函数,代表了马约拉纳准粒子局域态密度.

根据上述理论分析,以基于纳米线的拓扑超导结构为例,将具有强自旋-轨道耦合的纳米线置于NS 结和SNS 结上(如图7 所示),由于近邻效应,纳米线上有一部分是正常态,一部分是超导态,在纳米线上形成NS 结或者SNS 结.

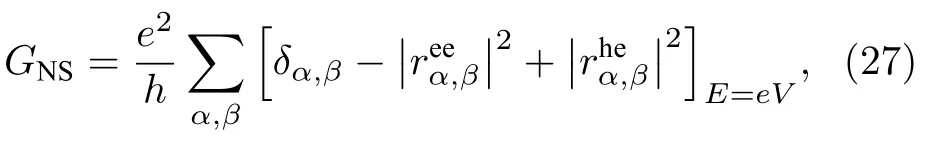
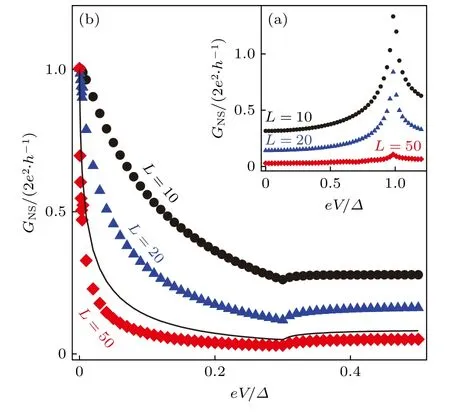
图8 微分电导GNS 随偏置电压eV 的变化曲线 (a)不具有拓扑性的纳米线的曲线[134];(b)具有拓扑性的纳米线的曲线[134]Fig.8.The differential conductance of NS nanowires is plotted as a function of the bias voltage for nontopological nanowire in (a)and for the topological nanowire in (b)[134].

对于SNS 结,具有拓扑性的纳米线在物理机制上和px波超导体一样[134],因此在低温下,拓扑纳米线的SNS 结的约瑟夫森电流表现出了分数的电流-相位关系(如图9 所示):J ∝sin(Δφ/2),其中-π ≤Δφ≤π .

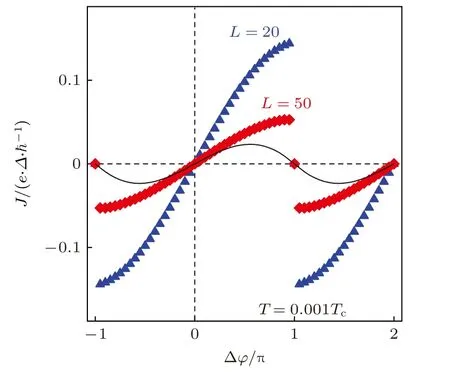
图9 拓扑纳米线的SNS 结的电流-相位关系,作为对比,黑色实线是非拓扑纳米线的电流-相位关系[134]Fig.9.Current-phase relationship in SNS junctions of topological wire.For comparison,the results for nontopological wire is plotted with a solid line[134].

拓扑纳米线的NS 结和SNS 结的异常输运现象都是和奇频库珀对密切相关,由此可见奇频库珀对是实现马约拉纳准粒子不可或缺的,也可以作为表征马约拉纳准粒子的一个重要手段.

6 面向量子计算的拓扑超导体的实验研究进展

目前拓扑超导体的实验研究主要集中在对材料本身的探索上,大体上分为两大类: 本征拓扑超导体和人工构建的拓扑超导体.一些具有非平庸的拓扑能隙函数的超导体、具有奇频库珀对的超导体、以及具有较强自旋三重态特征的非中心对称超导体一般被认为有很大可能是本征拓扑超导体;除此之外,科学家们还将超导体和一些金属、半导体、拓扑绝缘体等材料进行复合,人工构建了一些潜在的拓扑超导体.

6.1 本征拓扑超导体

随着理论和实验的不断推进,越来越多的材料被发现具有本征拓扑超导性.本征拓扑超导体的优势在于可以排除平庸态信号和复杂界面效应的干扰,直接观测到干净的马约拉纳束缚态.

6.1.1 CuxBi2Se3

CuxBi2Se3是最早被发现的拓扑超导材料.2010年,美国普林斯顿大学R.J.Cava 课题组[135]在Bi2Se3中进行Cu 掺杂形成CuxBi2Se3,并在其中发现了Tc=3.8 K 超导性(如图10 所示),从而引发学术界对CuxBi2Se3拓扑超导性的研究.角分辨光电子能谱(ARPES)的研究证实,当Cu 的掺杂量达到超导出现的程度时,CuxBi2Se3在动量空间的拓扑表面态依然存在[136];点接触的电输运方式测量到了CuxBi2Se3的零偏置电导峰[137];用核磁共振测量奈特位移发现CuxBi2Se3在超导态的时候,它的自旋旋转对称性自发破缺,由此可以推论出CuxBi2Se3的超导是由赝自旋三重态的奇频配对引起的,它的自旋角动量被钉扎在某个晶向,因此核磁共振测量给出了CuxBi2Se3是拓扑超导体的直接证据[138];比热的测量也和核磁共振的测量相互印证[139].

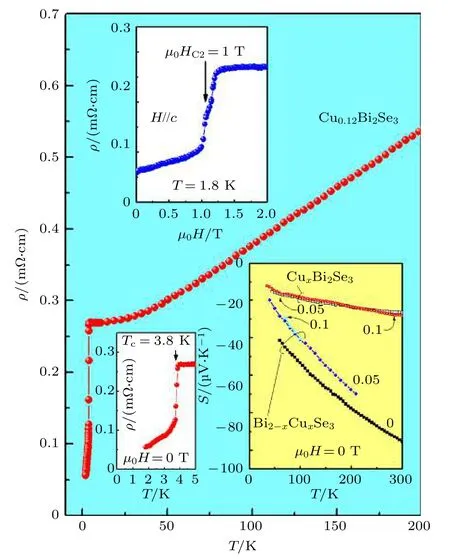
图10 在CuxBi2Se3 中发现了Tc=3.8 K 的超导电性[135]Fig.10.Superconductivity at 3.8 K in CuxBi2Se3[135].

受到CuxBi2Se3晶体的启发,华中科技大学强磁场科学中心的张裕恒、张昌锦课题组利用高温熔融法,将碱土金属元素Sr 替代Cu 插入到拓扑绝缘体Bi2Se3中,获得了高质量的SrxBi2Se3单晶体[140],在10 到35 T 磁场区间SrxBi2Se3出现了周期性的量子振荡信号,证明SrxBi2Se3存在拓扑保护表面态.

Asaba等[141]在Nb 掺杂的Bi2Se3中测量出了超导电性,同时通过磁矩测量还观测到旋转对称性自发破缺,表明在NbxBi2Se3的超导基态具有向列序.

从上述几例中可以看出,对拓扑绝缘体Bi2Se3进行掺杂,掺杂后的材料一旦出现超导,则有望实现本征拓扑超导体.对Bi2Se3掺杂形成的拓扑超导体是目前较为庞大的一个拓扑超导体系,也是研究较为全面和深入的材料体系.

6.1.2 Fe1+ySexTe1-x

Fe1+ySexTe1—x是典型的铁基非常规超导体,中国科学院物理研究所的丁洪研究员团队和高鸿钧院士团队对Fe1+ySexTe1—x的拓扑性质进行了系统的谱学实验研究.要证实Fe1+ySexTe1—x的本征拓扑性需要在谱学上观测到三个现象[142]: 1)狄拉克锥表面态;2)表面态处有螺旋自旋极化,使得自旋方向垂直于动量方向;3)在超导态时,表面态有s波超导能隙.

2014 年,丁洪课题组[143]在尝试调控Fe1+ySexTe1—x费米能级的时候发现了狄拉克锥表面态的初步迹象[144],理论计算表明这一能带反转具有拓扑非平庸的性质,即使Fe1+ySexTe1—x单晶薄至单层依然可以通过ARPES 观测到拓扑非平庸能带反转[145,146];2018 年,该课题组利用超高分辨ARPES证实了Fe1+ySexTe1—x在费米能级处有狄拉克锥式的自旋螺旋表面态,且在超导态展现出s 波超导能隙[142];同年,利用He-3 极低温强磁场STM 系统对Fe1+ySexTe1—x的测量验证了它的狄拉克锥拓扑表面态,并在磁通涡旋处观察到尖锐的零偏置电导峰,这也是首次清晰的观测到了纯净的马约拉纳束缚态[147],它的零偏置电导峰在低温下表现出量子化的电导,即可以观测到马约拉纳零能模的近量子化电导平台特征(如图11 所示),以往导致平台电导值小于量子化电导2e2/h的因素可能和系统能量展宽和准粒子中毒效应有关[148];进一步的STM研究表明,有两类超导涡旋共存于Fe1+ySexTe1—x表面: 拓扑涡旋和平庸涡旋,马约拉纳零能模存在于拓扑涡旋中,同时伴有整数量子化能级序列的涡旋束缚态(En=nΔ2/EF,n=0,±1,±2,··· 其中n=0是马约拉纳零能模),而平庸涡旋中没有马约拉纳零能模,且其涡旋束缚态能级序列呈现半整数行为(En=nΔ2/EF,n=±1/2,±3/2,±5/2,···)[149].

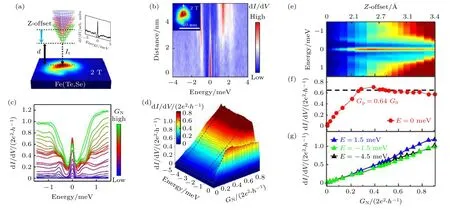
图11 Fe1+ySexTe1—x 上马约拉纳零能模的近量子化电导平台特征 (a)扫描隧道显微镜示意图[148];(b)小图中涡旋的线界面图[148];(c)微分电导谱[148];(d)三维微分电导谱[148];(e)图(c)的彩色图[148];(f),图(e)在零偏置是的水平切线[148];(g)图(e)在高偏置是的水平切线[148]Fig.11.Zero-bias conductance plateau observed on Fe1+ySexTe1—x: (a)Schematic of variable tunnel coupling STM/S method[148];(b)a line-cut intensity plot along the dashed white arrow in the inset[148];(c)an overlapping plot of dI/dV spectra[148];(d)3D plot of tunnel coupling dependent measurement,dI/dV (E,GN)[148];(e)color-scale plot of Figure (c)[148];(f)horizontal line-cut at the zero-bias from Figure (e)[148];(g)horizaontal line-cuts at high-bias from Figure (e)[148].

除了谱学研究,Fe1+ySexTe1—x的电磁学研究为其拓扑性提供了一些佐证.在对过量铁的Fe1+ySexTe1—x薄片的电磁输运和扫描超导量子干涉仪(sSQUID)的研究中发现,虽然铁杂质的存在大大压制了块材的超导性,材料的边缘却显现出稳固的超导性(如图12 所示),这种在热与磁性干扰下保持稳固的本征性质暗示这一边缘超导很可能有拓扑性的根源[150].

图12 超导抗磁性在Fe1+ySexTe1—x 薄片中的分布 (a)样品光学显微镜照片[150];(b),(c)样品的抗磁和磁化强度sSQUID 扫描图[150];(d)—(g)随温度变化的抗磁sSQUID 扫描图[150];(h)图(d)中r 箭头指向的不同温度抗磁曲线[150];(i)根据图(h)做出的彩图[150];(j)在图(d)中1和2 两点处提取的随温度变化的超流密度[150]Fig.12.Distinctive edge features in susceptometry of Fe1+ySexTe1—x flake: (a)Optical image of the sample[150];(b),(c)the susceptometry and magnetometry images of the sample,respectively[150];(d)—(g)susceptometry images of the sample at various T[150];(h)line cuts of the susceptometry images at various T along the vector direction (r)as labeled by the arrow in Figure (d)[150];(i)interpolated image from the line cuts in Figure (h)[150];(j)superfluid densities as a function of T extracted from point 1 and 2 in Figure (d)[151].

Fe1+ySexTe1—x是目前研究得较为深入和全面的拓扑超导体,具有向qubit 原型器件进一步推进的可能.

6.1.3 Li(Fe,Co)As

Li(Fe,Co)As是铁基超导体中又一个可能存在拓扑超导性质的材料.在LiFeAs 的能带结构测量中并没有发现其具有拓扑性,但当利用高分辨的激光ARPES和具有自旋分辨的ARPES 对Co 掺杂的LiFeAs 进行能带结构研究时,发现Li(Fe,Co)As 具有拓扑非平庸性的能带反转(如图13 所示),确认了在费米能级附近同时具有拓扑绝缘态和狄拉克半金属态,通过改变载流子的掺杂可以将拓扑非平庸能带调控到费米能级,从而可以在同一个材料中得到多个不同的拓扑超导态[152].

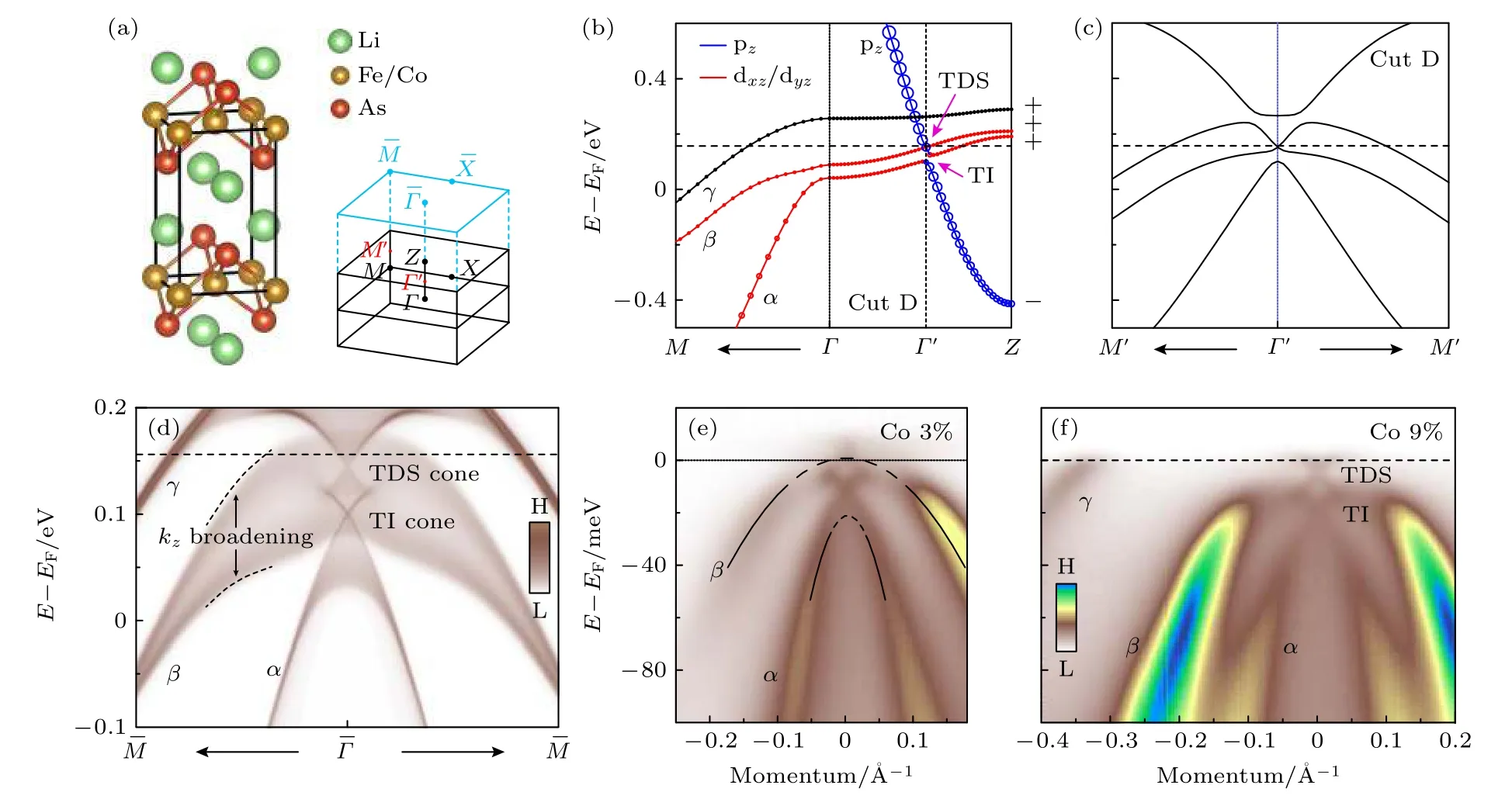
图13 Li(Fe,Co)As 的电子结构 (a)Li(Fe,Co)As 的晶体结构[151];(b)LiFeAs随ΓM和ΓZ 的能带色散[151];(c),(b)Cut D 处的面内能带结构[151];(d)LiFeAs (001)面的表面谱[151];(e)15 K 时LiFe1—xCoxAs (x=3%)的ARPES谱[151];(f)10 K 时LiFe1—xCoxAs(x=9%)的ARPES谱[151]Fig.13.Electronic structure of Li(Fe,Co)As: (a)Crystal structure of Li(Fe,Co)As[151];(b)zoomed-in view of the LiFeAs band dispersion along ΓM and ΓZ[151];(c)in-plane band structure at Cut D in Figure(b)[151];(d)(001)surface spectrum of LiFeAs[151];(e)ARPES intensity plot of LiFe1—xCoxAs (x=3%)at 15 K[151];(f)ARPES intensity plot of LiFe1—xCoxAs (x=9%)at 10 K[151].

6.1.4 (Li,Fe)OHFeSe

(Li,Fe)OHFeSe 同样也是铁基超导体中具有拓扑超导性质的一种材料,它的Tc高达42 K.中国科学技术大学的封东来院士课题组[152]对该材料进行了系统的研究.首先在ARPES 的测量中观测到了狄拉克锥表面态,能带计算也确认其拓扑性质;在无缺陷的(Li,Fe)OHFeSe 样品区域用STM发现了涡旋处的零偏置电导峰[152];通过使用极高能量分辨率的STM 对(Li,Fe)OHFeSe 进一步的研究,发现了马约拉纳零能模诱导的共振Andreev反射现象及量子化的零偏置电导峰[153](如图14 所示);具有高空间分辨的低温STM 测量发现非零能态展现出清晰的空间振荡,而零能模则没有发现振荡[154],这一发现与理论上(Li,Fe)OHFeSe 体材料的s++波配对和表面的拓扑超导态相一致.

图14 (Li,Fe)OHFeSe 中量子化的零偏置电导峰[153]Fig.14.Quantized zero-bias conductance peak in (Li,Fe)OHFeSe[153].

6.1.5 Sn1—xInxTe

SnTe和Bi2Se3类似,也是一种拓扑绝缘体,对其中2%或以上的Sn 进行In 替换会使其成为超导体[155].在不同掺杂量的Sn1—xInxTe 晶体中,当x≈ 0.04 (Tc≈ 1.2 K)时,零偏置电导峰也能被观测到[156](如图15 所示),同时,ARPES 的测量表明In 掺杂后拓扑表面态保持完整[157],Sn1—xInxTe的拓扑超导性得到进一步验证.需要指出的是,目前只在x≈ 0.04 组分中看到了零偏置电导峰.

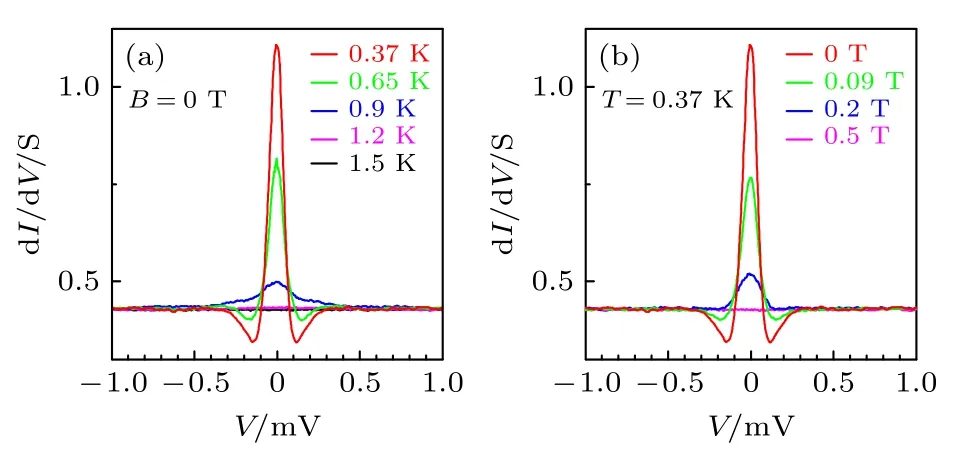
图15 Sn1—xInxTe 的零偏置电导峰 (a)固定磁场改变温度[156];(b)固定温度改变磁场[156]Fig.15.Zero-bias conductance peak in Sn1—xInxTe: (a)Different temperatures at B=0 T[156];(b)different magnetic fields at T=0.37 K[156].

6.1.6 TaSe3

2018 年有理论学家通过第一性原理计算预言TaSe3有可能是拓扑超导体[158],从而引起了学术界的广泛关注.科学家们利用ARPES,STM、电输运测量等实验手段对这一新型准一维超导材料TaSe3的电子结构进行了系统的研究,成功观测到该材料的拓扑表面态(如图16 所示),从而确认了该材料的拓扑属性,并通过STM 测得了它的超导能隙约为0.25 meV,证明了TaSe3是潜在的拓扑超导材料[159,160];在台阶式的边缘附近还观测到更多的边界态,这很可能有拓扑性的根源[160].

图16 TaSe3 的电子结构[159]Fig.16.Electronic structure of TaSe3[159].

6.1.7 2M-WS2

WS2作为过渡金属硫族化合物(TMDCs)中的一员,是二维材料领域研究的热点之一.以往对WS2的研究主要集中在1T’相,因为该相的制备工艺比较成熟.2019 年中国科学院上海硅酸盐研究所的黄富强团队通过拓扑化学的方法成功制备出2M相的WS2单晶,该单晶表现出8.8 K 的超导转变温度,是本征TMDCs 材料中最高的,理论计算表明该材料的能带中存在受拓扑保护的狄拉克锥拓扑表面态[161](如图17 所示);之后科学家们利用低温强磁场STM 观测2M-WS2磁通内态密度随空间的演化,发现了空间各向异性的马约拉纳束缚态,这可能是各向异性的超导序参量和拓扑表面态共同导致的[162],进一步证实2M-WS2是拓扑超导体.

图17 2M-WS2 的拓扑表面态 [161]Fig.17.Topological surface states of 2M-WS2[161].

6.1.8 PbTaSe2

在非中心对称的材料中,由于反转对称性破缺,可以使得s 波和p 波并存,如果p 波的能隙大于s 波的能隙,那么这个超导体就是拓扑的[163].PbTaSe2是非中心对称的TMDC 材料,有很强的自旋-轨道耦合,同时还具有转变温度为1.8 K 的超导电性,有理论计算表明PbTaSe2有拓扑的能带结构[164].ARPES 的研究发现PbTaSe2拥有拓扑节线态,是整数拓扑不变量,被反射对称保护[165];利用准粒子散射干涉成像可以观测到PbTaSe2中有两个拓扑表面态(如图18 所示),内部拓扑表面态在费米能级处与附近的体态完全分离,而外部拓扑表面态在费米能级处融入附近的体态[166];研究人员还在PbTaSe2观测到点接触谱中具有一直持续到表面超导上临界场的二重对称性,暗示其可能是一种“仅存在于表面”的向列性超导[167].

图18 PbTaSe2 中有两个拓扑表面态[165]Fig.18.Two topological surface states in PbTaSe2[165].

6.1.9 β-Bi2Pd

除了上述非中心对称超导体具有成为拓扑超导体的可能性,中心对称的超导体同样也会有机会成为拓扑超导体,比如β-Bi2Pd.自旋分辨ARPES观测到了β-Bi2Pd 正常态费米能级处有拓扑表面态[168];尽管β-Bi2Pd 单晶并未在实验上观测到零能束缚态,但是在分子束外延制备的β-Bi2Pd 薄膜中可以用ARPES 观测到拓扑表面态在低温下打开一个受时间反演对称性保护的超导能隙,该超导能隙大于体态的超导能隙,同时,在磁通涡旋中心附近观察到了马约拉纳零能模引发的零偏置电导峰[169,170](如图19 所示),这些都为确认β-Bi2Pd是拓扑超导体提供了实验上的证据.

图19 分子束外延β-Bi2Pd 薄膜的拓扑超导电性和马约拉纳零能模 (a)扫描隧道显微镜的扫描图[169];(b)β-Bi2Pd 的微分电导谱[169];(c)归一化的零偏置电导峰分布图[169];(d)隧穿电导谱[169];(e)涡旋核心附近的归一化微分电导谱[169]Fig.19.Topological superconductivity and MZM in β-Bi2Pd film grown by MBE: (a)STM topography[169];(b)Differential conductance dI/dV spectrum[169];(c)normalized zero-bias conductance map[169];(d)tunneling conductance dI/dV spectrum[169];(e)normalized dI/dV spectra measured at location with radial distance r from the vortex center[169].

6.1.10 WTe2

WTe2晶体是“第二类外尔半金属”,具有拓扑不闭合表面态、量子自旋霍尔效应[171]、巨磁阻[172]等特性.由于其是层状材料,易于解理,当解理到单个晶胞厚度时,WTe2由外尔半金属态变成了二维拓扑绝缘体态,并在实验上观测到了一维导电边界态[173],证实单个晶胞厚的WTe2是拓扑非平庸体系.在此基础上,科学家们对此体系进行门电压调控载流子浓度,获得了超导电性[174,175](如图20所示),并且发现边界态也是超导的.

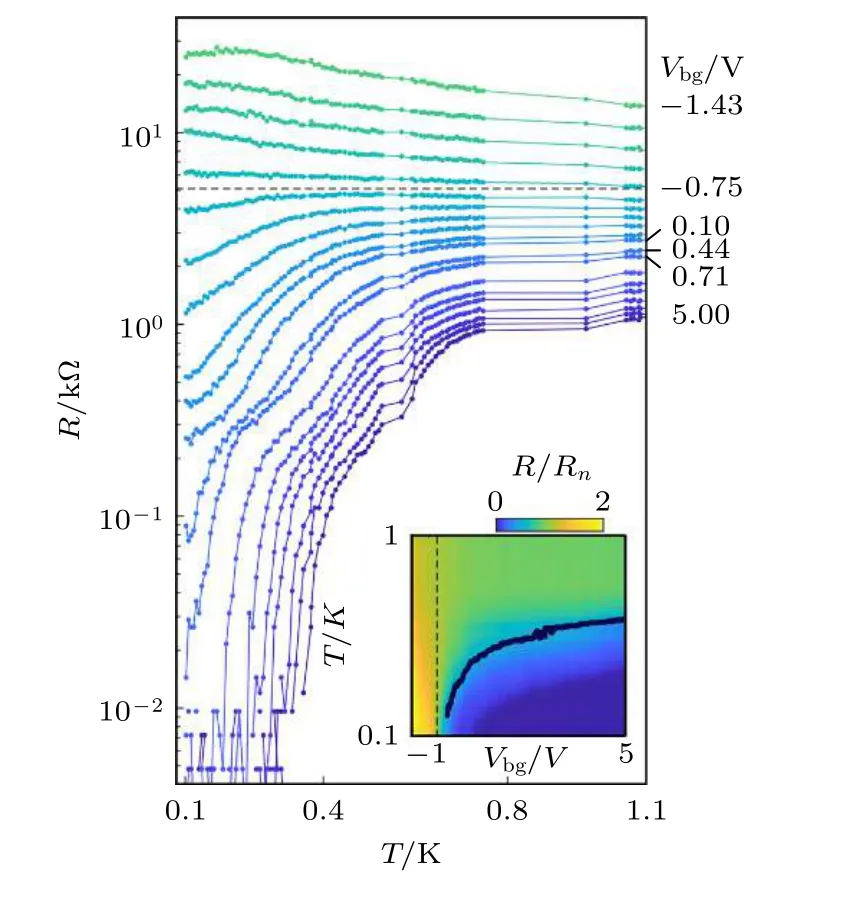
图20 单个晶胞厚的WTe2 通过门电压调控出超导电性[174]Fig.20.Gate-tuned superconductivity in monolayer WTe2[174].

除了对单个晶胞厚的WTe2进行电场调控产生超导外,科学家们还通过对WTe2晶体进行加压[176,177]和K 掺杂[178]等手段获得了超导电性.种种迹象表明,WTe2中可能存在马约拉纳零能模.

在上述的多个拓扑超导材料体系中,如Li(Fe,Co)As,(Li,Fe)OHFeSe,PbTaSe2和β-Bi2Pd 等,目前仅有谱学研究的实验证据,尚缺少输运方面的实验研究,后期的研究工作重点可以放在输运研究,以取得更多的实验证据.

6.2 人工构建的拓扑超导体

人工构建的拓扑超导体主要是由两部分组成:自旋非简并金属和s 波超导电性.2008 年,傅亮和Kane[113]最早在理论上提出了人工构建拓扑超导体的可行性,他们设想将s 波超导体和具有拓扑表面态的拓扑绝缘体堆垛在一起,就会得到一个等效的二维p 波超导体,在涡旋处会出现马约拉纳零能模.

6.2.1 拓扑绝缘体/s 波超导体异质结

2012 年,上海交通大学贾金锋院士课题组[179]在NbSe2单晶表面通过分子束外延方式生长出原子级清晰的拓扑绝缘体Bi2Se3,这种异质结构中的s 波超导体NbSe2通过邻近效应将超导电性注入到拓扑绝缘体Bi2Se3中,ARPES和STM 的测量证实Bi2Se3的表面具有超导能隙,成功实现了超导态和拓扑态的共存;2014 年,该课题组成功生长出质量更好的拓扑超导异质结构Bi2Te3/NbSe2,通过极低温强磁场STM 在拓扑绝缘体Bi2Te3的表面观测到Abrikosov 涡旋和Andreev 低能束缚态,表明Bi2Te3薄膜表面的超导是拓扑超导[180];对Bi2Te3表面量子磁通涡旋处的束缚态空间分布进行系统研究,发现当Bi2Te3大于三层后,拓扑表面态形成,Bi2Te3上零偏置电导峰在远离涡旋中心20 nm 处劈裂(如图21 所示),这种行为可能源自马约拉纳零能模,为进一步实现对马约拉纳准粒子的调控奠定了基础[181].

图21 Bi2Te3/NbSe2 上的零偏置电导峰劈裂 (a)电导曲线[181];(b)通过图(a)做出的彩色图[181];(c)—(g)2—6 层的电导彩色图[181];(h)劈裂点随层数变化曲线[181]Fig.21.(a)A series of dI/dV curves[181];(b)the color image of Figure (a)[181];(c)—(g)the experimental results for 2-6QL samples,following the similar data process of Figure (b)[181];(h)summary of the start points of the peak split [181].

该材料体系非常适合用来研究马约拉纳费米子的新奇特性.

6.2.2 半导体-超导体异质纳米线

半导体-超导体异质纳米线因其制备门槛低并可用门电压调控,成为拓扑超导体研究的热点材料体系.理论上预言将强自旋-轨道耦合的半导体纳米线与s 波超导体进行耦合,在外加磁场的作用下,可以在纳米线两端出现马约拉纳准粒子[182,183].该材料体系要求半导体纳米线具有较强的自旋-轨道耦合、较大的朗道g因子、较高的迁移率且与超导体容易耦合.科学家们先后在超导体NbTiN 与InSb 纳米线的耦合系统(NbTiN/InSb)[184]、超导体Nb 与InSb 纳米线的耦合系统(Nb/InSb)[185]、超导体Al 与InAs 纳米线的耦合系统(Al/InAs)[186]中观测到了零偏置电导峰.由于早期工艺原因,器件的杂质和缺陷较多,无法观测到量子化的零偏置电导峰.分子束外延技术的引入,使得器件质量大幅度提高,纯净能隙中的零偏置电导峰能被观察到[187,188](如图22 所示).

图22 分子束外延生长的Al/InAs 结构中测得的量子化零偏置电导峰 (a)B-Vsd 扫描谱[187];(b)从图(a)中提取的不同磁场下的微分电导曲线[187]Fig.22.Quantum zero-bias conductance peak in Al/InAs grown by MBE: (a)B-Vsd sweep[187];(b)differential conductance line-cut plots taken from Figure (a)at various B values[187].

由于半导体-超导体异质纳米线的材料和器件制备与目前的半导体工艺相兼容,成为了拓扑超导体的主流研究方向之一,也是研究推进得最快的方向之一,是最有可能实现实际应用的材料体系.

6.2.3 量子阱与超导薄膜耦合形成约瑟夫森结

2017 年有理论指出将具有强自旋-轨道耦合的二维电子气置于两层超导铝电极之间,形成面内约瑟夫森结可以实现拓扑超导电性[189].2019 年,有科学家根据这个设想设计出一种约瑟夫森结,它是HgTe 量子阱与薄膜Al 耦合形成的.可以通过控制结上的相位差和改变面内磁场的大小来实现从传统超导态到拓扑超导态的转变[190],通过测量结边缘的隧穿谱来确定拓扑超导态: 在弱磁场下,整个器件处于常规超导状态,并未观测到零偏置电导峰;随着磁场的增加,在一定相位差范围内观测到了零偏置电导峰,意味着此时整个器件进入了拓扑超导态(如图23 所示),这些研究结果和之前的理论计算结果保持一致.

图23 不同磁场下隧穿电导峰[190]Fig.23.The differential conductance curves as a function of the bias voltage at different magnetic fields[190].

7 拓扑超导体用于量子计算的展望

基于传统超导体、半导体或者光学的量子计算机已经显示出远强于普通计算机的计算能力[95-97],实现了“量子优越性”.然而它们各自都有一些缺陷,尤其是在相干时间上,退相干是无法避免的,因此制备稳定的量子比特模块是量子计算发展过程中必须要去面对和解决的问题,基于拓扑超导的拓扑量子计算便是能够克服这个难题的技术路线之一.

目前已经证实多个材料体系具有拓扑超导电性,其中半导体-超导体异质纳米线最为接近实际应用,因为其在材料制备和器件加工方面与现有的技术相兼容,工艺相对成熟,并已经有明确可行的理论路线图来实现非阿贝尔任意子编织和拓扑量子计算[191],是国际上的一个主流方向,对于这个材料体系,下一步除了深入理解马约拉纳费米子更多的物理特性外,还需大力推进器件和系统设计,最终构建稳定的量子比特模块,实现量子计算.

拓扑绝缘体/s 波超导体异质结体系是研究多个马约拉纳零能模相互作用的理想平台,对这类体系可以使用电场调控拓扑超导涡旋从而实现拓扑编织.因此,对于此类材料体系,一方面需要研究马约拉纳准粒子的新奇特性,另一方面要将研究推进到马约拉纳零能模的调控、编织等方面,为制备稳定的量子比特做好技术上的储备.

本征拓扑超导体,尤其是拓扑非平庸的铁基超导材料,是能在单一材料中实现纯净马约拉纳零能模的理想材料.对该材料体系中马约拉纳涡旋态宏观调控已经有一定的实验积累,下一步将会探索在实验上观测非阿贝尔统计,实现拓扑量子计算.

在理论和实验方面,拓扑超导体在量子计算中取得了一系列重要的进展和成果,相比于其他量子计算技术路线,由于材料受拓扑保护,基于拓扑超导体的量子计算有望解决量子比特退相干与容错量子计算的关键问题;但利用拓扑超导体完全实现量子计算还面临巨大挑战,尚未在实验上直接验证非阿贝尔统计,目前该领域正处于研究的关键阶段,围绕二维拓扑超导体的探索可能为马约拉纳零能模的探测与编织提供更优平台,有望在不远的将来实现质的飞跃.