Self-similarity of spanwise rotational motions’ population trends in decelerating open-channel flow
2022-08-26PngZhngYnhongDunQingZhongDnxunLiShngfYngJingHuWnjiLi
Png Zhng , Ynhong Dun , Qing Zhong , ,, Dnxun Li , Shngf Yng , Jing Hu ,Wnji Li
a National Engineering Research Center for Inland Waterway Regulation, Chongqing Jiaotong University, Chongqing 40 0 074, China
b State Key Laboratory of Hydroscience and Engineering, Tsinghua University, Beijing 10 0 084, China
c College of Water Resources & Civil Engineering, China Agricultural University, Beijing 10 0 083, China
d Beijing Engineering Research Center of Safety and Energy Saving Technology for Water Supply Network System in China Agricultural University,Beijing 10 0 083, China
e Key Laboratory of Ministry of Education for Hydraulic and Water Transport Engineering, Chongqing Jiaotong University, Chongqing 40 0 074, China
Keywords:Self-similarity Population trends Spanwise rotational motions Decelerating open-channel flow Equilibrium flow
ABSTRACT Decelerating open-channel flow is a type of flow that gradually moves forward with decreasing velocity and increasing water depth. Although all flow parameters change along the streamwise direction,previous studies have revealed that these parameters’ vertical distributions at different sections can be universally described with a single profile when being nondimensionalised by appropriate scales. This study focuses on the population trends of spanwise rotational motions at various sections along the main flow direction by particle imaging velocimetry (PIV) measurement. The wall-normal population distributions of density, radius, swirling strength, and convection velocity of the prograde and retrograde motions show similar trends in uniform open-channel flows. The dimensionless representation is invariant along the main flow direction. This study’s results indicate the self-similar characteristic of population trends of spanwise rotational motions prevails in decelerating open-channel flow.
Decelerating open-channel flows are commonly encountered in natural streams and engineering canals [1–4] . For example, a reservoir provides a typical decelerating open-channel flow in the backwater region ( Fig. 1 ). Due to the dam’s blocking, the flow gradually moves forward with decreasing velocity and increasing water depth along the main flow direction. Compared with uniform flows, decelerating flows exhibit more complicated flow structure and sediment transport characteristics due to rising water depth and reducing surface slope, averaged section velocity, and averaged bed shear stress along the streamwise direction [5–7] .
Despite their complexity, most decelerating open-channel flows can be considered in equilibrium flow conditions, i.e., there exists a unique profile invariant along the main flow direction [ 5 , 8 ].Previous studies have revealed that decelerating equilibrium flows maintain self-similar mean flow characteristics at different sections along the main flow direction irrespective of flow parameters, e.g.,flow velocity and water depth [8–11] . As shown by Kironoto and Graf [10] and Song and Chiew [8] , the vertical distributions of mean velocity, turbulence intensity, and Reynolds stress in various sections along the main flow direction can be universally described by a single profile when being non dimensionalised by appropriate scales (such as cross-sectional mean velocity, maximum velocity in the profile or bed-shear stress). The self-similarity characteristics of Reynolds shear stress and turbulence intensities were also confirmed by Yang and Chow [12] in their experimental results. Recently, Pu et al. [13] proposed exponential equations for turbulence intensities and Reynolds stress with the equilibrium pressure gradient parameter.
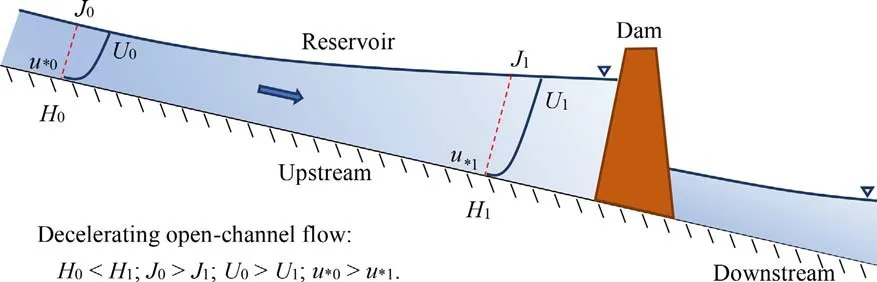
Fig. 1. Sketch of decelerating open-channel flow upstream of a reservoir ( J, H, U , and u * represent water surface slope, water depth, depth-averaged velocity, and friction velocity, respectively).
While the self-similar distributions of mean velocity, turbulence intensity, and Reynolds stress have been confirmed, a natural question arises of whether the coherent structures in different sections along the main flow direction in the decelerating open-channel flow exhibit similar self-similarities. It is generally known that different types of coherent structures play essential roles in determining mean flow, stress, and other statistical properties in other uniform wall-bounded turbulence [14–17] . The spanwise rotational motions, which rotate around the spanwise direction, are typical coherent structures that attract great concern [18–20] . The inherent momentum transportation role of these spanwise rotational motions can give rise to ejection (the fluctuating streamwise velocityu′<0 and wall-normal velocityv′>0, called Q2 event) and sweep events (u′>0 andv′<0, called Q4 event), which have been demonstrated to carry a large amount of turbulent kinetic energy and Reynolds stress [ 17 , 21 ], and therefore indicate the vital contributions of these spanwise rotational motions to the turbulence statistics [22] .
The population characteristics of spanwise rotational motions(e.g., core size, orientation, density, and convection velocity) have been extensively studied in boundary layer [ 23 , 24 ], closed channel[ 25 , 26 ], and (uniform) open-channel flows [27] . However, they are still to be quantified in decelerating open-channel flows. Furthermore, it remains unclear whether these spanwise rotational motions’ population trends in decelerating open-channel flows exhibit similar self-similar characteristics along the main flow direction as the documented self-similarities for the mean flow quantities.The present research provides experimental evidence for the selfsimilar population trends of spanwise rotational motions in decelerating open-channel flow by particle imaging velocimetry (PIV)experiments.
The experiments were performed in a recirculating openchannel flume with dimensions of 28 m long, 0.56 m wide, and 0.7 m deep. The flume has glass beds and sidewalls, allowing flexible arrangements for PIV measurement. Three 5 × 5 cm grids at the flume entrance removed possible large-scale flow structures and facilitated quick flow development. An electromagnetic flowmeter and seven ultrasonic level sensors monitor the flow and water depth along the flume. The streamwise and wall-normal directions are denoted byxandy, respectively. Details of the flume and its characteristics can be found in Zhang et al. [28] .
Instantaneous velocity fields were measured using a homemade PIV system in thex–yplanes. The flow was seeded with hollow glass particles, with a mean diameter of 10 μm and a density of 1.03 g/cm3. A continuous-wave laser (10 W) with a Powell lens produced a 1 mm-thick light sheet for illumination. The experiment used a 2560 × 1920 pixels CMOS camera configured with a Nikon 50 mm f/1.8 D lens for image acquisition. Particle images were analysed using the iterative multigrid image deformation method [29] . Test results of the PIV algorithm can be found in a report of the 4th International PIV Challenge (under the symbol TsU, Kähler et al. [30] ).
Figure 2 shows the experimental steady decelerating openchannel flow with a bed slope of 2.5 mm per meter, which maintains uniform flow conditions in the near-entrance region with a water depth of 30 mm and transits to gradually varied flow at about 12 m from the entrance. Measurements were carried out at four test sections, i.e., S1, S2, S3, and S4, along the streamwise direction, with 9 m, 17 m, 20 m, and 25 m from the entrance, respectively. The flow remains steady during the whole experiment.The details of the test flow condition are listed in Table 1 .
The sampling frequency was set to 1 Hz to ensure statistical independence between successive flow fields to analyse the population trends of the prograde/retrograde motions. Frame exposure time was fixed at 400 μs to compromise between minimising image streaking and maximising image brightness. The time interval between the two frames in an image pair was adequately determined to be 1.25 ms. The parameters of PIV interrogation are listed in Table 2 . The PIV final interrogation window size of the four sections is different. Due to the friction velocity of decelerating open-channel flow changes along the main flow direction, the consistency of inner-scaled vector spacing in the streamwise (or wall-normal) direction at four sections can be ensured by using different sizes of the final interrogation window. The background subtraction, windows deformation, and vector validation algorithm of the PIV system can be found in Zhang et al. [28] .
Analysing spanwise rotational motions’ characteristics necessitates identifying and extracting rotational motions from instantaneous velocity fields. A popular rotational motion identification method involves swirling strength,λci, the imaginary part of the local velocity-gradient tensor’s complex eigenvalue, as a valid rotational motion indicator [31] . The instantaneous fluctuating spanwise vorticity (ωz) is commonly used to indicate the rotation sense of a spanwise rotational motion [ 19 , 25 , 32 , 33 ]:

whereΛci<0 represents a prograde motion with clockwise rotation, andΛci>0 illustrates a retrograde one with counterclockwise rotation.
To simplify the determination of a universal threshold, Wu and Christensen [25] recommended normalisingΛciwith its root-mean-square to eliminate its wall-normal non-uniformity. As shown by Chen et al. [27] , an improvement could be further made by separate accounting for prograde and retrograde motions as follows:

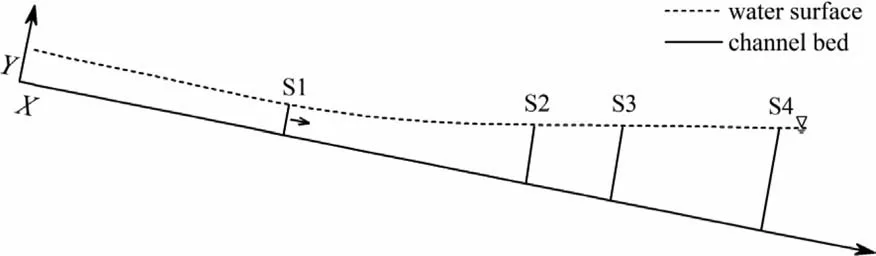
Fig. 2. Sketch of flow direction profile ( X denotes the distance from flume entrance).

Table 1 Flow Conditions. a

Table 2 PIV interrogation parameters. a
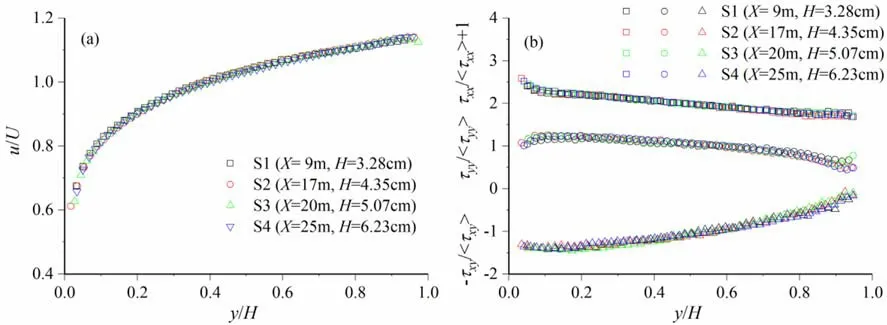
Fig. 4. Velocity profiles are normalised by the local depth-averaged velocity ( a ), normalised turbulence intensities, and Reynolds stress profiles ( b ).
Figure 3 shows a realisation of the identified rotational motions in an instantaneous velocity field with the procedures proposed by Chen et al. [27] . The red and blue colour-filled contours represent retrograde and prograde motions, respectively. Localised Galilean decomposition (taking the streamwise velocity at the centre of the rotational motion as convection velocity) was used to visualise these rotational motions (see black (prograde motions) and orange (retrograde motions) vectors in Fig. 3 b–e). This local decomposition confirms that all regions of non-zeroΛciare indeed associated with closed streamline patterns, as mentioned in Wu and Christensen [25] .
Verifying the equilibrium condition in the current decelerating open-channel flow was done by plotting the velocity profiles,u/U(Uis the depth-averaged velocity), againsty/H, as shown in Fig. 4 (a). Moreover, Fig. 4 b shows the wall-normal distributions of Reynolds normal stress (τxxorτyy) and Reynolds shear stress (τxy)normalised by each depth-averaged value (<>represent depthaveraged of the wall-normal distribution profiles). The present research provides experimental evidence for the self-similar population trends of density, radii, swirling strength, and convection velocity of spanwise rotational motions in decelerating open-channel flow. The depth-averaged value has perfect statistical stability and convergence for the dimensionless parameters of different characteristics.
It can be seen that the self-similarity characteristic is evident in equilibrium along the entire measured sections despite some insignificant deviations in the near-surface region of velocity profiles( Fig. 4 a) and Reynolds stress profiles ( Fig. 4 b). The value ofu*/Umaxat each section remains constant at 0.04, in agreement with the results by Kironoto and Graf [10] , which further supports that the experimental flow is in equilibrium condition.
Following Wu and Christensen [25] , the population density of prograde (retrograde) rotational motions,Πp(r)(y), is defined as the ensemble-averaged number of prograde (retrograde) spanwise rotational motions,Np(r)(y), whose centres reside inΔy×Lx(streamwise field of view) rectangle centred aty:

To investigate the self-similar trends, the population density,Πp(r)(y), is further normalised by the local depth-averaged value,<Np(r) (y)>.
Figure 5 shows the normalised population densities of prograde and retrograde rotational motions in decelerating open-channel flow. The profiles at different sections overlap, which is a strong manifestation of similar tends to vary sections along the main flow direction. Moreover, the results of uniform open-channel flow,closed channel flow, and turbulent boundary layer are also included for comparison (see closed symbols in Fig. 5 ). Figure 5 a shows that the vertical population trends of prograde rotations under different flow conditions are similar, gradually decreasing with increasingy/H. The vertical distribution characteristics of prograde and retrograde rotations in the decelerating open-channel flow are some similarities to those in the uniform open-channel flow but different from that in closed channel flow and turbulent boundary layer (as shown in Fig. 5 b), which can be plausibly attributed to the potential free surface effect in open-channel flows.
As shown in Fig. 3 , a spanwise rotational motion can be circular, elliptical, or irregular. Its core area,A, is determined using the region-growing algorithm proposed by Gao et al. [26] . According to the method, a single vortex structure with only one peak point can be obtained. Therefore, the area of the vortex structure is a product of several points in the vortex region and a quarter of the area of the PIV final interrogation window. Based on averaging over prograde and retrograde motions, respectively, the equivalent radius is calculated as follows,

For illustrating the self-similarity,Rp(r)(y) is also normalised with the local depth-averaged value,<Rp(r)(y)>. Figure 6 shows the normalised radii of prograde and retrograde rotational motions in decelerating open-channel flow, respectively.
Again, similar characteristic prevails in different sections as the profiles overlap. There exists a very slight decreasing trend in Fig. 6 a (prograde motions) and 6 b (retrograde motions). These wall-normal trends indicate that the population radii of prograde and retrograde rotational motions are insensitive toy/H. Moreover,the results of uniform open-channel flow from Chen et al. [27] are also included for comparison. The normalised radii of prograde and retrograde rotational motions in decelerating open-channel flow are more homogenised along the depth direction than those in the uniform open-channel flow.
Rotational motion strength,Λp(r)(y), is calculated based on conditional averaging over instantaneous swirling strength in each rotational motion core. Similarly, standardization is performed against local depth-averaged strength in each section.
From Fig. 7 , one can see relatively similar vertical distributions among different sections. For both prograde ( Fig. 7 a) and retrograde ( Fig. 7 b) spanwise rotational motions,Λp(r) (y)/<Λp(r) (y)>shows a monotonically decreasing trend withy/Hin all sections.Similar to the difference observed in the radii characteristics between decelerating and uniform open-channel flows (see Fig. 6 ),the wall-normal trends of the normalized swirling strength in decelerating open-channel flow are also more homogenized than those in uniform open-channel flow. The homogenised characteristic of decelerating open-channel flow may be due to decreasing streamwise velocity and increasing water depth and the positive wall-normal velocity, which increases the mixing effect of spanwise rotational motions in the wall-normal direction.
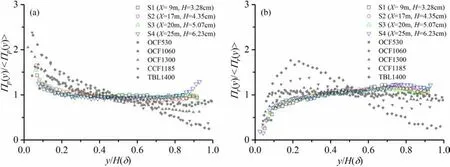
Fig. 5. Normalized population densities of prograde ( a ) and retrograde rotational motions ( b ). Open symbols are the results of current decelerating open-channel flows.Closed symbols are results of other flow types from the literature: uniform open-channel (OCF530 and OCF1060 from Chen et al. [27] , OCF1300 from Zhong et al. [32] );closed channel (CCF1185), and turbulent boundary layer (TBL1400) from Wu and Christensen [25] . The following numbers in these legends denote the friction Reynolds number.

Fig. 6. Normalized radii of prograde ( a ) and retrograde ( b ) rotational motions. Uniform open-channel results denoted with closed symbols (OCF530 and OCF1060 with the subsequent number indicating the friction Reynolds number) are from Chen et al. [27] .

Fig. 7. Normalized swirling strength of prograde ( a ) and retrograde rotational motions ( b ). Uniform open-channel results denoted with closed symbols (OCF530 and OCF1060 with the subsequent number indicating the friction Reynolds number) are from Chen et al. [27] .
By taking the instantaneous streamwise/wall-normal velocity at the core position as the instantaneous streamwise /wall-normal convection velocity for a given spanwise rotational motion, a conditional average can be further used to obtain the vertical distributions of the mean streamwise convection velocity,Ucp(r)(y), upward wall-normal convection velocity,Vcpu(ru)(y), and downward wall-normal convection velocity,Vcpd(rd)(y). Standardisation is performed against the depth-averaged value in each section. The results are shown in Figs. 8 –10 .
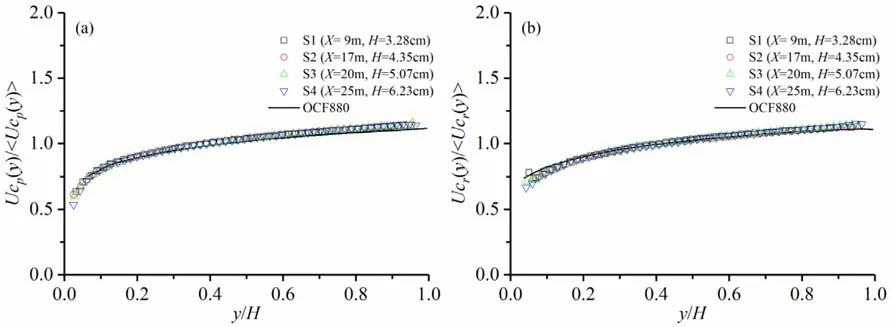
Fig. 8. Normalised streamwise convection velocities of prograde ( a ) and retrograde motions ( b ). Uniform open-channel results (OCF880 with the subsequent number indicating the friction Reynolds number) are from Zhong et al. [32] .

Fig. 9. Normalised wall-normal convection velocities of prograde motions: ( a ) Upward; ( b ) Downward.
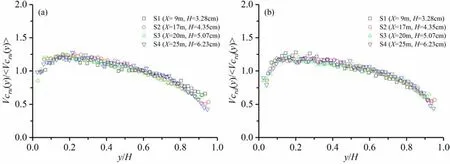
Fig. 10. Normalised wall-normal convection velocities of retrograde motions: ( a ) Upward; ( b ) Downward.
One can see that all convection velocity components show apparent similarity among different sections. The streamwise convection velocities of both prograde ( Fig. 8 a) and retrograde ( Fig. 8 b)motions increase monotonically withy/Hin all sections along with the water depth. Moreover, the results of streamwise convection velocity of rotational motions in uniform open-channel flow from Zhong et al. [32] are also cited, represented by a solid line in the figures. It can be seen that the vertical distributions of streamwise convection velocity of spanwise rotational motions in decelerating open-channel flow are very close to those in the uniform openchannel flow. In contrast, the wall-normal convection velocities for both prograde and retrograde motions, either upward ( Figs. 9 a and 10 a) or downward ( Figs. 9 b and 10 b), decrease monotonically withy/Hin all sections. No noticeable difference between prograde and retrograde motions can be seen. The downward motion seems to be slightly faster than the upward one.
The above analysis indicates that, when normalised against local depth-averaged value, the wall-normal distributions of density,size, strength, and velocity for spanwise rotational motions show no noticeable difference among the four sections. Self-similar characteristics seem to prevail independently of the distances from the flume entrance. That is plausibly due to the self-similar formation mechanism of coherent structures, which has been widely used in turbulence models [34] . For instance, Adrian et al. [35] proposed that the growing hairpins are consistent with the attached eddy hypothesis. The linear growth rate of the hairpins in a packet supports their self-similarity features. While the self-similarity of coherent structures has long been verified in different flow types,more work needs to be done for the decelerating open-channel flow considered here.
In decelerating open-channel flows, spanwise rotational motions prevail in different sections along the main flow direction.Major parameters of the spanwise rotational motions, e.g., density,size, strength, and convection velocity, change as the flow proceeds. However, when normalized with the local depth-averaged value, the difference diminishes among different test sections. Several self-similar trends remain unchanged when the flow advances.These trends include the following findings.
(1) The population densities decrease gradually for prograde motions but increase for retrograde motions along with the water depth except in the near-surface region.
(2) The radii are insensitive toy/Hwhile the swirling strength decreases withy/H.
(3) The population streamwise convection velocities, increase withy/H, and wall-normal convection velocity shows the opposite trend.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgments
The study is financially supported by the National Natural Science Foundation of China (Grant No. 51679020 ) and the Science and Technology Research Program of Chongqing Municipal Education Commission (Grant No. KJQN202100731).
杂志排行
Theoretical & Applied Mechanics Letters的其它文章
- Useful zero friction simulations for assessing MBS codes Pascal’s formula giving wheelsets frequency for zero wheel-rail friction
- Importance of induced magnetic field and exponential heat source on convective flow of Casson fluid in a micro-channel via AGM
- Optimal thermal design of anisotropic plates with arbitrary cutouts using genetic algorithm
- Optimal patching locations and orientations for maximum energy harvesting efficiency of ultrathin flexible piezoelectric devices mounted on heart surface
- Similarity solutions of Prandtl mixing length modelled two dimensional turbulent boundary layer equations
- Numerical simulation of droplet coalescence based on the SPH method
