Numerical simulation of droplet coalescence based on the SPH method
2022-08-26KaiwenGuTieqiangGangLijieChen
Kaiwen Gu, Tieqiang Gang , Lijie Chen
School of Aerospace Engineering, Xiamen University, Xiamen 3610 0 0, China
Keywords:SPH method CSF model Tangential force Droplet
ABSTRACT In this paper, the smoothed particle hydrodynamics (SPH) method is employed in modeling and numerical simulation of droplet coalescence. Considering the effect of tangential force on boundary material,besides normal force, tangential force is also introduced in the continuum surface force (CSF) model. The formation of droplet, the coalescence processes of two droplets and three droplets are simulated by the modified CSF model. The validity of the modified model is verified from the aspects of the morphological change of the droplet, the smoothness of free surface and the conservation of the centroid of the system.Compared with finite element method, the results of the modified CSF model show that tangential force plays a crucial role in the CSF model when dealing with model boundary with curves and sharp angles.
Surface tension is a force that only exists at the surface of liquid or the interface of insoluble liquids, and it has an important physical effect of reducing the surface area as much as possible. The simulation of surface tension involves free surfaces, deformation and motion boundaries [ 1 , 2 ], however, most of numerical methods for computational fluid dynamics cannot address these problems efficiently. For example, when dealing with the distortion of the grid caused by interface deformation, the stability and accuracy of numerical methods will be affected by grid dependency [3] if finite element method or finite volume method is employed. As a meshless Lagrangian particle method, smoothed particle hydrodynamics(SPH) uses the smooth function to interpolate and discretize the system, and describes the state of system by a set of particle nodes that carry physical information. Since there is no need to establish connections among particles by grids, problems caused by grid dependency can be avoided effectively.
So far, there are two main surface tension models applied in the SPH method: The inter-particle interaction force (IIF) model and the continuum surface force (CSF) model.
The IIF model constructs surface tension by applying the interaction force among molecules in a microscopic scale. Nugent et al.[4] first applied the SPH method to van der Waals fluids and simulated the oscillation of a droplet subjected to surface tension. Although the droplet oscillation phenomenon can be simulated, the aggregation of particles occurs. By using artificial stress method,Meleán et al. [5] simulated the collision aggregation of van der Waals fluid droplets at low Weber number, in which the particle aggregation is eliminated phenomenon. Tartakovsky et al. [6] introduced a new cosine function force about the distance between two fluid particles, which is a repulsive force when the particles are close to each other, and an attractive force when they are far away.The surface tension can also be simulated by this force. Akinci et al. [7] proposed a new surface tension force and a new fluidsolid adhesion force, which improved the handling of fluid-air and fluid-solid interfaces, and further addressed the particle-clustering problem in SPH simulations. However, the interaction force is computed by empirical formulas where some empirical parameters are difficult to determine. Also, the numerical result is hard to correspond to the macroscopic physical quantity. Moreover, the area of free surface cannot approach the minimization only based on the symmetrical interaction force.
The CSF model was first proposed by Brackbill et al. [8] .Hashemi et al. [9] used an immersed boundary method to convert the surface tension applied on boundary to the volume force of surrounding liquid. This conversion still maintains the conservation of momentum. This model requires an additional quantity,known as a color field, to find the curvature and normal of the surface particles. And a threshold parameter is introduced to identify the particles on free surface. The obtained surface tension is added to the Navier-Stokes equation as a volume force. The CSF model expresses liquid interfaces with different properties as transition regions with thickness, without interface reconstruction, and simplifies surface tension calculations, which can better model 2D and 3D liquids. The surface tension coefficient in this model is assumed to be constant, but the fact does not favor it. In 20 0 0, Morris et al.[10] first introduced the CSF model to the SPH method to simulate two-phase flows including surface tension. The simulation result is better than the grid-based finite volume method. Müller et al.[11] proposed a color function to Morris’s method to simplify calculations and their research did not consider the tangential force.Hu et al. [12] proposed a multi-phase SPH method considering a slightly different viscosity within a layer near the interface compared to the bulk, in which the inter-particle-averaged tangential stress by the slip length difference between the two phases was introduced into the method. Based on the classical CSF model without tangential surface tension, Dong et al. [13] proposed a virtual interface method to implement the contact angle in multiphase simulation of the gas-droplet-substrate system.
In the previous literature, most of the CSF model in SPH mainly considers the normal component of the surface tension, which is difficult to ensure the smoothness of the free surface, thus making the surface tension simulation failed. In addition, the absence of local surface particles because of model truncation leads to low computational accuracy of surface density and poor stability of simulation. The main work of this paper is to introduce tangential force to the CSF model to solve the above issues, which is illustrated by the examples of the coalescence processes of two-droplets and three-droplets. Our work is of great significance for better simulate the complex phenomenon of droplets coalescence and overcomes the shortcomings of traditional surface tension models.
The liquid flow needs to be described by the velocity fields,density fields and the pressure fields. The conservation equations of mass and momentum are expressed by:

If the particle number isN, Eqs. (1) and (2) can be rewritten by SPH approximations in the following form:

where 1 ≤i<Nand 1 ≤j<N.ρi,vi,xi,Piandηiare the density,velocity, position, pressure and kinematic viscosity of thei-th fixed particle, respectively.mj,ρj,vj,xjandPjare the mass, density,velocity, position and pressure of thej-th neighboring particle, respectively.
To calculate surface tension with the CSF model [8] , an additional quantity known as a color field should be introduced. The value of color field is 1 at the particle location and 0 at any other location in the space (outside the liquid). SPH approximations form of the color field is:

whereCsiis the value of the color field at thei-th fixed particle,andCsjis the value of the color field at thej-th neighboring particle.

whereftiis the tangential component of the force exerted by thej-th particle on thei-th particle andλis correction factor that adjusts the magnitude of tangential force according to the normal difference between particlesiandj.
From Eq. (8) , the tangential forceftiwill reduce the normal difference between thei-th fixed particle and thej-th neighboring particle and so as to move fluid from regions of low surface tension to higher surface tension. If this force is applied to all particles, the curvature of free surface can be reduced to minimize the area. The SPH approximation form of tangential forceftican be expressed as:

Fig. 1. The flow chart of the SPH calculations and post process.

To plot simulation results in graphical form, C ++ language and OpenGL are used to program. The whole process of the SPH calculations and post process is shown in Fig. 1 .
In this section, all the numerical simulations are performed in the SI unit system. Before simulating droplets coalescence, the formation of droplet is simulated to obtain round droplets. The formation process is shown in Fig. 2 . Before the droplet shrinks, its initial shape is square ( Fig. 2 a). Then, under the action of surface tension, the four sides of the droplet appear concave in the middle,and the four corners become sharper ( Fig. 2 b and 2c). The particle distribution at the corners is relatively coarse from that inside the droplet ( Fig. 2 d). Because of unbalanced force at the free surface,the particles move from the coarse particle corner to the dense area. The tangential force promotes to move particles to dense particle area, which makes sharp corners disappear and droplet deform close to round ( Fig. 2 d-2f).
For contrasts, the simulation results of the classical CSF model under the same initial conditions are given in Fig. 3 . In the early stage of simulation, the shrinkage process of the square droplet is similar to that by the modified CSF model ( Fig. 3 a-3c). However, as the simulation continues, the sharp corners do not appear smooth only under the action of the normal surface tension ( Fig. 3 d and 3e). After the same iterations of 10 0 0 0 as the modified CSF, the free surface is not convergent to a smooth round state ( Fig. 3 f).Even if the number of iterations continues to increase, the sharp angles always exist at the free surface. In summary, the classical CSF model only considering the normal force cannot promote the material flow at the free surface effectively during the droplet deformation.
On the basis of CSF model, tangential force is introduced to simulate the coalescence process of two droplets with different diameters. The initial velocities of the two droplets are zero and the gravity is ignored. The coalescence process is shown in Fig. 4 .When they are nearly contacting ( Fig. 4 a), their free surfaces are squeezed into sharp angles. With the expansion of the contact surface and the gradual disappearance of the sharp angles ( Fig. 4 b-4d), the material exchange at the contact surface is accelerated,and the two droplets gradually coalesce into a whole. After fully coalescence ( Fig. 4 e), the sharp corners disappear completely, and the material exchange between two droplets transforms into a material flow within the single coalescence droplet. Later, the free surface of this coalescence droplet becomes smoother under surface tension. Finally, the material flow inside the coalescence droplet tends to be stable and the droplet appears nearly round ( Fig. 4 f).It is clear that the coalescence process of the two droplets can be well reflected by the modified CSF model.
Under the same initial conditions, the simulation process by using the classical CSF model without considering tangential force is shown in Fig. 5 . In the early stage of simulation, the contact surface and sharp angles of the two droplets do not change significantly with the increase of iterations, and there is no obvious material exchange ( Fig. 5 a and 5b). As the simulation continues,the two droplets begin to exchange materials at the contact surface ( Fig. 5 c), but their free surfaces appear less smooth gradually.With the expansion of the contact surface, the sharp angles disappear completely, yet the problem of unsmooth free surface becomes more serious ( Fig. 5 d). The two droplets cannot completely coalesce and tend to disperse ( Fig. 5 e), and several gaps can be found in the area of their contact surface. Eventually, the whole disintegrates into several small parts with irregular shape ( Fig. 5 f),and the instability of surface tension obviously exists.

Fig. 2. Formation process of droplet with tangential force (961 particles). Each frame represents a time step of 10 -8 s.

Fig. 3. Formation process of droplet without tangential force (961 particles). Each frame represents a time step of 10 -8 s.

Fig. 4. Coalescence process of two droplets without tangential force (1130 particles). Each frame represents a time step of 10 -8 s.

Fig. 5. Coalescence process of two droplets without tangential force (1130 particles). Each frame represents a time step of 10-8 s.

Fig. 6. The coalescence process of two droplets simulated by Surface Evolver. ( a ) The initial state. ( b ) The result after 80 0 0 iterations.

Fig. 7. Coalescence process of three droplets with tangential force (1452 particles). Each frame represents a time step of 10-8 s.
For the initial states and conditions set in this paper, the two droplets should coalesce into a complete droplet instead of dissipating. So the simulation results of the classical CSF model without considering tangential force are obviously unreasonable. It can be drawn that the tangential force promotes the material exchange at the contact surface and the coalescence of two droplets, and the modified CSF model considering tangential force in this paper can deal with the problem of less smooth free surface well and better simulate the coalescence process of two droplets.
To make a comparison,SurfaceEvolver(developed by Brakke Ken) is also adopted to perform simulations under the same initial conditions of SPH. The surface is defined by vertices and edges,then this program evolves the surface towards minimal energy by a gradient method. For the convenience of simulations, the two droplets are partially coalesced and sharp angles are formed at the initial state ( Fig. 6 a). As the number of iterations increasing to 80 0 0, the contact surface of the two droplets expands. Compared with the SPH method, 80 0 0-steps of iteration is enough, but we can see that the sharp angles change slightly and there is no tend of coalescence for the two droplets ( Fig. 6 b). Even if the number of iterations continues to increase, the basic shape mode of the two droplets is similar to that of Fig. 6 b and the sharp angles always exist. So the further coalescence process cannot be revealed by usingSurfaceEvolver. It reflects thatSurfaceEvolver, which calculates the minimum curved surfaces based on finite element method, cannot simulate droplets coalescence process with sharp angles.

Fig. 8. Coalescence process of three droplets without tangential force (1452 particles). Each frame represents a time step of 10-8 s.
Furthermore, for three droplets with the same diameter, the coalescence process is simulated by the CSF model considering tangential force. Similarly, the initial velocities of droplets are zero and the gravity is ignored. The coalescence process by our modified method is shown in Fig. 7 . The initial state is the three droplets begin to contact, the free surfaces of them form a sharp gap in the middle ( Fig. 7 a). With the expansion of the contact surfaces among droplets, the sharp angles are gradually squeezed( Fig. 7 b), disappear ( Fig. 7 c) and a smoother round hole in the middle forms ( Fig. 7 c). As the iteration proceeds, the hole among the three droplets shrinks until it disappears ( Fig. 7 d). After that,the boundaries among the droplets completely disappear and the three droplets begin to form a whole. As the process continues, the surface of the coalescence droplet gradually deceases by the influence of surface tension ( Fig. 7 e and 7f). When the three droplets fully coalesce into a large droplet ( Fig. 7 e), a flow of material begins inside, and the shape of the droplet changes under the action of surface tension. Finally, the internal material flow of the coalescence droplet tends to be stable, the free surface becomes smooth and nearly round ( Fig. 7 f). The coalescence process of the three droplets is also be well represented by the modified CSF model.
Under the same initial conditions, the simulation results of the classical CSF model are given in Fig. 8 for contrasts. In the early stage of the simulation, there is no obvious change on the sharp gap and the contact surface among the three droplets ( Fig. 8 a and 8b). With the increase of the iterations, the three droplets begin to deform as they continue to squeeze ( Fig. 8 c and 8d). In addition, the free surface appears not smooth anymore and several irregular shaped gaps appear. No fully coalescence droplet is found.Finally, the whole droplet system breaks up due to the instability of surface tension ( Fig. 8 e and 8f). It is found that the three droplets cannot coalesce to form a whole droplet only with the normal force component, and tangential force really plays an important role in maintaining the stability of surface tension and addressing the problem of non-smooth free surface. In addition, because of the sharp gap, the simulation cannot be performed bySurfaceEvolver.
The variation of the centroid position during three droplets coalescence is shown in Fig. 9 . The centroid offsets of the system simulated by the modified CSF model, both in theX-axis direction( Fig. 9 a) andY-axis direction ( Fig. 9 b), are smaller than those by the traditional CSF model, which reflects that the centroid of the system is much closer to conservation.
Compare with Refs. [ 11 , 13 ], the main novelty of this paper is to introduce tangential force into the CSF model to solve these issues, which is illustrated by the examples of the coalescence processes of two-droplets and three-droplets. Different from Ref.[12] , the tangential force applied in this paper is based on the normal difference among particles instead of the slip length difference between the two phases, which is more convenient for calculation. It is found that the introduce of tangential force can promote the expansion of the contact surface and the material exchange at the contact surface so as to reflect reasonable coalescence process of droplets. Besides, the tangential force helps to maintain the stability of surface tension and the conservation of the centroid of the system, eliminate the sharp angles,and make free surface smoother, which ensures the stability of simulations.
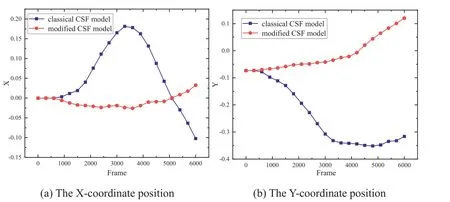
Fig. 9. Variation of centroid position during three droplets coalescence. (a) The X-coordinate position. (b) The Y-coordinate position.
Declaration of Competing Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
杂志排行
Theoretical & Applied Mechanics Letters的其它文章
- Useful zero friction simulations for assessing MBS codes Pascal’s formula giving wheelsets frequency for zero wheel-rail friction
- Importance of induced magnetic field and exponential heat source on convective flow of Casson fluid in a micro-channel via AGM
- Optimal thermal design of anisotropic plates with arbitrary cutouts using genetic algorithm
- Optimal patching locations and orientations for maximum energy harvesting efficiency of ultrathin flexible piezoelectric devices mounted on heart surface
- Similarity solutions of Prandtl mixing length modelled two dimensional turbulent boundary layer equations
- Thermal energy storage inside the chamber with a brick wall using the phase change process of paraffinic materials: A numerical simulation
