Optimal thermal design of anisotropic plates with arbitrary cutouts using genetic algorithm

Mohmmd Jfri ,, Soheil Yri , Mohmmd Jfri

a Mechanical Engineering Department, Shahrood University of Technology, Shahrood, Iran

b Faculty of Mechanical and Mechatronics Engineering, Shahrood University of Technology, Shahrood, Iran

Keywords:Anisotropic materials Perforated plate Optimization Genetic algorithm Thermal stress Complex variable method Conformal mapping

ABSTRACT Anisotropic plates in different applications may have geometric defects such as openings and cracks. The presence of the opening disturbs the heat flow, which creates significant thermal stress around the opening. When the heat flux is high enough, these extreme stresses can lead to structural failure. This article aims to obtain the optimal parameters for achieving the minimum value of the normalized stress near the cutout’s boundary in perforated anisotropic plates utilizing the genetic algorithm. Optimization parameters include the curvature of opening’s corners, orientation angle of opening, fibers angle, heat flux angle,and opening’s elongation. The plate is under heat flux, and the opening’s border is thermally insulated.The stress distribution around the opening is calculated using Lekhnitskii’s complex variable method and complex potential functions. The genetic algorithm is then implemented to find the optimal values for design parameters. The results show that by selecting the optimal parameters related to the anisotropic material and the opening’s geometry, the stress intensity factor of the perforated anisotropic plates is remarkably reduced. Furthermore, this optimization algorithm can be extended to find the optimized parameters and achieve the optimal designs in anisotropic and isotropic perforated plates under thermal loadings.

Anisotropic materials, such as composites, due to their special mechanical and thermal characteristics, including low weight, high strength, thermal endurance, design capability, and prolonged lifespan compared to other materials, have been hugely considered by engineers and artisans. Applications of these materials include aerospace, automotive, construction, marine, electricity, and railway engineering. Preventing structural failure caused by stresses created in the geometric defects is of significant importance in the designing stages. An opening is one of the types of discontinuities in the structure. Since the presence of holes in structures causes a change in their behavior, it is vital to study and analyze systems with openings and examine the effect of different types of openings. Analyzing thermal stress components is of high importance in the mechanics of solids. Furthermore, because structures are under high thermal loads in many applications, predicting the behavior of structures under this type of stress and calculating the value, the impact, and the location of maximum stresses is necessary to reach a logical and realistic design. Thermal stress occurs when the thermal field is disturbed due to an opening. In this regard, studying the stress concentration around cutouts in elastic materials under heat flow and optimization of these points causes the least amount of stress in the opening area, which is very important in the advanced design of engineering structures.

Numerous studies have been performed on the thermoelastic problem of plates containing geometric defects using Lekhnitskii’s complex variable method. Part of this research involves investigating the effect of openings, and the other part involves studying the presence of cracks in infinite plates under heat flow.Florence and Goodier [1] are the founders of theories for solving two-dimensional (2D) thermoelastic problems using the complex variable technique. Florence and Goodier solved the thermal stresses analysis problem for isotropic elastic plates containing circular and elliptical openings using the complex variable technique.Chen [2] obtained an analytical expression for the stress components near the circular and elliptical insulated openings in the orthotropic plates subjected to uniform heat flow implementing the complex variable technique. Using the least-squares method at the boundary points, Rao et al. [ 3 , 4 ] studied the temperature and inplane stress distribution in a rectangular elastic plate containing a circular opening. Nisitani et al. [5] proposed a solution for a plate with a circular opening subjected to uniform heat flow.

Numerous high-quality studies have examined the plasticity of the crack tip. In recent decades, researchers have proposed several linear and nonlinear fracture mechanics parameters to address this type of damage [6] . Thermal stress, temperature distribution, stress intensity factor, and heat flux singularity for infinite isotropic plate subjected to uniform heat flow with symmetrical cracks around the rhombus opening were analyzed by Norio et al.[7] . Hwu [8] solved the thermal stresses analysis problem in a uniform anisotropic body disturbed by an oval opening or crack. Using Lekhnitskii’s complex potential technique, Tarn et al. [9] studied the in-plane thermal stresses and strain in an infinite anisotropic elastic body with a rigid inclusion. Chao and Shen [10] examined temperature and stress in an infinite anisotropic plate containing an oval opening subjected to uniform heat flux.

Using Stroh’s formulation, Chao and Gao [11] presented an analytical solution for an oval cutout on an infinite anisotropic plate subjected to heat flow. They implemented conformal mapping techniques to derive a formulation for examining the stress distribution. Zhang et al. [12] studied the exact solution for thermal stress analysis in FGM plates containing circular openings. In an article by Hasbeh and Wang [13] , the equations for solving a twodimensional thermoelastic problem of a plate containing a cutout are described. The plate was made of isotropic and homogeneous linear elastic material, which followed Hooke’s law. The complex variable method was used, and the complex potential functions for various thermal and boundary conditions were obtained. The general solution of the problem was presented under uniform heat flux or in the presence of a concentrated heat source.

In a study by Wang et al. [14] , thermal stress induce deformation was investigated using the finite element method. The stress field around a triangular hole in an infinite isotropic plate subjected to uniform heat flux was investigated by Jafari et al.[15] based on the two-dimensional steady-state thermoelasticity theory assuming that the hole boundary was thermally insulated.They also analyzed and examined the effect of determining parameters on the stress distribution [16] . Using the complex potential method, Hu and Chen [17] derived the explicit forms for mechanical, electrical, and magnetic fields in a problem involving an oval cavity embedded in a reinforced magnetoelectroelastic (MEE) material.

Moure et al. [18] investigated the crack growth process in composite multilayers containing openings under combined mechanical and thermal loadings and evaluated the effect of thermal loading on stress concentration and the failure process. Jiang et al. [19] presented a three-dimensional analysis for the thermodynamic problem of a double-layer structure with a local heat source. Rasouli and Jafari [20] developed Lekhnitskii’s complex variable method and used the conformal mapping technique to obtain the stress distribution around an elliptical hole in an infinite anisotropic plate under uniform heat flux. In addition, they investigated the effect of important parameters on stress distribution. Jafari and Jafari [21] used the conformal mapping technique to calculate stress distribution around a triangular opening in anisotropic plates under heat flux. In another research by Jafari and Jafari [22] ,thermal stresses around a rectangular hole in an orthotropic plate were calculated. In that study, they examined various factors to find the amount and the location of the maximum thermal stress in perforated composite plates, assuming that the hole’s boundary is thermally insulated and the plate is under uniform heat flux.

Using the two-dimensional theory of elasticity and Muskhelishvili’s complex variable method, Patel and Desai [23] calculated the tangential stress concentration factor around an oval hole in a rectangular plate under in-plane loading. They used the conformal mapping technique and Cauchy’s integral formula to obtain stress functions. Muskhelishvili’s formula and the conformal mapping technique were also adapted by Li and Zheng [24] to determine the stress intensity factors of kinked cracks emanating from a hole. Qiao et al. [25] investigated the fatigue failure in composite laminates in the presence of notches. The obtained results showed that the damage progress under multi-axial fatigue loading could be significantly different from that under quasi-static loading.

Tan et al. [26] used the complex variable method to analyze the analytical stress distribution for rock masses containing holes with complex geometries. In addition, they developed and improved the mapping function method for six types of holes with typical shapes using optimization techniques. Zeighami and Jafari[27] presented a general solution for analyzing thermoelastic stress in asymmetric FG-CNTRC plates containing a central hole. They examined the effects of determining parameters on stress and moment resultants around the cutout using Lekhnitskii’s complex potential approach and conformal mapping function.

Another branch of research in the design of engineering structures is optimization problems and selecting optimal values of design variables governing the problem. Nowadays, the use of intelligent meta-heuristic algorithms in optimization has been considered and used by many researchers due to their desirable and appropriate performance. A research in this field was done by Sivakumar et al. [28] , who optimized multilayer composite plates containing elliptical openings using genetic algorithms. Their research considered the opening orientation, elongation, fibers angle, the layers’ material as design parameters, and the natural frequency as the design constraint in this algorithm. Cho and Rowlands[29] demonstrated the ability of the genetic algorithm to minimize stress concentration in composite layers containing openings.In this research, a specially developed genetic algorithm and finite element method were used to determine the cost function to minimize the concentration of stress around the opening.

Le-Manh and Le [30] proposed a methodology based on the genetic algorithm to present the optimal arrangement for composite layers subjected to transverse and compressive loading. Sharma et al. [31] investigated the optimal uniform load-bearing composite layers, including oval openings, using a genetic algorithm. In that study, they optimized the fiber angle and calculated the cost function using the Tsai-Hill failure criterion. Vosoughi and Gerist[32] proposed a new combination method of particle mass optimization, finite element, and continuous genetic algorithm to determine the damage of composite beams. First, they determined the equilibrium equations that govern composite beams using firstorder shear deformation theory (FSDT). Then they solved the equations with the corresponding boundary conditions using the FEM and used their method to determine the extent of the damage. To prove the efficiency of their method, they examined various parameters such as damage ratio, number of layers and damaged elements, and fiber angle of each layer.

Zhu et al. [33] optimized composite structures using a genetic algorithm and applied the Tsai-Hill failure criterion. Their focus was on reducing the structure’s weight and increasing the buckling load. They chose volumetric fiber failure and layer arrangement as design variables. Moussavian and Jafari [34] investigated the optimal design of composite multilayers containing quasi-square openings using three different models of optimization algorithms. They reduced stress concentration around the quasi-square opening by optimizing variables such as opening curvature, layer arrangement,and rotation angle. Jafari and Bayati [35] optimized the design of infinite composite plates with triangular openings using the dragonfly optimization method. Fiber angle, load angle, opening corners curvature, opening angle, and material type were considered as design variables.

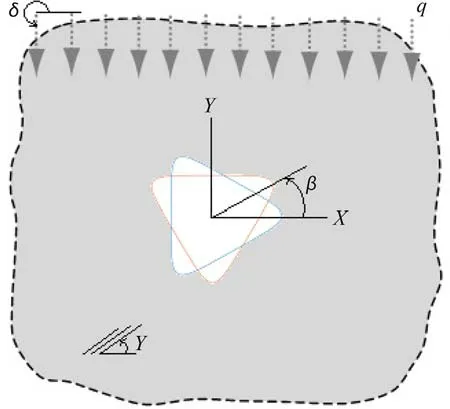
Fig. 1. A central hole embedded in an anisotropic plate subjected to heat flux [21] .

The present study reports the optimal thermal stress of perforated composite plates with a non-circular hole. Since in many industrial applications, anisotropic single-layers containing cutouts are subjected to heat flux, the need to analyze the thermal stresses in these plates and implement different methods to achieve the optimal design is fully felt. The result obtained in this study is based on a theoretical solution. It should be noted that in this research, since many parameters affect the amount and the location of the maximum thermal stress, the genetic algorithm has been used to optimize the desired parameters and achieve the lowest thermal stress. No study has ever optimized the thermal stresses induced by the uniform heat flux in an anisotropic single-layer elastic medium containing a non-circular hole. This research assumes that the stress and complex potential field around the opening are on an infinite and anisotropic plate. The plate is under uniform heat flux in the infinity, and the opening border is insulated. The Neumann boundary condition is applied. The stress distribution around the opening is calculated using complex potential functions and solving integral equations. The effect of essential parameters on thermal stress, such as opening rotation angle,opening corners curvature, fiber angle, heat flux angle, and opening elongation, has been investigated. This novel method led to accurate results. Hence it can be used for isotropic plates, composite laminates, and functionally graded (FGM) plates due to significant innovation and general flexibility of the obtained potential function.

The aim is to minimize the thermal stresses around the openings with arbitrary geometries in an anisotropic plate subjected to uniform heat flux and investigate various determining parameters,including opening rotation angle, opening elongation, opening corners curvature, heat flux, and fibers angle.

As illustrated in Fig. 1 , an infinite plate with an opening in the center is under heat flux. The applied heat flux has a magnitude ofqwith a direction at an angle ofδto thex-axis. The plate is considered to be homogeneous and linearly elastic, which satisfies Hooke’s general law. The fibers angle is arbitrary and denoted byγ. The hole is insulated, and its size is considered small enough compared to the dimensions of the plate. Hence, the plate can be assumed to be infinite. The hole direction is the rotation angle of the opening, and is denoted byβ.

The opening boundary is free from the external loads, and the Neumann boundary condition is considered. The heat flow is disturbed by the opening, which causes thermal stress around it.Since there is no heat source embedded in the plate, the location of the maximum stress resulted will be on the boundary of the opening [36] . In addition, due to the boundary conditions, the only stress component created at the opening’s boundary isσθ.The stress and strain components are considered to be in-plane,and the deformations assumed to be very small.

Complex potential functions are used to solve the problem. This method provides an effective tool for solving thermal stress problems. The complex variable technique is implemented for the mapping function. Applying this technique makes it easy to solve many problems that are very difficult to solve in other ways.

First, the infinite zone outside the opening is transferred to the outer region of a circle to extend and develop the analytical method of a circular opening for holes with different shapes and simplify the Cauchy integral formula. The conformal mapping function is defined as follows [37] :

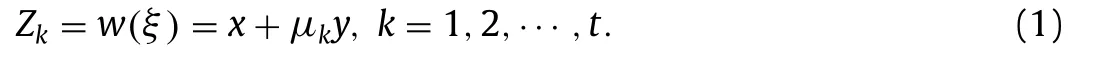
In Eq. (1) ,μkare the eigenvalues, whilexandyare on the opening plane and are defined as follows:

x=λ[ cosθ+ωcos(nθ)],

In Eq. (2) ,λdetermines the size of the hole,cdefines opening elongation or compression in the y-direction, parameterωspecifies the curvature of the opening corners, andndetermines the geometry of the opening. The mapping function can be rewritten as follows:

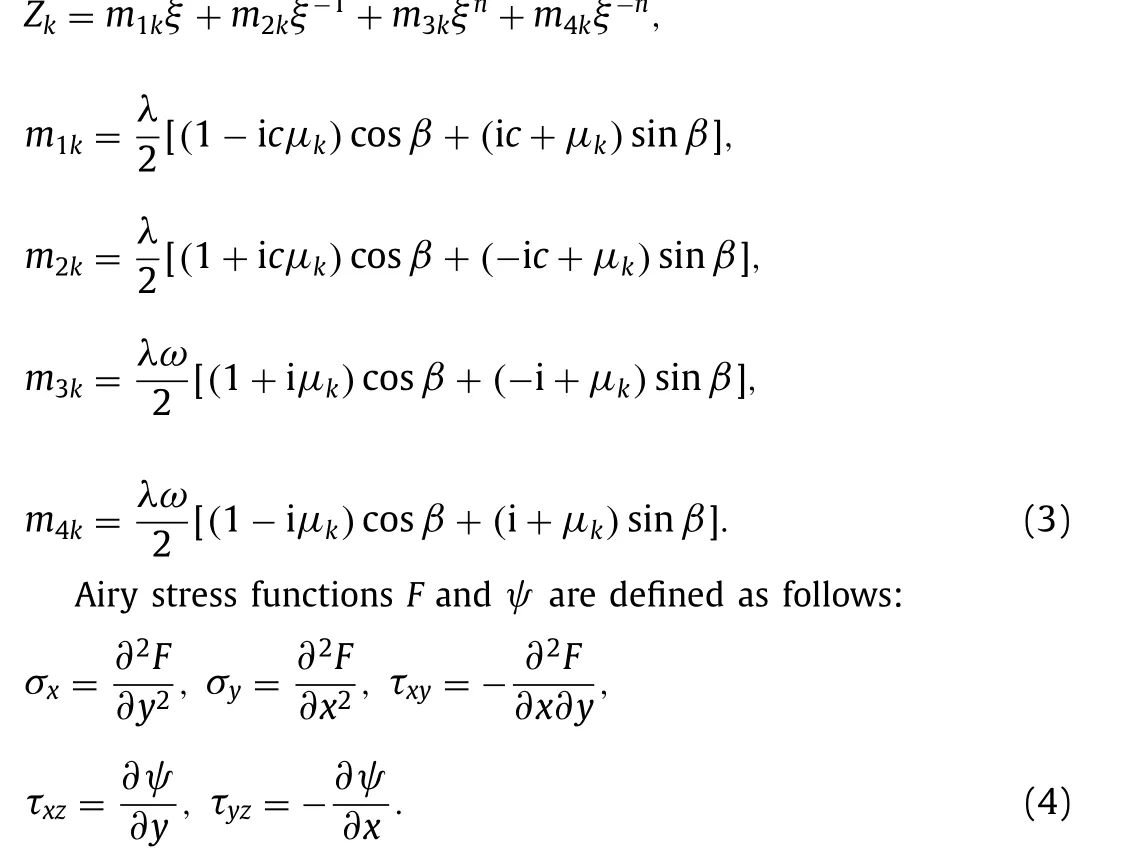
With introducing Airy stress functions and using compatibility relationships, two characteristic equations for orthotropic materials with regard to stress functions are obtained in the following form[36] :

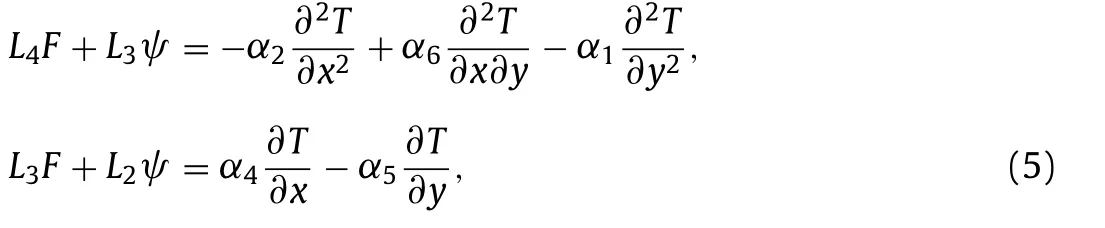
whereTis temperature,αiare quasi-vector components of thermal expansion coefficients in local coordinates, andL2,L3 and,L4 are differential operators with orders of 2, 3, and 4, respectively. These operators are as follows for in-plane stress mode:

The material is homogeneous and anisotropic. Also, there is no heat generation in the body. Hence, according to Fourier’s law, the thermal governing equation is as follows [36] :

Fig. 2. Tangential coordinate system at the cutout border.

Figure 2 shows the tangential coordinates and definition of the normal vector around each cutout.

There are no external loadings at the boundary of the opening.As a result, the mechanical boundary conditions will be written as follows:

By integrating from Eq. (15) and placing Eqs. (7) , (10) and(13) in it, the mechanical boundary conditions will be written as follows:

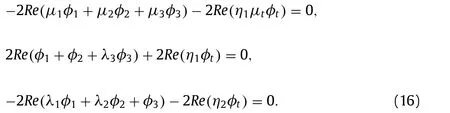
In order to compute the stress functionsφandφt, these matrices are introduced:

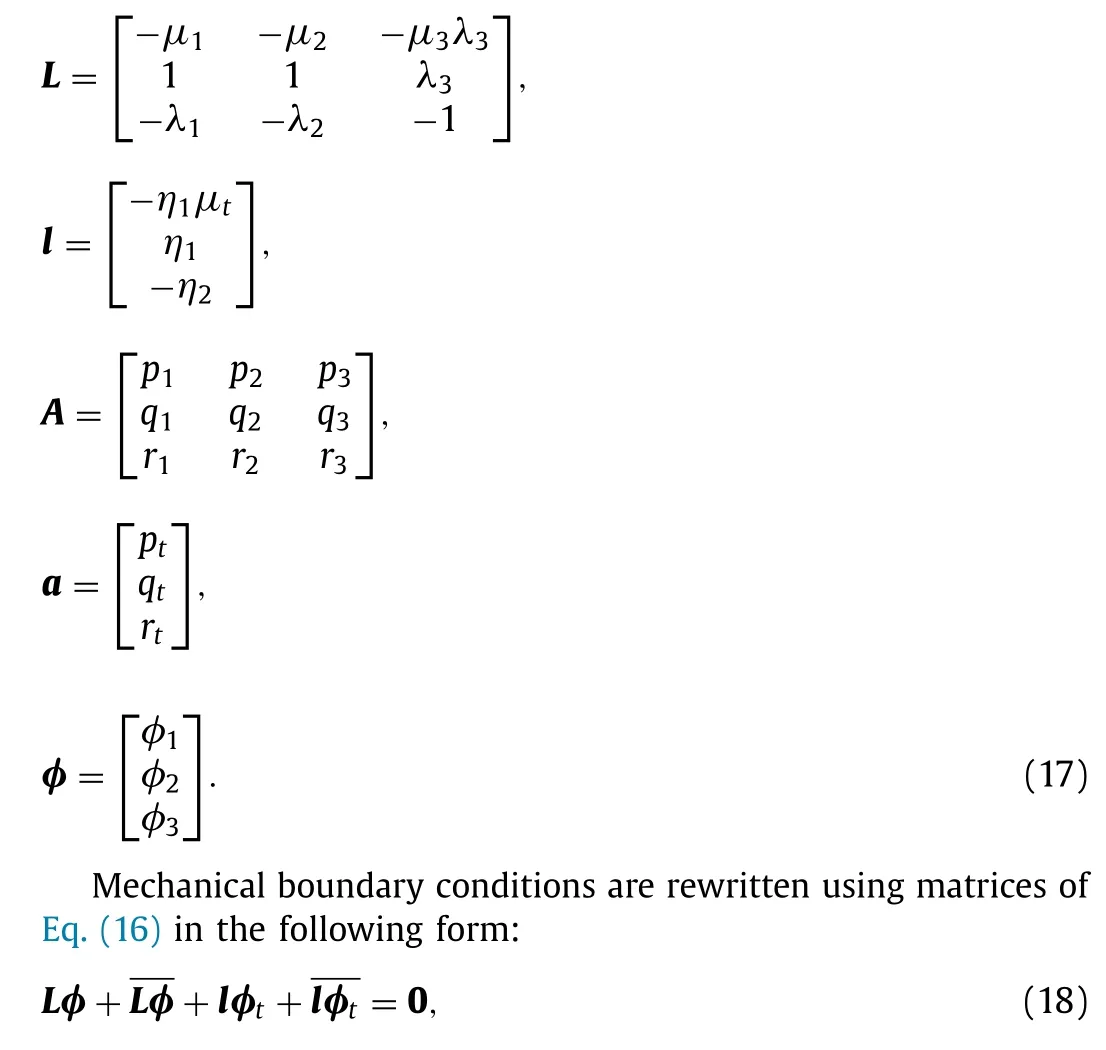
when the heat flux in the normal direction on the cutout boundary can be defined as a continuous function, the Neumann thermal boundary condition is used. The Neumann boundary condition will be as follows:

wherenis the normal vector on the cutout boundary, andq0is the continuous function of heat flux in the normal direction on the cutout boundary. Using Eqs. (13) and (19) can be written in terms ofφt. By integrating on the cutout boundary, the Neumann boundary condition will be written as follows:

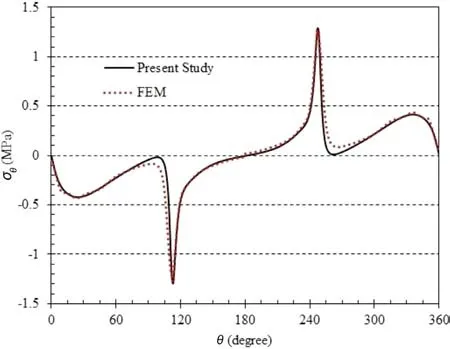
Fig. 3. Comparison of stress distribution ( σθ) on the edge of the triangular cutout obtained from the present study and FE method.

Therefore, according to Eq. (12) , thermal stresses are obtained.In this paper, the thermal stress is presented as a dimensionless quantity, which is calculated using Eq. (27) .

To assess the validity and accuracy of the present analytical approach, the results obtained from commercial FEM software ABAQUS were used. Figure 3 compares the results of stress distribution (σθ) on the edge of the triangular cutout in an orthotropic plate subjected to uniform heat flux. The results were obtained for an orthotropic plate made from AS/3501 graphite/epoxy composite.The mechanical properties of the material are presented in Table 1 .In the temperature range between 20 °C and around 500 °C, carbon fibers exhibit negative thermal expansion [38] . Additionally,the angle of the material fibers with respect to thex-axis is zero.Carbon fiber’s negative thermal expansion coefficient, coupled with its high modulus, allows the fabrication of composites with a nearzero thermal expansion coefficient when the fiber orientation is properly controlled [39] .

To satisfy the assumption of an infinite plate, the dimensions of the plate are assumed to be more than 20 times larger than the hole size. The hole’s rotation angle is zero and the corners’ curvature is 0.25. The heat flux is applied to the plate at an angle of 270 degrees to thex-axis. Four-node quadrilateral elements are used to mesh and analyze the plate with the hole in the center.Furthermore, mesh refinement has been conducted in the vicinity of the hole to improve the precision of the FE results. A total of 240 elements is set around the hole, providing convergence of the results for triangular cutout as well as quadrilateral and pentagonal. The comparison of the stress distribution is made for quadrilateral hole in Fig. 4 and pentagonal hole in Fig. 5 under the same circumstances. As shown in these figures, the results of the presented analytical approach are in good agreement with the results of the numerical solution.

The genetic algorithm, a branch of evolutionary algorithms and Darwin’s natural selection principle, is a computer search method based on optimization algorithms and is based on genes and chromosomes and inherited rules. The values of the optimization algorithms parameters have a remarkable effect on the convergence rate and the achievement of the optimal state of the objective function. Therefore, by modifying these parameters to their optimal values, higher efficiency of the algorithm can be achieved. Thissection presents the results of anisotropic plates containing openings with different shapes (triangular, quadrangular, and pentagonal).

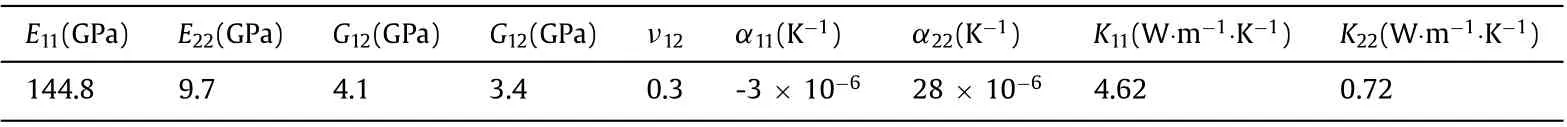
Table 1 Mechanical properties of Graphite/Epoxy (AS/3501) [21] .

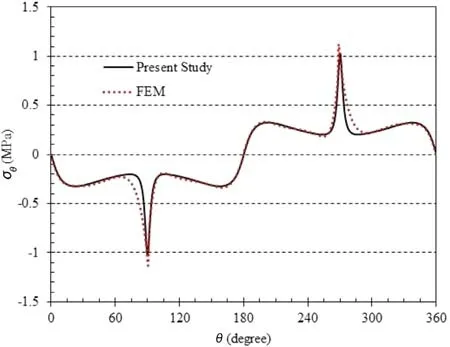
Fig. 4. Comparison of stress distribution ( σθ) on the edge of the quadrilateral cutout obtained from the present study and FE method.

Fig. 5. Comparison of stress distribution ( σθ) on the edge of the pentagonal cutout obtained from the present study and FE method.

The population size significantly affects the algorithm’s performance. If the population is too small, the possibility of forming the displacement operations will be very low, and just a tiny part of the domain will be explored. On the other hand, if the value is high, the algorithm’s speed will be too low. Some research also suggests that population size should be defined in terms of the problem type and its coding, and further excessive increase would be useless. In the following figures, the effect of population size on the convergence of the optimal cost function is investigated.Figure 6 is for the triangular opening mode, and Figs. 7 and 8 are for the quadrilateral and pentagonal opening modes, respectively.Table 2 shows the optimal values of the design variables and the optimal objective function in different values of population size.As can be seen, in the population of 50, the algorithm is caught in the local optimization due to the small population. It is noteworthy that in other populations shown, the algorithm converges to the optimal value of the objective function, and the difference is only in the time of convergence. Therefore, in all the results presented in this article, a population size of 100 is considered.

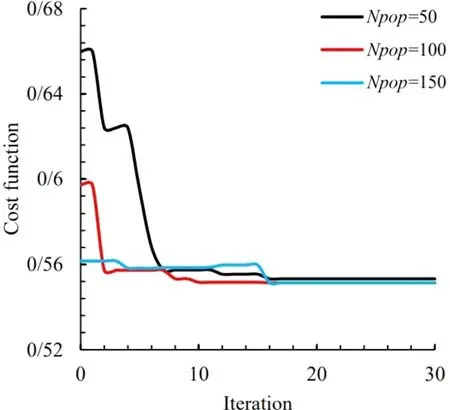
Fig. 6. Convergence of cost function with different population sizes in triangular cutout.

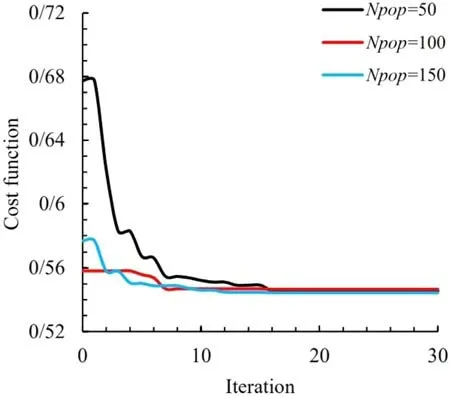
Fig. 7. Convergence of cost function with different population sizes in quadrangular cutout.

In this paper, the single-point combination method is used. The number of populations participating in the combination operation depends on the probability of the crossover. If the probability of crossover is zero, it means that the crossover operation is not performed, and if it is one, it means that all the chromosomes are involved in the combination. Usually, in analyses, the value of the crossover operator is considered between 0.5 and 0.9. Using Eq. (28) , the number of population on which the combination operation is performed is obtained.

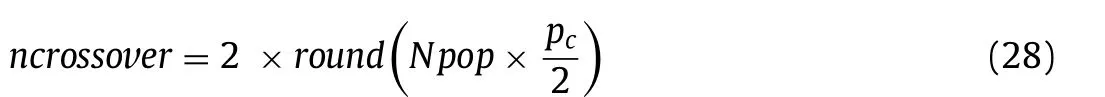
Table 2 Optimal values of the objective function and design variables in different population sizes.

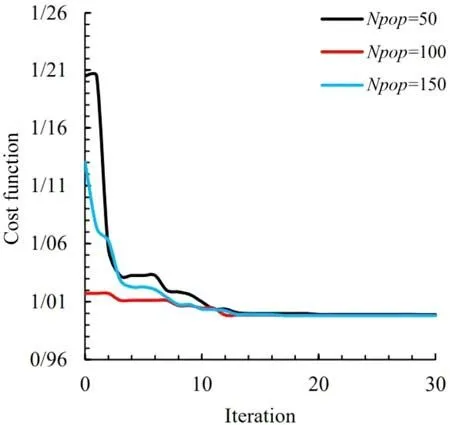
Fig. 8. Convergence of cost function with different population sizes in pentagonal cutout.

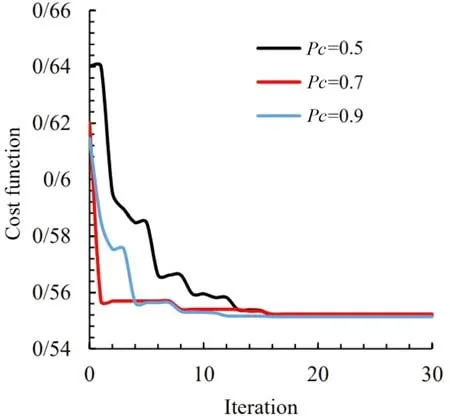
Fig. 9. Convergence of cost function for different values of p c in triangular cutout.

Where npop andpcare population size and probability of crossover, respectively. Figures 9 , 10 , and 11 , show the effect of crossover probability on the convergence of optimal cost function for triangular, quasi-square, and pentagonal openings, respectively,with a curvature ofω= 0.1 in the corners. Table 3 also shows the optimal values of the design variables and the optimal objective function in different values of probability of crossover. It can be seen that changing the crossover probability value has nearly no influence on the optimal amount of stress. Therefore, this parameter is considered equal to 0.7 in this article.

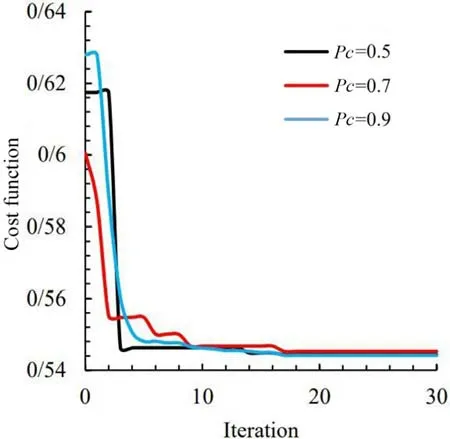
Fig. 10. Convergence of cost function for different values of p c in quadrangular cutout.

Fig. 11. Convergence of cost function for different values of p c in pentagonal cutout.

After applying the crossover operator and in order to avoid convergence to local optimal and to create population diversity, using the mutation operator, some obtained chromosomes are changed.This creates new chromosomes that may not have existed in the entire population. This operator also ensures that the probability of searching anywhere in the problem domain is never zero, regardless of the initial population dispersion. The mutation probability on chromosomes is usually considered to be about 0.5% to 3% [34] .Equation (29) indicates the number of populations involved in mu-tation.

Table 3 Optimal values of the objective function and design variables in different crossover probabilities.

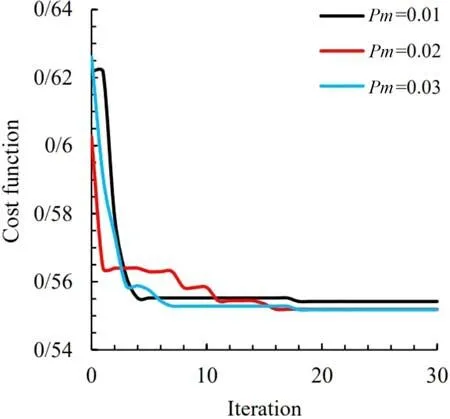
Fig. 12. Convergence of cost function for different values of p m in triangular cutout.

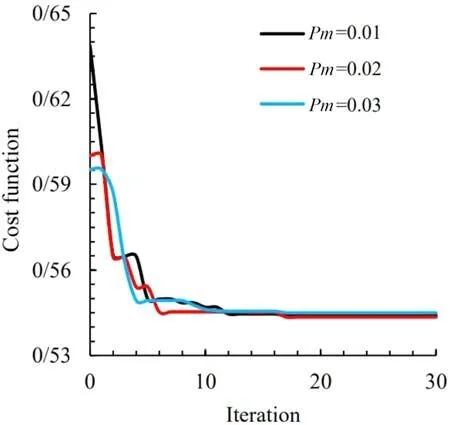
Fig. 13. Convergence of cost function for different values of p m in quadrangular cutout.

wherepmis mutation probability. Figures 12 , 13 , and 14 show the convergence rates of the cost function with different values of the mutation probability for triangular, quadrangular, and pentagonal holes, respectively, with corner curvature ofω= 0.1. Table 4 also shows the optimal values of the design variables and the optimal objective function. It can be seen that changing the amount of mutation probability has a minor influence on the optimal amount of stress. Hence, a mutation probability of 0.02 is considered in this paper.

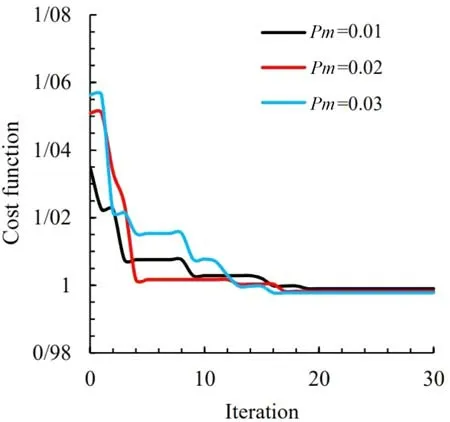
Fig. 14. Convergence of cost function for different values of p m in pentagonal cutout.

It is essential to find the maximum stress created and minimize its amount in designing plates. The highest value of the stress on the plate occurs in the area around the opening. In this study,when the maximum stress created on the edge of the opening reaches its minimum value, it is the desired stress, and the state where the maximum stress created reaches its maximum value is undesirable stress. Reaching the desired stress state can prevent material failure and increase the lifespan of the structure. The Genetic algorithm is implemented for optimizing the design variables and obtain the desired stress. In this paper, the effect of the opening corners curvature, heat flux angle, material fiber angle,and hole orientation angle on the maximum thermal stress created near triangular, quadrangular, and pentagonal openings is investigated using the genetic algorithm.

Theωparameter is defined to determine the sharpness or softness of the opening corners. In other words,ωrepresents the curvature of the opening corners, that increasing or decreasing it sharpens and softens the corners of the opening, respectively. Also,as the opening sides increase, the range ofωbecomes smaller. As shown in Fig. 15 , for openings with an odd number of sides (triangle and pentagon), asωdecreases and the opening corners become softer, the objective function decreases as expected, so that forω= 0, the opening takes deforms and turns into a circle. In this case, the value of the cost function also reaches the lowest possible amount. However, contrary to expectations, this situation is different for openings with an even number of sides. As shown in Fig. 15 , as the opening corners curvature increases, the diagrams for these openings behave differently. In other words, the diagram for openings with an even number of sides (quadrilateral) initially has a downward trend with increasing valueω, and then with increasing curvature, the amount of the cost function increases.

Table 4 Optimal values of the objective function and design variables in different mutation probabilities.

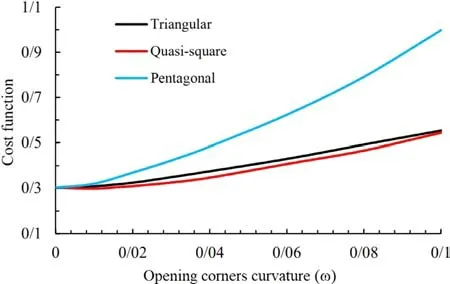
Fig. 15. Effect of opening corners curvature on optimum value of cost function for various shapes of cutout.

Table 5 Optimum values of design parameters and corresponding cost function in various corner curvatures.

Table 5 shows the optimal values of the design parameters and the corresponding thermal stress created. As can be seen, in triangular and pentagonal openings, the lowest values occur in the case of circular openings (ω= 0), and the value of their optimal objective function is 0.3026, while the lowest values of the optimal objective functions for square openings occur in the curvature ofω= 0.01,and its value is equal to 0.2982. Figures 16 , 17 , and 18 show how the objective function converges for triangular, quadrangular, and pentagonal openings, respectively. The opening corners curvature value isω= 0.1 in these diagrams.

One critical parameter in the amount and distribution of stress around the opening in anisotropic plates is the fibers angle (γ).The angle of the material fibers is the angle that these fibers make with the horizon axis. As shown in the figure, the optimal stress diagram with regard to fiber’s angle is a periodic function with a periodicity of 90 °. According to Fig. 19 , the optimal stress and undesirable stress occur at the fiber angles close toγ= 0 andγ= 90,respectively. As can be seen, the diagrams of the triangular and pentagonal openings coincide precisely.

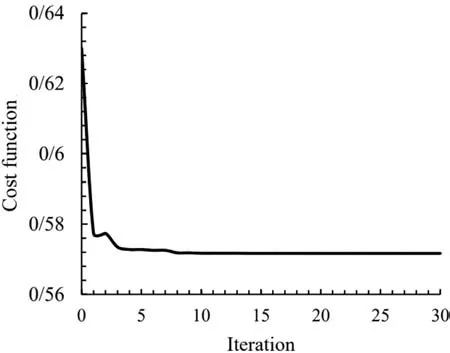
Fig. 16. Convergence of the objective function for triangular cutout.

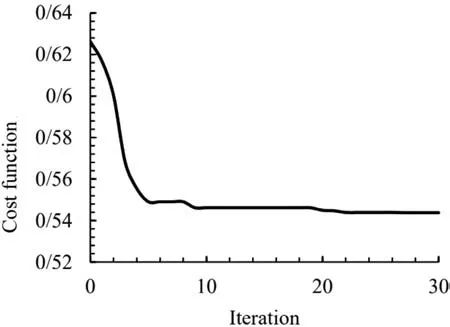
Fig. 17. convergence of the objective function for quadrangular cutout.

Fig. 18. convergence of the objective function for pentagonal cutout.

Fig. 19. Effect of fiber angle on optimum value of cost function in various shapes of cutout.

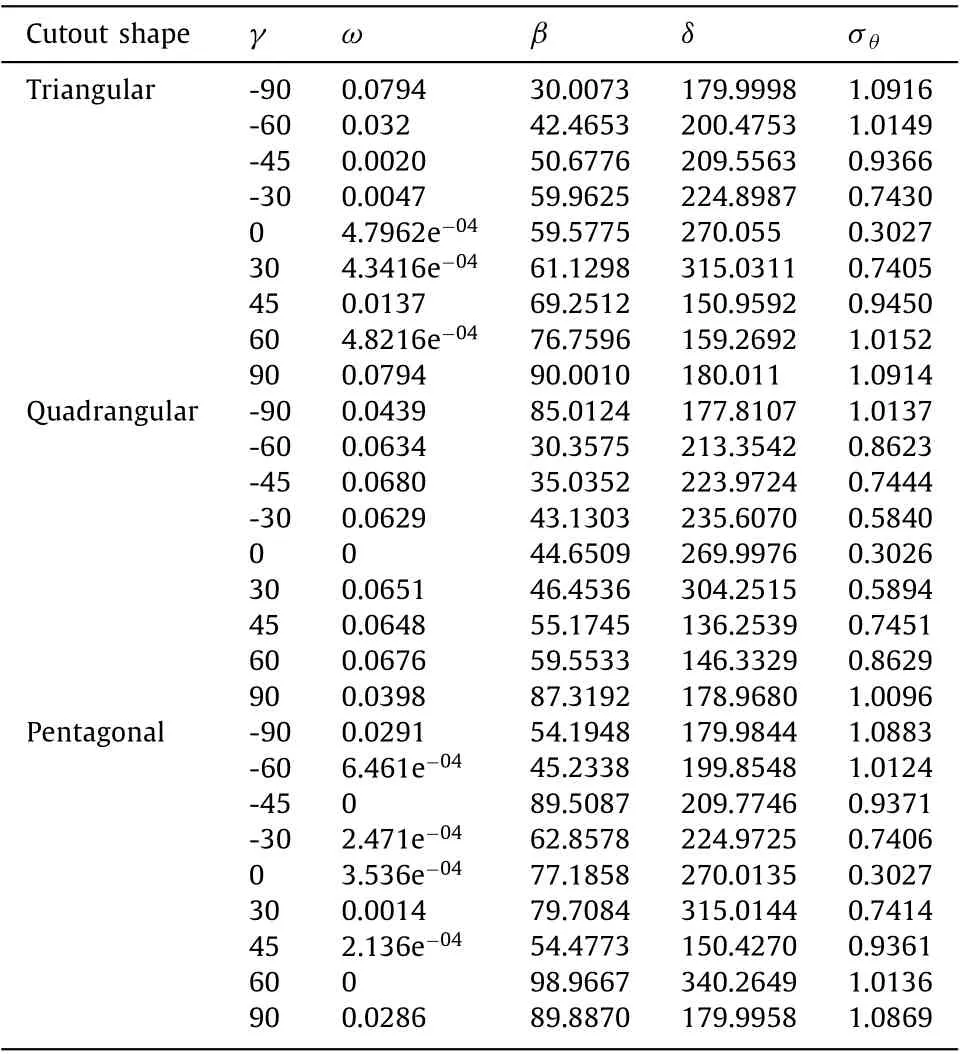
Table 6 Optimum values of design parameters and corresponding cost function in various fiber angles.

Table 6 shows the optimal values for the design parameters and the thermal stress amount at various fiber angles. The obtained values indicate that the optimal stress value for triangular, quadrilateral, and pentagonal openings occur atγ= 0 and equal to around 0.3026. As can be seen, the minimum stress in all three kinds of opening occurs in the circular form (ω= 0). The highest stress values for triangular and pentagonal openings occur atγ= -90 andγ= 90, which are very close to each other and equal to 1.0883 and 1.0916, respectively, so their diagrams are overlapped. However, the highest thermal stress is 1.0137 in quasi-square mode.

The convergence of the fibers’ angle in triangular, quadrilateral,and pentagonal openings is illustrated in Figs. 20 , 21 , and 22 , respectively.

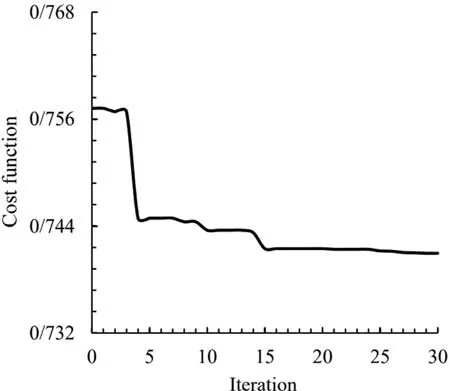
Fig. 20. Convergence of the objective function for triangular cutout.

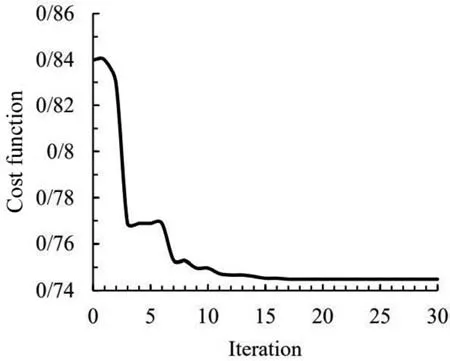
Fig. 21. Convergence of the objective function for quadrangular cutout.

One of the variables that affects the stress amount and distribution on the edge of the openings is the opening angle (β).The opening orientation is the rotation angle that the opening shape rotates compared to its original position. The effect of the opening rotation angle on the convergence of the optimal stress around triangular, quadrilateral, and pentagonal openings is shown in Table 7 . As can be seen, the optimal stresses for different values ofβare approximately the same and equal to 0.3026 in triangular and pentagonal openings. In both opening modes, the lowest value occurs in the circular state. This value for quadrilateral openings is the same and equal to 0.3103 for different values of the opening angle.

The convergence of the fibers angle for the triangular, quadrilateral, and pentagonal openings is illustrated in Figs. 23 , 24 , and 25 , respectively.

As can be seen, due to the optimization of the opening shape,especially in openings with an odd number of sides (deformation of the opening shape’s to circle), the effect of the opening orientation angle is not observed. Therefore, the effect of this parameter on a specific curvature (ω= 0.1) is investigated. Figure 26 shows that the optimal objective function behaves intermittently. Table 8 provides data for optimal design variables withω= 0.1 in different opening orientation angles. As shown in Fig. 26 and the data in Table 8 , the triangular and square diagrams have a higher frequency.

The heat flux angle is the angle that the heat flux vectors applied to the plate make with the horizon axis at infinity. The heat flux angle is one determining parameter in the stress distribution and its optimal values. As shown in Fig. 27 , for all opening shapes,the highest optimized stress occurs atδ= 0 andδ= 180, and the lowest optimal stress occurs atδ= 90. As can be seen in the figure, the diagrams of the triangular and pentagonal openings are almost overlapped.

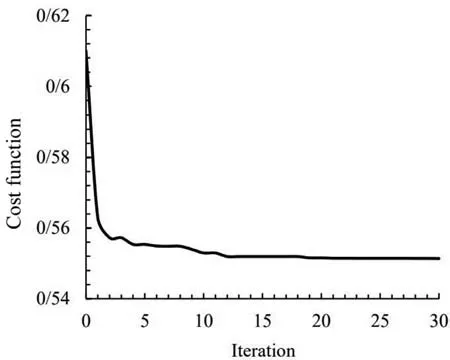
Fig. 22. Convergence of the objective function for pentagonal cutout.

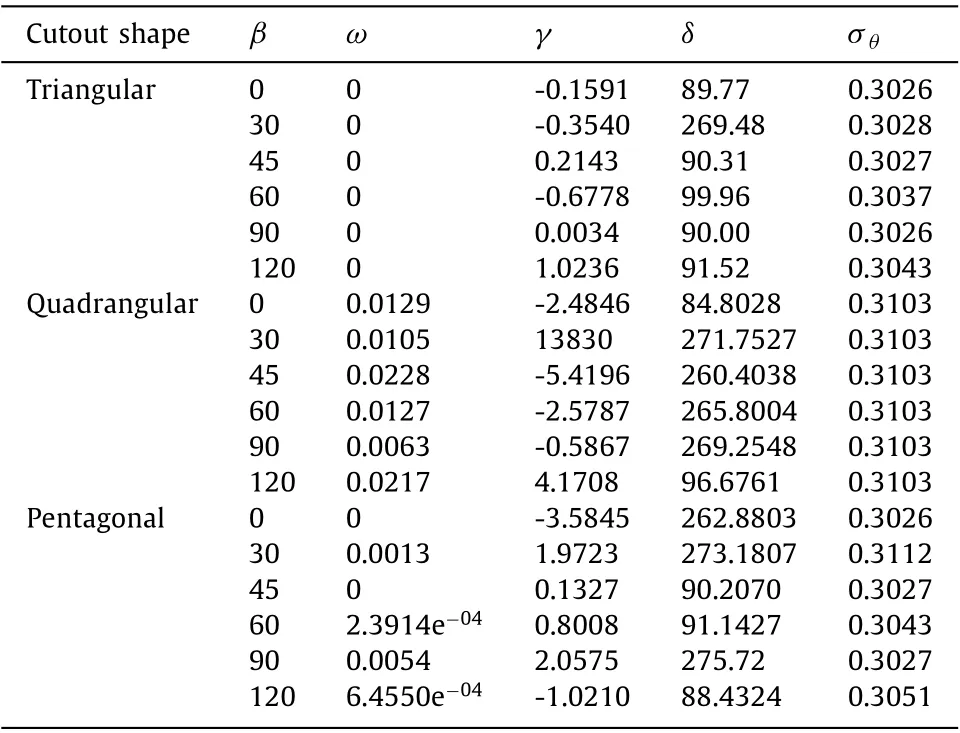
Table 7 Optimum values of design parameters and corresponding cost function in various hole angles.

As shown in Table 9 , the lowest optimal stress for all three shapes of openings occurs atδ= 90, equal to 0.3026, and the highest value occurs atδ= 0 andδ= 180. As for the heat flux angle, like the previous three parameters, the optimal opening geometry for the triangle and the pentagon isω= 0 (circular cutout), but for the quadrilateral, the optimal corners’ curvature is non-zero.

Heat flux convergence for triangular, quadrilateral, and pentagonal openings can be seen in Figs. 28 , 29 , and 30 respectively.

Thecombination effect of all design variables on the stress concentration for different openings is investigated. These parameters include opening corners’ curvature, fiber angle, opening orientation, and heat flux angle. Table 10 shows the optimal values of the design parameters and the corresponding optimal objective function for the openings examined in this paper.

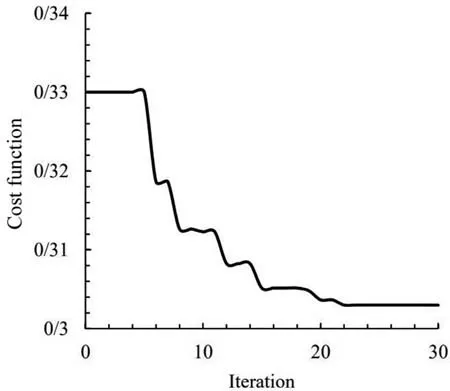
Fig. 23. Convergence of the objective function for triangluar cutout.

Fig. 24. Convergence of the objective function for quadrangular cutout.

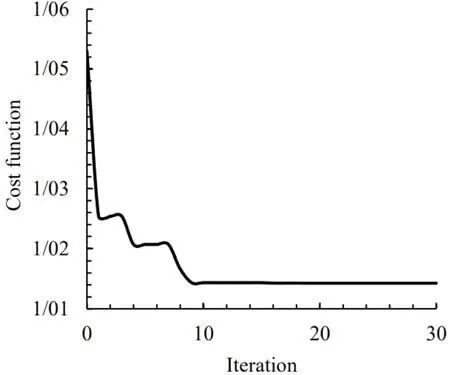
Fig. 25. Convergence of the objective function for pentagonal cutout.

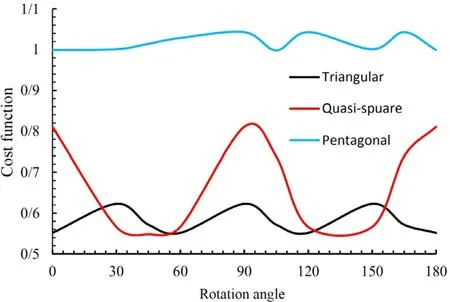
Fig. 26. Effect of opening rotation angle on optimum value of cost function for various shapes of cutout with ω= 0.1.

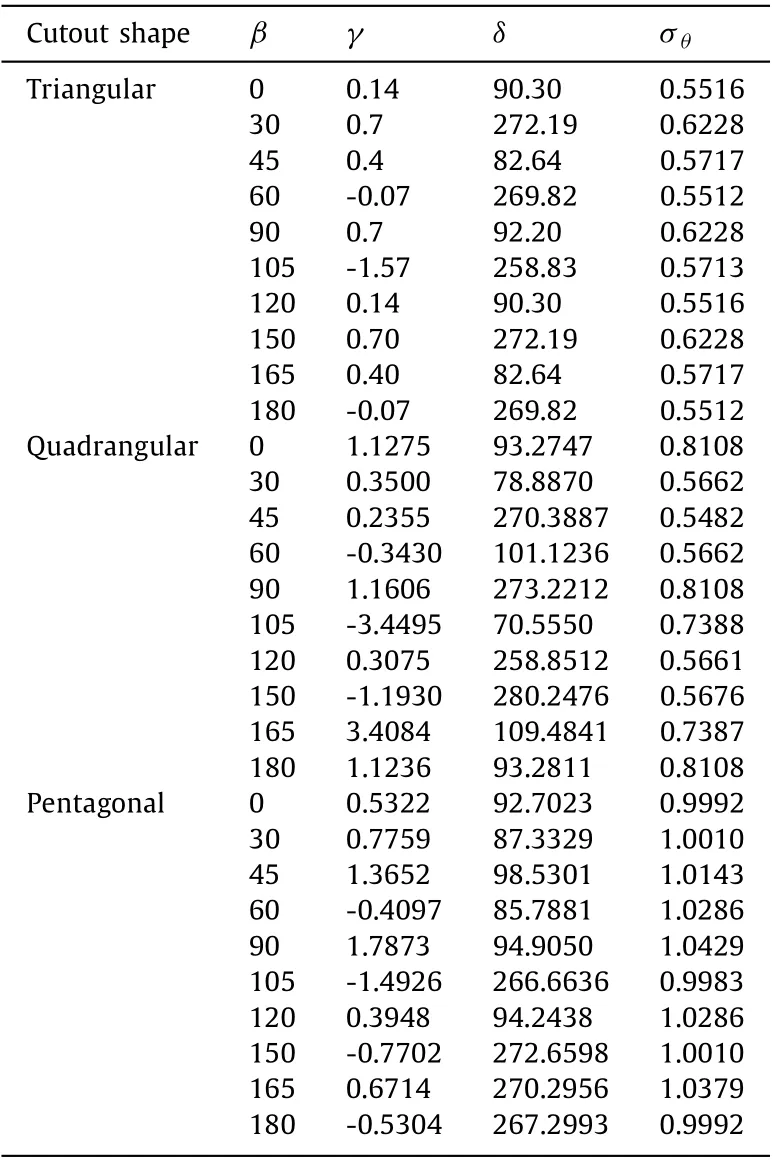
Table 8 Optimum values of design parameters and corresponding cost function for various hole angles with ω = 0.1.

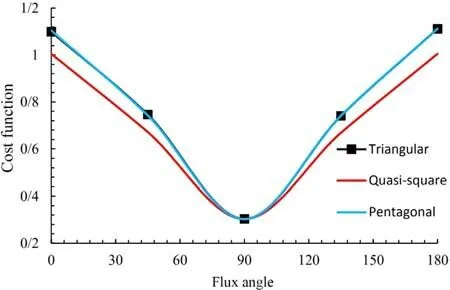
Fig. 27. Effect of heat flux angle on optimum value of cost function in various shapes of cutout.

Table 9 Optimum values of design parameters and corresponding cost function for various heat flux angles.

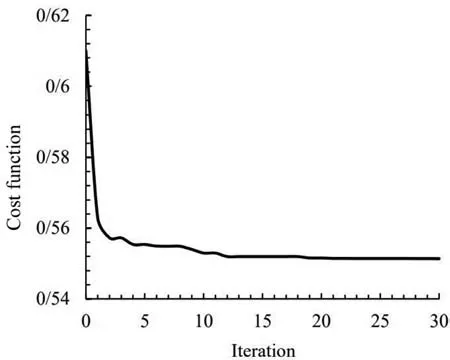
Fig. 28. Convergence of the objective function for triangluar cutout.

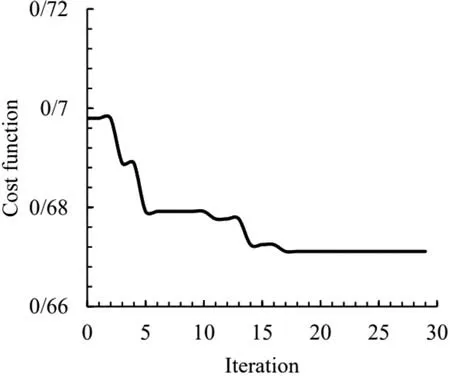
Fig. 29. Convergence of the objective function for quadrangular cutout.

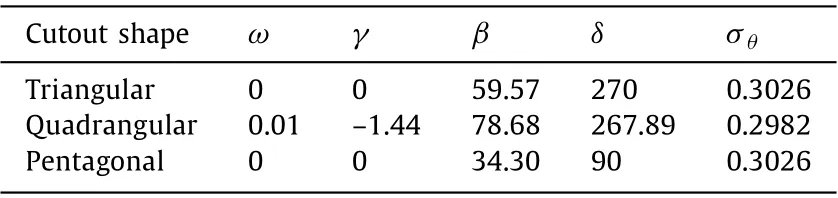
Table 10 Optimal values of design parameters.

Fig. 30. Convergence of the objective function for pentagonal cutout.

In this research, with the help of an analytical solution based on Lekhntiskii’s complex variable method and using a conformal mapping function, stress concentration was optimized in anisotropic single-layer plates containing openings with different shapes using the genetic algorithm. In this study, it was well shown that several parameters affect stress concentration. These parameters include opening corners’ curvature, fibers angle, opening rotation angle, and heat flux angle. By selecting these parameters correctly,the lowest possible stress concentration around the opening can be achieved. For this purpose, the effect of all parameters together for openings with different shapes was investigated and introduced.The results showed that for openings with an odd number of sides,the optimal stress concentration occurs in the opening curvature of zero (circular opening), while for openings with an even number of sides, optimum corners curvature is non-zero. The results and implemented methodology in this study can be utilized to find the amount and location of the maximum thermal stress around cutouts and introduce the optimal design for perforated anisotropic and isotropic plates to achieve structural integrity and prevent failure.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.