Importance of induced magnetic field and exponential heat source on convective flow of Casson fluid in a micro-channel via AGM
2022-08-26HsiiGholmiAsdiGnji
A. Hsii , A. Gholmi , Z. Asdi , D.D. Gnji ,*
a Department of Mechanical Engineering, Babol University of Technology, P.O. Box 484, Babol, Iran b Department of Mechanical Engineering, Islamic Azad University, Sari, Iran
Keywords:AGM method Casson fluid Microchannel Exponential heat source
ABSTRACT The study of the natural convective flow of a fluid in the presence of an induced magnetic field has always been of considerable importance due to its many applications in various areas of science, technology, and industry, such as the operation of magnetohydrodynamic generators. This study addresses an analysis of exponential heat source and induced magnetic field on the second-class convection of Casson fluid in a microchannel. The flow is in a vertical microchannel organized by two vertical plates. The answer to governing equations has been grabbed for temperature field, induced magnetic field, and velocity via Akbari-Ganji’s method (AGM). Nusselt number, skin friction coefficient, and current density are approximated. Graphs that describe the conclusion of influential physical variables on velocity, temperature,current density, induced magnetic field, and skin friction coefficient distributions are shown. Comparison of results with numerical method (Runge-Kutta-Fehlberg, RKF-45), homotopy perturbation method, and AGM confirms the accuracy of answers obtained with AGM.
High thermal performance is always essential to thermal systems, and finding new ways to increase heat transfer rate (HTR) in thermal systems has attracted the attention of many researchers.A heat exchanger is a device for transferring energy between two objects with a temperature difference. Heat exchangers may be found in automotive air conditioners, petroleum/chemical processing, pharmaceuticals. Tuckerman and Pease [1] used a microchannel as a heat exchanger for the first time. The results show that the use of channels with a high aspect ratio leads to decreased thermal resistance. The heat transfer between two various liquids in a microchannel was first investigated by swift [2] . The heat transfer between propylene and water in a heat exchanger is measured based on the fluid properties and geometry of the exchanger. Chen and Weng [3] studied natural convection (NC) in an open-ended microchannel. The results showed that dilution, fluid-wall interplay, and slip-flow NC have considerable efficacies on the studied flow. Later, Jha et al. [4] found that HTR andτstrongly depend on the injection/suction parameter. Wang and Chiu-On [5] studied NC under a no-slip condition in a microchannel. All these studies show that by accounting for the microchannel, heat transfer can be increased. In the above studies related to NC, the linear Boussinesq approximation has been used. Due to the direct relationship between density and increasing temperature difference, nonlinear vibration in density may affect the flow. Vajravelu et al. [6] suggested the nonlinear density change with temperature, and the corresponding equation is as follows:


The results are obtained using the schauder theory. Further, although Mahantesh et al. [7] numerically investigated the effects of nonlinear radiation and convection in a non-Newtonian nanofluid.The results show that the temperature profile in the solar radiation case is stronger than the case without radiation. Hayat et al.[8] investigated the nonlinear convection flow of magnetohydrodynamics (MHD) in a nanofluid. The results show that the qualitative behaviors of thermal layer thickness and temperature are similar for the temperature- ratio and radiation variables. Waqas et al. [9] , and many others have done studies on nonlinear convection, the literature on it using microchannels is restricted. With the introduction of non-Newtonian theory, it became possible to describe the properties of various materials, such as printing inks,and paint. For the first time, Casson introduced the Casson fluid(CF) model to describe viscoelastic fluids and had features such as high shear viscosity. Casson fluid has many applications in metallurgy, and petrochemicals. Tamoor et al. [10] investigated the flow of CF on a stretching cylinder using a magnetism. The results show that when the fluid’s viscosity is variable, the heat transfer rate is higher. Shashikumar et al. [11] investigated the Magnetohydrodynamics flow of CF using a porous microchannel exposed to thermal radiation. The results show that the heat field and velocity change inversely for the larger Hartmann number. Makinde et al. [12–13] investigated the blended impact of suction/injection, thermal radiation, magnetic field, and porous media in the forced convection flow in a vertical and horizontal microchannel with temperature jump conditions and velocity slip. The results show that fluid velocity and heat transfer rate increase due to Dufour and Soret numbers. Also, increasing the Biot number leads to an increase in the entropy generation rate. Basant et al. [14] Reviewed the importance ofHby NC in a vertical microchannel. The results show that the entropy generation rate is strongly influenced by the caisson fluid parameter and the magnetic field. Shivakumar et al. [15] investigated the impact ofHon the forced convection exposed to the magnetic field. The results show that the entropy generation rate is improved in the presence of a magnetic field with a suitable combination of thermophysical parameters. Jha et al. [16] investigated the natural convective flow of MHD in a vertical microchannel with electrically nonconductive walls. Kunnegowda et al. [17] investigated the importance ofQandHon second-class convection flow in a microchannel in the presence of CF. The governing equations are solved by the HPM method. Hosseinzadeh et al. [18] Investigated the flow of non-Newtonian blood fluid containing nanoparticles inside a porous vessel, and the governing equations were solved by the Akbari-Ganji’s method (AGM). Ramudu et al. [19] investigated the effect of MHD Casson fluid on a convective surface with chemical reaction, cross-diffusion, and nonlinear radiant heat.The results show that increasing the Soret number increases the concentration and decreases the temperature. Samrat et al. [20] investigated the buoyancy effect on the MHD radiative flow of Casson fluid by considering thermophoresis and Brownian moment.The results show that the impact of the Brownian moment on the non-Newtonian flow is more significant. Samrat et al. [21] studied the heat transfer of MHD Casson, Williamson, and Carreau fluids on a parabolic surface in the presence of an exponential heat source. The results show that the Casson fluid’s thermal conductivity is higher than the other two fluids. Kumar et al. [22] investigated the heat transfer of non-Newtonian MHD fluid on a melting surface in the presence of an exponential heat source. The results show that the melting parameter has a decreasing effect on all flow fields. Mahanthesh [23] numerically investigated the heat transfer of a nanofluid in the presence of aggregation kinematics of nanoparticles and quadratic radiative heat flux. The results show that the suspension of particulate matter leads to increased thermal conductivity and temperature. Mahanthesh et al.[24] statistically investigated the effect of exponential heat source on Williamson nanofluid heat transfer using nonlinear Boussinesq approximation. The results show that increasing the Biot number increases concentration and temperature. Reddy et al. [25] investigated the generation of tangent hyperbolic fluid entropy in a vertical microchannel using the Boussinesq approximation. The results show that the buoyancy force and the Eckert number lead to an increase in entropy. Al-Kouz et al. [26] have studied quadratic convection and thermal radiation on the viscoelastic flow in the presence of a heat source. The results show that quadratic convection leads to an increase in the Nusselt number.
Because the speed and accuracy of solving equations are always of particular importance, the AGM method allows accurate results obtained at a lower computational cost. Therefore, this study solves the governing equations using the AGM method [27] and compares it with the numerical method (Runge-Kutta-Fehlberg, RKF-45) and homotopy perturbation method (HPM), under temperature jump conditions and velocity slip. The results confirm the speed and accuracy of the AGM method.
Consider two infinite vertical planes is as presented in Fig. 1.The second-class convection flow with an exponential heat source in the presence of CF is assumed in a vertical microchannel. Flow is considered to be unidirectional and non-transient. In the assumed coordinate axis, thex’ -axis is considered opposite to the direction of gravity and they’ -axis is considered perpendicular to the plates.The plates are heated asymmetrically, with the left and right plates maintained atT1 andT2 , respectively (T1>T2 ). As a result, nonlinear convection occurs due to the vast temperature difference between the two plates in the microchannel.
Based on these hypotheses, the governing equations of the magnetic field, energy, and motion are as follows ( [14] ):
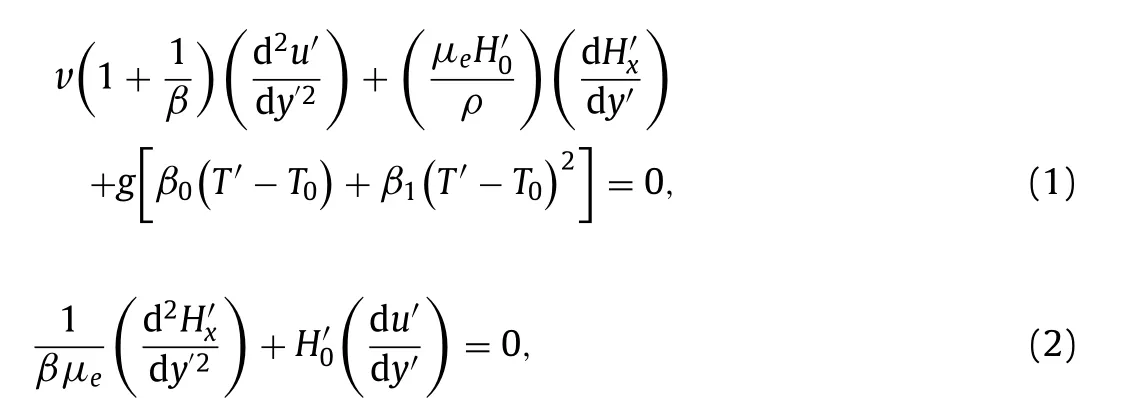

Fig. 1. The physical adjustment of the microchannel.

According to the coupled system of nonlinear differential equations explained earlier, boundary conditions due to the fundamental idea of the AGM [28] , Eqs. (1) –(5) have been rewritten in the following order:
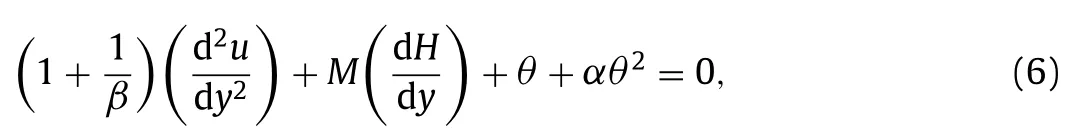
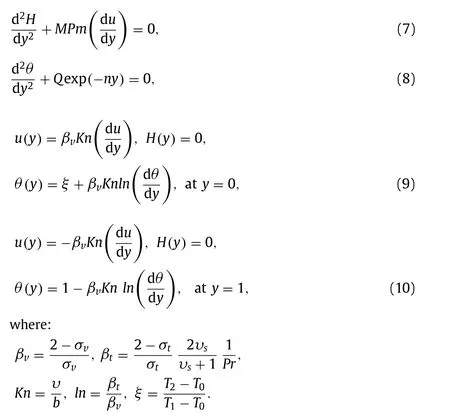
According to the fundamental idea of AGM, a suitable test function has been studied as the solution of the supposed differential equation.it is considered a finite polynomial series with constant coefficients, as follows:
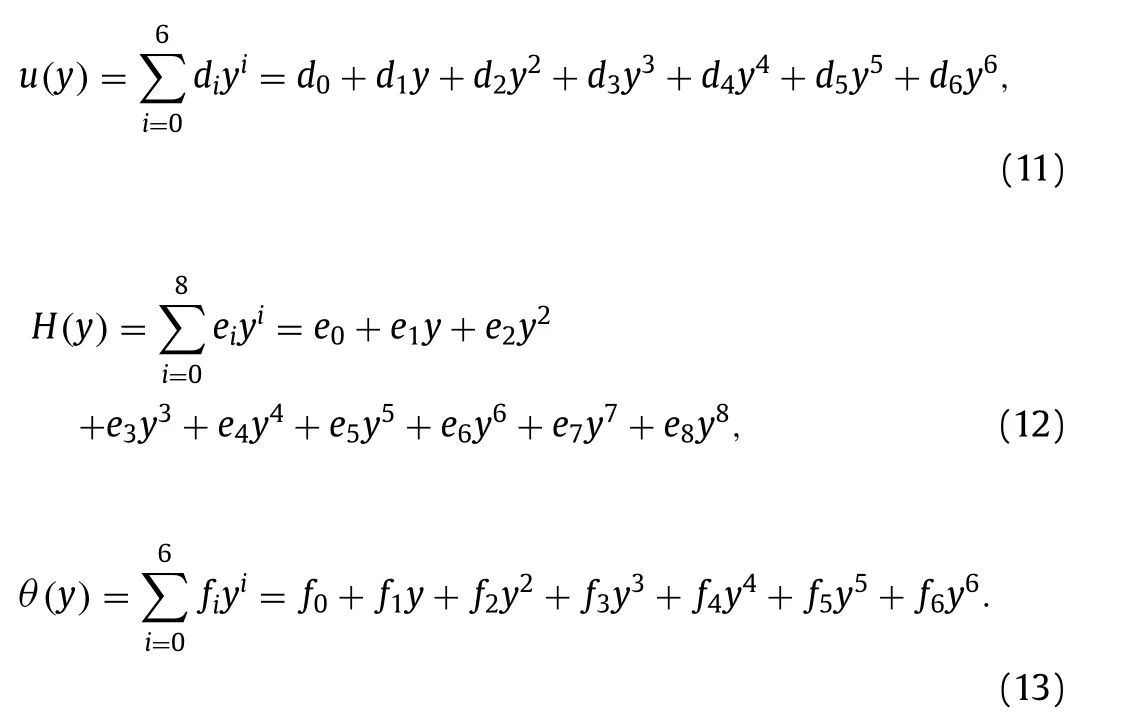
To accredit the precision of the solution reached by AGM method
As can be seen in Tables 1 and 2, the AGM method has good accuracy compared to the reproducing kernel finite-volume method(RKFM), and the results obtained are entirely consistent with previous studies.
The primary target of this segment is to investigate the impact ofQ,Pm,M,α,β,βvkn,n, andlnonu(y),H(y),θ(y),J(y),τ,Qm,andNuprofiles under three cases ofξ(ξ= 1 for symmetrical heating,ξ= 0 for one heating and one not heating,ξ= -1 for one cooling and one heating). The provided investigation has been carried out in the slips and continuum flow regimes (kn≤0.1).Via the numerical calculation the other parameters are chosen asM= 5,Pm=α=β=n= 0.5,βvkn= 0.05,ln= 1.667 andQ= 2.Figure 2 a and 2 b represent the impact ofξandQon (y) and (y)whenM= 5,Pm=β=α=n= 0.5,βvkn= 0.05 andln= 1.667.HereQandξraise with increasing (y) and (y), this is due to the portion of more heat into the system under review so that the heat has been attracted by fluid particles and therefore have an orientation to move faster. as well as seen that there is a junction point inside the microchannel which causes theH(y) to be autonomous ofQ.
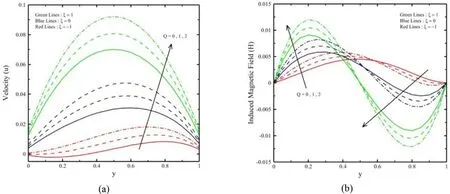
Fig. 2. ( y ) and ( y ) for various Q.
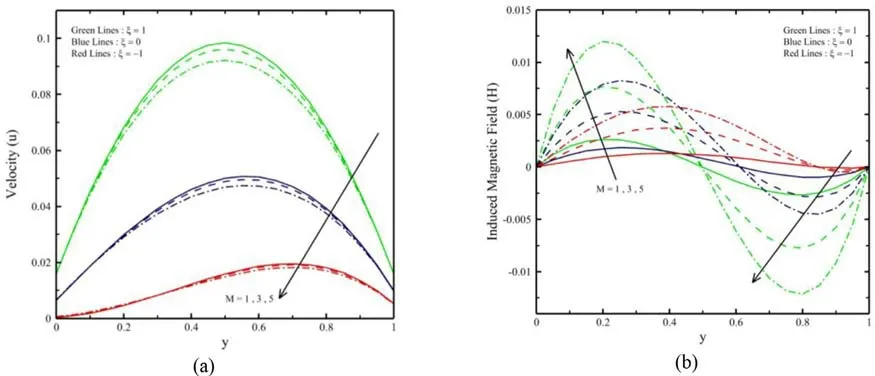
Fig. 3. ( y ) and ( y ) for various M.
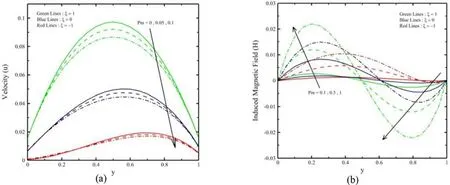
Fig. 4. ( y ) and ( y ) for various P m .

Fig. 5. ( y ) and ( y ) for various β.
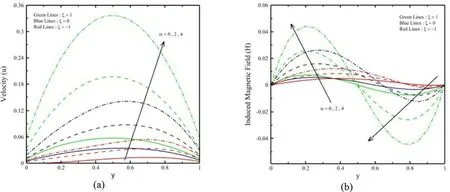
Fig. 6. ( y ) and ( y ) for various α.
Figures 3 a and 4 a represent the efficacy ofMandPm, respectively on (y). HerePmandMraise with reducing (y) and (y) due to the attendance of Lorentz force, which is a contrary force on the velocity field. Also seen when heating is asymmetric (ξ= -1),there is a junction point inside the microchannel, while the velocity field is autonomous ofMandPm. The effect ofPmandMon the microchannel slip velocity becomes considerable asξraises.Figures 3 b and 4 b represents the change ofMandPmon H, respectively. It is observed that close to the microchannel wall aty= 0.the induced magnetic field is straightly commensurate toPmandMwhile the reverse orientation is noticed close to the microchannel wall aty= 1. further, inside the vertical microchannel, there is a junction point which causes theH(y) to be autonomous ofPmandM. The impact ofPmandMon the microchannel slip velocity becomes considerable asξraises. Figures 5 and 6 represent the impact ofβandαon (y) and (y), respectively. It is observed that an increment inαcauses an increment in the velocity profile due to powerful buoyancy force. The velocity rises withβlead to the reduction in the yield stress. The increment inαand CF increasesHclose to the microchannel wall aty= 0. At the same time, the inverse character is noticed aty= 1. Further,Hbecomes autonomous ofβandαbecause of the existing junction point inside the vertical microchannel. Figures 7 a and 8 a represent the impacts ofβvknandlnon (y). An increment inβvkn,lnandξleads to an increment in the slip of fluid, and the fluid velocity rises. Here is the fluid velocity raises with increment inln. Also, the impact ofβvknand on the velocity becomes considerable asξraises. Figures 7 b and 8 b represent the impact ofβvknandlnon (y). It is noticed that (y) rises with increment inβvkn,lnandξ.
Figures 9 and 10 illustrate the impact ofnandQon (y) and(y) and. It is noticed that the temperature profile is enhanced by raising the value of the heat source parameter due to the waste of energy. In contrast, the decrease in the temperature profile was observed by raising the value ofn. A similar nature observed inJ.Figures 11 a and 12 a show the impact ofβvknvknandlnon (y).It is illustrated that an increment inβvknandlnleads to raises in the temperature profile due to the increment in the temperature jump. The effect ofβvknandlnon (y) becomes considerable asξraises. Figures 11 b and 12 b represents the impact ofβvknandlnon (y). It is noticed that an increment in bothβvknandlnleads to increases in (y) in the regiony∈ (0.2, 0.7) while the reverse orientation is observed in the regiony∈ (0, 0.2) andy∈ (0.7, 1).Forξ, the reverse impact ofJis observed. It is noticed that theJbecomes autonomous of ln andβvknat two points because of the presence of junction points inside the microchannel..
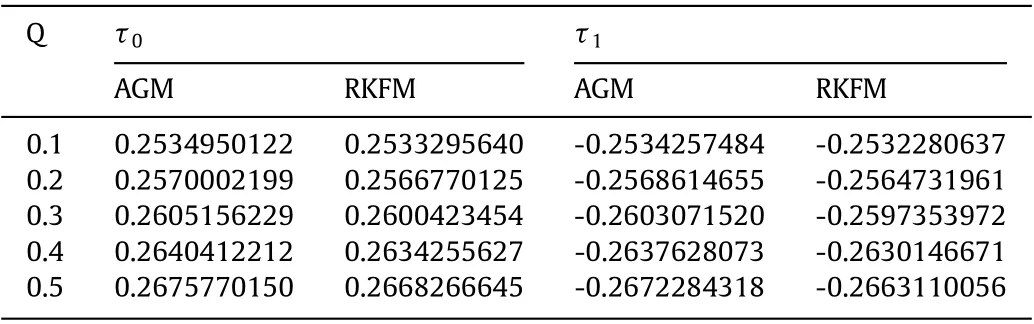
Table 1 Comparison of AGM and RKF-45 method solution for τ0 and τ1 when P m = β = n = α = 0.5, ln = 1.667, M = 5 and ξ = 1
The numerical (RKF-45) values ofQmfor variousM,Pm,β,n,andlnwhenQ= 2 andα= 0.5 are given forξ= 1 andξ= 0 in Table 3 . the linear regression gradient using data points is approx-
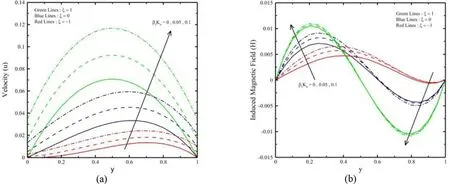
Fig. 7. ( y ) and ( y ) for various βv k n .

Fig. 8. ( y ) and ( y ) for various ln.
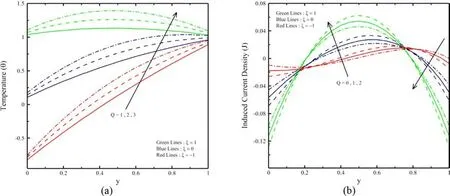
Fig. 9. ( y ) and ( y ) for various Q.
imated to know the value of decrease or increase in theQm. It is observed that theQmis a declining function ofPm,M, andnwhileQmis a rising function ofβandln. Effect ofβonQmis more considerable than that ofln. Tables 4 and 5 show the numerical values of t aty= 0 andy= 1 respectively for variousM,Pm,β,n, andlnwhenQ= 2 andα= 0.5. It is seen that theτ0is a rising function ofPm,M,β,n, andln. Effect ofnonτ0is rather considerable than that ofPm,M,β, andln. Table 4 shows thatτ1is a rising function ofPm,M, andnwhile it is a declining function ofβandln.
In the present paper, the importance ofQandHon second-class convection flow in a microchannel in the presence of CF under velocity slip and temperature jump conditions are studied analytically using AGM. The results are as follows.:
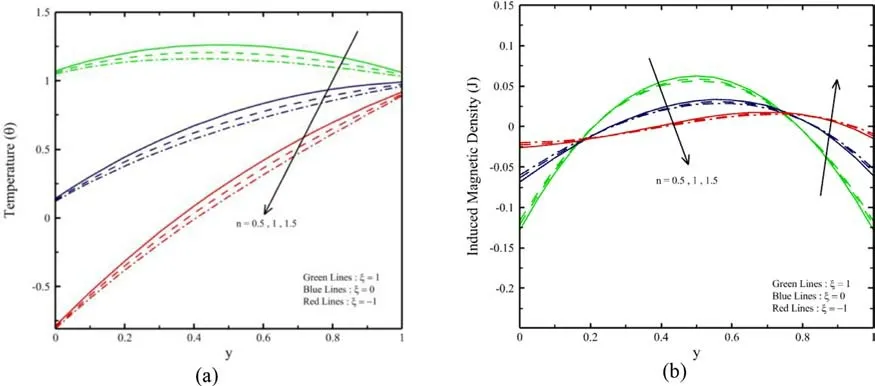
Fig. 10. ( y ) and ( y ) for various n.
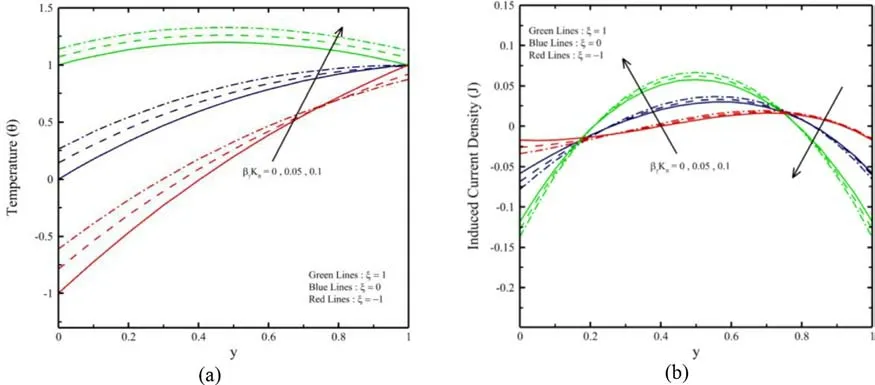
Fig. 11. ( y ) and ( y ) for various βv k n .

Table 2 Comparison of AGM and RKF-45 method solution for Nu 0 and Nu 1 when P m = β = n = α = 0.5, ln = 1.667, M = 5 and ξ = 1
(1) A junction point in the H profile inside the vertical microchannel makes the H autonomous of the parameters involved.
(2) There are two junction points inside the vertical microchannel forJ.
(3) The impact ofPmandMon velocity profile leads to a junction point when heating is asymmetric (ξ= -1) inside the microchannel.
(4) The nonlinear convection parameter is desirable for (τ0).
(5) Effect ofQand CF parameters is accepted for all flow fields in terms of quality.
(6) The Nusselt number is less when heating is symmetric in comparison with asymmetric heating.
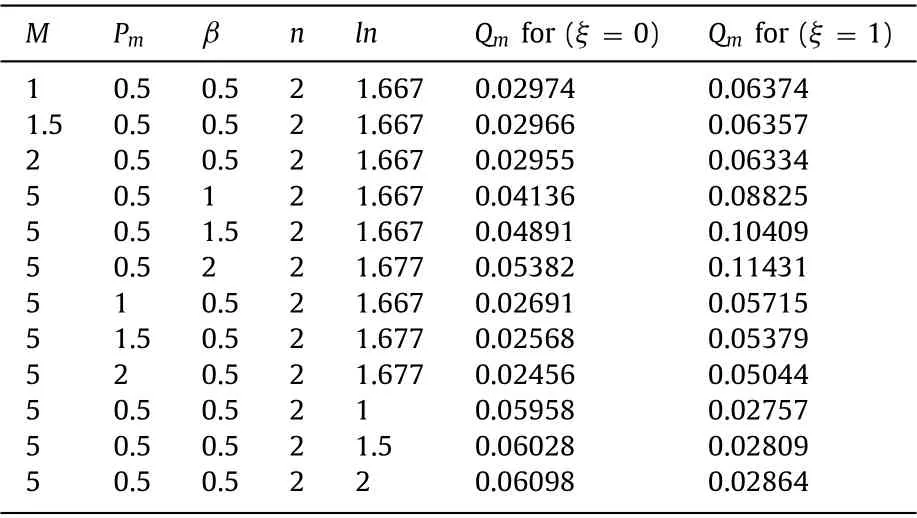
Table 3 Numerical (RKF-45) values of Q m for various M, P m , β, n, ln when Q = 2,βv k n = 0.05 and α = 0.5
(7) The effect of Pm and M on the microchannel slip velocity becomes significant asξraises.
(8) The temperature profile is improved by growing the value of the heat source parameter due to the destruction of energy.
(9) The Impact ofnonτ0 is moderately more notable than that ofPm,M,β, andln.
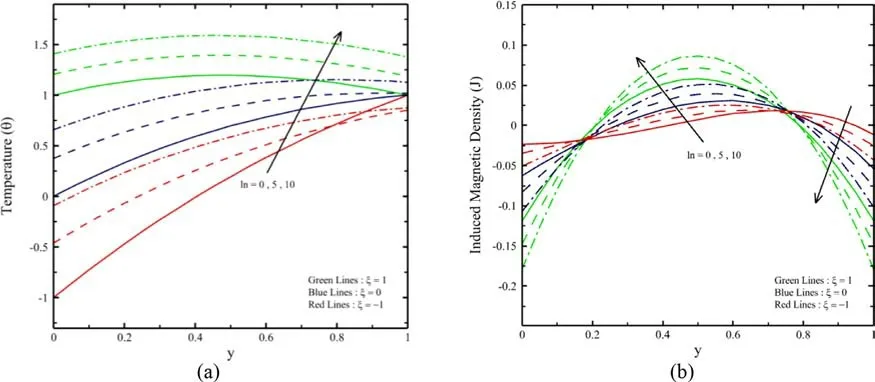
Fig. 12. ( y ) and ( y ) for various ln.
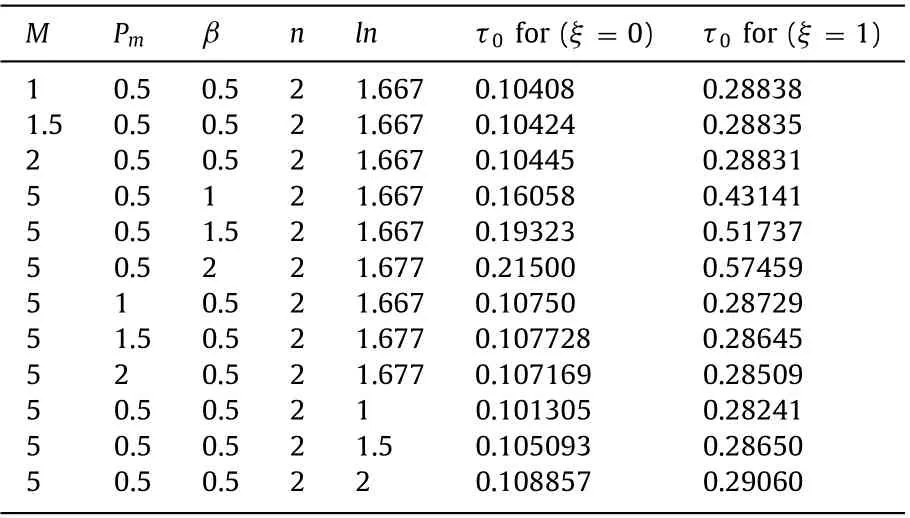
Table 4 Numerical (RKF-45) values of τ0 for various M, P m , β, n, ln when Q = 2,α = 0.5
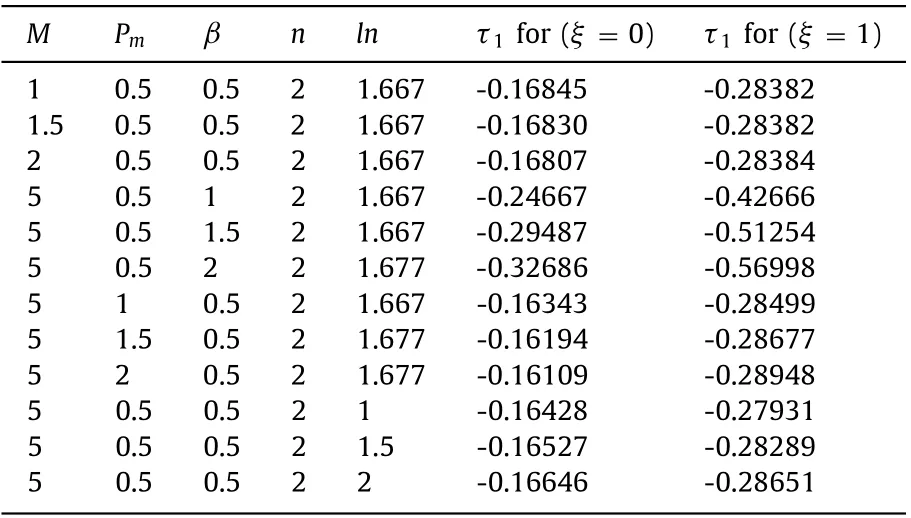
Table 5 Numerical (RKF-45) values of τ1 for various M, P m , β, n, ln when Q = 2,α = 0.5
Declaration of Competing Interest
The authors declares that there is no conflict of interests regarding the publication of this paper.
杂志排行
Theoretical & Applied Mechanics Letters的其它文章
- Useful zero friction simulations for assessing MBS codes Pascal’s formula giving wheelsets frequency for zero wheel-rail friction
- Optimal thermal design of anisotropic plates with arbitrary cutouts using genetic algorithm
- Optimal patching locations and orientations for maximum energy harvesting efficiency of ultrathin flexible piezoelectric devices mounted on heart surface
- Similarity solutions of Prandtl mixing length modelled two dimensional turbulent boundary layer equations
- Numerical simulation of droplet coalescence based on the SPH method
- Thermal energy storage inside the chamber with a brick wall using the phase change process of paraffinic materials: A numerical simulation
