Thermal energy storage inside the chamber with a brick wall using the phase change process of paraffinic materials: A numerical simulation

M. Jvidn , , M. Asgri , M. Gholini , , M. Nozri b , A. Asgri c , D.D. Gnji ,

a Department of Mechanical Engineering, Babol Noshirvani University of Technology, Babol, Iran

b Department of Chemistry, Drexel University, Philadelphia, USA

c Department of Mechanical Engineering, Shiraz University, Shiraz, Iran

Keywords:Thermal energy storage Heat transfer fluid Radiation heat transfer Phase change material

ABSTRACT Phase change materials are one of the potential resources to replace fossil fuels in regards of supplying the energy of buildings. Basically, these materials absorb or release heat energy with the help of their latent heat. Phase change materials have low thermal conductivity and this makes it possible to use the physical properties of these materials in the tropical regions where the solar radiation is more direct and concentrated over a smaller area. In this theoretical work, an attempt has been made to study the melting process of these materials by applying constant heat flux and temperature. It was found that by increasing the thickness of phase change materials’ layers, due to the melting, more thermal energy is stored. Simultaneously it reduces the penetration of excessive heat into the chamber, so that by increasing the thickness of paraffin materials up to 20 mm, the rate of temperature reduction reaches more than 18%. It was also recognized that increasing the values of constant input heat flux increases buoyancy effects. Increasing the Stefan number from 0.1 to 0.3, increases the temperature by 6%.

From the past to the present, many energy sources have been utilized to meet human needs, but many of them such as fossil fuels are greatly harmful to the environment. Devastating impact of carbon pollutants and greenhouse gases emitted to the atmosphere are just some of these adverse effects. Recently, new energy research has focused on improving energy efficiency and researchers have conducted numerous studies to discover new and efficient energy sources [1–3] . Considering production costs and efficiency, new sources such as geothermal energy, wind energy, and solar energy have been introduced which are economically viable[4–5] . But the approach here is to be able to store energy for a longer period of time in order to be utilized when needed. By using phase change materials (PCMs) it is possible to store or release energy. Based on their latent energy of melting and freezing, PCMs are able to absorb a large amount of energy from the surrounding environment and release it when necessary [6–8] . One of the advantages of using these materials for energy storage is that they are not destructive, they can be used during phase changing cycles, and they also have suitable chemical properties. Due to the variety of PCMs, they can be used in various fields such as electrical appliances, solar panels, thermal protection of certain drugs,and heat exchangers [9–11] . In the following section, some of scientific works in the field of thermal energy will be introduced. Al-Abidi et al. [12] studied the latent heat storage of PCMs in a heat exchanger through simulation work. Their main approach was to analyze the melting process. They found that by adding conductive nanomaterials, the thermal conductivity of PCMs would increase and ultimately the process completion time would be reduced. Pizzolato et al. [13] investigated the effects of heat transfer and melting of PCMs by simulating the installation of conductive fins on heat exchangers containing PCMs. In this simulation, they tried to use the Topology-Optimization to optimize the dimensions of fins to increase heat transfer. Nakhchi et al. [14] simulated the melting process of PCMs enclosed in a rectangular chamber. In this computational work, they evaluated the acceleration of the melting process of PCMs by examining various shapes of fins. They found that by using sloped fins the melting process time could be reduced. Mehdi et al. [15] investigated the behavior of PCMs during the melting process affected by convective heat transfer. In this numerical work, they tried to improve the heat transfer rate by using conductive nanoparticles and copper fins. Their results showed that the use of fins installed in the lower half of the heat exchanger plays a more effective role in increasing the heat transfer rate. In an analytical study, Gholinia et al. [16] explored the effects of employing conductive particles in the form of hybridized carbon nanotubes under magnetic effects. Their results showed that although increasing the concentration of nanoparticles leads to increased heat transfer, the flow rate of fluid inside the chamber reduces.Hatami et al. [17] analyzed the effects of convective heat transfer in a chamber with wavy geometry by a mathematical study.They examined the interaction between the effects of buoyancy and viscosity by adding nanoparticles and making changes in the physical properties of the fluid in the chamber. In another study,Rahman et al. [18] investigated the effects of heat penetration and heat transfer under magnetic fields. They stated that by increasing inertia parameters, the temperature gradient decreases. Asgari et al. [19] explored the solidification process of PCMs in a heat exchanger by a computer simulation. The main approach was to investigate the enthalpy of PCMs during changing state. They tried to increase the heat transfer rate by installing branch-shaped fins on the heat exchanger. They also tried to increase the thermal conductivity of PCMs by adding different amounts of nanoparticles.Their results showed that using long fins leads to improved process speed. Lohrasbi et al. [20] studied the storage of thermal energy by employing PCMs in the heat exchanger. In this simulation, they relied on passive techniques to study melting and solidification of materials. They found that using thinner and longer fins causes the materials to change phase over a shorter period of time. Rahman et al. [21] investigated the effects of convection on fluid heat transfer in a trapezoidal chamber. They stated that increasing Reynolds values leads to increased heat transfer and uniformity in temperature distribution. Hatami and Ganji [22] studied heat transfer in a heat sink through an analytical study. In this work, they solved complex nonlinear equations using the LSM method. They found that increasing the diameter of the copper nanoparticles added to the fluid, rises the heat transfer rate. Several other researchers have also studied the energy storage of PCMs in heat exchangers [23–25] . Mottahar [26] simulated the melting process of PCMs under constant heat flux in a chamber. In this work, it was shown that increasing the heat flux leads to an increase in the Nusselt value.In an experimental and numerical study, Bouhal et al. [27] investigated the thermal performance of PCMs for storing thermal energy in a building. In this work, they simulated melting and freezing process of paraffinic materials inside a rectangular cubic chamber.They concluded that increasing the heat capacity leads to more heat absorption.

In this simulation, the effects of melting temperature of PCMs on the internal temperature of the chamber were evaluated. Then the effects of specific heat capacity on heat absorption and temperature tension of PCMs were investigated. The heat transfer for two paraffinic organic PCMs RT21, RT26 during the melting process has been investigated and compared. It should be noted that the effects of changing PCMs’ layers under constant flux were also studied and simulated in order to obtain a better evaluation of heat transfer and storage of thermal energy. Another issue to be considered is to investigate heat distribution and phase change of the material inside a cavity with transparent coating which is directly exposed to heat radiation. It is worth noting that the research on the use of bricks and PCMs RT21 and RT26 against the heat source and radiation load has not been addressed in the literature, so this paper tries to eliminate this research gap with the help of numerical simulation.

In this work, the thermal energy storage of paraffin PCMs during the melting process has been studied using the passive technique. In this simulation, using the energy enthalpy, the amount of energy released during the phase change of PCMs has been investigated. This study is two-dimensional with constant heat flux applied to the chamber containing PCMs. The radiation effect has also been studied by examining the opacity and transparency of the chamber. It is worth mentioning that the problem was transient, and simulation was performed using the ANSYS-Fluent software. The initial temperature in this simulation was 295.15 K and the hot wall of the chamber was subjected to heat fluxes of 150,200 and 250 ( A.W / m2). The assumed conditions are as follows:

(1) Viscous loss is negligible.

(2) Using the Boussinesq approximation, the buoyancy effects are noticeable.

(3) No-slip condition at the walls is satisfied.

In this simulation, PCMs are placed inside aluminum chambers.These chambers are also embedded in a wall subjected to the heat of a brick room. The walls of this room are considered completely insulated except the only wall containing PCMs through which the heat can penetrate into the chamber (See Fig. 1 ).

Since the volume of PCMs changes slightly during the phase change, the mathematical model can be derived by continuity, momentum and energy equations [14] :

The continuity equation

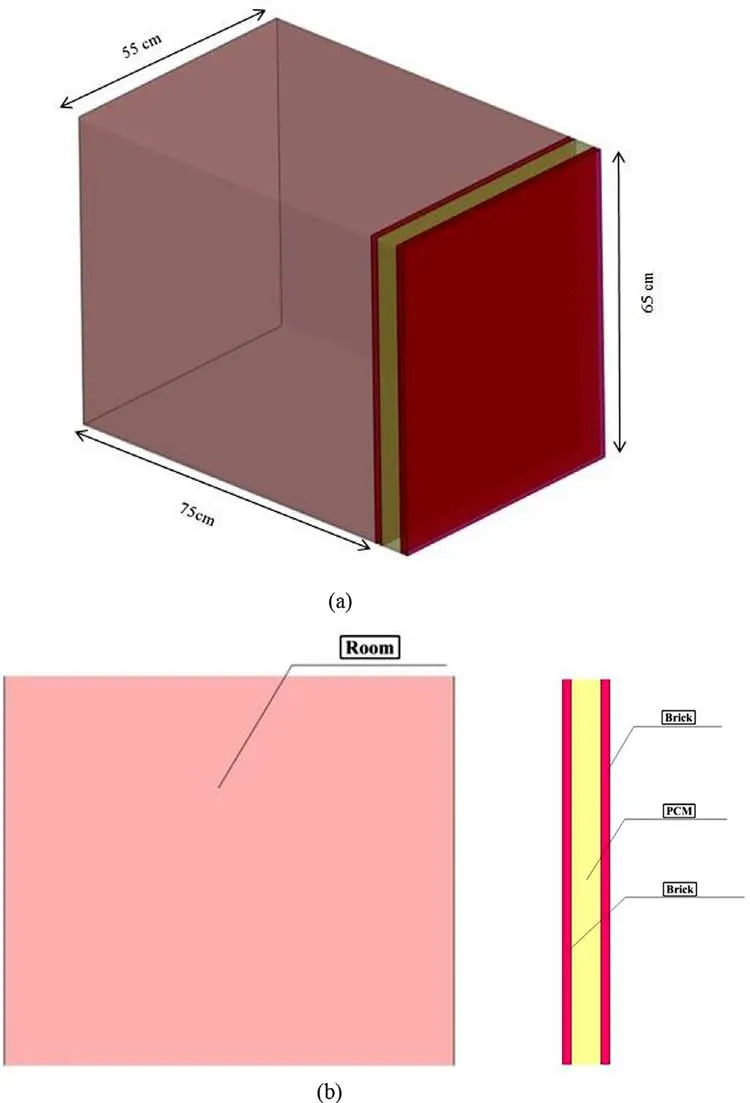
Fig. 1. Geometry of modeling.

The expressionsuandvare the velocity values in the direction of the coordinate axis. In the above equation,μ,ρ,Pandgrepresent density, fluid viscosity, pressure, and gravity acceleration, respectively. The defining variableScan be applied to make the velocity equal to zero in the momentum equation used in the enthalpy-porosity method. In other words, by defining the termSin the momentum equation in the sink statementsSvandSu,the zero velocity conditions can be met. The velocity should fall down to zero gradually. In this way, the finite velocity is reduced gradually in the liquid phase when there is a phase change and the liquid becomes solid. By using Darcy’s law as well as Kozeny-Carman equation, the fluid motion in a porosity medium has been studied:

A constant value of isb0 applied to prevent the denominator from becoming zero when the porosity is zero and its value is usually consideredb0 = 0.001. The coefficientCis considered to be in the range between 104 and 107.

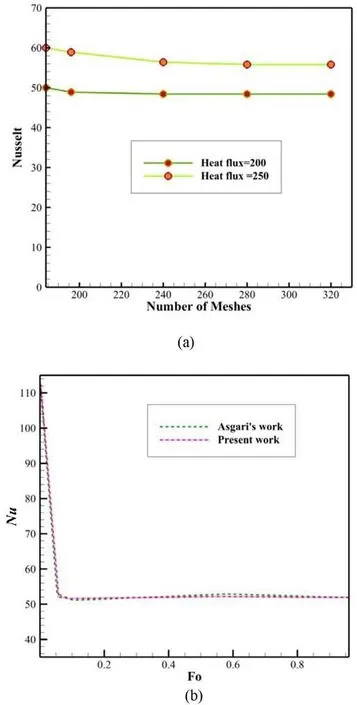
Fig. 2. The validation ( a ) of the number of meshes ( b ).

Tsis the temperature at which the PCM is completely solid andTlis the temperature at which the PCM is in the liquid phase. Since the solution to the problem is based on density changes, these changes are also evaluated in terms of temperature.

Fig. 3. Comparison for Cavity containing phase change materials and those without them.

Table 1 The physical properties of RT22, RT26, brick, and aluminum

whereβrepresents the coefficient of thermal expansion.

Since the convective effects in the melting process of PCMs are predictable, in order to better describe the heat transfer impact on the results, dimensionless numbers such as Nusselt, Reynolds,Rayleigh, and Stephen have been employed.

In order to investigate the effects of changes in heat capacity and thermal conductivity of PCMs, according to Table 1 , thermal performance of materials should be studied to determine the most optimal physical properties of PCMs to store thermal energy and thermal balance inside the cavity.

In order to validate computer calculations and mathematical analysis, results related to different number of meshes have been studied. In the two-dimensional simulation of PCMs with a layer thickness of 15 mm, the Nusselt number was examined for the number of meshes 234316 and 324878 which was found that the difference between the Nusselt numbers was only 2%. Therefore, in order to reduce the volume of computer calculations, simulations were performed with a smaller number of meshes (See Fig. 2 a).Moreover, a comparison has been made between the obtained results with those provided by Asgari et al. [19] , to which a good agreement was observed (See Fig. 2 b).

Fig. 4. Liquid fraction contour for paraffins with different thermal conductivity: ( a ) - k = 0.4, ( b ) - k = 0.3, ( c ) - k = 0.2.

There is a lack of thermal research on using bricks and PCMs RT21 and RT26 in relation to the effects of radiation and applied heat to the building, in this paper an attempt has been made to study turbid layers of brick that are exposed to the heat flux and solar radiation. Also, by using PCMs embedded between the brick layers, the scope of research and thermal analysis of building structures can be improved.

Figure 3 shows the comparison between the effects of different thicknesses of PCMs under constant heat flux. In general, as the thickness increases, the temperature distribution in the chamber becomes more uniform and temperature peak values also decrease. This happens in two stages, before the phase change and during the phase change. It actually acts as a thermal regulator before the PCM changes phase and as the thickness of PCMs increases, the rate of temperature penetration into the chamber decreases. This prevents the temperature inside the chamber from rising much during the intended time. On the other hand, if the phase changes, by absorbing energy it retains a significant amount of heat and prevents the ambient heat from penetrating into the chamber.

In the field of temperature regulation and energy storage process time and physical properties of materials are issues of high importance. Generally, PCMs have very low thermal conductivity.This slowness is useful in thermal conductivity when the purpose of using these materials is only thermal regulation, but in most cases, the main purpose of using these materials is to store thermal energy, and consequently thermal regulation in the desired environment is the main purpose of using these materials. For this purpose, the thermal evaluation was performed for the paraffinic material RT21 with three thermal conductivity of 0.3, 0.4, and 0.5 W / m.k . As the conductivity increases at the beginning of the heating process, the dominant conductive heat transfer time increases and this shows that rising the conductivity leads to an increase in the effects of viscosity force. But beyond these differences, the amount of temperature change is not very large over time. Eventually the effects of buoyancy force overcome the viscosity force, and the heat goes up and finally the heat transferred to the chamber is placed more in upper areas and consequently the temperature of middle and lower areas of the chamber becomes lower than the upper area. The heat penetrates to these areas over a long period of time (See Fig. 4 ).

In this study, the melting rate would change by applying different values of constant heat flux. Material movement is likely to occur at the fluid-solid interface and depending on the type of flow, new conditions must be analyzed. By using Rayleigh dimensionless number, the type of fluid flow can be evaluated. By increasing the heat flux to 250 W/cm2, the maximum Rayleigh values become 106, which indicates the current range is in the laminar flow range. But the contrast between fluid and solid at the fluid-solid interface causes the Nusselt values, which represent the rate of heat transfer, to drop at the beginning of the melting process. In fact, this is related to the thermal resistance at the beginning of the phase change and then for a short time it takes an ascending trend but finally, by decreasing the effects of conductive heat transfer, a descending trend is formed for Nusselt values. It is worth noting that, increasing the amount of heat flux leads to a rise in the heat transfer rate and consequently the amount of Nusselt number increases. Undoubtedly, by increasing and decreasing the temperature, the thermal behavior of PCMs also changes, so when the temperature rises, the effects of convective heat transfer increase and the material changes its phase over a reduced amount of time. One way of analyzing this situation is to look at Stefan number. With the help of this dimensionless number,it can be stated how much energy is stored in these materials under different heat fluxes and heat absorption by PCMs. In fact,based on capacity enthalpy of PCMs during the phase change, a suitable thermal evaluation can be performed, because the main subject of energy analysis and study in phase change processes is the expression and study of capacity enthalpy. Due to the fact that the phase change does not occur exactly at the same temperature, it is difficult to investigate and track the solid-liquid interface. Therefore, in order to calculate the energy, enthalpy can be used. By increasing the heat flux values of the hot wall from 150 W/cm2to 250 W/cm2, it is observed that more energy is received by PCMs during the phase change. This means that by increasing the temperature and creating a greater temperature difference between the solid phase temperature and the temperature inside the chamber, the materials tendency to absorb and store energy also enhances and as a result, the melting rate of materials increases(See Fig. 5 ).

The desired simulation has been done between three paraffins under constant temperature, and the same thickness and thermal conductivity. In this analogy, three paraffins with a heat capacity of 160 0, 20 0 0 and 240 0 J/(kg ·K) were thermally examined. After heating for 20 0 0 seconds, it was discovered that the highest amount of absorbed heat and molten material was for paraffin which has the highest heat capacity. The reason for this phenomenon is that the material is more inclined to absorb the heat which causes the PCMs with this thermal property to change phase in larger amounts after absorbing and retaining the heat, and finally storing a higher volume of energy. There is another way to explain this issue that the heat capacity has a significant effect on the kinetics of the melting process of PCMs. Therefore, in the end, the effect of buoyancy overcomes the viscosity force with more power and causes the material to melt in a curved and upward manner (See Fig. 6 ).

Along with the applications of PCMs in the field of thermal control and energy, these materials can also be used to control the thermal condition and temperature in the construction industry and even the medical industry. For this purpose, by comparing the two organic substances RT26 and RT21, their heat absorption was studied. In this simulation, by applying a constant heat flux to the materials which are located above and below of each other,it was observed that the heat moves towards a PCM which has a higher melting temperature. This means the heat transfer is from the brick wall of the chamber to the PCM which maintains its primary type of heat transfer conduction. The absorption of the heat by RT21 and the beginning of the phase change process, the type of heat transfer would be convective, which gradually leads to viscous effects get weakened over time and in the area of the thermal boundary layer, the buoyancy force is manifested. Therefore,the heat is mostly absorbed by a substance that is able to maintain its primary state for a longer period of time (See Fig. 7 ).

By applying heat flux and radiant heat simultaneously, the heat transfer rate increases. This happens when the temperature and the effects of buoyancy increases. In fact, when the chamber is exposed to radiation, by increasing the temperature, the effects of viscosity and chemical bonds of PCMs in solid phase are weakened. Therefore with each breaking of the chemical bonds, the effects of conductive heat transfer reduce and the convective heat transfer increases. However, if the chamber wall contains transparent PCMs, then the amount of radiation effects will be more visible and stronger heat transfer will occur. In fact, due to the transparency, the heat penetration increases and on the other hand,PCMs become semi-transparent after melting, which makes the radiation effects to be the main cause of heat transfer and finally change the state of the material (See Fig. 8 ).

Fig. 5. The effects of temperature changes on material phase change: ( a ) Solidification, ( b ) melting.

In this numerical work with the aim of investigating the effects of specific heat capacity and changes in the thermal conductivity of PCMs, the thermal energy storage of PCMs under the melting process has been studied. In the intended process, by examining the different thicknesses of PCMs, the effects of temperature adjustment of the chamber internal area with the help of these materials have been analyzed. The ANSYS-Fluent engineering software has been employed. In this simulation, due to the buoyancy effects and its interaction with viscosity force, an attempt has been made to use the Presto mode in order to calculate the pressure parameter correctly. Also, the simulation of radiant heat transfer has been investigated surface to surface mode by considering the transparency of the walls and the semi transparency of the liquid material. By employing turbid layers and embedding PCMs with high latent heat in front of the heat source, and also considering the radiation and solar radiation load, the lack of research and scientific analysis of heat penetration and heat dissipation quality inside the building will be addressed. Furthermore, by applying different heat fluxes, the heat penetration changes have been investigated.

Fig. 6. Temperature contour of cavity with brick walls containing paraffin with different heat capacities: ( a ) Cp = 1500 J/(kg ·K), ( b ) Cp = 2000 J/(kg ·K), ( c ) Cp = 2500 J/(kg ·K).

Fig. 7. Temperature contour and liquid fraction in the heating process of two chambers with brick walls and two layers of paraffin, chamber ( a ) RT26 at the top and RT21 at the bottom, ( b ) RT21 at the top and RT26 at the bottom

(1) Increasing the viscosity causes the main role of PCMs to be in the form of thermal regulators

(2) At constant heat flux, increasing the Stefan number enhances the convective heat transfer

(3) Applying the effects of radiation reduces the thermal resistance of PCMs

(4) With the use of turbid layers of bricks and phase change materials, the excessive heat penetration can be prevented, which reduces the temperature peak in the chamber by 24.1%.

(5) By embedding PCMS between the brick layers, the heat flux will penetrate to the chamber with a significant time delay compared to the model without phase change materials.

(6) Due to the isothermal process of solidification melting of PCMs for a relatively long time, the temperature inside the chamber remains constant.

Fig. 8. Liquid fraction contour of heating process with constant flux in the presence of solar radiation load inside the chamber containing phase change materials

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.