齿面点蚀对航空螺旋锥齿轮副啮合特性影响分析

王笑乐，卢剑伟，蔡云庆，王红州

1.安徽农业大学，安徽 合肥 230036

2.合肥工业大学，安徽 合肥 230009

螺旋锥齿轮作为一种重要的齿轮传动零件，被广泛地应用于航空航天和汽车等行业的传动系统中。与直齿圆柱齿轮相比，螺旋锥齿轮常用于相交轴间的动力传送，工作时为连续的节线接触，具有平稳的传递性，噪声和振动都非常小，适合高速传动，因此其啮合特性直接影响系统的传动稳定性[1]。随着现代航空工业对齿轮传动要求的日趋严格，螺旋锥齿轮副承载工况更加恶劣复杂，服役过程中易产生齿面点蚀故障，显著影响装备的动力性、经济性、平顺性和可靠性[2]。而且，航空器在加工制造方面具有更高的精密性，一旦发生点蚀情况，则对其传动系统的工作产生重要影响，甚至引起航空航天事故的发生[3]。因此，深入研究齿面点蚀对螺旋锥齿轮副啮合特性的影响在航空航天领域具有重要意义[4]。

螺旋锥齿轮相比圆柱齿轮具有更为复杂的几何特征和齿面形貌，点蚀的产生进一步加剧了接触分析的复杂程度，有限元法是目前研究其故障状态下啮合特性的主要技术手段[5-6]。马鹏程、汪中厚等基于Abaqus软件研究了齿面椭球形点蚀对弧齿锥齿轮副承载传动误差的影响规律[7]。李秋泽等以高速动车组弧齿锥齿轮疲劳点蚀为研究对象，统计了点蚀故障的发生位置，并基于加载啮合试验分析了齿面接触应力与接触面积的变化规律[8]。冯松等对比研究了齿面磨损、微点蚀和宏观点蚀对渐开线直齿圆柱齿轮副啮合刚度的影响[9]。王晓鹏建立了齿面微点蚀状态下的法向接触刚度预估模型，计算了渐开线齿轮副不同程度点蚀状态下的法向接触刚度[10]。赵鑫等利用势能法计算了渐开线直齿轮副齿面椭圆形点蚀故障下的啮合刚度[11]。罗棚等运用Abaqus软件建立了直齿圆柱齿轮副啮合模型，分别获得了健康齿、圆点蚀和方形点蚀故障齿的最大接触应力，并基于试验研究了不同点蚀程度对齿轮系统振动噪声的影响规律[12]。

现阶段，分析齿面点蚀对螺旋锥齿轮副啮合特性影响规律的研究仍较少见。为此，本文以刀倾半展成法加工的螺旋锥齿轮副为研究对象，基于承载接触分析技术（LTCA）研究了不同载荷下不同位置点蚀对齿轮副啮合印痕、动态传动误差、接触应力等啮合特性的影响规律，为后续研究航空航天飞行器传动系统的工作原理及可靠性分析奠定基础。

1 螺旋锥齿轮副承载分析模型

1.1 螺旋锥齿轮副参数及实体模型

本文所研究的某航空减速器螺旋锥齿轮副采用小轮下偏置，几何参数见表1。其中，大轮采用成形法、小轮采用刀倾法加工，是国内外航空航天专用螺旋锥齿轮副常见加工方式，大小轮的加工参数见表2、表3。

表1 螺旋锥齿轮副几何参数Table 1 Geometric parameters of the hypoid gear pair

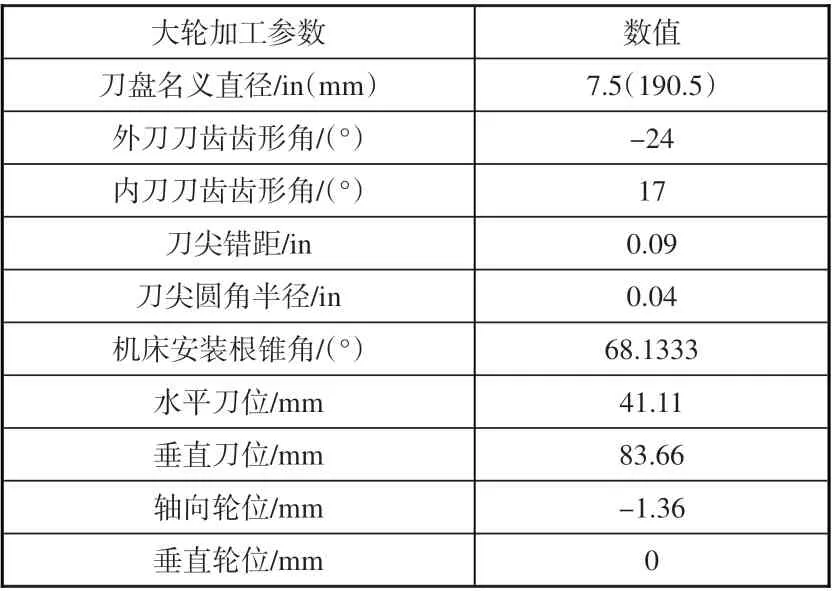
表2 大轮加工参数Table 2 Processing parameters of the gear

表3 小轮加工参数Table 3 Processing parameters of the pinion

研究螺旋锥齿轮加工过程的数学表达，基于Matlab 软件建立机床加工过程的仿真数学模型，计算加工参数，完成虚拟加工，根据加工程序计算完成螺旋锥齿轮副含齿根过渡曲面的全齿面精确建模，求解得到大、小轮齿面点云坐标[13]。加工仿真非本文研究重点，故不再赘述。将获得的离散点云采用曲面拟合的方式生成含齿根过渡曲面大、小轮齿面，分别建立其三维模型，如图1、图2所示。

图1 大轮三维模型Fig.1 3D model of the gear

图2 小轮三维模型Fig.2 3D model of the pinion

1.2 螺旋锥齿轮副有限元模型

将大小轮三维模型导入Hypermesh 软件进行网格划分，综合考虑计算精度及效率，建立小轮全齿、大轮6 齿网格模型，如图3、图4 所示。为了在齿轮表面准确构造出点蚀特征，对工作齿面进行网格细化加密，控制单元长度小于0.2mm、单元厚度小于0.1mm，小轮工作齿面网格细节如图5所示。

图3 大轮有限元网格模型Fig.3 Finite element mesh model of the gear

图4 小轮有限元网格模型Fig.4 Finite element mesh model of the pinion

图5 小轮工作齿面网格模型Fig.5 Finite element mesh model of the working surface of the pinion

将大、小轮网格模型导入有限元分析软件Abaqus，完成分析类型、材料属性、截面属性、分析步、场输出变量、历史输出变量、相互作用、边界条件及载荷等参数设置[14]，材料参数采用45钢参数，部分前处理参数设置见表4。

表4 部分前处理参数Table 4 Some preprocessing parameters

对螺旋锥齿轮副啮合过程进行仿真，要模拟大轮和小轮在静止不动时相互接触产生的啮合特性，由于齿侧间隙的存在，齿轮刚开始接触时可能存在啮合冲击现象。为使啮合冲击最小，迭代过程收敛，静态分析步选择staticgeneral 类型[15]，一般分为三个分析步，分别设置为：（1）约束小轮6个方向的自由度，将大轮绕轴线偏转微小角度，使大、小轮齿面接触。第(1)步设置时长为0.05s，初始增量步长设置为0.01，最大增量步长为0.05，最小增量步长为默认设置，最大增量步数设置为100。（2）释放小轮轴向自由度，固定大轮6个方向的自由度，将小轮绕轴线偏转微小角度，使大、小轮齿面接触，达到初始分析状态。第(2)步中步长相关设置同第(1)步。（3）同时释放大、小轮轴向自由度，小轮施加绕轴线固定角速度作为主动轮，大轮则作为从动轮，完成啮合。第(3)步根据小轮角速度及旋转角度，设定时间为0.85s，此时啮合至第6个齿，同时将初始增量步和最大增量步均设置为0.005，最大增量步数设置为1000。

2 螺旋锥齿轮副承载啮合分析

2.1 健康齿轮副啮合特性分析

分别为大轮施加100N•m、500N•m、1000N•m和3000N•m的4 种负载扭矩，为小轮添加大小为5rad/s 的驱动转速。经Abaqus软件仿真啮合过程，得到4种工况下健康齿面的啮合印痕，如图6所示，对比发现，随着载荷的增大，啮合区域的面积也不断增加，并向着两端和齿根扩展[16]。

图6 不同载荷下大轮齿面啮合印痕Fig.6 Meshing pattern on gear tooth surface under different loads

对比4种工况下齿轮副啮合至同一转角时的等效应力云图，如图7 所示，随着载荷增加，齿面应力集中区域向两端和齿根扩展，与啮合区域的变化特征一致，接触区域为扁平的椭圆形，应力最大区域位于椭圆中心。

图7 不同载荷下大轮齿面等效应力云图Fig.7 Meshing pattern on gear tooth surface under different loads

提取不同载荷工况下第四对啮合齿的齿面接触力，如图8所示。可以看出，螺旋锥齿轮齿面啮合力曲线近似于抛物线形状，且随着载荷的增加，齿面啮合力也相应增大。

图8 不同载荷下齿面啮合力Fig.8 Meshing force under different loads

在理想状态下，螺旋锥齿轮副的啮合传动是无误差的，但是实际中螺旋锥齿轮副瞬时传动比是不断变化的，因此存在传动误差。传动误差的定义为：当小轮转过一定角度时，大轮实际转角与理论转角之差。即

式中：δ为传动误差，Δφh1为小轮转角，Δφh2为大轮转角，z1为小轮齿数，z2为大轮齿数。

图9 为齿轮副在不同载荷下的齿轮传动误差，可以看出，不同载荷工况下的传动误差呈周期性波动，随着载荷的增加，传动误差幅值也逐渐增大。

图9 不同载荷下齿轮副传动误差Fig.9 Transmission error of the gear pair under different load

2.2 点蚀齿轮副啮合特性分析

本文研究的螺旋锥齿轮副小轮为主动轮，大轮为从动轮，齿数比为Z1/Z2 = 10/41，工作过程中小轮齿面啮合次数更多，更易发生磨损失效等情况，此外小轮凹面为工作面，相同载荷下凹面应力远大于凸面应力[17]，因此本文将点蚀模拟在小轮凹面。将大、小轮均划分为纯六面体网格，将齿面网格加密为4 层。根据500N•m 载荷工况下的齿面实际啮合区域，分别在A、B、C 三个位置进行模拟点蚀，如图10所示。

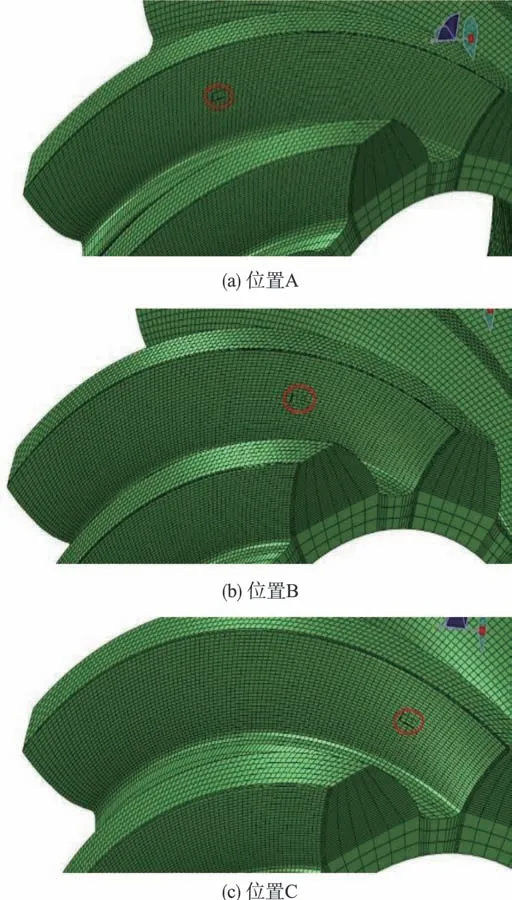
图10 齿面三种点蚀位置Fig.10 Three kinds position of pitting on tooth surface

以500N•m工况为例，对比点蚀齿轮副与健康齿轮副在点蚀位置时的等效应力云图，如图11 所示。对比发现，由于点蚀的存在，当齿轮啮合至该位置时，点蚀坑周围区域的等效应力显著增大，这将会导致点蚀面积进一步增大，从而加剧齿轮振动，对齿轮传动误差造成影响。

图11 健康和点蚀齿面接触应力对比Fig.11 Three kinds position of pitting on tooth surface

在500N•m载荷工况下，健康齿轮副与不同位置点蚀齿轮副第四对啮合齿啮合力变化如图12所示。可以看出，点蚀齿轮副与健康齿轮副齿面啮合力的变化趋势基本一致，呈抛物线形状。当齿轮啮合至点蚀位置时，相较于健康齿轮，不同位置点蚀齿轮副的齿面接触力均有不同程度的下降[18]。

图12 健康、点蚀齿轮副齿面啮合力Fig.12 Meshing force on tooth surface of healthy and pitting gear pair

图13为500N•m工况下不同位置点蚀齿轮副的传动误差曲线，可以看出，对于A、B、C三种点蚀位置，当齿面啮合至点蚀区域时，传动误差幅值均有所增大。将健康齿轮副传动误差与点蚀齿轮副传动误差进行求差，得到图14所示的误差曲线。

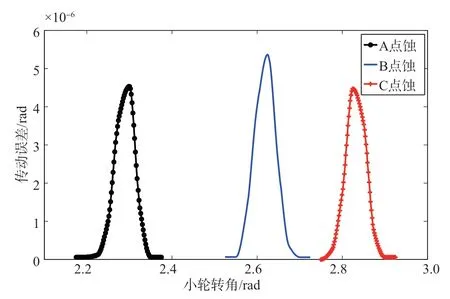
图13 不同位置点蚀齿轮副传动误差Fig.13 Transmission error of the gear pair at different pitting positions

从图14 中可以看出，相同载荷下，位于啮合区域中心位置的B 点蚀对传动误差的影响较大，位于啮合区域边缘位置的A、C点蚀影响较小，原因是当齿面啮合至B位置时，该区域为主要受力区，齿面应力相比较A、C区域更大，因此该位置点蚀对传动误差影响也较大，A、C 位置位于啮合边缘区域，此时有其他齿面分担载荷，点蚀位置的应力也相对较小，该位置的点蚀对传动误差影响较小，因此点蚀越靠近啮合边缘区域，对传动误差的影响越小。

图14 不同位置点蚀对传动误差的影响Fig.14 Influence of pitting at different positions on transmission error

为了深入分析不同载荷下点蚀对传动误差的影响，增加载荷数目，对齿轮副分别施加100N•m、300N•m、500N•m、1000N•m、3000N•m 和4000N•m 载荷，将不同载荷下的健康齿轮副传动误差与有点蚀传动误差求差，得到结果如图15所示。

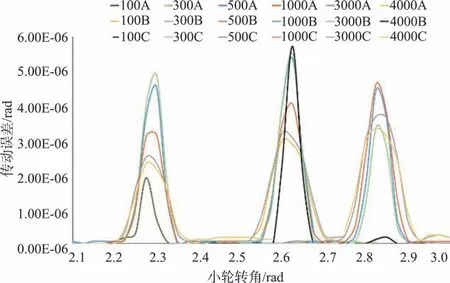
图15 不同位置点蚀齿轮副在不同载荷下传动误差Fig.15 Transmission error of pitting gear pairs in different positions under different loads

图15 中从左到右分别为A、B、C 三个点蚀位置的不同载荷对传动误差的影响曲线。可以看出，随着载荷增加，靠近齿面边缘的A、C点蚀处的传动误差呈先增大后减小的趋势，位于齿面中部的B 点蚀处的传动误差则一直增大。原因是啮合区随载荷增加向齿面边缘延伸，B 点蚀位于齿面中部，受接触区扩大的影响不大，传动误差增加主要受载荷增大引起。A、C 点蚀在低载荷时位于齿面边缘区域，但由于啮合区随载荷增加向两端延伸，A、C 点蚀逐渐向啮合区中心移动。对于A、C位置点蚀，在载荷增加前期载荷变化对传动误差的影响大于点蚀相对位置变化的影响，故在前期载荷增大时A、C影响曲线呈现增大的趋势，后期随着载荷的增大，A、C逐渐移向啮合区域中心位置，此时载荷变化对传动误差的影响小于相对位置移动造成的影响，故传动误差随着载荷的增大而逐渐减小。虽然载荷增大的后期点蚀对齿轮副传动误差的影响越来越小，但点蚀坑附近区域等效应力显著增大，甚至有可能超过齿轮许用应力，导致点蚀坑面积扩大，甚至发展到轮齿断裂的后果。

3 结论

本文以采用刀倾半展成法加工的螺旋锥齿轮副为对象，通过建立健康齿轮副和点蚀齿轮副的有限元模型，基于承载接触分析技术研究了不同位置齿面点蚀在不同工况下对螺旋锥齿轮副动态啮合特性的影响，获得以下结论：

（1）对于健康螺旋锥齿轮副，随载荷增加，齿面啮合区面积不断增大，接触区域及齿面应力集中区向两端和齿根扩展，传动误差幅值逐渐增大。

（2）螺旋锥齿轮副啮合至点蚀位置时，点蚀处附近区域应力显著增大，而点蚀位置齿面接触力相比较健康齿面有所下降，会造成点蚀位置区域面积不断增大，加剧齿轮振动。

（3）螺旋锥齿轮副啮合至点蚀位置时，传动误差绝对值有所增加，位于齿面中部位置的点蚀对传动误差影响较大，位于边缘区域的点蚀对传动误差影响较小。当点蚀位于齿面中部时，载荷越大，点蚀对传动误差的影响越小，但影响范围越广。

（4）将螺旋锥齿轮应用至航空航天领域时，应采取一定的手段避免点蚀情况的发生；一旦航空减速器中螺旋锥齿轮副发生点蚀，应及时采取补救措施或者更换相应零件，以便降低事故发生的概率，提升航天器性能的可靠性。