涡扇发动机缩尺风扇管道声学试验数据分析

夏烨，陆美慧，李旦望，纪良

1.中国航发商用航空发动机有限责任公司，上海 201108

2.上海商用飞机发动机工程技术研究中心，上海 201108

随着航空事业的不断发展，日益严重的航空噪声引起人们的普遍关注，航空噪声已成为噪声污染的重要来源，为了控制飞机噪声，国际民航组织和各国的适航机构相继颁布了飞机的噪声适航标准[1]。

飞机噪声除了机体振动噪声、起落架等噪声外[2-3]，一个最主要的噪声源就是发动机。随着涡扇发动机涵道比越来越高，发动机排气速度越来越低，风扇/压气机噪声逐渐成为发动机主要噪声[4]。风扇/压气机的气动噪声分为由叶片表面边界层及尾缘旋涡脱落、大气湍流干扰等因素引起的宽频噪声和由叶片与周期性来流相互作用等因素引起的离散噪声两种。对于高转速航空发动机的风扇/压气机，离散噪声占主导地位。对于亚声速的风扇/压气机，离散噪声一般是由来流作用于转子叶片本身的气动载荷或转子叶片尾迹与静子叶片及支杆等相互作用产生的，主要分布在叶片通过频率及其谐波处。对于超声速的风扇/压气机，除了上述噪声外，还有由叶片与超声速来流相互作用形成的激波噪声，主要分布在叶片转频频率及其倍频处。研究表明，激波噪声随着声源距离的增加不断衰减。

自20 世纪60 年代以来，人们对风扇/压气机噪声产生的机理进行了大量的研究。Tyler 和Sofrin[5]给出管道内旋转模态的概念及模态的传播和截止特性被普遍认为是这一研究的开始，为后来的发动机管道声传播理论研究奠定了重要基础。风扇管道中声模态信息可以反映管道声源，并且可以反映出声传播、衰减特征，因此已被广泛应用在声源判定和声传播测量方面。

Honeywell公司[6]通过对轴流管道风扇噪声模态的测量得到了风扇非最佳工况下非典型多重纯音、多重非纯音和由支撑结构产生的噪声的诊断。在声模态的测量中采用了周向均布的与管道壁面齐平安装的8支Kulite压力传感器阵列。

在北京航空航天大学高速压气机试验台进气消声实验室建成后，在上海飞机设计研究院短舱消声衬垫项目的支持下，王同庆、吴怀宇等对同样的声衬样件又一次进行了声学测量试验[7]。试验除了测量声衬的减噪量外，还分别利用在声衬前后周向均布的16 支传声器进行了压气机管道内声模态测量。

对风扇激波噪声的研究可追溯至20世纪70 年代。基于Whitham[8]弱激波理论，Hawkings[9]、Kurosake[10]等提出了跨声速转子激波噪声传播的一维预测模型。该模型针对二维叶栅，将激波系在二维平面的发展简化为一维规则锯齿波，得到激波在传播过程中的衰减规律。该模型揭示了激波噪声传播的主要机理，不足之处是模型几何与真实情况差异较大。无法考虑发动机进出口边界条件和叶片安装角误差对激波噪声的影响。这样忽略了各列激波之间的差异，导致激波噪声能量分布在风扇的通过频率及其谐波上，而真实的激波是不规则的，能量分散在风扇的轴频率及其谐波上。

针对进出口边界条件的问题，Hawkings[11]根据射线理论建立了考虑进口边界条件的模型，Tsai[12]将这一模型推广到非均匀介质的情况，两种模型都只考虑准三维边界条件的影响，假设噪声在由声射线包络的环形“管道”中传播，对激波强度的积分求解中引入非线性项，从而修正了线性射线理论。然而，由于模型中没有考虑叶片安装角以及激波强度径向分布的影响，故模型与真实的物理问题仍有一定差距。

Fisher 和Mc Alpine 等[13]考虑风扇叶片几何误差导致的不规则锯齿波的传播特性，可以描述激波噪声从叶片通过频率的倍频分散到轴频率倍频的现象，并能考虑激波与声衬的相互作用，但无法描述激波径向分布对噪声的影响。

在上述激波噪声解析预测模型中有较多的假设，存在不同程度的缺陷和一定的局限性。可用于预测激波噪声在风扇上游管道中的非线性传播过程，优点是能够利用较少的计算机资源快速获得比较准确的传播特性，非常适合工程上做快速评估，但对声源的详细激波结构的分析无能为力。

数值计算技术兴起之后，开始探索用计算流体力学（CFD）技术直接计算激波噪声的可能性。通过求解完整的物理方程，寻求激波噪声的传播特性，不受理论模型中假设条件的约束。由于风扇前缘激波系在转动坐标系中可以视为定常，因此激波噪声是罕见的可以用定常CFD 技术进行模拟的气动声学问题。若不关注各列激波之间的差异导致归并最终形成多重单音，可以在单个叶片通道中求解定常流体力学方程得到激波噪声传播特性。

在计算流体力学日趋成熟的背景下，利用数值方法分析激波噪声特性己具有很强的可操作性，国外发动机制造商也己开始在工程设计中采用这一方法。GE[14]、PW[15-16]等发动机公司的研究表明，用CFD预测激波噪声的产生和传播是可行的，甚至无黏的求解器也足以胜任。

1 管道声模态

转静干涉噪声是由上游的B片转子叶片尾迹与下游V片静子叶片相互作用，由静子上的载荷产生的，其可能的周向模态数如式（1）所示。

式中：s为通过频率阶数，q为作用在转子叶片上非定常脉动力的傅里叶阶数，可为任意整数，q=(0,±1,±2,…)。

获得可能存在的模态阶数之后，还需要判断这些模态是否传播，硬壁管道声传播的条件如式（2）所示。

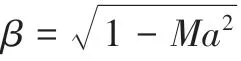
根据管道声传播条件可以得到管道的截止频率fcut-off，如式（3）所示。当频率大于截止频率，则该频率传播。

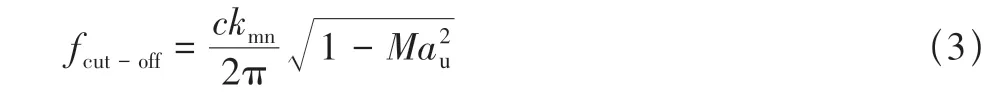
式中：Mau为轴流马赫数。

2 激波声功率

实际的风扇激波噪声表现为多重单音，分布于发动机轴频率的倍频。工程设计过程中，对问题进行适当简化，忽略制造安装误差，假设各叶片前缘的激波完全一致。因此，在计算中仅需要模拟单个叶片通道。在随转子转动的坐标系下，可以进一步简化为定常问题。

根据UTRC 的Prasad 等的方法，将短舱各轴向截面的激波噪声声功率作为量化评价参数。依据Morfey的定义，非均匀流动中的声强矢量如式（4）所示

式中：v为速度，ρ为密度，p为压力。γ为比热比，一般取1.4。

某截面S的声功率如式（5）所示。

考虑随风扇转子转动的旋转坐标系，进行坐标变换，得到式（6）

其中，Ω为转子角频率，B为转子叶片数。

假设声功率提取截面S垂直于x方向，获得式（7）

3 试验件介绍

风扇试验件由整流帽罩、单级风扇、内涵一级导流叶片、外涵一级导流叶片等组成，风扇叶片数18片，外涵静子叶片数48片，内涵进口导叶数98。

4 结果分析和讨论

本文对管道内测量频谱特性、管道声模态试验结果进行分析，并与数值结果进行对比。

4.1 管道声模态

4.1.1 测试方案

管道声模态测试有轴向Q1和Q2两圈测点，每圈周向均布40个测点。如图1所示。

图1 试验件测试示意图Fig.1 Sketch map of test

4.1.2 频谱特性

选取0.85、0.938、0.95和1.0的4个转速，两圈传声器0°位置处的频谱数据进行分析，如图2所示，红色表示靠近进气道位置，蓝色代表靠近风扇位置。1～4 分别表示转速从低到高。

从图2可以看出，对于1BPF和2BPF，在靠近声源位置，随着转速增大，声压级降低，在靠近进气道位置，随着转速增大，声压级先变大后减小，在0.938时最大。根据美国国家航空航天局（NASA）[17]的经验模型，当转子叶尖相对马赫数在1和1.4之间时，转静干涉单音噪声水平随着马赫数的增加而降低，如图3 所示。相对换算转速从0.85～1.0 叶尖相对马赫数分别为1.04、1.2、1.17和1.19，转静干涉单音噪声水平变化为降低—增加—降低。与NASA的经验模型预测结果一致。

图2 频谱结果Fig.2 Result of frequency spectrum

图3 单音噪声特性(NASA)Fig.3 Character of tone noise(NASA)

4.1.3 试验模态分解

对于风扇各频率的噪声来说，在单音未截止的情况下，BPF即叶片通过频率下的声压级最为显著。BPF的声压级可先通过式（8）计算出相应转速下的BPF，并在频谱中找出该频率对应的声压级（SPL）即可，以1BPF 为例，如图4 所示，红色标记出的为选中的BPF频率下的声压级。

图4 1BPF声压级示意图Fig.4 Sketch map of 1BPF sound pressure level

式中：RPM为转速，N为叶片数。

对于周向声模态，管道周向任意频率的复声压可以展开成多个周向模态的叠加，如式（9）所示。

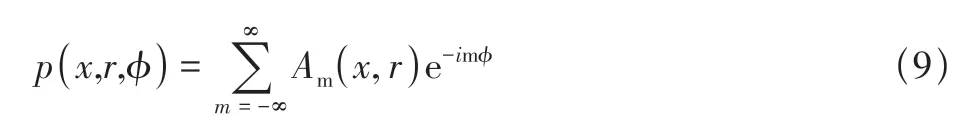
通常情况下，将Am=Am(x,r)记作周向模态的幅值，可通过周向的离散傅里叶变换（DFT）确定，如式（10）所示

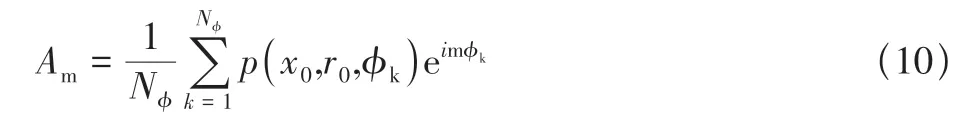
由于受试验测点数目限制，可以直接获得的周向模态阶数为-19～20，高阶模态出现叠混现象[18]，所以转静干涉噪声通过周向测量获得1BPF声模态信息。如图5所示，周向主要模态是18。从图5 中可知，当相对换算转速为0.938时，声压级最大。

图5 模态试验结果Fig.5 The test result of mode

4.1.4 数值模态分解

通过声速、密度、管道外径、轮毂比、转静子叶片数、转子旋转角速度、流动马赫数等参数信息，计算获得转静干涉1BPF模态信息，结果见表1。

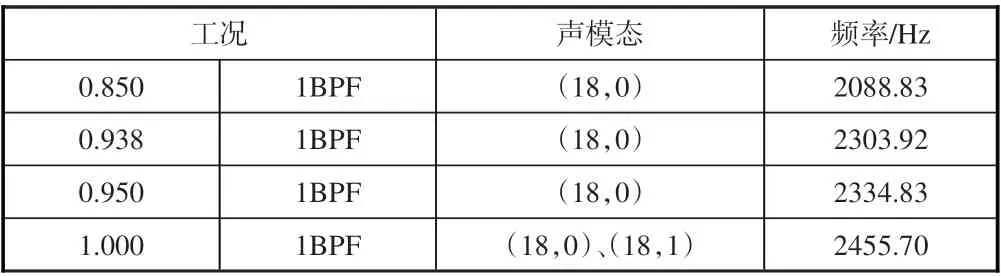
表1 模态数值结果Table 1 Simulation result of mode

4.2 激波噪声

4.2.1 测试方案如图6 所示，其中1～10 表示轴向布置了10 个传声器，在同一周向位置。4.2.2 频谱特性

图6 试验件测试示意图Fig.6 Sketch map of test

选取0.85、0.938、0.95和1.0的4个转速，对1和10位置的传声器频谱数据进行分析，如图7所示，红色代表1位置，蓝色代表10位置。符号1～4表示转速从低到高。从图7可以看出，在4个转速下都出现了激波噪声。

图7 频谱结果Fig.7 Result of frequency spectrum

4.2.3 试验结果

由于激波是转子叶片锁定的，它的频率是轴通过频率的整数倍，根据经验模型[19]，选取1BPF 以内的激波进行声能量计算。轴通过频率为RPM/60。选出的激波分量如图8 所示，红色标记出的为选中的激波各频率下的声压级。激波的总声压级即可通过将选出的激波分量合并得到，如式(11)所示。

图8 激波分量选取示意图Fig.8 Sketch map of shock noise component

式中：pi为激波分量的声压，pref为参考声压，n为选中的激波数量。

4.2.4 数值结果

各转速激波噪声压力云图如图9 所示。从图9 中可以看出，随着转速增大，激波强度增强，从正激波变为槽道激波。

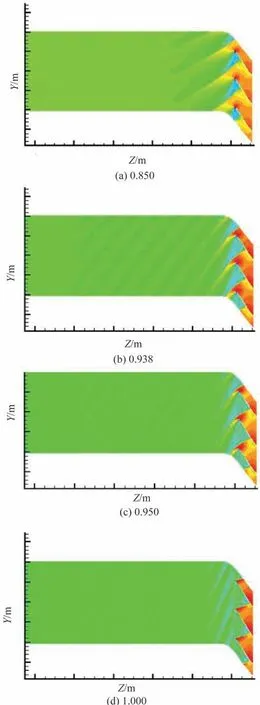
图9 压力云图Fig.9 Sketch map of pressure

激波声功率级轴向分布如图10所示，从图10中可以看出，激波声功率级沿轴向衰减，转速为0.85 时，靠近声源位置处强度仅次于0.938，随着轴向距离增加，激波快速衰减，与试验结果趋势一致。通过试验和数值对比，可以发现试验结果沿轴向呈波动状态，可能由进口反射导致。

图10 声功率对比Fig.10 Comparison between sound power level

5 结论

通过研究，可以得到以下结论：

（1）通过对比可以发现，对于一阶BPF，周向主要模态为18。试验结果与数值结果一致，后续可对高阶叠混效应进行相应分析，通过较少传声器获得相对高阶的周向模态信息。

（2）在分析的转速范围内，转静干涉噪声声压级随转速变化趋势与NASA 经验模型一致。随着转速增大，激波强度增强，从正激波变为槽道激波。

（3）激波声功率级沿轴向衰减，在转速为0.85时，随着轴向距离增加，激波快速衰减，与试验数据趋势一致。

（4）声功率级试验结果和数值结果幅值有差异，主要有两个原因：一是在进行声功率对比时，数值解对整个截面进行积分，试验结果是通过外壁面一点的结果近似获得整个截面的声功率级；二是进口有反射时，导致激波测量结果出现偏差。