高斯色噪声和谐波激励共同作用下耦合SD 振子的混沌研究1)

周碧柳 靳艳飞

(北京理工大学宇航学院,北京 100081)

引言

具有负刚度的非线性振子由于自身的多稳态属性一直受到机械设计领域的关注[1-3].作为一种典型的负刚度振子,耦合SD 振子[4]由两个SD 振子[5]刚性耦合而成,如图1 所示.该振子具有两个主要参数α和β,随着参数的变化,系统由光滑向不连续转迁,且呈现出多重屈曲和多重负刚度的动力学特性.基于上述特性,学者们对耦合SD 振子的动力学行为开展了广泛的研究[6-10].特别是由于具有多重负刚度的特性,该振子在工程设计中备受青睐[11-12].例如,基于耦合SD 振子设计的准零刚度被动隔振器[12],更接近理想的高静、低动刚度状态,更符合低频隔振概念.然而,负刚度的引入使隔振系统产生了同宿轨道,这可能引发系统产生复杂的混沌运动,对低频隔振造成很大的危害.由于混沌的参数区域很小,采用数值方法很难捕捉到混沌边界.为了克服数值方法的局限性,有必要使用解析的梅尔尼科夫理论来确定耦合SD 振子的混沌阈值.

经典的两稳态系统,例如达芬振子,由于具有明确的同宿轨道表达式,可以直接给出系统的混沌阈值[13-14].对于耦合SD 振子来说,由于其刚度项是超越函数[4],很难解析表示其同宿轨道.为了解决这一难题,Cao 等[15]提出了分段线性近似,并验证了其在分析确定性系统混沌阈值方面的有效性.由于随机因素广泛存在于现实环境中,并可能显著改变多稳态系统的动力学行为[16-17].因此,研究随机性对耦合SD 振子混沌的影响至关重要.关于白噪声和有界噪声激励对该类振子动力学行为的影响已有研究[18-19].然而,色噪声激励对耦合SD 振子混沌动力学的影响,迄今为止尚未见报道.有必要指出的是,在随机激励下,分段线性近似被推广来研究该类振子的混沌阈值是本文的出发点之一.

研究随机系统混沌动力学的方法较多,如最大李雅普诺夫指数、功率谱和梅尔尼科夫理论等.其中,梅尔尼科夫理论为混沌边界的预测提供了一种解析途径.众所周知,如果确定性系统的梅尔尼科夫函数存在简单零点[20],系统就会发生混沌.而随机系统的梅尔尼科夫函数是一个随机过程,很难直接讨论其简单零点的存在性.对于弱噪声激励下的光滑系统,通常采用均方准则[21]来解决这一问题.当噪声强度增大时,即使在均方意义下也很难探测到随机梅尔尼科夫过程的简单零点,在这种情况下,需要借助相流函数理论[22]来分析系统的混沌阈值.将均方准则和相流函数理论发展到随机非光滑系统,是本文的另一个出发点.

已有不少工作采用随机梅尔尼科夫理论,研究了噪声对多稳态系统混沌动力学的影响[23-27].例如,文献[27]讨论了三值噪声对达芬振子和约瑟夫森结系统混沌动力学的影响,并利用均方准则下的随机梅尔尼科夫理论给出了混沌的必要条件.然而,以往的研究大多是基于光滑系统的随机梅尔尼科夫分析.本文需要采用非光滑梅尔尼科夫方法,分析高斯色噪声和谐波激励共同作用下耦合SD 振子的混沌阈值.现有的非光滑梅尔尼科夫理论只适用于确定性非光滑系统[28-34]或有界噪声下[35]的随机非光滑系统.关于高斯色噪声和谐波激励共同作用下的随机非光滑梅尔尼科夫过程,尚未见报道.

本文主要发展了高斯色噪声和谐波激励共同作用下的随机非光滑梅尔尼科夫方法,并验证分段线性近似在研究随机激励下耦合SD 振子混沌运动时的有效性.首先,通过分段线性近似拟合了耦合SD 振子的刚度项并建立了分段近似系统.然后,发展了高斯色噪声和谐波激励共同作用下的随机非光滑梅尔尼科夫方法,并基于均方准则和相流函数理论给出了随机非光滑系统的混沌阈值条件.最后,讨论了弱噪声和强噪声情况下主要参数对耦合SD 振子的混沌运动的影响.

1 耦合SD 振子的动力学方程

Han 等[4]提出了耦合SD 振子,如图1 所示,质量为m的振子被一对刚度为k且原长为L的斜弹簧固定在刚性支撑上.刚性支撑的间距为 2a,质量块到刚性支撑的垂直距离为b.该质量块在谐波激励下沿X方向运动.本文在该模型的基础上考虑高斯色噪声激励的影响,可得系统的无量纲动力学方程

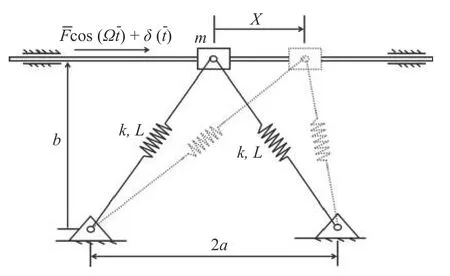
图1 耦合SD 振子的结构示意图Fig.1 The structural diagram of a coupled SD oscillator

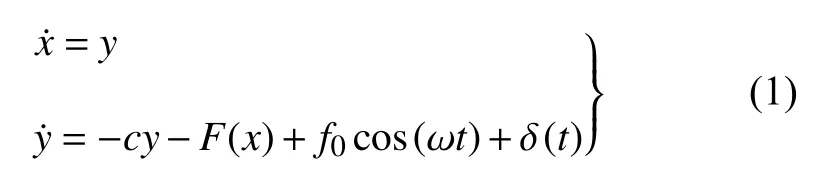
其中 δ(t)为高斯色噪声,其自相关函数定义如下[36]

其中 τ 表示噪声相关时间,D表示噪声强度,δ(t)的功率谱密度为

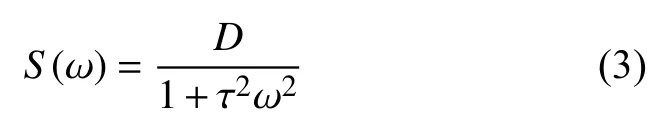
非线性刚度F(x)具有如下形式[4]

其中,α=a/L和 β=b/L为非负参数.

由式(4)可以看出F(x)是超越函数,随着α 和 β本文取α=0.3和 β=0.6来研究系统(1)在两稳态的变化系统(1)会呈现两稳态特性[37],不失一般性,下的混沌动力学.此时,方程F(x)=0有三个解,(0,0)和.为了解析研究系统(1)在同宿轨道附近的混沌动力学,引入如下形式的分段线性函数来拟合超越函数(4)

根据式(4)和式(5),图2 给出了函数F(x)和随x变化的曲线.

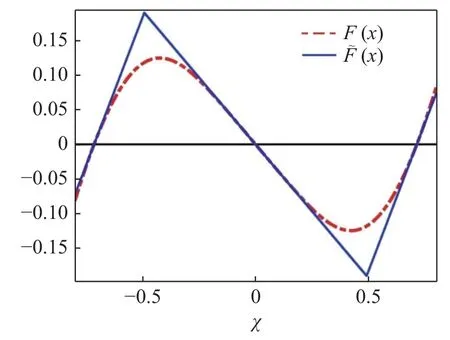
图2 函数 F(x)和的变化曲线.Fig.2 The plot of functions F(x)and

在不考虑激励和阻尼扰动的情况下,系统(1)对应的哈密顿系统具有如下势函数

其对应的图像如图3 所示.从图中很明显可以看出它具有两稳态的结构.

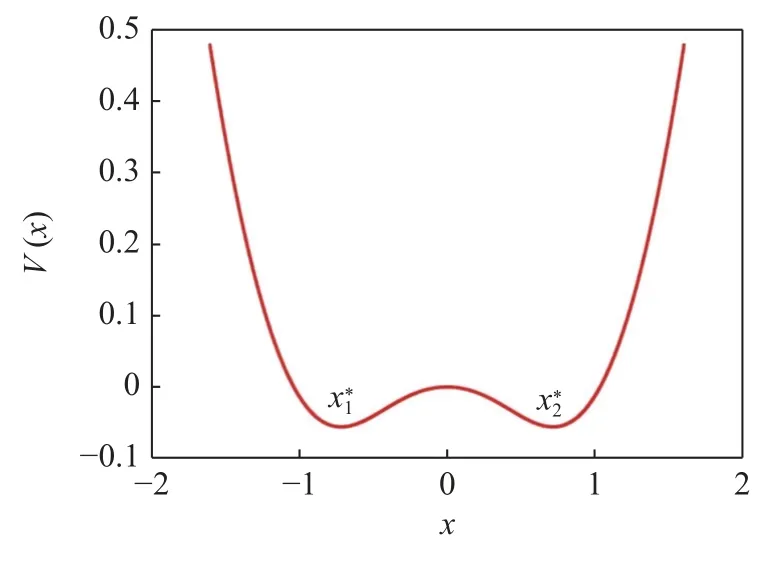
图3 势函数 V(x)Fig.3 The plot of the potential function V(x)

结合近似函数(5),相应分段近似系统可表示为

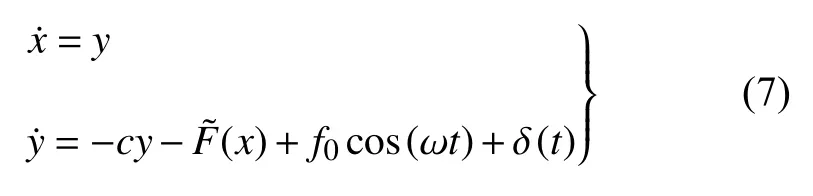
一般来说,从解析角度研究两稳态系统的混沌动力学,需要在同宿流形的基础上进行梅尔尼科夫积分.而分段线性近似是否有效,首先要验证原始系统(1)和分段系统(7)同宿轨道的近似度.

系统(1)的哈密顿函数如下

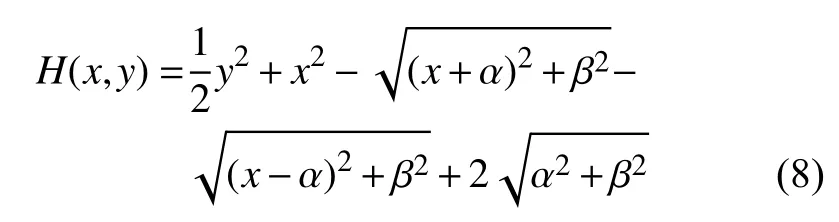
图4(a)表示哈密顿方程H(x,y)=E在不同能量值E下的相图.图中过鞍点(0,0)的红色曲线是同宿轨道,黑色曲线是同宿轨道外侧的一族周期轨道.蓝色曲线是同宿轨道内侧的两族周期轨道.

分段近似系统(7)的哈密顿函数可表示为

通过比较图4(a)和图4(b)可以发现,分段近似系统(7)和原系统(1)的哈密顿系统的相图吻合较好,因此下面利用系统(7)来分析原系统的混沌动力学.

图4 哈密顿方程的相图Fig.4 Phase portrait is plotted via Hamiltonian equation

2 高斯色噪声和谐波激励共同作用下非光滑系统的梅尔尼科夫方法

考虑如下高斯色噪声和谐波激励共同作用下的分段线性系统

其中

式中,wl(x,y)=0和wr(x,y)=0分别表示非光滑分界面Σl和Σr,g(x,y,t)表示确定性扰动,δ(t)是式(2)中定义的高斯色噪声.

系统(10)同宿轨道附近的稳定流形和不稳定流形如图5 所示.

图5 系统(10)同宿轨道附近的稳定流形与不稳定流形Fig.5 Stable and unstable manifolds near Homoclinic orbit of system(10)

在图5 中,过鞍点p2的红色曲线为同宿轨道,其解析表达式如下

其中 υ1(-Δ1)=υ2(-Δ1)∈Σr,υ2(Δ1)=υ3(Δ1)∈Σr.绿色稳定流形 υs(t;t0,ε)横截相交,υu(t;t0,ε)与υs(t;t0,ε)曲线为扰动后的轨道,此时稳定流形 υu(t;t0,ε)与不的距离表达式如下

其中M(t0)为系统(10)对应的随机梅尔尼科夫过程,可表示为

该随机过程由两部分构成,其中确定性部分为

随机部分为

这里

由于随机系统的梅尔尼科夫函数是一个随机过程,并不能直接讨论其零点的存在性.对于弱噪声激励下的随机光滑系统,通常使用均方准则来讨论梅尔尼科夫函数零点的存在性[21],下面将这种方法发展到随机非光滑系统.

在均方准则下,将Mξ(t0)考虑为高斯色噪声 δ(t)的输出,于是

其中h(t)是脉冲响应函数,其表达式如下

h(t)对应的频率响应函数为

根据式(19),可推出式(14)中随机部分Mξ的均方为

假设式(14)中确定性部分MG=,则系统(10)在弱噪声激励下的混沌阈值为

对于强噪声激励下的随机光滑系统,在均方准则下探测M(t0)的零点很困难,针对这种情况,往往需要结合相流函数理论[22]来分析系统的混沌.对于随机非光滑系统(10),其相流函数具有如下形式[22]

其中,ψ 为M(t0)关于时间的均值,根据文献[22]可求得

其中

相流函数Φ 代表系统(10)在所对应的相空间内,从稳定区域转移到不稳定区域的流量,稳定区域的流量流失的越多,系统(10)越容易发生混沌,Φ=0对应于系统(10)的混沌阈值.由于弱噪声很难造成相流函数的量变,因此通常使用ψ 的渐近函数来计算系统的混沌阈值.

当D→∞时,ψ 的渐近表达式为ψ=MG/2,则系统(10)在强噪声激励下的混沌阈值为

3 耦合SD 振子的混沌

为了分析不同色噪声强度对混沌的影响,本文围绕噪声强度D对色噪声作进一步划分,当D≪1时对应于弱噪声,反之对应于强噪声[38].

3.1 弱噪声情形

根据上一节的理论,可求得系统(7)的随机梅尔尼科夫过程如下

其中

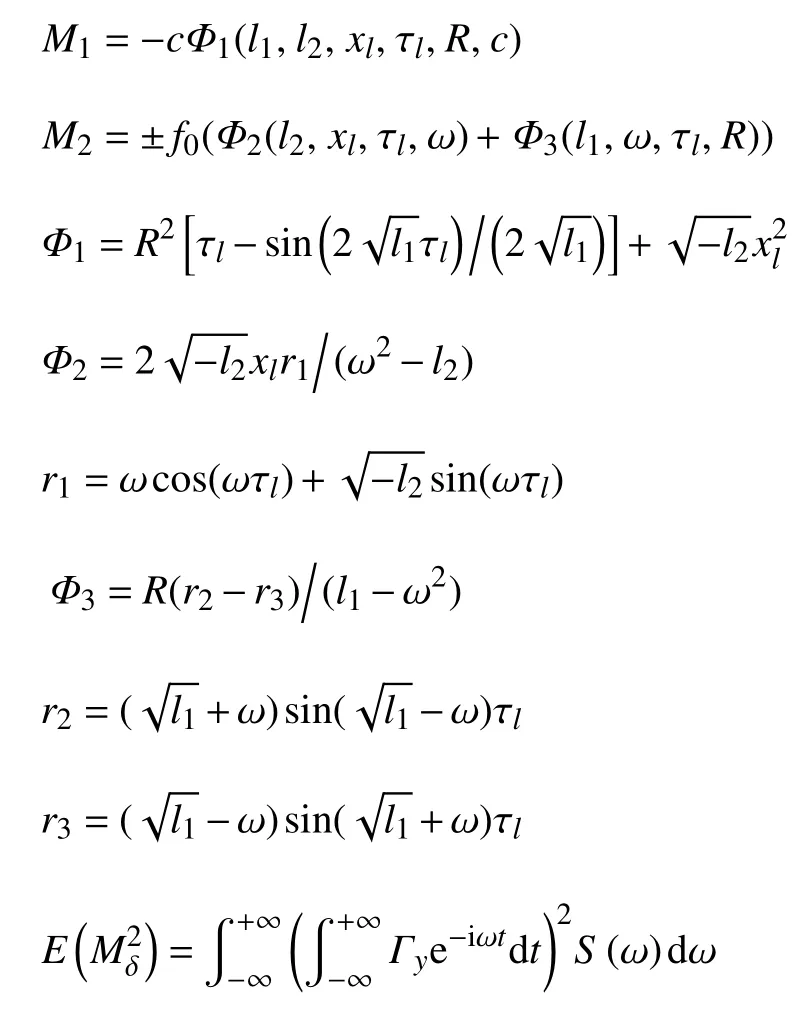
根据式(21),系统(7)在弱噪声情形下的混沌阈值为

根据条件(26),分段近似系统(7)的混沌阈值如图6 所示,该阈值用来预测原系统(1)的混沌.从图6可以看出,当(c,f0,D)落在曲面上侧区域时,原系统(1)将产生均方意义下的混沌.此外,图6 还表明随着谐波激励频率的增加,混沌区域逐渐减小.不失一般性,以图中ω=0.8为例来探讨原系统(1)的混沌.在ω=0.8,c=0.02和τ=0.5时,关于f0和D的混沌阈值如图7 所示,在该临界曲线上方的对应混沌区域,为了验证理论结果(26)的正确性.现从混沌区域选取一点(D,f0)=(0.0001,0.05),此时D≪1对应于弱噪声情形,在这种情况下,原系统(1)具有如图8 所示的smale 马蹄混沌吸引子.图9是相应的分段近似系统(7)的混沌吸引子.比较图8和图9,发现理论预测与数值结果吻合较好,证明了分段线性近似在弱噪声情形下是有效的.

图6 弱噪声情形下系统(7)的混沌阈值Fig.6 Chaos threshold for system (7) with weak noise

图7 弱噪声情形下在 ω=0.8 和 c=0.02 处系统(7)的混沌阈值Fig.7 Chaos threshold for system (7) with weak noise at ω=0.8 and c=0.02

图8 弱噪声情形原系统(1)的混沌Fig.8 Chaos for the original system (1) with weak noise

图8 弱噪声情形原系统(1)的混沌(续)Fig.8 Chaos for the original system (1) with weak noise (continued)

图9 弱噪声情形分段系统(7)的混沌Fig.9 Chaos for the piecewise linear system (7) with weak noise

固定D和ω ,分析高斯色噪声对混沌阈值的影响.图10 中的实线对应于谐波激励的混沌阈值,虚线、点划线和长虚线分别对应不同噪声强度下的混沌阈值.从图10 可知,随着噪声强度的增大混沌区域增大,这表明增大噪声强度更容易诱发混沌.当阻尼一定时,混沌阈值随噪声强度的增加而减小.

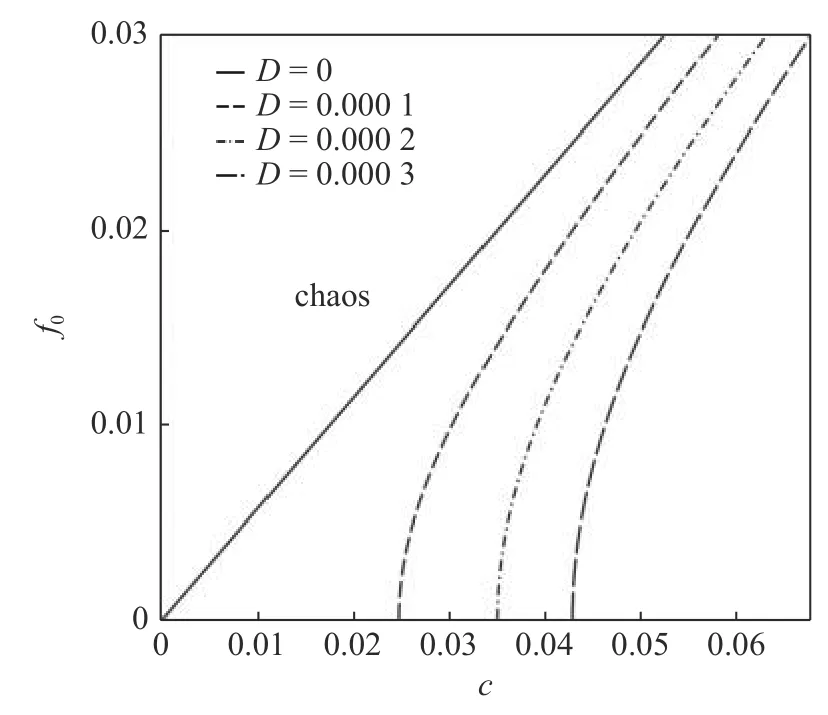
图10 固定 D和ω 时系统在弱噪声情形的混沌阈值Fig.10 Chaos threshold for system with weak noise when D and ω are fixed

3.2 强噪声情形

由条件(24),可求得系统(7)在强噪声激励下的混沌阈值为

根据条件(27),分段近似系统(7)的混沌阈值如图11 所示,该阈值用来预测原系统(1)的混沌.从图11 可以看出,当(c,f0,D)落在曲面下侧区域时,原系统(1)将产生混沌.此外,图11 还表明谐波激励频率对混沌区域的影响与弱噪声情况相同.不失一般性,以图中ω=5.2 为例来探讨原系统(1)的混沌.在 ω=5.2,c=0.05和τ=0.5时,关于f0和D的混沌阈值如图12 所示,在该临界曲线下方的对应混沌区域,为了验证理论结果(27)的正确性.从图12的混沌区域中选取一点(D,f0)=(3,60),此时D大于1 符合强噪声情形,值得注意的是,此时原系统(1)具有如图13 所示的非斯梅尔马蹄混沌.图14 是相应的分段近似系统(7)的混沌.比较图13 和图14,尽管强噪声对混沌吸引子的形状改变较大,但并没有改变混沌的本质属性,表明分段线性近似在强噪声情形下仍然有效.

图11 强噪声情形下系统(7)的混沌阈值Fig.11 Chaos threshold for system (7) with strong noise

图12 强噪声情形下在 ω=5.2 和 c=0.05 处系统(7)的混沌阈值Fig.12 Chaos threshold for system (7) with strong noise at ω=5.2 and c=0.05

图13 强噪声情形原系统(1)的混沌Fig.13 Chaos for the original system (1) with strong noise

图14 强噪声情形分段系统(7)的混沌Fig.14 Chaos for the piecewise linear system (7) with strong noise

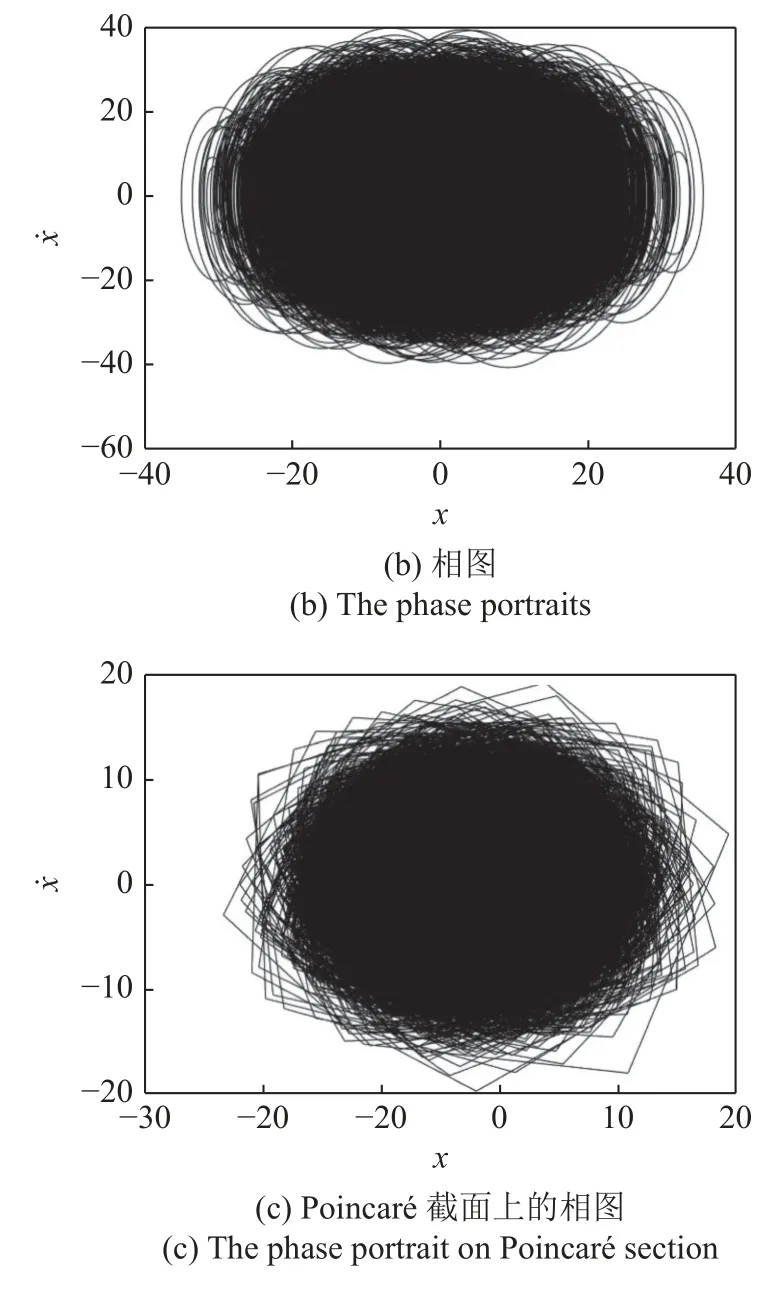
图14 强噪声情形分段系统(7)的混沌(续)Fig.14 Chaos for the piecewise linear system (7) with strong noise(continued)

固定D和ω ,分析高斯色噪声对混沌阈值的影响.图15 中的虚线、点划线和长虚线分别对应不同噪声强度下的混沌阈值.从图15 可知,强噪声情况下噪声强度对混沌区域的影响与弱噪声情况相同,但是当阻尼一定时,噪声强度对混沌阈值的影响与弱噪声情况相反.

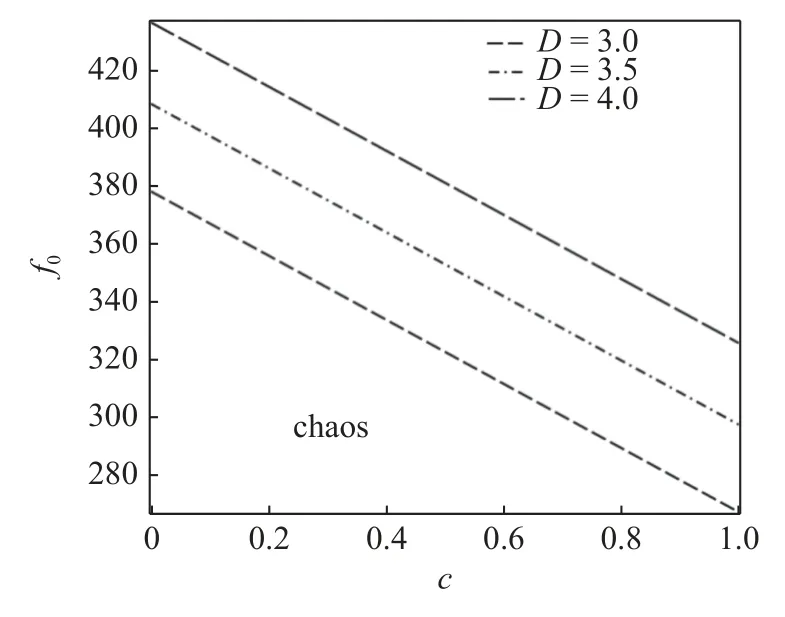
图15 固定 D和ω 时系统在强噪声情形的混沌阈值Fig.15 Chaos threshold for system with strong noise when D and ω are fixed

4 结论

混沌运动具有运动轨道不稳定及对初始条件敏感等特征,因此在工程实际问题中需要避免出现该“有害”现象,此时如果能确定混沌阈值的解析表达式,通过选取系统参数可使系统避免出现混沌.本文主要研究了高斯色噪声和谐波激励下耦合SD 振子的同宿混沌,发展了相应的非光滑系统的梅尔尼科夫分析方法,通过均方准则和相流函数理论获得了弱噪声和强噪声情况下的混沌阈值表达式,讨论了噪声强度和谐波激励对混沌阈值的影响.研究结果表明,分段近似系统与原光滑系统的混沌分析具有较好的一致性,进一步说明分段线性近似用于分析高斯色噪声下耦合SD 振子的混沌仍然有效.此外,高斯色噪声的引入可以扩展由谐波激励确定的混沌区域.本文的方法为研究随机激励下非光滑系统的混沌提供了一定的理论支持.

附录A