基于实测载荷谱的重载铁路货车车钩钩尾框剩余寿命预测1)

秦天宇 任鑫焱 胡飞飞 刘宇杰 奥 妮 阚前华 吴圣川 ,, 康国政

* (西南交通大学牵引动力国家重点实验室,成都 610031)

† (西南交通大学力学与航空航天学院,成都 610031)

引言

铁路跨区大载重运输是国民经济发展的重要命脉.随着中国经济的快速发展,铁路货运部门正大力推行重载高速机车来解决铁路货运能力日益不足的瓶颈.但由此带来的列车编组数量和轴重的迅速增加,使得货车各关键部件服役工况日趋严苛,运维频率增加[1].钩尾框作为传递列车纵向载荷的重要部件,其服役可靠性与铁路运输安全直接相关.在高频纵向动载荷的作用下极易萌生疲劳裂纹进而导致断裂失效,严重威胁重载列车的运行安全.众所周知,TB/T 456.3-2018 标准中规定,针对锻造钩尾框的较小表面缺陷可进行打磨清除,对于无法通过打磨清除的缺陷(如贯通裂纹)直接进行报废处理.但这往往会大幅度提高运维成本,同时检修不及时又易引发安全事故.因此,对钩尾框进行疲劳裂纹扩展寿命估算,进而准确评估钩尾框的服役状态,以此制定合理检修周期变得尤为重要[2-7].

当前,中国重载铁路主要以大秦线开行的2 万吨运煤专线为典型代表,其所采用C80 型重载货车的钩尾框型号为16/17 型.现役钩尾框的材料为锻造E 级钢,与传统的铸造钩尾框相比内部缺陷少,抗疲劳断裂性能更为优越.但长期暴露在雨水环境中产生的腐蚀坑将过早引起疲劳裂纹萌生和扩展[8].此外,锻造钩尾框的表面粗糙度较高,应力集中现象也比较严重,这也是导致表面萌生裂纹的重要因素之一,现场检修结果也表明后部弯角处萌生疲劳裂纹是钩尾框失效破坏的主要原因[3].长期以来,基于名义应力法的经典静强度设计思想为铁路结构提供了一种偏于保守的设计建议.然而,随着近些年来断裂力学的发展,世界上铁路发达国家和地区,例如欧洲、日本和中国等,均引入基于断裂力学的损伤容限来评估高速铁路伤损车轴等部件的剩余强度和疲劳寿命.例如,欧洲学者Beretta 等[8-9]在断裂力学框架下开展了高速铁路车轴完整性研究,并对EA4T车轴的服役周期决策、腐蚀环境影响等问题提出了若干理论模型;德国铁路公司采用断裂力学计算方法确定铁路车轴的检修周期,并进行了一定数量的全尺寸车轴测试验证计算结果[10];日本学者Makino等[11]将断裂力学引入新干线车轴完整性的研究中,对S38C 车轴的临界安全位置、剩余寿命乃至服役周期的决策进行了探讨;北京交通大学谢基龙等[12-13]基于线路实测谱,采用经典断裂力学的解析公式对重载货车铸造车钩部件(例如钩舌、钩尾框)进行了剩余寿命计算;西南交通大学吴圣川等[1,14-15]提出了一种将传统的名义应力法(无限寿命)与先进的损伤容限(有限寿命)相融合的阶梯疲劳评估方法(time-domain stepwise fatigue assessment,TSFA),并成功用于高速铁路车轴、转向架构架和磁悬浮列车悬浮架等铁路结构,受到国内外学者广泛关注[16-18].

然而,迄今为止在断裂力学框架下,特别是在基于实测载荷谱条件下,利用综合考虑了疲劳裂纹扩展三个阶段(近门槛值区、稳定扩展区与快速扩展区)的含裂纹张开闭合效应的剩余寿命评估模型对伤损钩尾框进行剩余寿命评估的研究还较少见.为此,本文以17 型重载钩尾框为研究对象,对钩尾框所使用的锻造E 级钢进行力学性能和断裂性能试验,建立含不同形貌比的初始裂纹钩尾框有限元模型,使用考虑裂纹扩展近门槛值区、稳定扩展区与快速扩展区的含张开裂纹闭合效应的NASGRO 方程,基于实测载荷谱转换后的分级载荷谱完成伤损钩尾框剩余寿命计算.

1 材料与性能试验

1.1 轴向拉伸性能

轴向拉伸试验可为裂纹扩展试验提供基本的力学性能参数,也为断裂力学仿真提供重要输入参数.拉伸试样根据GB/T 228.1—2010 标准进行设计,并根据锻造钩尾框受力状态进行取样,取样位置及尺寸如图1 所示.为确保数据可靠性和代表性,取3 个试样在MTS-809 材料试验机上执行,采用634.31 F-25引伸计并控制拉伸位移速率0.01 mm/s.对3 个拉伸数据进行平均处理,最终获得如图2 所示的锻造E 级钢的轴向拉伸应力-应变曲线,相关力学性能参数见表1[3].

图1 铸造E 级钢试样的取样位置及尺寸(单位:mm)Fig.1 Position and size of forged E-grade steel specimens (unit:mm)

从图2 和表1 中可以看出,货车车钩钩尾框用锻造E 级钢具有较高的屈服强度(ReL=848 MPa)和抗拉强度(Rm=940 MPa).根据TB/T 456.3—2018 标准,对钩尾框进行静强度校核,在施加最小极限载荷4005 kN 时,要求钩尾框的弹性变形量不能超过6.4 mm.基于试验获得锻造E 级钢的力学性能参数,通过有限元仿真计算得到钩尾框的最大弹性变形量为1.9 mm,仅为许用变形量的30%.由此可见,采用锻造E 级钢制造的货车车钩钩尾框在服役过程中具有较大的安全裕度.

图2 锻造E 级钢的单轴拉伸应力-应变曲线Fig.2 Uniaxial tensile stress-strain curve of forged E-grade steel

表1 钩尾框所用E 级钢的力学性能Table 1 Mechanical properties of E-grade steel used for hook tail frames

1.2 断裂性能试验

尽管如此,在实际异场服役工况和不当维修中,钩尾框仍会发生各种损伤或者缺陷.为了对含裂纹缺陷钩尾框进行准确剩余寿命评估,需要通过试验获得锻造E 级钢的裂纹扩展速率da/dN,裂纹扩展门槛值ΔKth和断裂韧度值KIC.裂纹扩展试样参考GB/T 6398—2017 进行设计,使用线切割在缺口处预制10 mm 初始裂纹,如图1.使用MTS-809 试验机开展试验,控制应力比R=0.1,频率为18 Hz.通过降K法进行门槛值试验,使用Paris 方程对扩展速率在10-6～10-7mm/cycle 的数据点进行线性拟合,10-7mm/cycle 截距所对应的应力强度因子范围ΔK即为ΔKth[3].

裂纹扩展模型直接决定了剩余寿命预测的准确性、可靠性与合理性.在铁路结构断裂力学计算中,常使用经典Paris 方程(式1)对裂纹扩展数据进行线性拟合,但该方程仅仅考虑了裂纹稳定扩展区,并未考虑裂纹近门槛区与快速扩展区.因此,本文采用综合考虑了裂纹扩展近门槛值区、稳定扩展区与快速扩展区的含裂纹闭合效应的NASGRO 方程,对钩尾框进行剩余寿命评估[14,19]

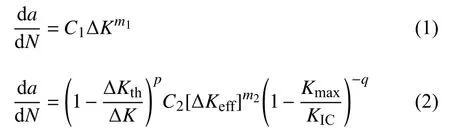
式中,Kmax为最大应力强度因子,C,m,p和q为材料常数,ΔKeff为有效应力强度因子范围,须注意公式中C1,C2,m1,m2表示不同的拟合数值.

钩尾框虽不承受压缩载荷,但由于裂纹张开应力σop的存在,相应会存在卸载应力区域.钩尾框表面裂纹在启裂和扩展的过程中,会在裂纹面附近产生循环塑性包迹,在卸载时包迹内外的塑性变形不能协调地回复,在拉应力的作用下也会有裂纹面提前闭合现象发生,即裂纹闭合效应[20-21].在实际工程问题中,认为考虑了裂纹闭合效应的有效应力强度因子范围ΔKeff是影响裂纹扩展更本质的参量

式中,R为应力比,f表示裂纹张开函数,Kop为裂纹张开应力强度因子,由钩尾框受力特点引入平面应变下的约束因子α=3.0,A0,A1,A2和A3是Newman 闭合函数系数,由下列公式计算[21]

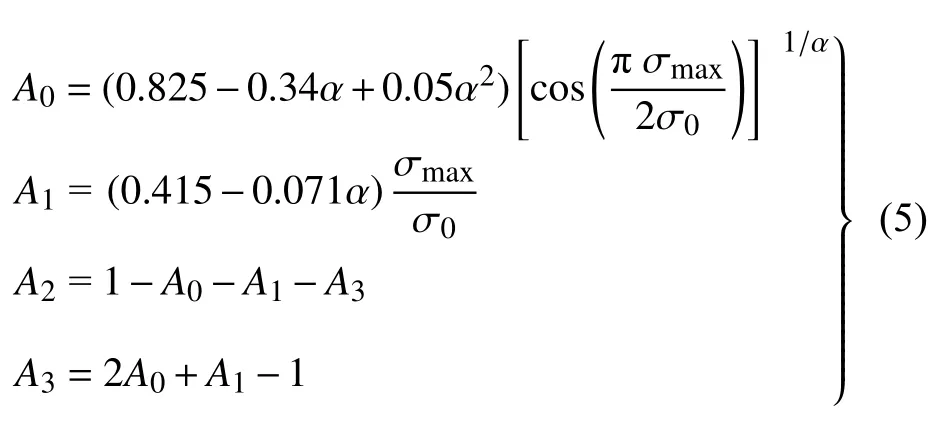
锻造E 级钢断裂韧性试验依据GB/T 21143—2014 进行设计,采用大量程范围的632.02 F-30 引伸计,应力比R=0.1,加载频率为16 Hz.在实际工程应用中,断裂韧性一般采用J积分间接来进行确定[22-23].完成试验后,使用NASGRO 公式对裂纹扩展速率试验数据进行拟合.

综合考虑了疲劳裂纹近门槛值区、稳定扩展区和快速扩展区的基于NASGRO 方程的裂纹扩展曲线如图3 所示[3].同时,与仅考虑了稳定扩展寿命的经典Paris 方程相比,NASGRO 方程估算寿命更加准确,表2 给出了NASGRO 方程的拟合结果.利用降K法测试出的裂纹扩展门槛值(ΔKth)和J积分法计算出的断裂韧性值(KIC)如表3 所示.

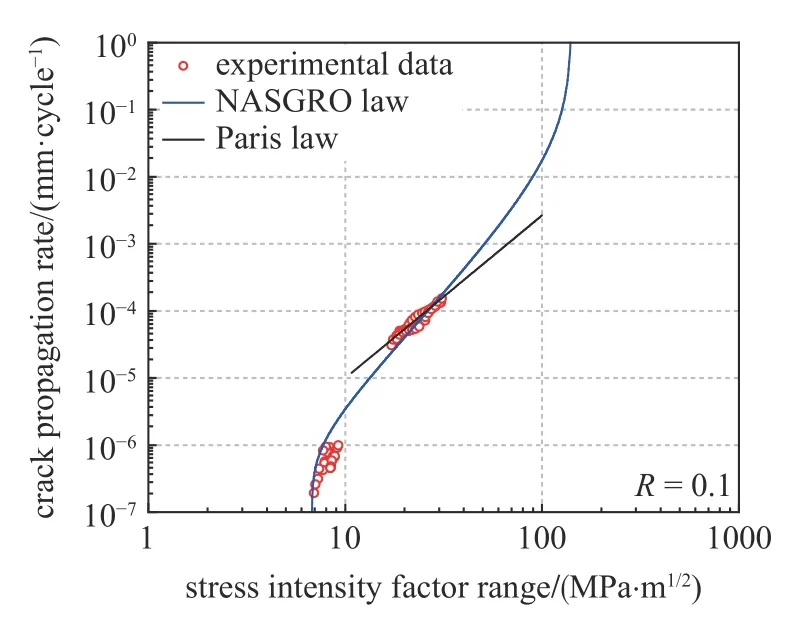
图3 应力比R =0.1 时的锻造E 级钢疲劳裂纹扩展速率实验和拟合曲线Fig.3 Experimental and fitting fatigue crack propagation rate curves of forged E-grade steel at R =0.1 stress ratio

表2 基于NASGRO 方程的疲劳断裂参数Table 2 Fatigue fracture parameters based on the NASGRO equation

表3 锻造E 级钢的裂纹扩展门槛值ΔKth 和断裂韧性值KICTable 3 Fatigue crack growth threshold ΔKth and fracture toughness KIC of forged E-grade steel

2 钩尾框计算模型

2.1 载荷及边界条件

对车钩缓冲装置几何模型进行网格划分,由于钩尾框等部件表面形状较为复杂,对非承载部位的小特征圆弧倒角进行几何光滑处理.综合考虑计算精度和收敛性,钩尾框关键部位使用六面体C3D8单元进行网格剖分,最大单元尺寸为4 mm,最小单元尺寸为0.8 mm,非关键分析部位以及其他零件使用四面体C3D4 单元进行过渡,整体模型共包含网格单元2 756 056 个,节点861 790 个.

将剖分好的有限单元网格模型导入ABAQUS软件,根据前述力学性能试验结果为计算模型赋予材料属性.如图4 中的钩缓装置,车辆实际服役过程中牵引力为对称传递:1 位侧车体牵引梁→从板→缓冲器→钩尾框承载面→钩尾销→钩体→钩舌→钩体→钩尾销→钩尾框承载面→缓冲器→从板→2 位侧车体牵引梁[24-27].为保证仿真过程最大限度与实际运行保持一致,根据车钩缓冲装置在使用过程中各部分的相互作用原理,约束一侧从板纵向x,横向y,垂向z三个方向的自由度,另一侧从板保留x向自由度进行载荷施加.为便于计算收敛需约束整个装配体零部件的y与z向自由度,并对钩尾框尾部承载面与从板之间建立弹性Beam 杆连接器来模拟缓冲器,具体如图4.最后分别设置钩舌、钩体、钩尾框之间接触属性为法向“硬”接触,来确保各零部件力的连续传递.

图4 断裂力学框架下钩尾框剩余寿命评估过程Fig.4 Remaining life assessment process for the hook tail frame in the fracture mechanics framework

载荷谱的选择直接影响最终的计算结果,薛海[28]将大秦线实测2 万吨重载货车车钩载荷-时间历程通过雨流计数法转化为若干段循环载荷,然后利用Goodman 公式修正为考虑应力比影响的脉动拉伸循环,最后通过式(6)和式(7)所示的S-N曲线和Miner 累积损伤等效原则,获得最终的等效5 级载荷谱.该载荷谱共包含载荷频次1614 次,测试里程15 000 km,如图5 所示.

图5 实测大秦线2 万吨重载5 级载荷谱[28]Fig.5 The actual measurement of 20 000 tons of heavy load grade 5 load spectrum of the Daqin railway[28]

式中,D为损伤数值,n1和n2分别为在不同载荷水平下的循环次数,N1和N2为对应载荷水平下循环至破坏的循环寿命,m和C表示与材料自身有关的常数.

2.2 初始裂纹预置

调研发现,裂纹多萌生于如图4 所示的钩尾框后部内侧弯角处.同时,有限元静力加载计算显示承受纵向拉伸时该内弯角部位应力最大.因此,为保证结果的可靠性,将初始裂纹引入该部位.根据受载特点认为该钩尾框裂纹主要为I 型张开裂纹,而工程中往往将裂纹等效为半椭圆型进行研究,通过a/c来描述裂纹的形貌特征,其中a和c分别表示裂纹的深度和半轴长度[29].本文将危险部位作为一个单独模块通过“tie”与主模型相连,使用C3D8 单元进行模块的网格剖分.为了研究不同形貌比裂纹对钩尾框剩余寿命的影响规律,分别植入a/c=0.3,0.5,0.8 三种形貌比的初始裂纹,并统一设置初始裂纹深度为2 mm,后续裂纹扩展深度分别为3,4,5,6,8,10,12,16,20 mm.最后,选取中间代表性0.5 形貌比的初始裂纹,减小其初始裂纹尺寸至0.5 mm,探究初始裂纹对剩余寿命计算结果的影响.

2.3 网格敏感性测试

裂纹前缘的网格尺寸在一定程度上会影响计算精度,为此将裂纹前缘细化为不同的尺寸进行网格敏感性分析.定义裂纹前缘网格单元沿裂纹扩展方向的边长b与裂纹深度a的比值b/a为影响裂纹尖端应力计算精度的变量,设置b/a=0.04,0.05,0.07,0.1,0.2.由于裂纹前缘具有应力奇异性,采用基于节点应力的外推法计算ΔK.利用ABAQUS 分析裂纹尖端的应力场可以得到裂纹前缘节点的应力值和距离,计算得到如图6 所示的应力强度因子K,采用最小二乘法拟合数据点可得到数据对之间的线性关系,最后将拟合直线延伸至纵坐标得到的截距即为ΔK的估计值[1].

图6 裂纹前缘应力分布和应力强度因子示意图Fig.6 Schematic diagram of stress distribution and stress intensity factor ahead of the crack tip

计算结果如图7 所示,当裂纹前缘加密层的网格尺寸小于裂纹深度的10%时,ΔK计算结果趋于一致,因此综合考虑计算精度和计算效率后,采用b/a=0.05 进行裂纹尖端网格划分.

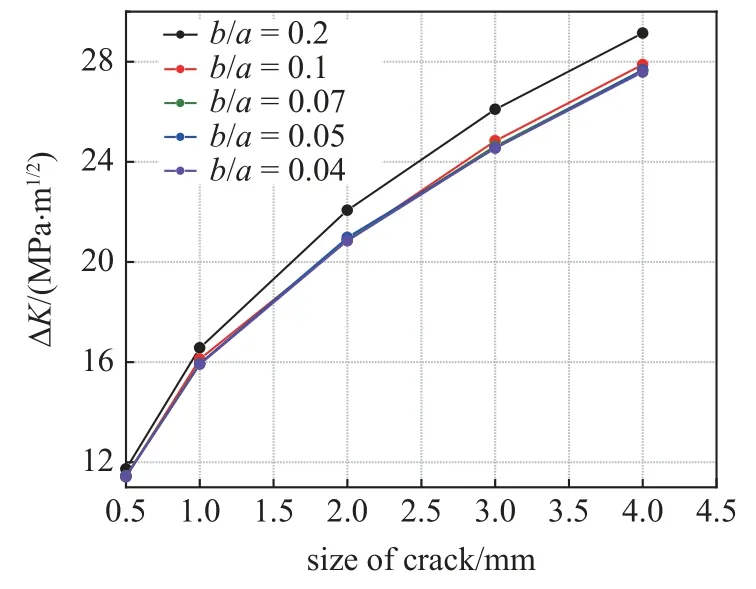
图7 不同深度裂纹网格敏感性计算Fig.7 Crack mesh sensitivity calculation at different depths

3 结果与分析

3.1 基于实测载荷谱的剩余寿命预测

众所周知,随着裂纹深度和载荷水平的变化,很难得到连续的裂纹扩展速率.因而在计算中通常假设裂纹在很小的扩展增量Δa范围内da/dN保持不变.基于以上假设进行裂纹扩展寿命计算时,为尽可能得到精确的数值解,各阶段的裂纹增量设置必须足够小.但受限于工作量和计算能力,只能采用更加保守的方法进行裂纹扩展寿命计算,即采用裂纹扩展各阶段中裂纹深度上限所对应的da/dN值进行计算.例如,计算2～3 mm 裂纹扩展剩余寿命时,使用的是3 mm 对应的da/dN.为了定量化讨论裂纹扩展规律,图8 和图9 分别给出了形貌比a/c=0.5 时ΔK和da/dN随裂纹深度的变化关系.

图8 裂纹尖端应力强度因子范围随裂纹深度变化趋势Fig.8 Trend of crack tip stress intensity factor with crack depth

图9 基于NASGRO 方程的裂纹扩展速率Fig.9 Crack propagation rate based on NASGRO equation

由图可知,计算的应力强度因子范围ΔK与裂纹扩展速率da/dN随着裂纹扩展尺寸的增大而不断增大.当裂纹扩展至8 mm 时扩展速率da/dN迅速上升,同时当裂纹深度扩展至20 mm 时在最大载荷1500 kN 的作用下,即使此时裂纹面积已经超过钩尾框截面积的1/2,ΔK仍未到达锻造E 级钢的断裂韧性值.由此可见,现役锻造钩尾框具有较大的抗断裂安全裕度.

由图10 中的不同形貌比下伤损钩尾框的剩余寿命曲线发现:同样裂纹深度下,裂纹形貌比越小,扩展寿命也越低;裂纹从2 mm 扩展至20 mm 时三种形貌比的剩余寿命分别为26,32,36 万公里,均不足一个段修期(一个段修期2 年,一年运行里程约20 万公里).与形貌比0.5 的裂纹相比,0.3 形貌比的剩余寿命减少了6 万公里,降低率约18.8%,而0.8 形貌比的剩余寿命相对增加了3.8 万公里,增长率约11.9%.由此可见,在相同的使用条件下形貌比越小的裂纹扩展速率越快,钩尾框的剩余寿命越短,在实际运维中必须重视长浅裂纹的危害.但不论何种形貌比当裂纹扩展至12 mm 后剩余寿命均急剧减少,分别仅占总扩展寿命的2.2%,4.0%,4.7%,因此可将12 mm 作为损伤容限止裂尺寸.

图10 初始裂纹深度为2 mm 时钩尾框的剩余寿命曲线Fig.10 Remaining life curves of the hook tail frame with the initial crack depth of 2 mm

3.2 检修周期建议

从上述讨论中可以看出,当以2 mm 作为初始裂纹深度时,即使在最小载荷下应力强度因子范围也远大于裂纹扩展门槛值.因此为研究近门槛区对裂纹扩展寿命的影响,在相同位置、相同载荷条件下对中间形貌比为0.5、深度0.5 mm (磁粉探伤所能检测到最小裂纹尺寸)的初始裂纹开展剩余寿命计算,计算结果如图11 所示.在最小载荷680 kN 的作用下0.5 mm 裂纹的ΔK为7.1 MPa·m1/2,此时裂纹处于近门槛区附近,该阶段的da/dN较小,总可服役里程为156 万公里.该计算结果跨越三个段修期,即使0.5 mm 小裂纹在段修时发生漏检事故仍可在后面检修中进行处理,从而可满足列车安全服役条件[30].

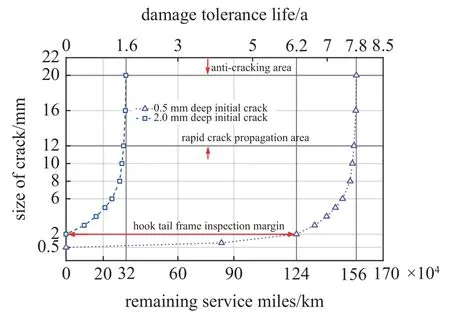
图11 不同深度初始裂纹钩尾框剩余寿命对比Fig.11 Comparison of remaining life of the hook tail frame with initial cracks at different depths

与之相反的是,三种形貌比下2 mm 初始裂纹的剩余寿命均不足一个段修期.因此,可认为当钩尾框出现2 mm 深度裂纹时,不论是何种形貌比都已经处于危险状态.已有研究表明[31],较高的表面粗糙度可视为一种表面缺陷,缺陷大小直接影响裂纹的萌生速度和初始裂纹尺寸.因此可采取打磨的方法对钩尾框危险部位进行处理来降低表面粗糙度,将在一定程度上提高其服役年限.

4 结论

本文以现役重载铁路货车车钩的钩尾框为对象,对锻造E 级钢开展材料力学和疲劳断裂性能试验,基于损伤容限思想估算了钩尾框剩余寿命,得出如下结论.

(1)当钩尾框中存在2 mm 尺寸初始裂纹(或者缺陷)时,随着裂纹形貌比的减小,伤损钩尾框的剩余寿命逐渐减小;0.8,0.5,0.3 三种形貌比裂纹的钩尾框剩余寿命分别为36,32,26 万公里,均不足一个段修期,可见2 mm 初始裂纹下车钩有安全风险.

(2)三种形貌比的裂纹扩展至12 mm 后剩余寿命均急剧下降,分别仅占总扩展寿命的4.7%,4.0%,2.2%,因此将12 mm 作为钩尾框损伤容限止裂尺寸较为合理.

(3)在裂纹形貌比0.5 的基础上减小其初始深度至0.5 mm,疲劳裂纹将处于近门槛区附近,剩余寿命约156 万公里,为2 mm 深度初始裂纹扩展寿命的4.9 倍.基于此结果可通过对危险部位进行打磨处理来降低表面粗糙度和消除微缺陷,进而显著增加服役寿命.另一方面,目前段修中对铁路货车钩尾框0.5 mm 深度裂纹的探伤极限要求可基本满足货运列车的服役安全条件.

必须指出的是,虽然通过断裂力学仿真计算得到的0.5 mm 初始裂纹的剩余寿命跨越了三个段修期,但在实际运行中情况较为复杂(材料批次、锻压工艺、装配误差、牵引功率、刹车制动、环境条件、线路条件、探伤水平等)、影响疲劳短裂纹萌生和扩展的因素众多,往往难以进行准确预测和探伤控制.如何在考虑尺寸效应的影响下,将小尺寸试样的基本力学和疲劳断裂参数修正至全尺寸构件并尽可能地准确给出安全系数将是一个重要研究课题;或者说,仅通过数值仿真方法来确定无损探伤周期并不科学,后续工作中还需要在进行大量材料试验的基础上结合基于真实服役构件的台架试验和运行数据来进行系统、全面地研究[32-33].此外,结构缺陷处应力状态与实际运行工况的差异也是影响铁路结构损伤容限设计的关键因素,本文仅考虑了钩尾框在运行中受到的拉伸载荷,在后续的工作中还应考虑由于两侧车钩中心线连挂的高度差和过曲线时产生的弯矩作用[3].