基于岩石蠕变及D-P 准则的深部巷道围岩弹塑性分析1)

经 纬 陈洪恩 杨仁树 经来旺 薛维培 王福奇

* (安徽理工大学深部煤矿采动响应与灾害防控国家重点实验室,安徽淮南 232001)

† (北京科技大学土木与资源工程学院,北京 100083)

** (华亭煤业大柳煤矿有限公司,甘肃华亭 744100)

引言

随着煤炭开采深度逐渐向深部转移,深部软岩巷道的大变形及反复维修等支护问题愈发突出[1-4].岩石的蠕变特性对深部软岩巷道围岩稳定性的影响愈发明显[5-8],且采用不同的屈服准则计算获得的围岩各变形分区应力状态与分区范围均存在明显差异.因此,考虑岩石的蠕变特性并选择合适的屈服准则进行深部软岩巷道的变形机理研究对于深部巷道支护方案的决策有着重要意义.

长期以来,国内外众多学者对围岩应变软化模型开展了大量研究,包括二阶段、三阶段和四阶段应变软化模型.许多学者基于二分区围岩应变软化模型对巷道围岩的变形特性开展了研究[9-13],然而随着煤矿开采深度的增加,二分区理论已不适用于深部巷道围岩的稳定性评估.近年来,关于围岩变形三分区的研究成果颇多,姚国圣等[14]和高召宁等[15]将围岩划分为“弹性区+塑性软化区+破裂区”三分区,考虑了岩体应变软化、扩容特性,推导出巷道围岩的应力和位移分布规律.但上述研究并未考虑围岩蠕变作用与中间主应力的影响.陈梁等[16]、潘继良等[17]和彭瑞等[18]以三阶段模型为基础,考虑了中间主应力对深部圆形巷道围岩弹塑性解析解的影响.上述研究考虑了中间主应力对巷道围岩变形规律的影响,但并未考虑围岩的蠕变影响.袁超等[19]、周建等[20]和Zou 等[21]基于蠕变提出了圆形隧道黏弹-黏塑性理论解答,但并未考虑中间主应力的作用.相关研究甚多,但均是采用未考虑岩石蠕变的3 阶段应变软化模型进行围岩变形机理的研究[22-25],因此无法准确反映深部巷道围岩变形特征.

据此,本文基于巷道围岩所能达到的最大应力应为岩石的长期强度这一特性,揭示了围岩四分区变形机理.并通过试验方法考虑了岩石的蠕变特性,计算出围岩塑性硬化区内外边界处应力值.结合中间主应力、岩体扩容及塑性软化特性,推导出围岩四分区半径、应力及位移解析解,且通过算例分析了蠕变及中间主应力等因素对围岩变形特性的影响.研究成果可为深部软岩巷道的围岩稳定性及承载力评估提供理论参考.

1 深部巷道围岩变形机理

1.1 基本假设

深部软岩巷道围岩的变形过程十分复杂,在巷道变形最终稳定之前,围岩各点应力状态始终在变化.为简化研究过程,现作如下基本假设:

(1)假设巷道为平面应变问题[26]

假设巷道围岩为均质连续介质体且各向同性,则可简化为平面应变问题进行计算;

(2)以围岩变形起始与终止状态为研究对象

以变形稳定后围岩各点径向应力对应的全应力-应变曲线作为岩石质点的加载与卸载路径.此处以变形稳定后的围岩为研究对象.

1.2 变形阶段性特征

现选取图1 所示的轴对称巷道围岩力学模型,并在围岩径向上等间隔10 个位置处选取1～10 点对巷道围岩全应力-应变曲线变化规律进行研究.依据轴对称理论,圆形巷道围岩沿径向向外各点的径向应力依次逐渐增大,环向应力则先快速增大,达到某一数值后又逐渐减小,最后两线合一,呈现出独特的规律性,如下图2 所示).围岩质点的变形路径即为特定围压下的全应力-应变曲线,由于巷道径向各点岩石应力状态不同,对应全应力-应变曲线也不同.依据材料力学中应力状态理论及相关强度理论,随着巷道围岩径向距离不断增大、径向应力不断提高,岩石的承载能力在逐渐地增强,这正是巷道围岩变形会最终停止下来的本质原因.而径向应力逐渐增大的规律则形成了巷道径向向外各岩石质点对应的全应力-应变曲线变化规律.图3 中的10 条全应力-应变曲线即为图1 中1～10 点对应的加卸载路径.由于径向向外各点处径向应力逐渐增大,故各点全应力-应变曲线如图3 所示.

图1 轴对称力学模型Fig.1 Axisymmetric mechanical model

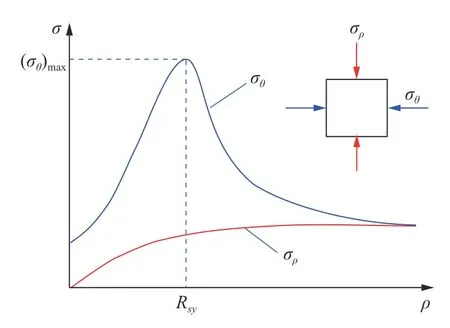
图2 巷道径向环向与径向应力变化规律Fig.2 Variation law of radial circumferential and radial stress in roadway

图3 深部巷道围岩四阶段应变软化模型Fig.3 Four-stage strain softening model of deep roadway surrounding rock

深部高应力软岩巷道围岩的一个显著特征就是蠕变.围岩中具有稳定承载能力的最大应力值实际是相应围压下的长期强度值,超过这一长期强度围岩将经历不稳定蠕变并卸压至上述长期强度以下,因此围岩应变软化模型中的峰值点对应的应力值应当是岩石的长期强度,而非以往使用的应变软化模型中的强度极限.

围岩变形阶段性特征是揭示围岩变形机理的重要环节.依据Boltman 叠加原理,围岩变形应分为两个阶段:快速加载阶段和静载蠕变阶段.

在快速加载阶段,围岩径向各岩石质点径向应力间的差异逐渐增大,并随着该阶段的结束而暂时稳定在各自对应的全应力-应变曲线的特定点处,如图3 中的点A,B,C,D,E,F,G,H,I和点K是图1 中的1～10 点在快速加载阶段完成时在各自加载路径上对应的坐标点.

图3 中,点1 对应A点正处于相应路径的残余阶段终点,表明该点已经完全破碎;点2 对应B点处于相应路径的塑性软化阶段,表明该点所处位置岩体中的裂隙相当发育但尚未完全贯通;点3 对应C点处于相应路径的峰值应力点,表明该点正在发生强度破坏;点4 对应D点处于相应路径峰前阶段的长期强度与峰值点之间位置,表明该点还将发生不稳定蠕变;点5 对应E点位于相应全应力-应变曲线的长期强度对应的应力水平上,表明该点随后将发生围岩中最大稳定蠕变;点6,7,8 和9 对应的F,G,H和I点均处于各自对应全应力-应变曲线峰前阶段的稳定蠕变上下阈值间的位置,表明这些点随后还将发生稳定蠕变;K点位于相应全应力-应变曲线弹性极限之下的某一位置,表明该点之后不会发生蠕变.A′,B′,C′,D′,E′,′F,G′,H′,I′和K′点则为静载蠕变阶段后各岩石质点在对应曲线上的位置.

2 围岩4 阶段应变软化模型

围岩应变软化模型是围岩变形稳定后围岩径向应力-应变关系曲线的理想化模型,因此该模型的建立需奠基于围岩径向不同位置处的各条应力-应变关系曲线.下面结合图3 对其残余强度阶段(破碎阶段)、塑性软化阶段、塑性硬化阶段和弹性阶段分别进行分析.

2.1 残余强度阶段

该阶段的起始点是巷道内边缘位置(图1 中点1)的应力应变坐标点(图3 中的A′点),该阶段的终止点是围岩破碎区与塑性软化区交界面位置(图1中点2)的应力应变坐标点(图3 中的B′点).显然,上述两点之间还有无数个点均处于各自对应的全应力-应变曲线的残余强度阶段,由于1 和2 两点之间的无数个点对应的全应力-应变曲线依次紧密排列且由内向外各点的环向应变值呈现依次逐渐减小的规律,同时考虑到残余强度阶段总体应变值较小,故理论上A′和B′两点之间的应力-应变关系曲线应该是一段曲率很小的曲线,通常情况下可以用直线段A′B′作为该段的理想化模型.由于围岩沿径向各点对应的全应力-应变曲线并不重合,因此围岩残余强度阶段直线段A′B′表现为一条斜直线,而并非以往应变软化模型中的水平线,如图3 所示.

2.2 塑性软化阶段

该阶段的起始点是图1 中的点2,终止点是图1中的点5,分别对应于图3 中的B′,E′两点.显然,上述两点之间还有无数个点均处于各自对应的全应力-应变曲线的塑性软化阶段,如其中的3 和4 两点在图3 中对应的C′和D′两点.与塑性流动阶段的原理相同,B′和E′两点之间的应力-应变关系曲线也应为一段曲率很小的曲线,通常可以用直线段B′E′作为该段的理想化模型.

2.3 塑性硬化阶段

该阶段的起始点是图1 中的点5,终止点是图1中的P点,两点之间还存在有无数个岩石质点,结合图3 不难看出中间的这些岩石质点均会发生稳定蠕变且稳定蠕变终止后的坐标点基本上都处于直线段NE′上或两侧近距离处,如图3 中的F′,G′,H′和I′点,通常情况下用直线段NE′作为该阶段的理想化模型.

2.4 弹性阶段

该阶段起始于图1 中的P点,终止点在径向无穷远处.由于该阶段中的所有岩石质点对应的全应力-应变曲线的下阈值点以下部位基本重合,故图3中的N点以下的任一全应力-应变曲线都可以作为围岩弹性段的应力-应变曲线,通常情况下用直线段ON作为该段的理想化模型.

综上所述,图3 中的折线ONE′B′A′就是此处要建立的四阶段围岩应变软化模型.当然,这一模型与地应力和围岩性质相关,针对某一特定的围岩,当地应力逐渐减小时,这一模型也会演化成三阶段模型或二阶段模型或一阶段模型.或针对某一特定的地应力场,当围岩强度逐渐增大时,这一模型也会从四阶段模型演化成三阶段模型或二阶段模型或1 阶段模型.此处,图3 所示的四阶段围岩终态应变软化模型实际上是一个反映各种变形分区均存在的基本模型.

塑性硬化区围岩最终将停止在稳定蠕变阶段.N点和E′点(围岩塑性硬化区外边界和内边界处)环向应力值分别为围岩弹性极限 (σθ)e(稳定蠕变下阈值)及长期强度 (σθ)∞(稳定蠕变上阈值)[27],σc为B′点(围岩破碎区外边界处)对应围岩残余强度值,σpk为围岩峰值应力;e,h,s,b 分别表示巷道围岩弹性区、塑性硬化区、塑性软化区及破碎区.

3 深部巷道围岩弹塑性分析

为了更加精准地分析深部巷道围岩的变形特性,基于上述四分区理论及中间主应力的影响,对巷道围岩的弹塑性解析解进行了分析.

3.1 力学模型

巷道力学模型如图4 所示,为简化分析现假设如下:(1)原始地应力为静水压力;(2)巷道断面呈圆形,初始地应力为两向等压均布荷载;(3)围岩为均质、连续以及各向同性的岩体.原岩应力为q,支护阻力为ps,巷道开挖半径为R0,弹性区、塑性硬化区、塑性软化区及破碎区半径分别为Re,Rh,Rs和Rb.

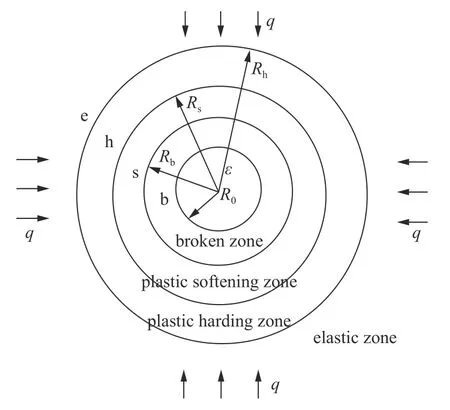
图4 巷道围岩四分区模型Fig.4 Four-zone model of surrounding rock

3.2 扩容模型

本文以四分区理论为依据,塑性软化区及破碎区围岩满足式(1)所示的岩体扩容流动法则

式中,当i表示为s 时,Δερs和 Δεθs分别表示塑性软化区岩石的径向与切向应变增量;ψs=(1+sinξ)(1-sinξ)为该区域岩体扩容参数,ξ 为膨胀角,与岩石内摩擦角 φ 近似相等[17].当i表示为b 时,和 Δεθb分别表示破碎区岩石的径向与切向应变增量;ψb=1+ω为该区域岩体扩容参数,且 0.3≤ω≤0.5[16].

3.3 黏聚力软化模型

文献[28]分析了18 项研究岩石峰后特性的成果,得出岩石破裂后内摩擦角近似不变,黏聚力明显下降,故黏聚力软化模型如图5 所示.

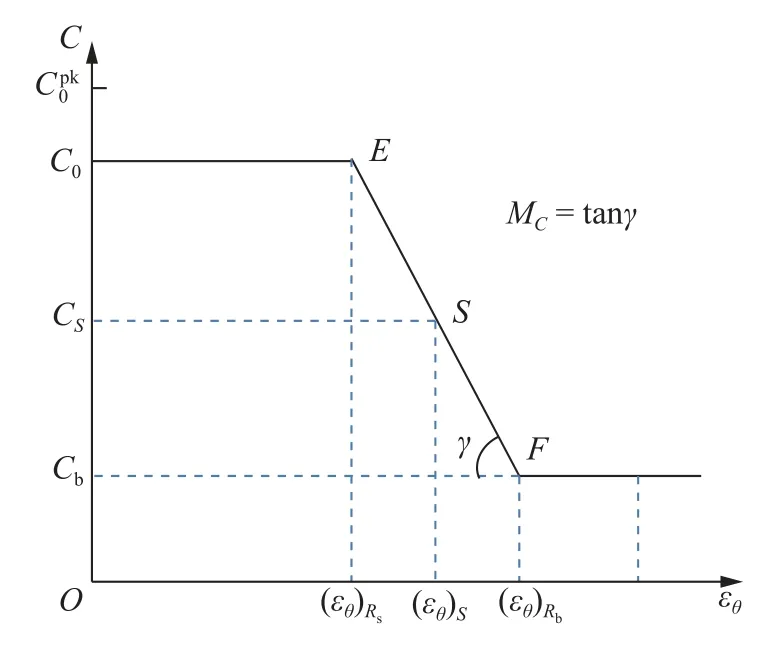
图5 考虑岩石蠕变的黏聚力软化模型Fig.5 Cohesive softening model considering creep

此处的初始黏聚力C0应以岩石长期强度拟合直线对应的单轴抗压强度值代入公式C=σc(1-sinφ)/(2cosφ)获得.塑性软化区岩石的黏聚力及软化模量可分别表示为

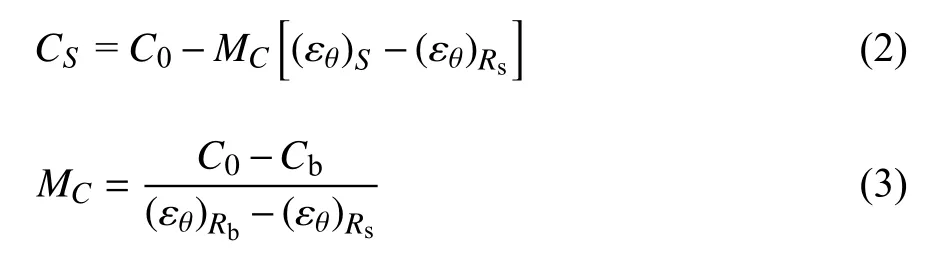
其中,Cb为残余黏聚力,CS为塑性软化区岩石黏聚力.和 (εθ)S分别为塑性软化区外边界、内边界及该区域岩石环向应变值.

由下文中理论分析得出的塑性软化区位移和应变公式(25)可得

取 ρ=Rs和Rb分别代入式(3)可得

3.4 Druck-Prager 准则

Druck-Prager (D-P)准则可考虑静水压力及中间主应力对岩石屈服特性的影响,其函数表达式为

其中,I1和J2分别为第1 应力张量不变量和第2 应力偏张量不变量,I1和J2具体公式如下

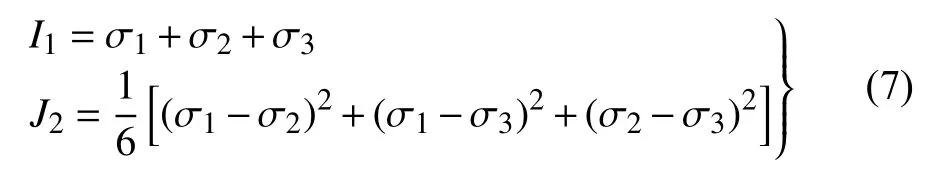
式中,λ,ζ 为D-P 准则材料参数,在平面应变关联法则下,与Mohr-Coulomb (M-C)准则中的参数围岩内摩擦角 φ 和黏聚力C之间存在如下关系[16]

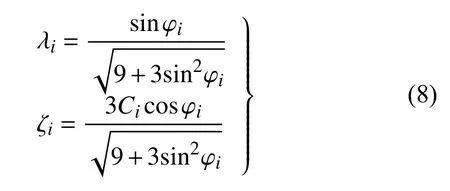
此处i指围岩分区,可表示为s 或b,分别表示塑性软化区及破碎区对应的相关参数.由上文可知,式(8)满足 φ=φs=φb,故上式可简化为

三个主应力关系可由中间主应力系数 η 表示

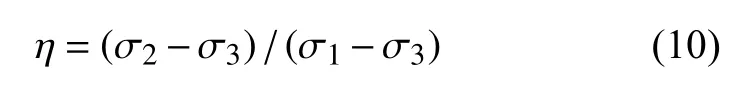
η∈[0,1],与中间主应力的影响力成正比.

联立式(10)与式(7)后代入式(6)可得

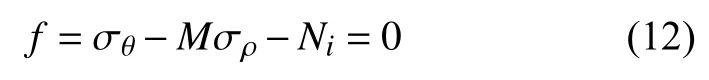
3.5 塑性硬化区边界应力的试验确定方法

为获得具体巷道围岩四分区弹塑性解答,需确定围岩塑性硬化区内外边界处径向应力值作为边界条件进行计算.相关材料蠕变本构模型无法真实考虑实际巷道围岩中不同分区岩石之间的相互作用与影响.因此,基于不同围压下岩石三轴全应力-应变试验及相同围压下设置不同轴压的三轴蠕变试验[29],通过拟合出各围压下全应力-应变曲线与相应稳定蠕变终止轨迹线的交点,即可获得此全应力-应变曲线稳定蠕变上阈值点M′点及下阈值点M点,如图6 所示.把不同围压下稳定蠕变上下阈值点分别连接起来即得到巷道围岩稳定蠕变上下阈值拟合曲线.此处将围岩径向应力 σρ作为围压 σ3,环向应力σθ作为轴压 σ1.

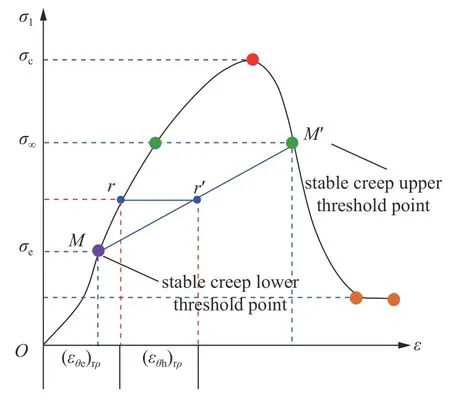
图6 塑性硬化区中某质点稳定蠕变过程Fig.6 Stable creep process of a particle in plastic hardening zone

由于围岩塑性硬化区与弹性区满足关系

式(13)对应关系直线与稳定蠕变上阈值拟合曲线交点E′的坐标值即为塑性硬化区内边界处径向应力与环向应力值;同理可得交点N对应坐标值为塑性硬化区外边界处径向应力与环向应力值,如图7 所示.

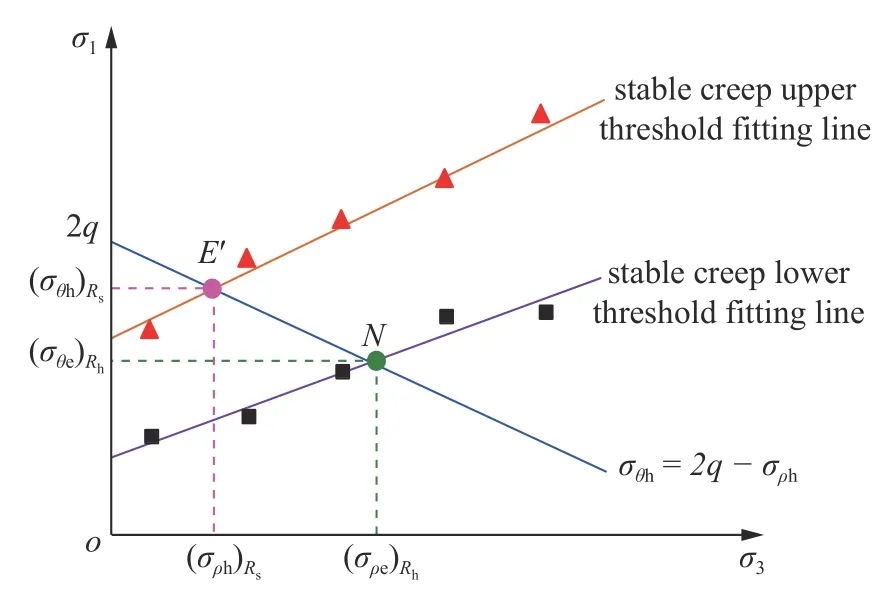
图7 围岩塑性硬化区边界应力值的试验确定方法Fig.7 Experimental determination method of boundary stress value of plastic hardening zone

此外,基于图7 所示试验方法可获得塑性硬化区内任一点处径向应力与环向应力(E′N区域内点对应坐标值),以该点径向应力值为围压进行三轴全应力-应变试验及该围压下不同轴压的三轴蠕变试验,结合图6 试验方法还可得到围岩塑性硬化区内任一点处岩石在稳定蠕变过程中的环向塑性应变值及环向总应变值.

4 围岩弹塑性应力、应变及位移解答

依据前文基本假设可得,平衡方程和几何方程分别为

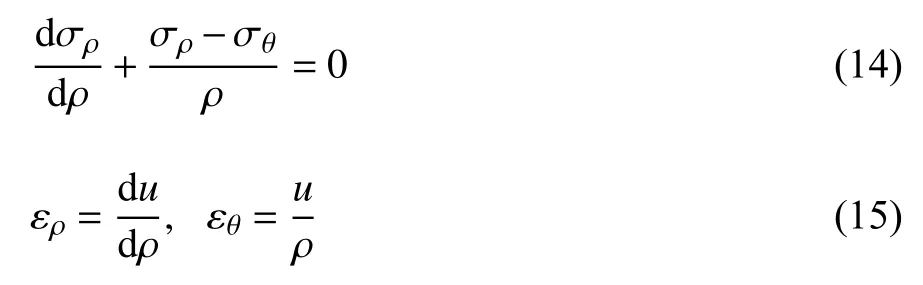
其中,ρ为任一点围岩至巷道中心的距离,u为围岩径向位移,ερ和εθ为围岩径向应变及环向应变,σρ和σθ为围岩径向应力及环向应力.

4.1 弹性区解析解

(1)弹性区围岩应力解答[26]

1.2 研究方法 超声检查由专业产科超声医师采用GE Voluson E8型彩色多普勒超声诊断仪，探头频率3～5 MHz，按照规范化标准切面，根据孕周要求测量胎儿常规项目，在11～13+6周观察胎儿NT及鼻骨，对NT异常的胎儿在11～20周加做三尖瓣血流及静脉导管血流检测。对所有胎儿进行追踪随访。

依据轴对称弹性理论,弹性区应力

(2)弹性区围岩位移及应变解答[26]

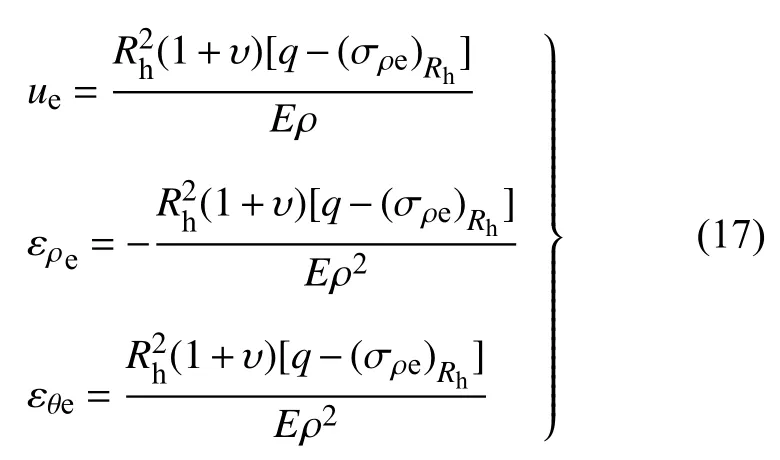
式中,E为弹性区弹性模量,为泊松比.

4.2 塑性硬化区解析解

(1)塑性硬化区围岩应力解答

由于塑性硬化区发生稳定蠕变前后应力不变,故该区域围岩应力分布规律为

(2)塑性硬化区围岩位移解答

塑性硬化区岩石可看作先发生弹性变形,然后发生稳定蠕变两个部分分别计算.

弹性径向位移计算方法与弹性区一致,为

塑性硬化区围岩的蠕变径向位移求解如下

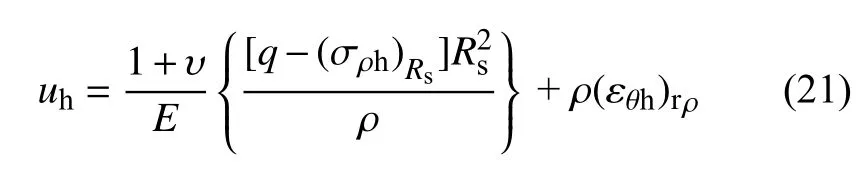
4.3 塑性软化区解析解

(1)塑性软化区应力解答

式中Ts=Ns/(1-M).

(2)塑性软化区位移与应变解答

塑性软化区内某点总应变为塑性硬化区内边界处应变和软化区内该点处塑性应变之和,故有

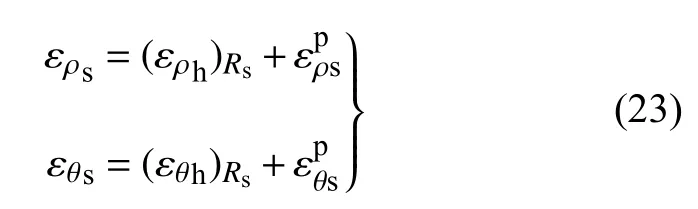
根据塑性软化区考虑岩体扩容的流动法则,联立式(1)、式(15)与式(23),并代入位移边界条件,整理后可得

4.4 破碎区解析解

(1)破碎区应力解答

联立D-P 准则式(12)与平衡方程(14),并考虑应力边界条件=ps可得

式中Tb=Nb/(1-M).

(2)破碎区位移与应变解答

假设破碎区总应变仅为塑性应变,将破碎区岩体扩容流动法则式(1)代入式(15)可得

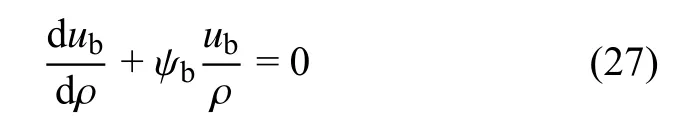
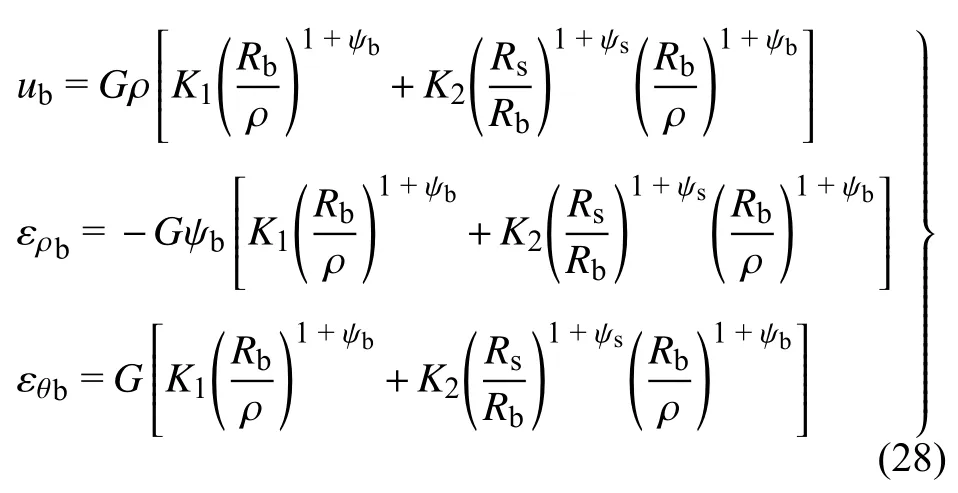
将 ρ=R0代入上式可得洞壁表面位移

4.5 巷道围岩各分区范围的确定

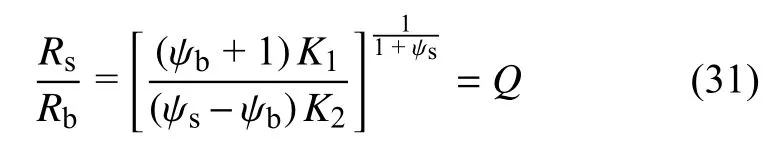
联立式(32)及式(31)可得破碎区半径公式

将上式代入式(30)及式(31),即可求出围岩所有分区半径的解析表达式.

5 工程算例验证

本文根据文献[29]中工程实例,对上述理论方法进行验证与分析,巷道尺寸如图8 所示.由于直墙拱形巷道与外接圆替代后的圆形巷道数值模拟云图十分接近[30],现取本算例中直墙拱形巷道的外接圆形成的等效圆形巷道进行计算分析.图中巷道半径和巷道宽度、高度之间存在如下关系

式中,H 与 LOC分别为巷道高度和1/2 巷道宽度,将图8 中的数据代入上式,即可获得圆形断面的半径值R0=2.95 m.

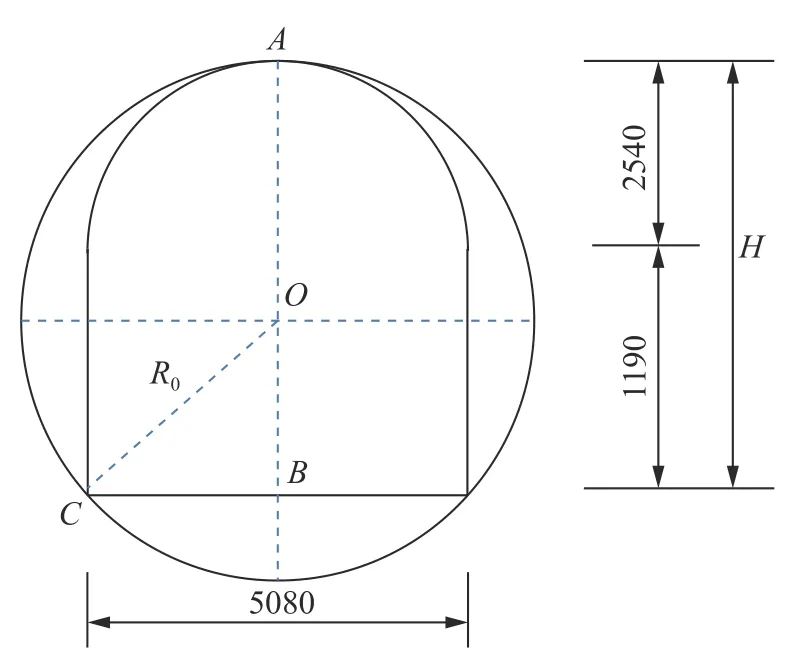
图8 等效圆形巷道断面示意图 (单位:mm)Fig.8 Section diagram of equivalent circular roadway (unit:mm)

故现取巷道开挖等效半径R0=2.95 m,初始地应力q=21.861 MPa,巷道围岩最大主应力为20.42 MPa,最小主应力为9.49 MPa,中间主应力为17.55 MPa,故中间主应力系数近似为0.7.围岩弹性模量E=4.01 GPa,泊松比 υ=0.25,内摩擦角 φ=27.83°,支护荷载为ps=0.75 MPa.围岩瞬时极限强度对应的C0==11.57 MPa,围岩长期强度对应的C0==5.578 MPa,残余黏聚力Cb=0.724 MPa.

应用本文理论计算可得到D-P 模型(考虑蠕变)对应的围岩各分区半径值如表1 所示.故帮部和顶部破碎区范围分别为:帮部=5.677-2.540 (巷宽)=3.137 m;顶部=5.677-2.950 (巷道半径)=2.727 m.为验证上述理论的科学性,本人结合不同力学模型理论解答,计算出不考虑蠕变的三分区M-C 模型(C0=)[14],考虑蠕变的四分区M-C 模型(C0=)[29]和本文考虑蠕变的四分区D-P 模型三种情况下的围岩各分区半径值,并采用徐州产YDSG-10 型岩层钻孔窥视仪完成现场观测,与三种计算数值进行对比.监测断面共设置7 个观测钻孔点,钻孔设计深度均为3 米,钻孔窥视孔图像见图9,钻孔布置图如图10所示.

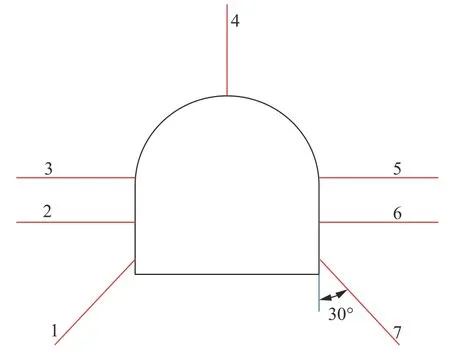
图10 松动圈测试钻孔布置图Fig.10 Loose circle test drilling plan

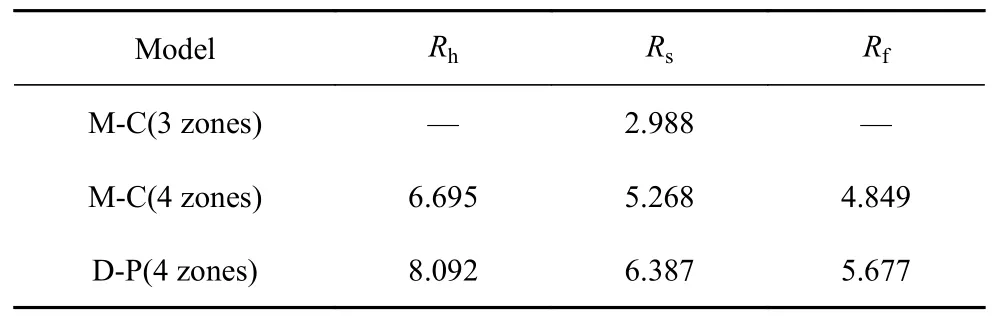
表1 不同力学模型下的分区半径对比Table 1 Comparison of partition radii under different models

为了与上文D-P 模型(考虑蠕变)对应的巷道帮部和顶部破碎区计算范围进行对比验证,现对2,3,4,5 和6 号观测孔读取数据进行分析.根据图9,2 号窥视孔至0.5 m 处均为较严重破碎带,0.5～1.0 米之间岩体存在裂隙,受岩体泥浆影响该孔仅能观测至1.2 m 处.3 号窥视孔至3.0 m 处岩体依然呈破碎状态.4 号窥视孔2.5 m 内为明显松动破碎岩体,2.8 m 处岩体基本完好.5 号窥视孔0.8 m 处存在严重破碎脱落现象,1.7～2.7 m 可见破碎状态,超过2.7 m 岩体基本完好.6 号窥视孔在1.0 m 和1.5 m处均出现破碎脱落区,2.8 m 处也发现破碎现象但并不明显.

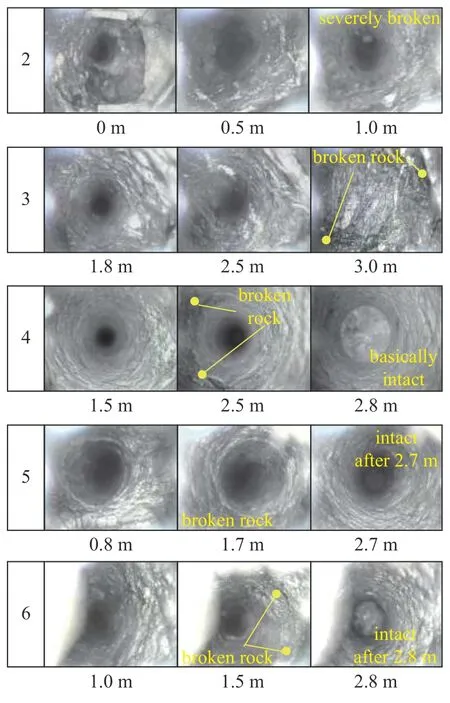
图9 观测钻孔处窥视孔图像Fig.9 Peephole image of observation hole

观测结果表明:巷道围岩破碎区范围平均在2.2～3.0 m.帮部部位破碎区范围较大,3 号孔超过3.0 m,5 号孔达到2.7 m 附近,6 号孔达到2.8 m 左右,故平均值约在3 m 左右;顶部破碎区较小,约在2.5～2.8 m.据此可知,窥视孔测试结果与本文理论计算结果基本吻合,从而论证了本文理论的可靠性.此外由表1 可知,M-C 模型(不考虑蠕变)[14]对应半径解无破碎区,与事实不符;M-C 模型(考虑蠕变)[29]获得的帮部和顶部破碎区范围分别为帮部2.309 m,顶部1.899 m,与实测数据相比明显偏小.综上所述,本文方法较其他两种方法更为精准,而M-C模型计算结果更为保守.

6 影响因素敏感度分析

由上文可知,围岩蠕变对深部巷道围岩各变形分区范围有着重要影响.而实际围岩的最大应力值应为长期强度这一特性直接表现为初始黏聚力C0数值的选取不同.同时,诸多文献表明中间主应力对围岩变形的影响同样不容忽视[17-19].因此,为进一步分析蠕变及中间主应力对围岩变形分区的影响,下面逐一分析初始黏聚力C0、中间主应力系数η、黏聚力软化模量MC及内摩擦角 φ 对巷道围岩各分区范围及洞壁位移的影响.

6.1 初始黏聚力与中间主应力对巷道围岩各分区半径及洞壁位移的影响

通过联立式(5)、式(30)及式(33)可获得关于C0和MC的围岩各分区半径解答,并得到C0与 η 对分区半径及洞壁位移的影响规律,如图11 所示.随C0增大,各分区半径均呈不同程度减小,且减小速率逐步增大;塑性硬化区半径减小速率最快,塑性软化区半径减小速率最慢.依据图12,当 0≤η≤0.7 时,围岩各分区半径均随 η 值增大而减小;当0.7≤η≤1时,各分区半径均随 η 值增大而增大.η 从0 增加至0.7 时,当C0=3 MPa,各分区范围缩小速率:Rh(10.478)＞Rs(8.109)＞Rb(7.624);当C0=6 MPa,缩小速率为:Rh(4.506)＞Rs(3.556)＞Rb(3.135).故各分区范围缩小速率有:Rh＞Rs＞Rb;且在同等 η 值区间内,随C0增大各分区半径缩小速率明显减小.

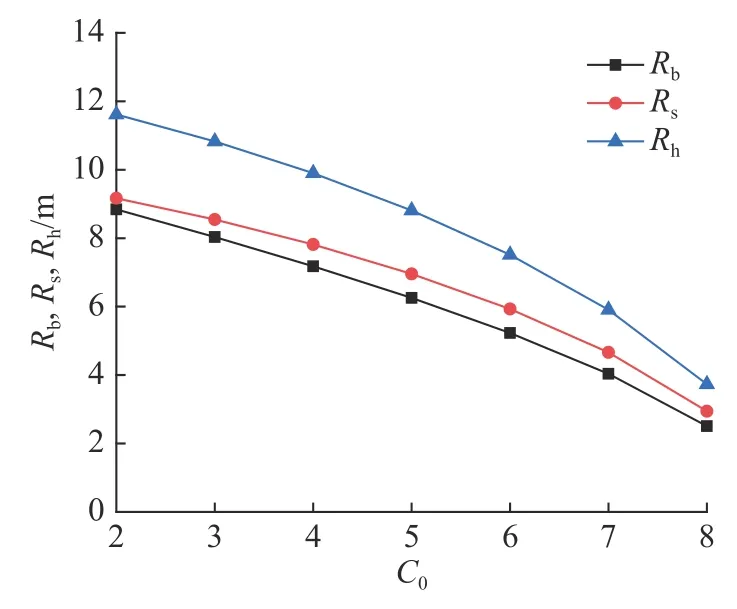
图11 C0 对巷道围岩各分区半径的影响Fig.11 Effect of C0 on zoning radius of surrounding rock

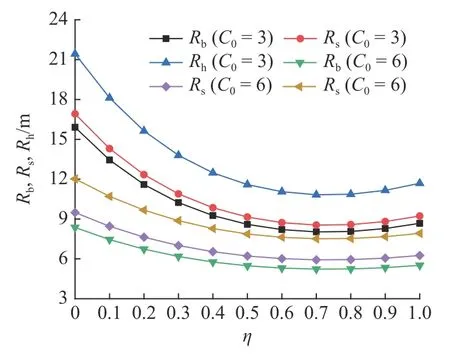
图12 η 及C0 对围岩各分区半径的影响Fig.12 Effect of zoning radius of surrounding rock with η and C0

综上所述,忽略围岩蠕变影响时,C0取值将明显大于实际值,使得围岩各分区半径计算值较实际值偏小,导致围岩理论承载能力大于实际承载能力,对支护设计不利;随着C0的增大,η 取值对各分区范围影响力不断减弱,η =0.7 时,Rh,Rb及Rs均取得最小值,且当 η 处于[0,0.7]区间内时,提高 η 值则可有效控制围岩各变形分区塑性区及破碎区范围的拓展,从而提高围岩稳定性.

图13 为洞壁位移u0随中间主应力 η 及初始黏聚力C0的变化规律曲线.当 0≤η≤0.7时,随 η 增大,巷道洞壁位移量不断减小,且C0越小,洞壁位移减小速率越快;当 0.7≤η≤1时,随 η 增大,巷道洞壁位移量逐渐增大.同时,当 η 值一定时,C0越大,洞壁位移量越小.结果表明:η =0.7 处为巷道洞壁位移量最小处;随C0减小,巷道变形量不断增大,且巷道表面位移量对 η 数值的敏感度不断升高.由此可见,考虑围岩蠕变特性时,C0将明显减小,中间主应力系数对巷道变形实际影响力显著提高,且巷道洞壁变形量将明显变大.

图13 η 及C0 对洞壁位移的影响Fig.13 Effect of η and C0 on wall displacement

6.2 内摩擦角与中间主应力对围岩半径的影响

图14 为内摩擦角与中间主应力对围岩各分区半径的影响规律曲线.由图可知,当中间主应力系数一定,φ=28o时各分区半径均小于 φ=24o时半径值.随内摩擦角增大,围岩各分区半径变化速率将会减小.当内摩擦角一定时,随着 η 增大,各分区半径变化速率基本一致,具体以 η=0.7 为分界点,先减小后增大.结果表明:岩石内摩擦角越大,围岩塑性硬化区、塑性软化区及破碎区范围越小;内摩擦角越大,中间主应力系数对围岩塑性区及破碎区范围影响力将不断减弱.

图14 围岩各分区半径随φ 与η 的变化规律Fig.14 Variation of zoning radius of surrounding rock with φ and η

6.3 黏聚力软化模量与初始黏聚力对巷道围岩各分区半径的影响

图15 表示围岩各分区半径随MC与C0的变化规律.由图可知,随着MC的增大,各分区半径呈逐渐增大趋势,且增大速率不断减小;塑性软化区和破碎区半径变化速率基本相同,塑性硬化区半径增长速率明显快于另两个分区半径.当MC一定时,C0越大,各分区半径随MC变化速率越快.因此,MC增大时,围岩塑性区及破碎区范围将向外扩展,且塑性硬化区及破碎区范围将明显增大;同时,随着C0的减小,MC对围岩各分区范围的影响力不断减弱.因此,忽视围岩蠕变特性将高估MC对塑性区及破碎区范围的影响.

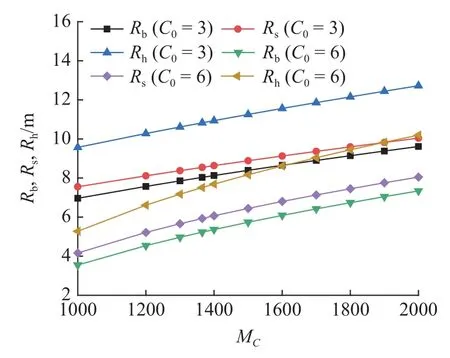
图15 分区半径随MC 与C0 变化规律Fig.15 Variation of zoning radius of surrounding rock with MC and C0

7 结论

(1)提出了一种只考虑围岩蠕变的起始与终止状态,而忽略复杂多变的蠕变中间过程的新型研究方法,并通过剖析长期荷载作用下的巷道围岩变形特征,揭示了四分区巷道围岩变形机理.

(2)考虑了中间主应力、应变软化与岩体扩容特性,推导出巷道围岩的应力、变形以及各分区半径的理论解答.结合工程算例将本文求解结果与现场实测及不同屈服准则情况下理论解析解进行对比,验证了本文方法的科学性及可靠性.

(3)揭示了考虑围岩蠕变特性、中间主应力、黏聚力软化模量及内摩擦角对围岩塑性区、破碎区及巷道变形的影响规律.忽视围岩蠕变作用将高估围岩的自承载能力;中间主应力对巷道围岩变形及塑性区、破碎区扩展表现出明显的区间性;初始黏聚力及内摩擦角减小,将导致中间主应力系数对围岩塑性区、破碎区范围及巷道变形的影响力显著提高;考虑围岩蠕变作用时,黏聚力软化模量对塑性区及破碎区范围的影响力将减弱.